为什么verilog中递归函数需要定义为automatic?
直接上代码
module automatic_tb;reg [7:0] value;initial begin #0 value <= 8'd5;#10 $display("result of automatic: %0d", factor_automatic(value));$display("result of static: %0d", factor_static(value));#50 $stop;
endfunction reg[7:0] factor_static (input reg[7:0] dat);if (dat >= 2) beginfactor_static = factor_static(dat-1) * dat;endelsefactor_static = 1;
endfunctionfunction automatic reg[7:0] factor_automatic (input reg[7:0] dat);if (dat >= 2) beginfactor_automatic = factor_automatic(dat-1) * dat;endelsefactor_automatic = 1;
endfunctionendmodule
得到的仿真结果为:
 从上述的仿真结果中可以看到,此时automatic的函数对应的结果是对的,而static的函数对应的结果是错误的。
从上述的仿真结果中可以看到,此时automatic的函数对应的结果是对的,而static的函数对应的结果是错误的。
原因分析
对于static函数而言,此函数中对应的变量都是static,也就是只存在一份。以上述的列子为例,当factor_static递归四次的时候,此时dat的值为1,即这唯一的一份dat的值为1,并且此时result也被置为1,当函数进行到上一层的时候,此时factor_static(2)的值为1,而dat的也是1,所以当前这一次返回的值也为1,因此最终的结果为1。具体的流程见下图:

在国外的网站上看到的另一个分析static和automatic函数的例子
module static_tb;task add(input reg[7:0] a, input reg[7:0] b);
begin#2;$display("the sum is %0d", a+b);
end
endtaskinitial
forkbegin add(2, 3);endbegin#1;add(3, 4);end
join endmodule

可以看到,这里的两个sum输入的参数不同,但是得到的结果却是相同的。这是由于在time为0的时候,add(2, 3)进行执行,将a设置为2,b设置为3,然后等待2个时间单位准备输出,但是在经过了1个时间单位之后,add(3,4)进行执行,又将a设置为3,b设置为4,所以再又经过一个时间单位之后,输出的结果为7,从而看到的结果都是7。
此案例的参考地址
相关文章:

为什么verilog中递归函数需要定义为automatic?
直接上代码 module automatic_tb;reg [7:0] value;initial begin #0 value < 8d5;#10 $display("result of automatic: %0d", factor_automatic(value));$display("result of static: %0d", factor_static(value));#50 $stop; endfunction reg[7:0] fa…...

23种设计模式-状态(State)设计模式
文章目录 一.什么是状态模式?二.状态模式的结构三.状态模式的应用场景四.状态模式的优缺点五.状态模式的C实现六.状态模式的JAVA实现七.代码解释八.总结 类图: 状态设计模式类图 一.什么是状态模式? 状态模式(State Pattern&…...

EventListener与EventBus
EventListener JDK JDK1.1开始就提供EventListener,一个标记接口,源码如下: /*** A tagging interface that all event listener interfaces must extend.*/ public interface EventListener { }JDK提供的java.util.EventObject࿱…...

Facebook为什么注册失败了?该怎么解决?
有时候用户在尝试注册Facebook账号时可能会遇到各种问题,导致注册失败或遇到困难。小编会为大家分析Facebook注册失败的可能原因,并提供解决方法,帮助大家顺利完成注册流程。 一、Facebook注册失败的可能原因 1. 账号信息问题: …...

前端数据可视化思路及实现案例
目录 一、前端数据可视化思路 (一)明确数据与目标 (二)选择合适的可视化图表类型 (三)数据与图表的绑定及交互设计 (四)页面布局与样式设计 二、具体案例:使用 Ech…...
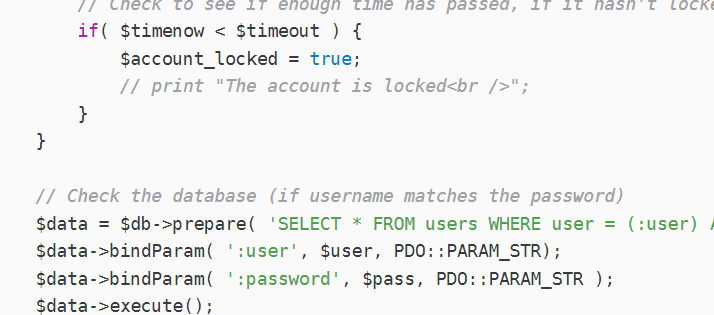
【DVWA】Brute Force暴力破解实战
问尔辈 何等样人 自摸心头 再来求我;若汝能 克存忠孝 持身正直 不拜何妨 1.Brute Force(Low) 相关的代码分析 if( isset( $_GET[ Login ] ) ) {// Get username$user $_GET[ username ];// Check the database$query "SELECT * FROM users WHERE user $…...

23种设计模式速记法
前言 在软件开发的过程中,设计模式作为解决常见问题的通用模板,一直是开发者的重要工具。尤其是在面临复杂系统架构和需求变化时,设计模式不仅能够提升代码的可复用性和扩展性,还能大大提高团队之间的协作效率。然而,…...

第7章硬件测试-7.3 功能测试
7.3 功能测试 7.3.1 整机规格测试7.3.2 整机试装测试7.3.3 DFX测试 功能测试包括整机规格、整机试装和整机功能测试,是整机结构和业务相关的测试。 7.3.1 整机规格测试 整机规格测试包括尺寸、重量、温度、功耗等数据。这些测试数据与设计规格进行比对和校验&…...

动态规划子数组系列一>等差数列划分
题目: 解析: 代码: public int numberOfArithmeticSlices(int[] nums) {int n nums.length;int[] dp new int[n];int ret 0;for(int i 2; i < n; i){dp[i] nums[i] - nums[i-1] nums[i-1] - nums[i-2] ? dp[i-1]1 : 0;ret dp[i…...

《Python浪漫的烟花表白特效》
一、背景介绍 烟花象征着浪漫与激情,将它与表白结合在一起,会创造出别具一格的惊喜效果。使用Python的turtle模块,我们可以轻松绘制出动态的烟花特效,再配合文字表白,打造一段专属的浪漫体验。 接下来,让…...

什么是RESTful API,有什么特点
RESTful API 概述 什么是 RESTful API? RESTful API 是基于 Representational State Transfer(表现层状态转移)架构风格的 Web 服务接口。REST 是一种设计风格,而不是具体的协议或标准。它定义了一组约束和最佳实践,…...
友思特新闻 | 友思特荣获广州科技创新创业大赛智能装备行业赛初创组优胜企业!
2024年11月19日,第十三届中国创新创业大赛(广东广州赛区)暨2024年广州科技创新创业大赛智能装备行业赛颁奖典礼隆重举行。 赛事奖项介绍:广州科技创新创业大赛智能装备行业赛 第十三届“中国创新创业大赛(广东广州赛区…...

CSS中calc语法不生效
问题起因 在使用calc时发现无法生效,写法是: height:calc(100vh-100px);页面无效果,加空格后就发现有效果了: height:calc(100vh - 100px);这是为什么? calc是什么? css3 的计算属性,用于动态…...

国标GB28181视频平台EasyCVR视频融合平台H.265/H.264转码业务流程
在当今数字化、网络化的视频监控领域,大中型项目对于视频监控管理平台的需求日益增长,特别是在跨区域、多设备、高并发的复杂环境中。EasyCVR视频监控汇聚管理平台正是为了满足这些需求而设计的,它不仅提供了全面的管理功能,还支持…...

ES6 模板字符串详解
ES6 模板字符串详解 ES6(ECMAScript 6)引入了模板字符串(Template Literals),这是一种新的字符串字面量语法,使用反引号()来定义字符串。模板字符串不仅支持多行字符串,…...

浏览器插件启动本地程序
浏览器插件支持启动本地程序,且支持win、mac、linux多个平台,使用的是nativeMessaging。nativeMessaging官方api说明。nativeMessaging支持启动本地程序且进行通信。 我们直接拿官方提供的例子进行说明,github地址。 以win为例 1、添加注册…...

Ubuntu ESP32开发环境搭建
文章目录 ESP32开发环境搭建安装ESP-IDF搭建一个最小工程现象 ESP32开发环境搭建 最近有个小项目需要用到能够联网的mcu驱动,准备玩玩esp的芯片,记录下ESP32开发环境搭建的过程。 ESP-IDF 是乐鑫科技为其 ESP32 系列芯片提供的官方开发框架。这个框架主…...

【gitlab】部署
直接RPM安装 部署的方式是:使用外部的nginx作为代理,使用https方式。 1、下载安装文件 gitlab-ce-17.0.3-ce.0.el7.x86_64.rpm 2、安装 yum install gitlab-ce-17.0.3-ce.0.el7.x86_64.rpm 或者安装yum源在线安装: 添加镜像源:新建 /et…...

vue中路由缓存
vue中路由缓存 问题描述及截图解决思路关键代码及打印信息截图 问题描述及截图 在使用某一平台时发现当列表页码切换后点击某一卡片进入详情页后,再返回列表页时页面刷新了。这样用户每次看完详情回到列表页都得再重新输入自己的查询条件,或者切换分页到…...

Github 2024-11-18 开源项目周报 Top15
根据Github Trendings的统计,本周(2024-11-18统计)共有15个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Python项目8TypeScript项目4Jupyter Notebook项目2Go项目2Shell项目1OpenHands: 人工智能驱动的软件开发代理平台 创建周期:195 天开发语言:P…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
