线段数--算法

线段树是常用来维护 区间信息 的数据结构

线段树可以在 O(logN) 的时间复杂度内实现

• 单点修改
• 区间修改
• 区间查询

• • 区间求和
  • 求区间最大值
  • 求区间最小值

简单介绍一下线段树

线段树是一个将区间内的数不断细分的一种数据结构，也就是一个完全二叉树，用每一个叶子节点代表一个区间内的值

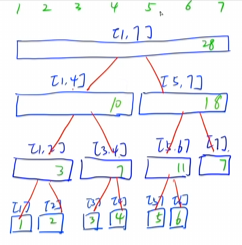
操作1：单点修改

单点修改是找到要修改的那个点所在的每一层的区间，最后通过叶子节点，修改为相应的值，然后向上递归

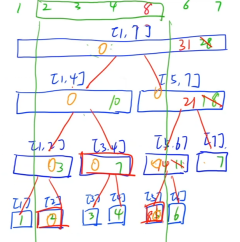
操作2：区间查询

区间查询[l,r]是指在线段树内从上向下查询，如果子区间的左右端点都在[l,r]内则不用在向下递归，直到找到所有的点

常用操作函数

1. pushup(int u)：用子节点的信息更新当前节点

1. 1. 参数u是根节点

static void pushUp(int u){node[u].sum=node[u<<1].sum+node[u<<1|1].sum;
}

1. build(int u,int l,int r)：在一段区间上初始化线段树

1. 1. 参数u是根节点，l是区间左端点，r是区间右端点

static void build(int u,int l,int r){if(l==r)node[u]=new Node(l,r,w[r]);else{node[u]=new Node(l,r,0);int mid=l+r>>1;build(u<<1,l,mid);build(u<<1|1,mid+1,r);pushUp(u);}
}

1. modify(int u,int x,int v)：修改某一点的值

1. 1. 参数u是根节点，x是要修改的节点，v是要增加或减小的值

static void modify(int u,int x,int v){if(node[u].l==node[u].r)node[u].sum+=v;else{int mid=(node[u].l+node[u].r)>>1;if(x<=mid)modify(u<<1,x,v);else modify(u<<1|1,x,v);pushUp(u);}
}

1. query(int u,int l,int r)：查询

1. 1. 参数u是根节点，l是区间左端点，r是区间右端点

static int query(int u,int l,int r){if(node[u].l>=l&&node[u].r<=r)return node[u].sum;int mid=node[u].l+node[u].r>>1;int sum=0;if(l<=mid)sum+=query(u<<1,l,r);if(r>mid)sum+=query(u<<1|1,l,r);return sum;
}

节点表示

父节点：x/2 ==> x>>1

左儿子：2x ==> x<<1

右儿子：2x+1 ==> x>>1|1

---

动态求连续区间和

package 线段树;import java.io.BufferedReader;
import java.io.InputStreamReader;public class Main {static int N=1000010;static Node[] node=new Node[N];static int[] w=new int[N];static BufferedReader br=new BufferedReader(new InputStreamReader(System.in));static int n,m;static String[] $;static void pushUp(int u){node[u].sum=node[u<<1].sum+node[u<<1|1].sum;}static void build(int u,int l,int r){if(l==r)node[u]=new Node(l,r,w[r]);else{node[u]=new Node(l,r,0);int mid=l+r>>1;build(u<<1,l,mid);build(u<<1|1,mid+1,r);pushUp(u);}}static int query(int u,int l,int r){if(node[u].l>=l&&node[u].r<=r)return node[u].sum;int mid=node[u].l+node[u].r>>1;int sum=0;if(l<=mid)sum+=query(u<<1,l,r);if(r>mid)sum+=query(u<<1|1,l,r);return sum;}static void modify(int u,int x,int v){if(node[u].l==node[u].r)node[u].sum+=v;else{int mid=(node[u].l+node[u].r)>>1;if(x<=mid)modify(u<<1,x,v);else modify(u<<1|1,x,v);pushUp(u);}}public static void main(String[] args)throws Exception {$=br.readLine().split(" ");n=Integer.parseInt($[0]);m=Integer.parseInt($[1]);$=br.readLine().split(" ");for(int i=1;i<=n;i++)w[i]=Integer.parseInt($[i-1]);build(1,1,n);while (m-->0){$=br.readLine().split(" ");int k=Integer.parseInt($[0]);int a=Integer.parseInt($[1]);int b=Integer.parseInt($[2]);if(k==0)System.out.println(query(1,a,b));else modify(1,a,b);}}
}class Node{int l,r,sum;public Node(int l,int r,int sum){this.l=l;this.r=r;this.sum=sum;}
}