VB、VBS、VBA的区别及作用
VB、VBS 和 VBA 是三种与微软 Visual Basic 相关的编程语言或环境,它们在功能和用途上有所不同:
# Visual Basic (VB)
Visual Basic 是一种面向对象的编程语言,最初由微软公司开发。它是一种高级编程语言,旨在简化开发过程,使非专业程序员也能快速上手。
VB 语言提供了丰富的控件和事件驱动的编程模型,使得开发图形用户界面(GUI)应用程序变得容易。
Visual Basic 的早期版本(如 VB 6.0)是独立的开发环境,而后来的版本(如 VB.NET)被集成到了 Visual Studio 中。
# Visual Basic Scripting Edition (VBScript)
VBScript 是一种轻量级的、解释型的脚本语言,它是微软对 ECMAScript(JavaScript 的一个标准)的一个实现。
VBScript 通常用于网页(客户端脚本)和 Windows 脚本宿主(如 Windows 脚本宿主,WSH)来自动化 Windows 任务。
它是一种非常简化的 VB 版本,主要用于编写简单的脚本,而不是完整的应用程序。
VBScript 已经不再是现代 Web 开发的首选语言,因为它在安全性和功能上都有所限制。
# Visual Basic for Applications (VBA)
VBA 是一种事件驱动的编程语言,它是 Visual Basic 的一个子集,专门设计用于 Microsoft Office 应用程序的自动化。
VBA 允许用户自定义和扩展 Office 应用程序的功能,如 Excel、Word、Access 等。
通过 VBA,用户可以创建宏来自动化重复性任务,开发自定义的解决方案,以及创建复杂的数据处理和分析工具。
VBA 通常嵌入在 Office 文档中,如 Excel 电子表格或 Word 文档,使得用户可以在 Office 应用程序内部编写和运行代码。
# 总结
1.VB 是一种完整的编程语言,用于开发桌面应用程序;
2.VBScript 是一种脚本语言,用于网页和自动化 Windows 任务;
3.VBA 是一种专门为 Microsoft Office 应用程序设计的编程语言,用于自动化和扩展这些应用程序的功能。
4.随着技术的发展,VB 和 VBScript 的使用已经大大减少,而 VBA 仍然是许多企业和个人用户在 Office 应用程序中进行自动化的首选工具。
相关文章:

VB、VBS、VBA的区别及作用
VB、VBS 和 VBA 是三种与微软 Visual Basic 相关的编程语言或环境,它们在功能和用途上有所不同: # Visual Basic (VB) Visual Basic 是一种面向对象的编程语言,最初由微软公司开发。它是一种高级编程语言,旨在简化开发过程&…...
与时间序列预测)
深度学习中的循环神经网络(RNN)与时间序列预测
一、循环神经网络(RNN)简介 循环神经网络(Recurrent Neural Networks,简称RNN)是一种专门用于处理序列数据的神经网络架构。与传统神经网络不同,RNN具有内部记忆能力,能够捕捉数据中的时间依赖…...
详解)
Unity 设计模式-原型模式(Prototype Pattern)详解
原型模式 (Prototype Pattern) 原型模式 (Prototype Pattern) 是一种创建型设计模式,它允许通过复制现有的对象来创建新对象,而不是通过直接实例化类。这意味着你可以通过克隆原型对象来生成新的实例,而不必依赖类的构造函数。该模式的核心思…...

如何在 RK3568 Android 11 系统上排查以太网问题
1. 硬件连接检查 在进行软件诊断之前,首先确保所有硬件连接正常: 确认网线可靠插入设备的以太网端口。交换机、路由器中与设备连接的端口是否正常工作。若有可能,尝试更换网线或使用其他端口。2. 使用命令行工具进行基本检查 检查网络接口状态 连接设备并使用 ADB 或终端…...
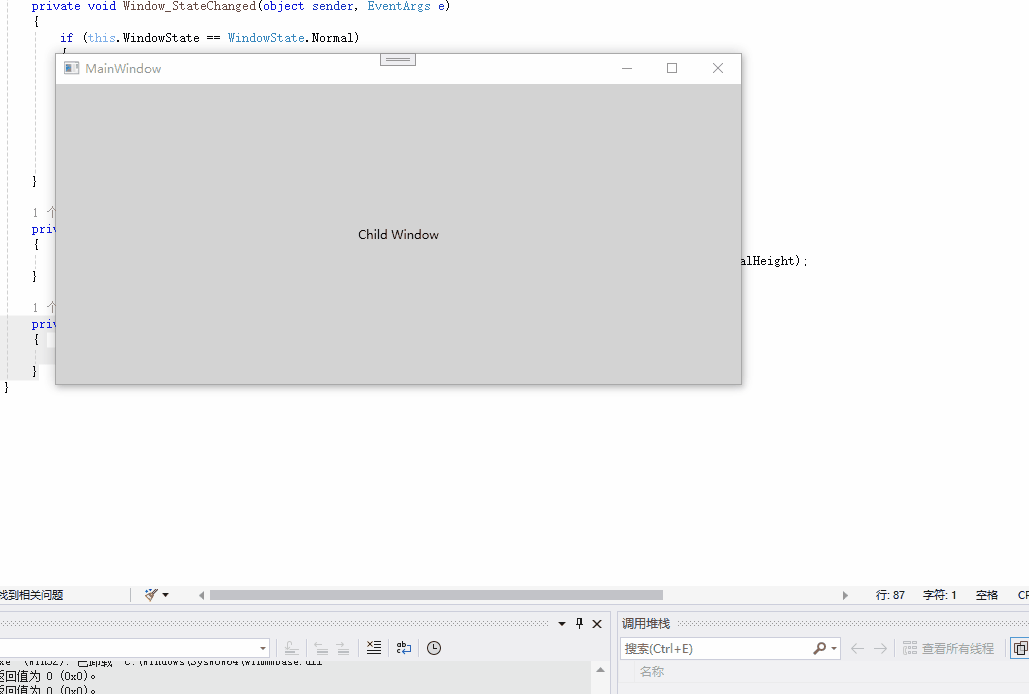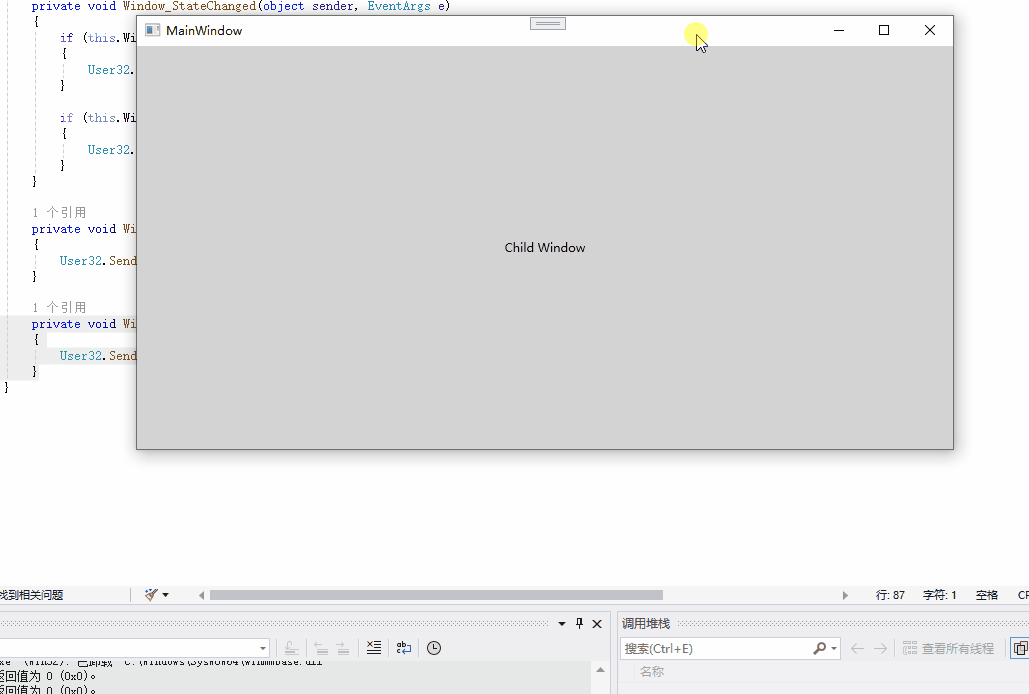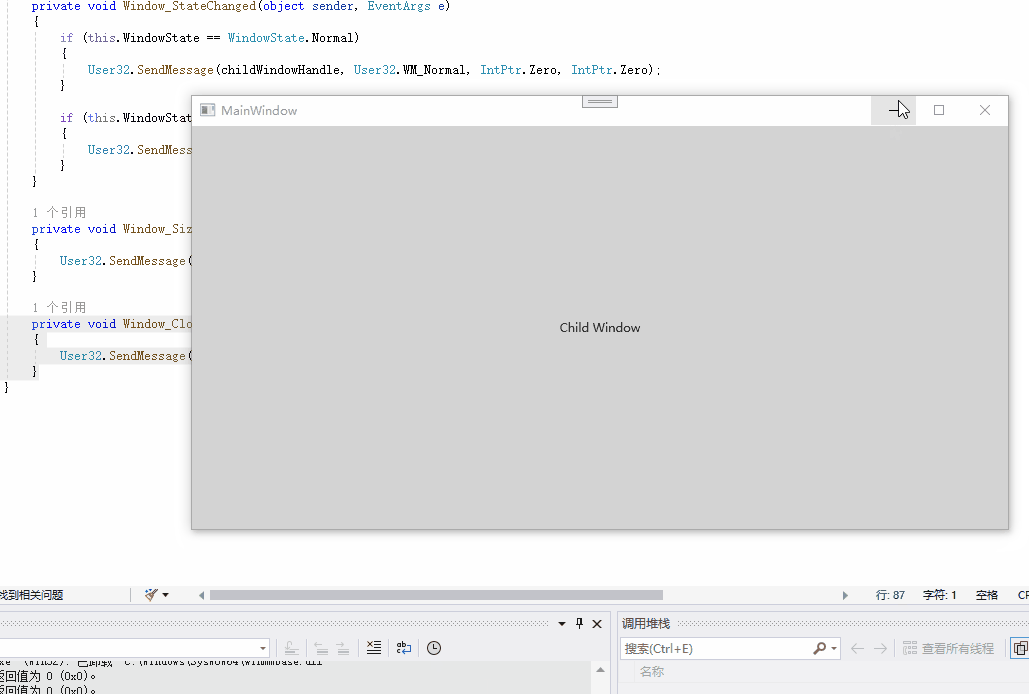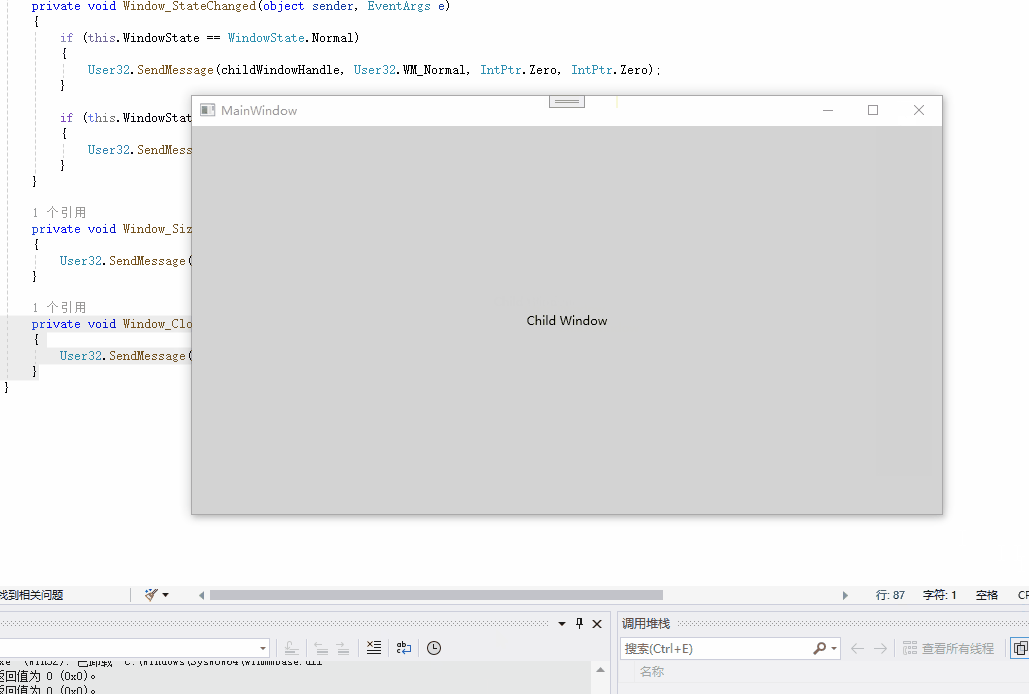
如何在WPF中嵌入其它程序
在WPF中嵌入其它程序,这里提供两种方案 一、使用WindowsFormHost 使用步骤如下 1、添加WindowsFormsIntegration和System.Windows.Forms引用 2、在界面上放置WindowsFormHost和System.Windows.Forms.Panel 1 <Grid> 2 <WindowsFormsHost> 3…...

大模型呼入系统是什么?
大模型呼入系统是什么? 作者:开源呼叫中心系统 FreeIPCC,Github地址:https://github.com/lihaiya/freeipcc 在呼叫中心领域,大模型呼入是指利用大型语言模型(如GPT等)处理客户呼入的电话请求&a…...

Flutter:SlideTransition位移动画,Interval动画延迟
配置vsync,需要实现一下with SingleTickerProviderStateMixinclass _MyHomePageState extends State<MyHomePage> with SingleTickerProviderStateMixin{// 定义 AnimationControllerlate AnimationController _controller;overridevoid initState() {super.…...

【Elasticsearch入门到落地】2、正向索引和倒排索引
接上篇《1、初识Elasticsearch》 上一篇我们学习了什么是Elasticsearch,以及Elastic stack(ELK)技术栈介绍。本篇我们来什么是正向索引和倒排索引,这是了解Elasticsearch底层架构的核心。 上一篇我们学习到,Elasticsearch的底层是由Lucene实…...

网络安全概论
一、 网络安全是一个综合性的技术。在Internet这样的环境中,其本身的目的就是为了提供一种开放式的交互环境,但是为了保护一些秘密信息,网络安全成为了在开放网络环境中必要的技术之一。网络安全技术是随着网络技术的进步逐步发展的。 网络安…...

后端开发如何高效使用 Apifox?
对于后端开发者来说,日常工作中少不了接口的设计、调试和文档编写。你是否也曾因接口文档更新不及时、测试工具分散而头疼不已?Apifox,这款全能型工具,或许能成为你的效率神器! Apifox究竟有哪些功能能帮助后端开发者…...

实现List接口的三类-ArrayList -Vector -LinkedList
一、ArrayList 数据结构与存储原理 ArrayList是基于动态数组实现的。它在内存中是一块连续的存储空间。当创建一个ArrayList时,会初始化一个默认大小(通常为10)的数组。随着元素的不断添加,如果数组容量不够,会进行扩…...

LeetCode 904.水果成篮
LeetCode 904.水果成篮 思路🧐: 求水果的最大数目,也就是求最大长度,我们是单调的向前求解,则能够想到使用滑动窗口进行解答,可以用hash表统计每个种类的个数,kinds变量统计当前种类,…...
GitHub 开源项目 Puter :云端互联操作系统
每天面对着各种云盘和在线应用,我们常常会遇到这样的困扰。 文件分散在不同平台很难统一管理,付费订阅的软件越来越多,更不用说那些烦人的存储空间限制了。 最近在 GitHub 上发现的一个开源项目 Puter 彻底改变了我的在线办公方式。 让人惊…...
美创科技入选2024数字政府解决方案提供商TOP100!
11月19日,国内专业咨询机构DBC德本咨询发布“2024数字政府解决方案提供商TOP100”榜单。美创科技凭借在政府数据安全领域多年的项目经验、技术优势与创新能力,入选收录。 作为专业数据安全产品与服务提供商,美创科技一直致力于为政府、金融、…...

七天掌握SQL--->第五天:数据库安全与权限管理
1.1 用户权限管理 用户权限管理是指控制用户对数据库的访问和操作权限。在MySQL中,可以使用GRANT和REVOKE命令来管理用户权限。 GRANT命令用于授予用户权限。语法如下: GRANT privileges ON database.table TO userhost IDENTIFIED BY password;其中&…...
:基于 Python 的 AdaBoost 分类模型)
数学建模学习(138):基于 Python 的 AdaBoost 分类模型
1. AdaBoost算法简介 AdaBoost(Adaptive Boosting)是一种经典的集成学习算法,由Yoav Freund和Robert Schapire提出。它通过迭代训练一系列的弱分类器,并将这些弱分类器组合成一个强分类器。算法的核心思想是:对于被错误分类的样本,在下一轮训练中增加其权重;对于正确分类…...

丹摩|丹摩智算平台深度评测
1. 丹摩智算平台介绍 随着人工智能和大数据技术的快速发展,越来越多的智能计算平台涌现,为科研工作者和开发者提供高性能计算资源。丹摩智算平台作为其中的一员,定位于智能计算服务的提供者,支持从数据处理到模型训练的全流程操作…...

『VUE』34. 异步组件(详细图文注释)
目录 加载速度的优化示例代码总结 欢迎关注 『VUE』 专栏,持续更新中 欢迎关注 『VUE』 专栏,持续更新中 加载速度的优化 实际项目中你可能会有几十个组件,如果一开始就加载了全部组件(哪怕其中有些组件你暂时用不到)这无疑大大增加了响应时间,用户体验…...
算法及python实现)
深入解析自校正控制(STC)算法及python实现
目录 深入解析自校正控制(STC)算法第一部分:自校正控制算法概述1.1 什么是自校正控制1.2 自校正控制的核心思想1.3 STC 的应用场景1.4 STC 的分类第二部分:自校正控制算法的数学基础2.1 动态系统模型2.2 参数辨识方法2.3 控制器设计2.4 稳定性分析第三部分:Python 实现自校…...

《macOS 开发环境配置与应用开发》
一、引言 macOS 作为一款强大而流行的操作系统,为开发者提供了丰富的开发机会和优秀的开发环境。无论是开发原生的 macOS 应用,还是进行跨平台开发,了解和掌握 macOS 开发环境的配置以及应用开发的方法至关重要。本文将详细介绍 macOS 开发环…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...
