算法日记 33 day 动态规划(打家劫舍,股票买卖)
今天来看看动态规划的打家劫舍和买卖股票的问题。
上题目!!!!
题目:打家劫舍
198. 打家劫舍 - 力扣(LeetCode)
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
题目分析:
对于每一房间其实只有两种状态,偷或不偷,而且这个状态也取决于之前偷没偷。五部曲分析。
dp[i]:小偷到第i间放的最大金额
i的两种状态(偷,不偷)
不偷:dp[i]=dp[i-1]
偷:dp[i]=dp[i-2]
dp[0]=nums[0] dp[1]=max(nums[0],nums[1])
public class Solution {public int Rob(int[] nums) {if(nums.Length==0) return 0;if(nums.Length==1) return nums[0];int[] dp=new int[nums.Length];dp[0]=nums[0];dp[1]=Math.Max(nums[0],nums[1]);for(int i=2;i<nums.Length;i++){dp[i]=Math.Max(dp[i-2]+nums[i],dp[i-1]);}return dp[nums.Length-1];}
}题目:打家劫舍 2
213. 打家劫舍 II - 力扣(LeetCode)
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
题目分析:
房子围城一圈,那么对于首尾的房子而言,我们只能偷一个,其他的房间呢则尽量偷。本质上就和上一题一样了,无非是偷的时候划分一下区间即可,其他部分完全一样。
public class Solution {public int Rob(int[] nums) {if(nums.Length==0) return 0;if(nums.Length==1) return nums[0];int res1=RobRange(nums,0,nums.Length-2);int res2=RobRange(nums,1,nums.Length-1);return Math.Max(res1,res2);}public int RobRange(int[] nums,int start,int end){if (end == start) return nums[start];int[] dp=new int[nums.Length];dp[start]=nums[start];dp[start+1]=Math.Max(nums[start],nums[start+1]);for(int i=start+2;i<=end;i++){dp[i]=Math.Max(dp[i-2]+nums[i],dp[i-1]);}return dp[end];}
}题目:打家劫舍 III
337. 打家劫舍 III - 力扣(LeetCode)
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
题目分析:
房子的排列变成了树形结构,那么不触发警报意味着,如果我们偷了一个结点,那么他的两个子节点都不能偷。
其实结点的状态任然是两种偷或者不偷。但是我们要偷取的金额最大,一定要考虑不偷这个的情况下,他的左右子节点偷不偷呢。所以需要将左右孩子的偷不偷的最大金额返回给父节点,那么对于这个树的遍历只能使用后序遍历的方式。
public class Solution {public int Rob(TreeNode root) {int[] res=RobTrue(root);return Math.Max(res[1],res[0]);}public int[] RobTrue(TreeNode root){if(root==null) return new int[2]{0,0};int[] leftDp=RobTrue(root.left);int[] rightDp=RobTrue(root.right);//下标为0记录不偷该节点所得到的的最大金钱,下标为1记录偷该节点所得到的的最大金钱。int res1=root.val+leftDp[0]+rightDp[0];//偷这个结点加上不偷左右孩子的最大值int res2=Math.Max(leftDp[0],leftDp[1])+Math.Max(rightDp[0],rightDp[1]);//不偷这个结点,就考虑左右孩子要不要偷return new int[]{res2,res1};}
}题目:买卖股票的最佳时机
121. 买卖股票的最佳时机 - 力扣(LeetCode)
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
题目分析:
这一题可以用暴力和贪心的方法解决。
暴力,依次枚举股票价格,并且找出最大差值作为结果即可。
贪心的想法很自然就是取最左最小值,取最右最大值,那么得到的差值就是最大利润。
两者差不多。
public class Solution {public int MaxProfit(int[] prices) {int min=int.MaxValue;int res=0;for(int i=0;i<prices.Length;i++){min=Math.Min(prices[i],min);res=Math.Max(res,prices[i]-min);}return res;}
}动态规划:
考虑股票的状态,其实就只有持有和不持有两种状态。注意这里的持有和不持有并不是买入卖出的意思。来看看dp数组的解释。
dp[i][0]:在第i天这支股票在我手上持有的最大金额(利润)
dp[i][1]:在第i天这支股票不在我手上持有的最大金额(利润)
注意两个的区别,因为这个持有和不持有他需要考虑前一天的状态,也就是说在这一天之前,这个股票我可能已经买入或者卖出了。这个很重要。
递推公式:
持有股票(1.在这一天之前我就持有了 2,之前我没有,但是今天买入后持有了)
1.dp[i-1][0] 2.-price[i]
dp[i][0]=max(dp[i-1][0],-price[i])
不持有股票(1.在这一天之前我就没有了 2,之前我有,但是今天卖了后就没有了)
1.dp[i-1][1] 2.dp[i-1][0]+price[i]
dp[i][0]=max(dp[i-1][1] ,dp[i-1][0]+price[i])
初始化就很好理解了,那么来看看代码
public class Solution {public int MaxProfit(int[] prices) {int[,] dp=new int[prices.Length,2];dp[0,0]=-prices[0];//持有这个股票dp[0,1]=0;//不持有这个股票for(int i=1;i<prices.Length;i++){dp[i,0]=Math.Max(-prices[i],dp[i-1,0]);dp[i,1]=Math.Max(dp[i-1,0]+prices[i],dp[i-1,1]);}return Math.Max(dp[prices.Length-1,0],dp[prices.Length-1,1]);}
}题目:买卖股票的最佳时机II
122. 买卖股票的最佳时机 II - 力扣(LeetCode)
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
题目分析:
注意和上一题的区别,题目中的每一天意味着我可以多次买入卖出。但是上一题我只能操作一次。
这里的dp的含义和上一题一样的,区别是dp的递推公式。
递推公式:
持有股票(1.在这一天之前我就持有了 2,(可能我已经卖出过了)之前我没有,但是今天买入后持有了)
1.dp[i-1][0] 2.dp[i-1][1]-price[i](上一天是不持有的状态)
dp[i][0]=max(dp[i-1][0],dp[i-1][1]-price[i])
不持有股票(1.在这一天之前我就没有了 2,之前我有,但是今天卖了后就没有了)
1.dp[i-1][1] 2.dp[i-1][0]+price[i]
dp[i][0]=max(dp[i-1][1] ,dp[i-1][0]+price[i])
public class Solution {public int MaxProfit(int[] prices) {int[,] dp=new int[prices.Length,2];dp[0,0]=-prices[0];//持有这个股票dp[0,1]=0;//不持有这个股票for(int i=1;i<prices.Length;i++){dp[i,0]=Math.Max(dp[i-1,1]-prices[i],dp[i-1,0]);dp[i,1]=Math.Max(dp[i-1,0]+prices[i],dp[i-1,1]);}return Math.Max(dp[prices.Length-1,0],dp[prices.Length-1,1]);}
}主要区别在于持有股票是需要考虑之前是否有卖出过,这一点在下面的题中很重要
题目:买卖股票的最佳时机III
123. 买卖股票的最佳时机 III - 力扣(LeetCode)
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
题目分析:
会看前面两题,第一题要求只能买入卖出1次,第二题能买入卖出无数次。而这一题最多两次,和上面两题一样,看看股票在第i天可能出现的状态。
第一次买入
第一次卖出
第二次买入
第二次卖出
那么dp数组的含义就很好理解了。
来看看递推公式,本质上和上面的题是一样的,无非就是买入卖出的时候需要考虑之前的状态,这一点和第二题一样。
达到dp[i][1]状态,有两个具体操作:
- 操作一:第i天买入股票了,那么dp[i][1] = dp[i-1][0] - prices[i]
- 操作二:第i天没有操作,而是沿用前一天买入的状态,即:dp[i][1] = dp[i - 1][1]
那么dp[i][1]究竟选 dp[i-1][0] - prices[i],还是dp[i - 1][1]呢?
一定是选最大的,所以 dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);
同理dp[i][2]也有两个操作:
- 操作一:第i天卖出股票了,那么dp[i][2] = dp[i - 1][1] + prices[i]
- 操作二:第i天没有操作,沿用前一天卖出股票的状态,即:dp[i][2] = dp[i - 1][2]
所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])
同理可推出剩下状态部分:
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
对于初始化而言,需要注意的是你可以在一天内多次买入卖出,因为price的长度可以为1。
public class Solution {public int MaxProfit(int[] prices) {int[,] dp=new int[prices.Length,5];dp[0,0]=0;//0,不操作dp[0,1]=-prices[0];//1,第一次持有dp[0,2]=0;//2,第一次不持有dp[0,3]=-prices[0];//3,第二次持有dp[0,4]=0;//4,第二次不持有for(int i=1;i<prices.Length;i++){dp[i,1]=Math.Max(dp[i-1,1],-prices[i]);dp[i,2]=Math.Max(dp[i-1,1]+prices[i],dp[i-1,2]);dp[i,3]=Math.Max(dp[i-1,3],dp[i,2]-prices[i]);dp[i,4]=Math.Max(dp[i-1,4],dp[i-1,3]+prices[i]);}return Math.Max(dp[prices.Length-1,4],dp[prices.Length-1,2]);}
}
对于更详细的解析与其他语言的代码块,可以去代码随想录上查看。
代码随想录 (programmercarl.com)
已刷题目:110
相关文章:
)
算法日记 33 day 动态规划(打家劫舍,股票买卖)
今天来看看动态规划的打家劫舍和买卖股票的问题。 上题目!!!! 题目:打家劫舍 198. 打家劫舍 - 力扣(LeetCode) 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金…...

JavaScript的let、var、const
这张图片主要介绍了JavaScript中的三种变量声明方式:let、var和const。 1. let 含义:let是现在实际开发中常用的变量声明方式。特点: 块级作用域:let声明的变量只在其所在的块级作用域内有效。例如:{let x 10; } co…...

C语言-数学基础问题
一.奇数、偶数问题 1.从键盘上输入一个整数,判断并输出它是奇数还是偶数。 //从键盘上输入一个整数,判断并输出它是奇数还是偶数。 main() {int i;printf("输入一个整数:\n");scanf("%d",&i);if(i%20)printf("它是偶数\n…...

解决单元测试时找不到类名
场景: springboot单元测试mockito对mapper进行mock时: tk.mybatis.mapper.mapperexception: 无法获取实体类 XX.xx 对应的表名 分析: 使用了一个方法:Example examplenew Example(User.class); 进入源码后发现Entityhelper没…...

从零开始-VitePress 构建个人博客上传GitHub自动构建访问
从零开始-VitePress 构建个人博客上传GitHub自动构建访问 序言 VitePress 官网:VitePress 中文版 1. 什么是 VitePress VitePress 是一个静态站点生成器 (SSG),专为构建快速、以内容为中心的站点而设计。简而言之,VitePress 获取用 Markdown…...

【案例学习】如何使用Minitab实现包装过程的自动化和改进
Masimo 是一家全球性的医疗技术公司,致力于开发和生产各种行业领先的监控技术,包括创新的测量、传感器和患者监护仪。在 Masimo Hospital Automation 平台的助力下,Masimo 的连接、自动化、远程医疗和远程监控解决方案正在改善医院内外的护理…...

【ArcGISPro】使用AI提取要素-土地分类(sentinel2)
Sentinel2数据处理 【ArcGISPro】Sentinel-2数据处理-CSDN博客 土地覆盖类型分类 处理结果...

深度解析:Nginx模块架构与工作机制的奥秘
文章目录 前言Nginx是什么?Ngnix特点: 一、Nginx模块与工作原理1.Nginx的模块1.1 Nginx模块常规的HTTP请求和响应的流程图:1.2 Nginx的模块从结构上分为如下三类:1.3 Nginx的模块从功能上分为如下三类: 2.Nginx的进程模型2.1 Nginx进程结构2.2 nginx进程…...

分布式kettle调度平台v6.4.0新功能介绍
介绍 Kettle(也称为Pentaho Data Integration)是一款开源的ETL(Extract, Transform, Load)工具,由Pentaho(现为Hitachi Vantara)开发和维护。它提供了一套强大的数据集成和转换功能,…...

企业数字化转型现状
国家数字经济战略背景 2018年以来,国家政府不断出台政策规范我国企业数字化治理市场。2018年9月颁布《关于发展数字经济稳定并扩大就业的指导意见》,支持建设一批数字经济创新创业孵化机构。积极推进供应链创新与应用,支持构建以企业为主导。…...

极客大挑战2024wp
极客大挑战2024wp web 和misc 都没咋做出来,全靠pwn✌带飞 排名 密码学和re没做出几个,就不发了 web ez_pop 源代码 <?php Class SYC{public $starven;public function __call($name, $arguments){if(preg_match(/%|iconv|UCS|UTF|rot|quoted…...

将django+vue项目发布部署到服务器
1.部署django后端服务 部署架构 1.1 下载依赖插件 pip3.8 freeze > requirements.txt1.2 安装依赖插件 pip3 install -r requirements.txt1.3 安装mysql数据库 apt install mysql-server初始化数据库 CREATE USER admin% IDENTIFIED WITH mysql_native_password BY 123…...

函数类型注释和Union联合类型注释
函数类型注释格式(调用时提示输入参数的类型): )def 函数名(形参名:类型,形参名:类型)->函数返回值类型: 函数体 Union联合类型注释(可注释多种类型混合的变量)格式: #先导入模块 from typing import…...

python画图|无坐标轴自由划线操作fig.add_artist(lines.Line2D()函数
【1】引言 新发现了一种自由划线操作函数,和大家共享。 【2】官网教程 点击下述代码,直达官网: https://matplotlib.org/stable/gallery/misc/fig_x.html#sphx-glr-gallery-misc-fig-x-py 官网代码非常简洁,我进行了解读。 …...

MacOS系统上Jmeter 录制脚本遇到的证书坑位
一、JMeter介绍与安装 1,下载及安装 jmeter官网地址 二、录制百度链接https请求时,需要导入jmeter相关证书到macos系统的更目录中. 导入方式,直接拖入mac的系统中,始终新人就可以; 三、jmeter 创建相关的录制组件…...

网络层协议IP
对于网络层我们直接通过IP协议来了解其内容 一.IP协议 首先我们先来了解几个概念: 主机:配有IP地址,但是不进行路由控制的设备 路由器:配有IP地址,同时进行路由控制的设备 节点:主机和路由器的统称 所以现在…...
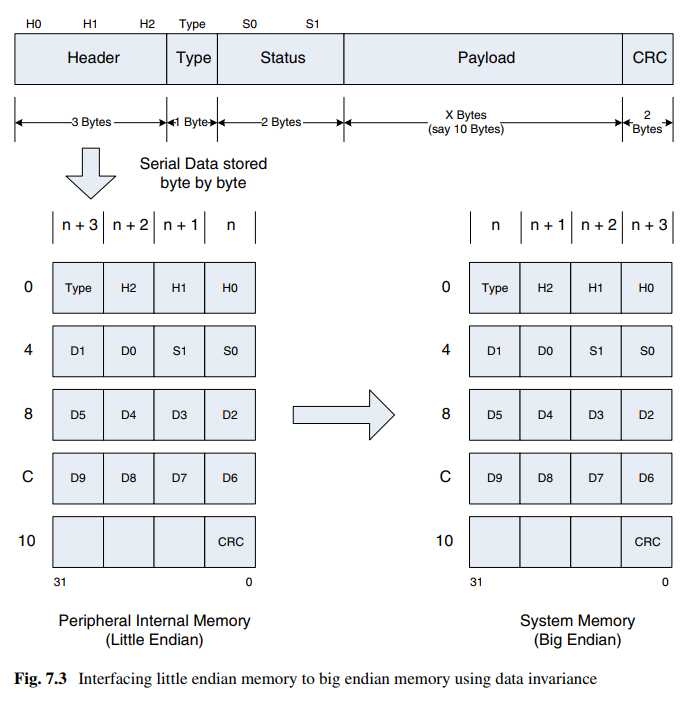
《硬件架构的艺术》笔记(七):处理字节顺序
介绍 本章主要介绍字节顺序的的基本规则。(感觉偏软件了,不知道为啥那么会放进《硬件架构的艺术》这本书)。 定义 字节顺序定义数据在计算机系统中的存储格式,描述存储器中的MSB和LSB的位置。对于数据始终以32位形式保存在存储器…...

反向代理模块
1 概念 1.1 反向代理概念 反向代理是指以代理服务器来接收客户端的请求,然后将请求转发给内部网络上的服务器,将从服务器上得到的结果返回给客户端,此时代理服务器对外表现为一个反向代理服务器。 对于客户端来说,反向代理就相当于…...

风尚云网前端学习:一个简易前端新手友好的HTML5页面布局与样式设计
风尚云网前端学习:一个简易前端新手友好的HTML5页面布局与样式设计 简介 在前端开发的世界里,HTML5和CSS3是构建现代网页的基石。本文将通过一个简单的HTML5页面模板,展示如何使用HTML5的结构化元素和CSS3的样式特性,来创建一个…...

spacy 安装 en_core_web_sm
目录 spacy win11 成功 linux No matching distribution found for numpy<3.0.0,>2.0.0 解决方法: linux安装失败: linux安装成功 从GitHub上下载 spacy win11 成功 pip install -i https://pypi.tuna.tsinghua.edu.cn/simple spacy linux N…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...

自定义线程池1.2
自定义线程池 1.2 1. 简介 上次我们实现了 1.1 版本,将线程池中的线程数量交给使用者决定,并且将线程的创建延迟到任务提交的时候,在本文中我们将对这个版本进行如下的优化: 在新建线程时交给线程一个任务。让线程在某种情况下…...
