软件工程(4)--螺旋模型
前言
这是基于我所学习的软件工程课程总结的第四篇文章。
在软件开发过程中必须及时识别和分析风险,并且采取适当措施以消除或减少风险的危害。构建原型是一种能使某些类型的风险降至最低的方法。为了降低交付给用户的产品不能满足用户需要的风险,一种行之有效的方法是在需求分析阶段快速地构建一个原型。在后续的阶段中也可以通过构造适当的原型来降低某些技术风险。当然,原型并不能"包治百病",对于某些类型的风险(例如,聘请不到需要的专业人员或关键的技术人员在项目完成前"跳槽"),原型方法是无能为力的。
螺旋模型的基本思想是,使用原型及其他方法来尽量降低风险。理解这种模型的一个简便方法,是把它看作在每个阶段之前都增加了风险分析过程的快速原型模型。(摘自 《软件工程导论》第六版 张海藩 牟永敏 著,有删改)
正文
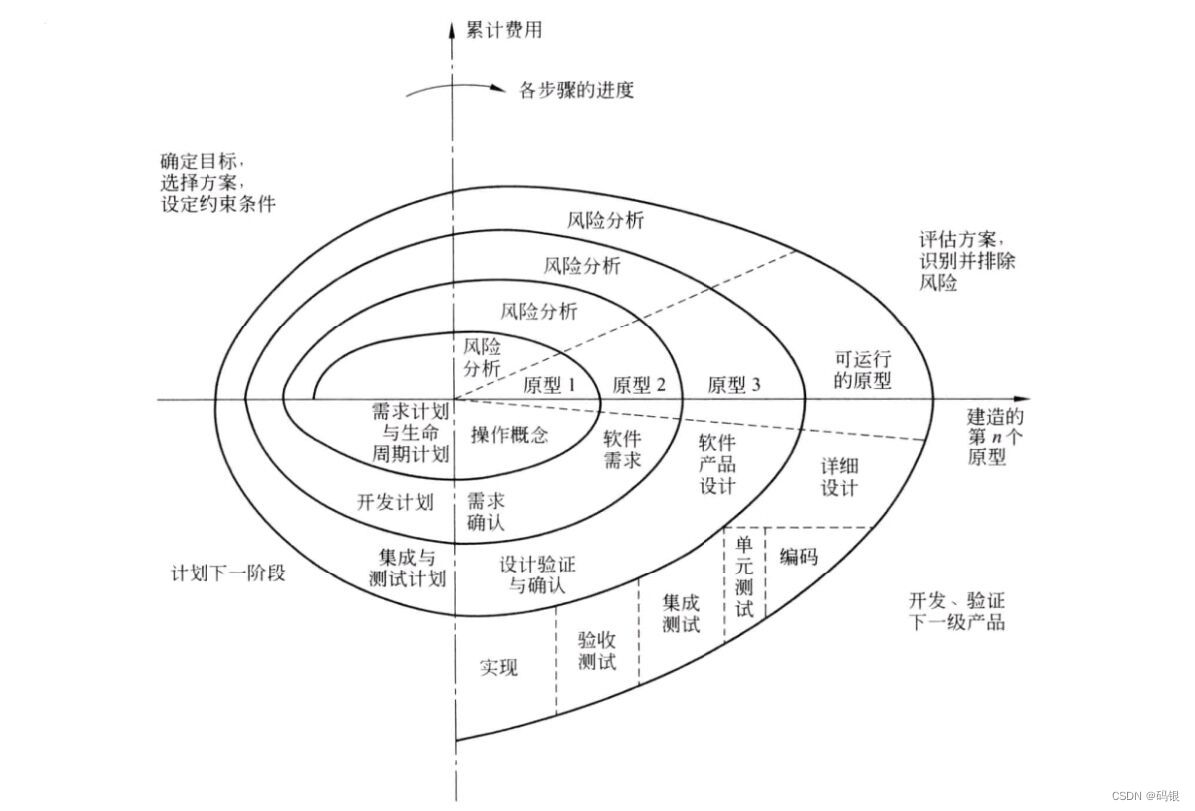
1.螺旋模型 (spiral model)
·软件开发普遍存在风险。
交付的产品用户不满意.
产品不能按时交付.
开发成本超过预算.
产品开发期间关键开发人员离职.
产品投入市场前竞争对手发布功能相近价格更低产品.
·把开发活动和风险管理结合起来控制风险。
·开发过程分成若干次迭代,每次迭代代表开发的一个阶段,对应模型中一条环线。
每次迭代分成四个方面的活动,对应笛卡尔坐标的四个象限:
确定本阶段目标,选定实施方案,弄清项目开发的限制条件;
评估所选方案,通过构造原型和风险分析识别和消除风险;
实施软件开发和验证;
评价本阶段的工作成果,提出修正建议,并计划下一阶段工作。
·模型结合了瀑布模型和原型模型的特点。
·在螺旋模型中维护只是模型的另一个周期,在维护和开发之间并没有本质的区别。
·软件模型的主要优势在于,他是风险驱动的,但这也可能是他的一个缺点(开发人员最好有相当丰富的风险评估经验和专门知识)。
螺旋模型
2.螺旋模型的优点
- 螺旋模型强调原型的可扩充性和可修改性,原型的进化贯穿整个软件生存周期,这将有助于目标软件的适应能力,支持用户需求的动态变化;
- 原型可看作可执行的需求规格说明,易于为用户和开发人员共同理解,还可作为继续开发的基础,并为用户参与所有关键决策提供了方便;
- 螺旋模型为项目管理人员及时调整管理决策提供了方便,进而可降低开发风险。
- 减少了过多测试或测试不足所带来的风险。
- 对可选方案和约束条件的强调有利于已有软件的重用,也有助于把软件质量作为软件开发的一个重要目标。
3.螺旋模型的缺点
- 如果每次迭代的效率不高,致使迭代次数过多,将会增加成本并推迟交付时间
- 使用该模型需要有相当丰富的风险评估经验和专门知识,要求开发队伍水平较高,否则会带来更大风险,可能项目实际走向灾难时,开发人员还以为一切正常。
4.螺旋模型的适用场合
- 适用于需求不明确或者需求可能发生变化的大型复杂的软件系统。
- 支持面向过程、面向对象等多种软件开发方法,是一种具有广阔前景的模型。
- 适用于大规模内部开发项目,分析风险和排除风险
5.小测
包含风险分析的软件工程模型是(D)
A. 喷泉模型 B. 瀑布模型 C. 增量模型 D. 螺旋模型
相关文章:
软件工程(4)--螺旋模型
前言 这是基于我所学习的软件工程课程总结的第四篇文章。 在软件开发过程中必须及时识别和分析风险,并且采取适当措施以消除或减少风险的危害。构建原型是一种能使某些类型的风险降至最低的方法。为了降低交付给用户的产品不能满足用户需要的风险,一种行…...

图解LeetCode——剑指 Offer 50. 第一个只出现一次的字符
一、题目 在字符串 s 中找出第一个只出现一次的字符。如果没有,返回一个单空格。 s 只包含小写字母。 二、示例 2.1> 示例 1: 【输入】s "abaccdeff" 【输出】b 2.2> 示例 2: 【输入】s "" 【输出】 限制: 0 < s 的…...

《HTML 5与CSS 3核心技法》读书笔记
目录前言第1章 写在前面第2章 HTML 语法基础第3章 布局类元素 ,房子的楼板、柱子和大梁第4章 功能类元素,房子的门、窗、水管和电气第5章 CSS基础第6章 选择器,确定样式的作用范围选择器类型选择器的组合使用第7章 权重,样式发送冲…...

【沐风老师】3DMAX几何投影插件Geometry Projection使用详解
【几何投影插件】 描述 3DMAX几何投影插件Geometry Projection,将一个或多个对象或它的顶点选择沿全局或局部 x、y 或 z 轴投影到另一个对象上。 适用版本 3dMax2013或更高版本 安装设置 插件的安装非常简单,解压后把插件脚本 “geometry_projectio…...

面试问题整理
20200422面试题 1、有nginx为什么还要用gateway 2、factorybean和beanfactory有什么区别 https://www.cnblogs.com/leeego-123/p/12159574.html 2、aop原理 3、ioc原理 4、注解requestbody和responsebody区别。pathvireable和requestparam注解区别,feign客户端的注解…...

“区块链60人”2022赋能中国区块链创新人物名单公布
2022年11月5日,“2022第五届全国高校人工智能大数据区块链教育教学创新论坛”在京隆重召开。此次论坛公布了“区块链60人”2022赋能中国区块链创新人物评选活动获评名单。 本次评选活动通过媒体报道、第三方推荐、专家评选等环节,坚持“公开、公平、公正…...

day2324 数组
文章目录相关概念codeArrayTest08 数组拷贝相关概念 day23课堂笔记 1、数组 1.1、数组的优点和缺点,并且要理解为什么。 第一:空间存储上,内存地址是连续的。 第二:每个元素占用的空间大小相同。 第三:知道首元素的内…...

【Python实战】神仙运气—快看看你的彩票:2千多万元大奖无人领,马上就过期了,下一期的中奖者会是你吗?(纯技术交流)
前言 越努力越幸运 哈喽~我是栗子同学! 特别注意:不管是沉迷赌球,还是沉迷购彩,都是不可取的。本文纯是一个技术学习内容。 听说关注我的人会暴富哦!、 所有文章完整的素材源码都在👇👇 粉丝…...

2023年上半年软考高项信息系统项目管理师2月25日开班
信息系统项目管理师是全国计算机技术与软件专业技术资格(水平)考试(简称软考)项目之一,是由国家人力资源和社会保障部、工业和信息化部共同组织的国家级考试,既属于国家职业资格考试,又是职称资…...
数据库(第一天)
文档信息 文档类别正式文档文档编号数据库基础课 1.2-001版本1.2-001文档名称数据库基础课编写负责人/编写时间梁昭东/2023 年 1 月 30 日审核负责人/审核时间年 月 日批准人/批准时间年 月 日 变更记录 日期版本号变更内容修订者2023.01.30v1.2版根据实际情况增删了部分内容…...

一文了解 ArrayList 的扩容机制
了解 ArrayList 在 Java 中常用集合类之间的关系如下图所示: 从图中可以看出 ArrayList 是实现了 List 接口,并是一个可扩容数组(动态数组),它的内部是基于数组实现的。它的源码定义如下: public class A…...

牛态已成选股源码
{牛态已成} {条件选股} {其他类型} N:7; A1:(REF(H,N) HHV(H,((2 * N) 1))); B1:FILTER(A1,N); C1:BACKSET(B1,(N 1)); D1:FILTER(C1,N); A2:(REF(L,N) LLV(L,((2 * N) 1))); B2:FILTER(A2,N); C2:BACKSET(B2,(N 1)); D2:FILTER(C2,N); E1:((REF(LLV(L,(2 * N)),1) REF(…...

Python基础
Python 是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。Python 的设计具有很强的可读性,相比其他语言经常使用英文关键字,其他语言的一些标点符号,它具有比其他语言更有特色语法结构。小编也整理了一套关于学习Python入门…...

浅显易懂的说清楚小游戏与H5游戏的技术区别
从“跳一跳”到“羊了个羊”微信小游戏上线4年时间,除了涌现出不少火爆全网的小游戏之外,也有类似于“动物餐厅”、“口袋奇兵”等游戏得以在此孵化繁荣,凭借着微信强大的社交属性小游戏成为游戏厂商在桌面端、App 端、H5 端之外争夺的另一个…...
【Python入门第七天】Python 数字
Python 数字 Python 中有三种数字类型: intfloatcomplex 为变量赋值时,将创建数值类型的变量: 实例 x 10 # int y 6.3 # float z 2j # complex如需验证 Python 中任何对象的类型,请使用 type() 函数: 实…...
,看完可就业)
Python自动化测试 软件测试最全教程(附笔记),看完可就业
最近看到很多粉丝在后台私信我,叫我做一期Python自动化测试的教程,其实关于这个问题,我也早就在着手准备了,我录制了一整套完整的Python自动化测试的教程,都上传在B站上面,大家有兴趣的可以去看一下&#x…...
Windows 安装Tomcat
版本:tomcat8.5jdk-8u231一.解压JDK安装包 更换JDK安装路径二.解压安装Tomcat 选择jdk安装路径更换tomcat安装路径三.设置环境变量 1.“环境变量”界面中系统变量点击”新建“,创建CATALINA_HOMEC:\RESSET\tomcat(Tomcat服务器的根目录)2.创建…...
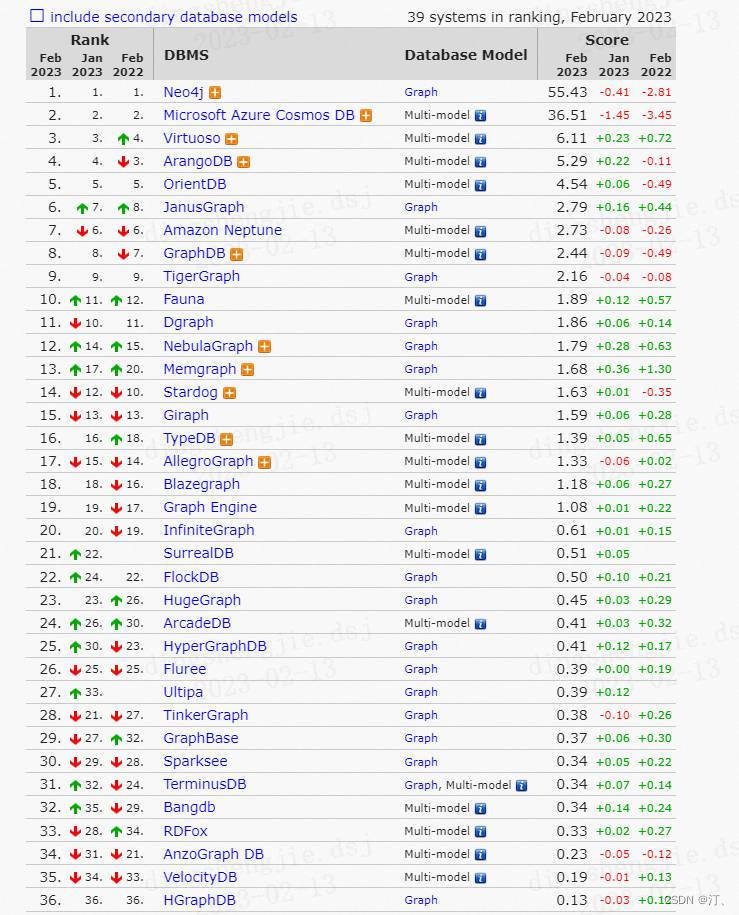
知识图谱业务落地技术推荐之图数据库汇总
0.图数据库排名 链接:https://db-engines.com/en/ranking/graph+dbms 0.1简要分析(各种图数据库属性) Neo4j(主流) 历史悠久且...
 | 刷完必过)
2023新华为OD机试题 - 最小传递延迟(JavaScript) | 刷完必过
最小传递延迟 题目 通讯网络中有N个网络节点 用1 ~ N进行标识 网络通过一个有向无环图进行表示 其中图的边的值,表示节点之间的消息传递延迟 现给定相连节点之间的延时列表times[i]={u,v,w} 其中u表示源节点,v表示目的节点,w表示u和v之间的消息传递延时 请计算给定源节点到…...
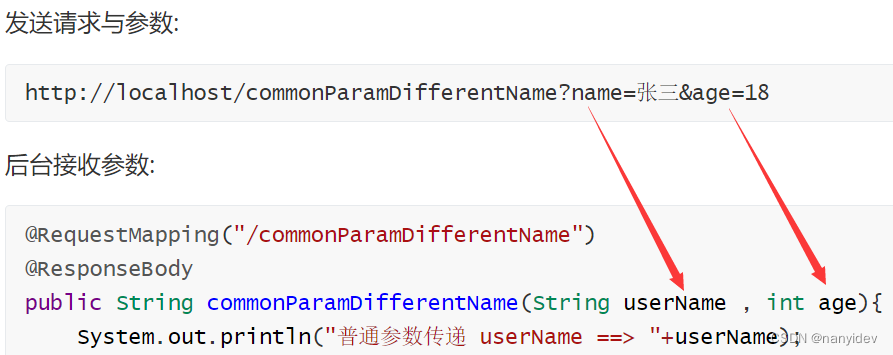
SpringMVC基础入门(一)之理论基础概念
文章目录SpringMVC1.概念2.常用注解请求与响应1.请求参数2.JSON传输3.常用注解响应1.响应页面2.响应JSON数据Rest风格1.介绍2.常用注解SpringMVC 1.概念 (1)定义 SpringMVC是一种基于Java实现MVC模型的轻量级Web框架。 (2)为什…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

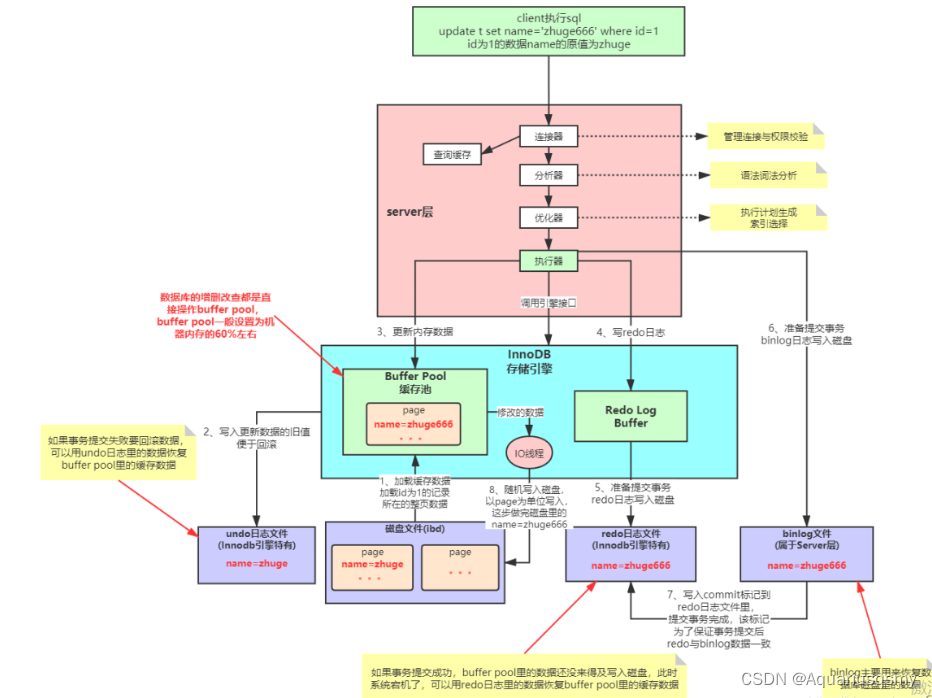
Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
