深度优先搜索迷宫路径
深度优先搜索迷宫路径
问题描述
我们需要编写一个程序,通过深度优先搜索(DFS)找到从迷宫左上角到右下角的一条通路。
-
迷宫的表示:
- 迷宫由 0 和 1 构成的二维数组表示。
0表示可以走的路径,1表示障碍。- 用户输入迷宫的行列数和迷宫的内容。
-
功能需求:
- 找到一条从左上角到右下角的路径。
- 如果路径存在,用
*标记路径并打印迷宫。 - 如果路径不存在,打印提示信息。
代码实现思路
1. 核心算法
我们使用深度优先搜索(DFS)来遍历迷宫:
- 优先级:右 → 下 → 左 → 上。
- 使用栈存储路径:
- 当前节点可以继续探索时,入栈。
- 如果遇到死路,则回退(出栈)。
2. 数据结构
-
节点 (
Node):- 坐标
(x, y)。 - 值 (
value):通路 (PATH) 或障碍 (WALL)。 - 四个方向的行走状态 (
direction):是否可以向右、下、左、上移动。
- 坐标
-
迷宫 (
Maze):- 包含节点的二维数组。
- 动态分配内存以支持不同大小的迷宫。
-
栈 (
std::stack):- 存储路径节点,便于回退操作。
3. 流程
-
输入:
- 用户输入行数和列数,随后输入迷宫数据。
-
初始化:
- 设置每个节点的方向状态(右、下、左、上是否可行)。
- 初始化所有节点的值(
PATH或WALL)。
-
搜索路径:
- 如果入口或出口为障碍 (
WALL),直接输出“无路径”。 - 否则,从起点
(0, 0)开始搜索:- 判断当前节点四个方向是否可行。
- 可行方向入栈;不可行则回退(出栈)。
- 如果入口或出口为障碍 (
-
输出:
- 如果找到路径,打印迷宫,将路径标记为
*。 - 如果找不到路径,提示“无路径”。
- 如果找到路径,打印迷宫,将路径标记为
完整代码
#include <iostream>
#include <stack>// 定义方向常量
enum Direction { RIGHT = 0, DOWN, LEFT, UP };// 定义状态常量
const int YES = 4; // 表示该方向可走
const int NO = 5; // 表示该方向不可走// 定义迷宫单元状态
enum CellState { PATH = 0, WALL = 1 }; // PATH 表示通路,WALL 表示障碍// 节点结构体,表示迷宫中的一个单元
struct Node {int x, y; // 坐标CellState value; // 值:PATH 表示通路,WALL 表示障碍int direction[4]; // 四个方向:RIGHT, DOWN, LEFT, UP,值为 YES 表示能走,NO 表示不能走
};// 迷宫类
class Maze {
private:int rows, cols; // 迷宫行数和列数Node** grid; // 动态二维数组存储迷宫std::stack<Node*> path; // 栈,用于深度优先搜索路径public:Maze(int r, int c) : rows(r), cols(c) {grid = new Node*[rows];for (int i = 0; i < rows; ++i) {grid[i] = new Node[cols];}}~Maze() {for (int i = 0; i < rows; ++i) {delete[] grid[i];}delete[] grid;}// 初始化迷宫void initializeMaze() {std::cout << "Enter the maze (0 for path, 1 for obstacle):\n";for (int i = 0; i < rows; ++i) {for (int j = 0; j < cols; ++j) {int value;std::cin >> value;grid[i][j].value = (value == 0) ? PATH : WALL; // 使用枚举替代数字grid[i][j].x = i;grid[i][j].y = j;for (int k = 0; k < 4; ++k) {grid[i][j].direction[k] = NO; // 初始状态不可走}}}}// 设置每个节点四个方向的状态void setNodeDirections() {for (int i = 0; i < rows; ++i) {for (int j = 0; j < cols; ++j) {if (grid[i][j].value == WALL) continue; // 如果是障碍,跳过// 右方向if (j + 1 < cols && grid[i][j + 1].value == PATH) grid[i][j].direction[RIGHT] = YES;// 下方向if (i + 1 < rows && grid[i + 1][j].value == PATH) grid[i][j].direction[DOWN] = YES;// 左方向if (j - 1 >= 0 && grid[i][j - 1].value == PATH) grid[i][j].direction[LEFT] = YES;// 上方向if (i - 1 >= 0 && grid[i - 1][j].value == PATH) grid[i][j].direction[UP] = YES;}}}// 深度优先搜索迷宫路径bool searchPath() {if (grid[0][0].value == WALL || grid[rows - 1][cols - 1].value == WALL) return false;path.push(&grid[0][0]); // 起点入栈while (!path.empty()) {Node* current = path.top();int x = current->x, y = current->y;// 判断是否到达终点if (x == rows - 1 && y == cols - 1) return true;bool moved = false;// 右方向if (current->direction[RIGHT] == YES && grid[x][y + 1].direction[LEFT] == YES) {current->direction[RIGHT] = NO;grid[x][y + 1].direction[LEFT] = NO;path.push(&grid[x][y + 1]);moved = true;}// 下方向else if (current->direction[DOWN] == YES && grid[x + 1][y].direction[UP] == YES) {current->direction[DOWN] = NO;grid[x + 1][y].direction[UP] = NO;path.push(&grid[x + 1][y]);moved = true;}// 左方向else if (current->direction[LEFT] == YES && grid[x][y - 1].direction[RIGHT] == YES) {current->direction[LEFT] = NO;grid[x][y - 1].direction[RIGHT] = NO;path.push(&grid[x][y - 1]);moved = true;}// 上方向else if (current->direction[UP] == YES && grid[x - 1][y].direction[DOWN] == YES) {current->direction[UP] = NO;grid[x - 1][y].direction[DOWN] = NO;path.push(&grid[x - 1][y]);moved = true;}if (!moved) path.pop(); // 如果四个方向都不能走,回退}return false; // 栈为空,未找到路径}// 打印迷宫路径void printPath() {// 将路径标记为 '*'while (!path.empty()) {Node* node = path.top();path.pop();grid[node->x][node->y].value = PATH; // 使用 PATH 表示路径}// 输出迷宫for (int i = 0; i < rows; ++i) {for (int j = 0; j < cols; ++j) {if (grid[i][j].value == PATH) {std::cout << '*';} else {std::cout << grid[i][j].value;}}std::cout << std::endl;}}
};int main() {int rows, cols;std::cout << "Enter maze dimensions (rows and columns): ";std::cin >> rows >> cols;Maze maze(rows, cols);maze.initializeMaze();maze.setNodeDirections();if (maze.searchPath()) {maze.printPath();} else {std::cout << "No path exists in the maze.\n";}return 0;
}
关键点总结
-
避免魔法数字:
- 使用
CellState(PATH,WALL) 表示单元状态。 - 使用
Direction枚举(RIGHT,DOWN,LEFT,UP)表示方向。
- 使用
-
清晰的逻辑:
- 每个方向的逻辑(右、下、左、上)清晰明确。
- 通过栈实现深度优先搜索,并在死路时回退。
-
动态分配二维数组:
- 根据用户输入动态分配内存,提高灵活性。
-
代码可读性高:
- 枚举和常量的使用,使代码更易读、更易维护。
-
扩展性强:
- 可轻松修改或增加方向、迷宫规则等逻辑。
运行示例
输入:
Enter maze dimensions (rows and columns): 5 5
Enter the maze (0 for path, 1 for obstacle):
0 1 0 0 0
0 1 0 1 0
0 0 0 1 0
0 1 1 1 0
0 0 0 0 0
输出:
*****0
*111*0
*000*0
*111*0
*****0
如果路径不存在,输出:
No path exists in the maze.
深度优先搜索(DFS)迷宫路径算法详细解释
DFS 基本概念
深度优先搜索(DFS)是一种用于遍历或搜索图或树结构的算法。它优先沿着每一个可能的分支路径深入,直到到达不可再继续的节点,然后回退(回溯)到上一个节点,探索未访问的分支。
在迷宫路径问题中,可以将迷宫看作一个二维网格,每个格子是一个节点,相邻的格子通过边连接。DFS 的目标是在起点和终点之间找到一条路径。
问题描述
-
输入:
- 一个二维数组表示迷宫:
0表示可以通行的路径。1表示障碍,不能通行。
- 起点
(0, 0)和终点(rows-1, cols-1)。
- 一个二维数组表示迷宫:
-
目标:
- 找到一条从起点到终点的路径。
- 如果找到路径,用
*标记路径并打印迷宫。 - 如果不存在路径,打印“无路径”。
DFS 核心思想
-
递归或栈实现:
- DFS 通过递归或栈来模拟路径搜索。
- 每次探索当前节点的某个方向,如果该方向可以走,就继续深入。
- 如果到达死胡同,则回退到上一个节点,探索其他未访问的方向。
-
避免重复访问:
- 在每次移动到新节点时,标记当前节点为“已访问”,防止重复探索和回头路。
- 可以通过修改节点状态或方向状态实现。
-
终止条件:
- 如果到达终点
(rows-1, cols-1),返回成功。 - 如果所有路径都探索完仍未到达终点,返回失败。
- 如果到达终点
DFS 算法步骤
-
初始化迷宫:
- 输入迷宫的大小和内容。
- 用
Node结构表示迷宫中的每个格子,存储格子的坐标、状态(路径或障碍)以及四个方向的可行性。
-
设置方向优先级:
- 使用固定顺序:右(Right)、下(Down)、左(Left)、上(Up)。
- 通过数组
dx和dy表示方向的坐标变化,例如:- 右:
dx = 0, dy = 1 - 下:
dx = 1, dy = 0
- 右:
-
搜索过程:
- 从起点
(0, 0)开始,将其加入路径栈。 - 按顺序检查四个方向:
- 如果某方向可以走:
- 标记当前节点的方向为不可走。
- 标记相邻节点从当前方向来的状态为不可走。
- 将相邻节点入栈。
- 继续深入探索。
- 如果四个方向都不能走,则回退(出栈),返回上一个节点继续探索。
- 如果某方向可以走:
- 从起点
-
终止条件:
- 找到终点时,路径栈中的节点即为完整路径。
- 栈为空时,表示无路径。
-
输出路径:
- 如果找到路径,打印迷宫并用
*标记路径。 - 如果无路径,打印提示信息。
- 如果找到路径,打印迷宫并用
伪代码
DFS(迷宫, 起点, 终点):如果起点或终点是障碍:返回“无路径”栈.push(起点)while 栈不为空:当前节点 = 栈顶如果当前节点是终点:返回路径否则:按顺序检查当前节点的 4 个方向:如果某方向可走:- 更新当前节点和相邻节点的状态(防止回头路)- 相邻节点入栈- 跳过后续方向(break)如果所有方向都不能走:当前节点出栈(回退)如果循环结束仍未找到终点:返回“无路径”
详细过程解析
假设迷宫如下:
0 1 0 0 0
0 1 0 1 0
0 0 0 1 0
0 1 1 1 0
0 0 0 0 0
-
起点
(0, 0)入栈:- 栈:
[(0, 0)]。 - 从
(0, 0)开始按顺序探索:- 右:障碍。
- 下:可走,入栈。
- 栈:
-
当前节点
(1, 0):- 栈:
[(0, 0), (1, 0)]。 - 按顺序探索:
- 右:障碍。
- 下:可走,入栈。
- 栈:
-
当前节点
(2, 0):- 栈:
[(0, 0), (1, 0), (2, 0)]。 - 按顺序探索:
- 右:可走,入栈。
- 栈:
-
当前节点
(2, 1):- 栈:
[(0, 0), (1, 0), (2, 0), (2, 1)]。 - 按顺序探索:
- 右:可走,入栈。
- 栈:
-
当前节点
(2, 2):- 栈:
[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2)]。 - 按顺序探索:
- 右:障碍。
- 下:可走,入栈。
- 栈:
-
当前节点
(3, 2):- 栈:
[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (3, 2)]。 - 按顺序探索:
- 右:障碍。
- 下:可走,入栈。
- 栈:
-
当前节点
(4, 2):- 栈:
[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (3, 2), (4, 2)]。 - 按顺序探索:
- 右:可走,入栈。
- 栈:
-
终点
(4, 4)入栈:- 栈:
[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (3, 2), (4, 2), (4, 3), (4, 4)]。 - 到达终点,结束搜索。
- 栈:
关键点详解
-
方向状态的更新:
- 每次移动后:
- 当前节点的方向标记为不可走,防止重复访问。
- 相邻节点的回头方向标记为不可走,防止回头。
- 每次移动后:
-
栈的作用:
- 栈保存当前路径节点,用于实现深度优先搜索。
- 当节点无法前进时,回退到上一个节点继续探索。
-
搜索优先级:
- 使用固定的方向顺序(右、下、左、上)确保路径唯一性。
-
边界条件:
- 起点或终点为障碍时,直接返回。
- 每次移动前检查坐标是否越界。
时间与空间复杂度
-
时间复杂度:
- 每个节点最多被访问一次,复杂度为
O(n * m),其中n是行数,m是列数。
- 每个节点最多被访问一次,复杂度为
-
空间复杂度:
- 栈中最多存储所有节点,复杂度为
O(n * m)。
- 栈中最多存储所有节点,复杂度为
避免回头路的原理
-
每个节点的方向状态:
- 每个节点有四个方向(右、下、左、上),用一个数组
direction[4]表示:YES表示该方向可以走。NO表示该方向不可走。
- 每个节点有四个方向(右、下、左、上),用一个数组
-
双向更新:
- 从当前节点走到相邻节点时:
- 更新当前节点的该方向状态为
NO,表示不能再次从该方向出发。 - 同时,更新相邻节点从回头方向来的状态为
NO,表示不能回到当前节点。
- 更新当前节点的该方向状态为
- 从当前节点走到相邻节点时:
-
目的:
- 通过双向更新,防止程序进入重复探索(例如节点之间循环往返)。
实现方式
以下代码展示了如何避免回头路(取右方向为例):
if (current->direction[RIGHT] == YES && grid[x][y + 1].direction[LEFT] == YES) {// 当前节点的右方向设置为不可走current->direction[RIGHT] = NO;// 相邻节点的左方向设置为不可走grid[x][y + 1].direction[LEFT] = NO;// 将相邻节点入栈path.push(&grid[x][y + 1]);moved = true;
}
具体步骤:
- 检查当前节点
current的右方向是否可走(direction[RIGHT] == YES)。 - 检查相邻节点(右边节点)的左方向是否可走(
grid[x][y + 1].direction[LEFT] == YES)。- 这保证了两节点之间的状态一致。
- 更新状态:
- 当前节点的右方向设置为
NO。 - 右边节点的左方向设置为
NO。 - 双向标记,确保后续无法重复走该路径。
- 当前节点的右方向设置为
- 将右边节点入栈,继续探索。
避免回头路的完整逻辑
在四个方向(右、下、左、上)中,都应用类似逻辑。以下是完整实现:
// 右方向
if (current->direction[RIGHT] == YES && grid[x][y + 1].direction[LEFT] == YES) {current->direction[RIGHT] = NO;grid[x][y + 1].direction[LEFT] = NO;path.push(&grid[x][y + 1]);moved = true;
}
// 下方向
else if (current->direction[DOWN] == YES && grid[x + 1][y].direction[UP] == YES) {current->direction[DOWN] = NO;grid[x + 1][y].direction[UP] = NO;path.push(&grid[x + 1][y]);moved = true;
}
// 左方向
else if (current->direction[LEFT] == YES && grid[x][y - 1].direction[RIGHT] == YES) {current->direction[LEFT] = NO;grid[x][y - 1].direction[RIGHT] = NO;path.push(&grid[x][y - 1]);moved = true;
}
// 上方向
else if (current->direction[UP] == YES && grid[x - 1][y].direction[DOWN] == YES) {current->direction[UP] = NO;grid[x - 1][y].direction[DOWN] = NO;path.push(&grid[x - 1][y]);moved = true;
}
避免回头路的效果
-
走过的方向:
- 每次从一个节点走向另一个节点时,都会标记双向路径为“不可走”。
- 例如,从
(0, 0)走到(0, 1)后:(0, 0)的右方向direction[RIGHT]被标记为NO。(0, 1)的左方向direction[LEFT]被标记为NO。
-
防止重复探索:
- 在后续探索中,如果程序回退到
(0, 1),由于其左方向direction[LEFT]已标记为NO,程序不会再返回(0, 0)。
- 在后续探索中,如果程序回退到
-
避免循环:
- 如果没有双向标记,程序可能陷入循环(例如
(0, 0) → (0, 1) → (0, 0)不断往返)。
- 如果没有双向标记,程序可能陷入循环(例如
更新方向状态的逻辑图解
以下是避免回头路的具体过程,假设我们从 (0, 0) 开始探索:
初始状态:
方向状态 (0, 0):
RIGHT = YES, DOWN = YES, LEFT = NO, UP = NO
方向状态 (0, 1):
RIGHT = YES, DOWN = YES, LEFT = YES, UP = NO
第一次移动:从 (0, 0) → (0, 1)
- 当前节点
(0, 0)的RIGHT被设置为NO。 - 相邻节点
(0, 1)的LEFT被设置为NO。 - 节点
(0, 1)入栈。
更新后的状态:
方向状态 (0, 0):
RIGHT = NO, DOWN = YES, LEFT = NO, UP = NO
方向状态 (0, 1):
RIGHT = YES, DOWN = YES, LEFT = NO, UP = NO
第二次移动:从 (0, 1) → (1, 1)
- 当前节点
(0, 1)的DOWN被设置为NO。 - 相邻节点
(1, 1)的UP被设置为NO。 - 节点
(1, 1)入栈。
更新后的状态:
方向状态 (0, 1):
RIGHT = YES, DOWN = NO, LEFT = NO, UP = NO
方向状态 (1, 1):
RIGHT = YES, DOWN = YES, LEFT = YES, UP = NO
走到死胡同时的回退:
- 当一个节点的四个方向都不可走时,执行出栈操作,回到上一个节点。
- 回退时不会选择已标记为
NO的方向,避免重复探索。
相关文章:

深度优先搜索迷宫路径
深度优先搜索迷宫路径 问题描述 我们需要编写一个程序,通过深度优先搜索(DFS)找到从迷宫左上角到右下角的一条通路。 迷宫的表示: 迷宫由 0 和 1 构成的二维数组表示。0 表示可以走的路径,1 表示障碍。用户输入迷宫的…...

多媒体技术的 发展阶段----高中信息技术教资面试
上课,同学们好!请坐 在正式上课之前,老师带来 了一段微课视频,请同学们认真观看大屏幕。等下来回答老师的问题。 好,视频播放完成了,现在老师想问问大家。大家从视频中都看到了什么尼?好&…...

行为型设计模式之《责任链模式》实践
定义 责任链模式(Chain Of Responsibility Pattern)顾名思义,就是为请求创建一条处理链路,链路上的每个处理器都判断是否可以处理请求,如果不能处理则往后走,依次从链头走到链尾,直到有处理器可…...

中酱黑松露手工古法酱油,邂逅独特 “酱油红”
在美食的世界里,调味品往往扮演着画龙点睛的角色,它们虽不似主食材那般夺目,却能悄无声息地赋予菜肴灵魂与韵味。而今天,要带大家走进的,便是中酱手工古法酱油所营造出的独特美味天地,去领略那一抹别具魅力…...

Java NIO channel
channel(通道),byteBuffer(缓冲区),selector(io多路复用),通道FileChannel,SocketChannel的transferTo,transferFrom,MappedByteBuffer实现了零拷贝。 JVM调操作系统方法,read,write,都可以送字…...

智能交通(8)——腾讯开悟智能交通信号灯调度赛道
本文档用于记录参加腾讯开悟智能信号灯调度赛道的模型优化过程。官方提供了dqn和target_dqn算法,模型的优化在官方提供的代码基础上进行。最终排名是在榜单16,没能进入最后的决赛。 一.赛题介绍 赛题简介:在本地赛题中,参赛团队…...

ip所属地址是什么意思?怎么改ip地址归属地
在数字化时代,IP地址作为网络设备的唯一标识符,不仅关乎设备间的通信,还涉及到用户的网络身份与位置信息。IP所属地址,即IP地址的归属地,通常反映了设备连接互联网时的地理位置。本文将深入解析IP所属地址的含义&#…...

攻防世界 ctf刷题 新手区1-10
unserialize3 因为我上个笔记写了 php返序列化 所以先趁热打铁 看这个题目名字 我们就知道是 反序列化呀 因为flag有值所以 我们先输个 111 看看有没有线索 没线索但是这边 有个发现就是他是使用get方式传参的 可能他会把我们的输入 进行传入后台有可能进行反…...

Node做一个自动删除指定文件和文件夹工具
node14 可以搭配脚手架工具实现自动实现删除 // 引入path模块,用于处理文件路径 const path require(path); // 引入fs模块的promises API,用于异步文件操作 const fs2 require(fs).promises; // 引入fs模块,用于同步文件操作 const fs …...

陈若尧新歌《一来二去》陆续登陆全球音乐平台
由青年演员,歌手陈若尧带来的全新创作单曲《一来二去》由索尼音乐发行,于2024年11月18日陆续全球上线。这也是陈若尧与索尼音乐合作的第一首单曲。探索古典风格与流行音乐的新结合。歌曲上线不久,就因优美抒情的动人旋律,诗意而意味深远的歌词…...

【Docker】针对开发环境、测试环境、生产环境如何编排?
目录 一、引言 二、Docker Compose 文件基础 三、针对不同环境的 Docker 编排 开发环境 测试环境 生产环境 四、配置文件全局变量的编写 五、总结 一、引言 在软件开发和部署的过程中,不同的环境有着不同的需求和配置。Docker 作为一种强大的容器化技术&…...

小程序项目的基本组成结构
分类介绍 项目根目录下的文件及文件夹 pages文件夹 用来存放所有小程序的页面,其中每个页面都由4个基本文件组成,它们分别是: .js文件:页面的脚本文件,用于存放页面的数据、事件处理函数等 .json文件:…...

001-mysql安装
[rootcentos701 ~]# hostname -I 10.0.0.200 172.17.0.1 [rootcentos701 ~]# hostname centos701 [rootcentos701 ~]# rpm -qa | grep mariadb [rootcentos701 ~]# rpm -e --nodeps mariadb-libs-5.5.65-1.el7.x86_64 [rootcentos701 ~]# useradd mysql -s /sbin/nologin #创建…...

预训练模型与ChatGPT:自然语言处理的革新与前景
目录 一、ChatGPT整体背景认知 (一)ChatGPT引起关注的原因 (二)与其他公司的竞争情况 二、NLP学习范式的发展 (一)规则和机器学习时期 (二)基于神经网络的监督学习时期 &…...

高通---Camera调试流程及常见问题分析
文章目录 一、概述二、Camera配置的整体流程三、Camera的代码架构图四、Camera数据流的传递五、camera debug FAQ 一、概述 在调试camera过程中,经常会遇到各种状况,本篇文章对camera调试的流程进行梳理。对常见问题的提供一些解题思路。 二、Camera配…...
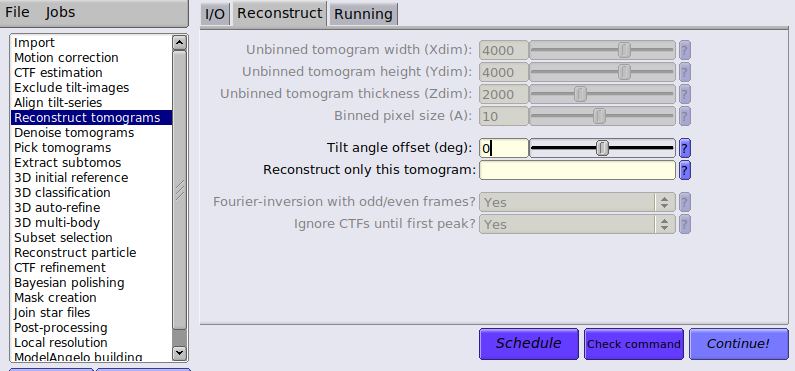
【冷冻电镜】RELION5.0使用教程总结
准备数据集: A test data set composed of 5 tomograms of immature HIV-1 dMACANC VLPs, which is available at EMPIAR-10164. 原始倾斜系列数据需要是单独的影片或单独的运动校正图像,但不是组合倾斜系列堆栈。 mdoc 文件包含每个倾斜系列的元数据。…...

【Maven系列】深入解析 Maven 镜像配置
前言 Maven 是一个流行的 Java 项目管理和构建工具,可以自动化构建项目、管理依赖、生成报告等。在Maven构建项目时,通常经常需要下载各种依赖。默认情况下,Maven 会从中央仓库下载这些依赖,但在某些情况下,这个过程可…...

优质翻译在美国电子游戏推广中的作用
美国作为世界上最大的视频游戏市场之一,为寻求全球成功的游戏开发商提供了无与伦比的机会。然而,美国市场的文化和语言多样性使其成为一个复杂的导航景观。高质量的翻译在弥合开发者和这些充满活力的观众之间的差距方面发挥着关键作用,确保游…...

数据结构---栈(Stack)
1. 简介 栈(Stack)是计算机科学中的一种抽象数据类型,它遵循特定的操作顺序,即后进先出(Last In First Out,LIFO)。这意味着最后添加到栈中的元素将是第一个被移除的。栈的基本操作通常包括&am…...

【全网最新】若依管理系统基于SpringBoot的前后端分离版本开发环境配置
目录 提前准备: 下载源代码 设置依赖 设置后台连接信息 运行后台 运行前端 安装npm依赖 启动前端 登录网页客户端 提前准备: 1、安装mysql 5以上就可以。 2、安装redis. 3、安装npm npm下载地址:https://nodejs.org/dist/v22.12…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
