动态规划<四> 回文串问题(含对应LeetcodeOJ题)
目录
引例
其余经典OJ题
1.第一题
2.第二题
3.第三题
4.第四题
5.第五题
引例
OJ 传送门Leetcode<647>回文子串
画图分析:

使用动态规划解决
原理:能够将所有子串是否是回文的信息保存在dp表中
在使用暴力方法枚举出所有子串,是使用两指针(i,j)依次往后枚举的,且满足i<=j
所以需要建立二维的dp表,在填表时只需填上三角位置即可
1.状态表示:
dp[i][j]表示字符串s的[i,j](i是起始位置,j是结束位置)的这个子串是否是回文
2.状态转移方程

对于线性dp可以采用多画图的方式来分析

3.初始化
因为满足i<=j 并且越界的情况都已经被判断了,是无需做初始化的
4.填表顺序
因为在求dp[i][j]时会用到dp[i+1][j-1]的值,所以填表顺序是整体从下往上,每一行从左往右
5.返回值
返回dp表中true的数量
具体代码
int countSubstrings(string s) {int n=s.size();vector<vector<bool>> dp(n,vector<bool>(n));//创建dp表int ret=0;for(int i=n-1;i>=0;--i)//填表{for(int j=i;j<n;++j)//从i位置开始往后枚举{if(s[i]==s[j]){dp[i][j]=i+1<j? dp[i+1][j-1]:true;}if(dp[i][j]) ++ret;}}return ret;//返回}其余经典OJ题
1.第一题
OJ 传送门Leetcode<5>最长回文子串
画图分析:

使用动态规划解决
对于本道题是计算最长的回文子串,在上面的例题中已经实现了判断字符串的子串是否是回文,只需在dp表中为true的位置找出最长的回文串
其余的参考上面的例题
5.返回值
在dp表中为true的位置找出最长回文串的起始位置i及长度,返回子串
具体代码:
string longestPalindrome(string s) {int n=s.size();vector<vector<bool>> dp(n,vector<bool>(n));int begin=0,len=1;for(int i=n-1;i>=0;--i){for(int j=i;j<n;++j){if(s[i]==s[j]){dp[i][j]=i+1<j? dp[i+1][j-1]:true;}if(dp[i][j] && j-i+1>len){begin=i;len=j-i+1;}}}return s.substr(begin,len);}2.第二题
OJ 传送门Leetcode<1745>分割回文串IV
画图分析:
 使用动态规划来解决
使用动态规划来解决
对于本题是将字符串划分为三子串,只要每个子串是回文串即可
这里可以两下标i,j来划分这个字符串

此时只需要根据上面例题所实现的dp表来逐步划分区间判断
具体代码:
bool checkPartitioning(string s) {int n=s.size();//用dp把所有的子串是否是回文预处理一下vector<vector<bool>> dp(n,vector<bool>(n));for(int i=n-1;i>=0;--i){for(int j=i;j<n;++j){if(s[i]==s[j]){dp[i][j]=i+1<j? dp[i+1][j-1]:true;}}}//枚举所有的第二个子串的起始位置及结束位置for(int i=1;i<n-1;++i){for(int j=i;j<n-1;++j){if(dp[0][i-1] && dp[i][j] && dp[j+1][n-1]) return true;}}return false;}3.第三题
OJ 传送门Leetcode<132>分割回文串II
画图分析:
 使用动态规划来解决
使用动态规划来解决
1.状态表示 ---经验+题目要求
dp[i]表示字符串s.substr(0,i+1)这个子串要分割为回文串的最少分割次数
2.状态转移方程

3.初始化
对于这里的dp表本身在填表时由于j>0是不会访问越界的,但题目求得是最小值
在求dp[i]=min(dp[j-1]+1,dp[i])时,若初始化时都0时,dp[i]=0,是会影响求min的,因此初始化为INT_MAX
4.填表顺序 ------从左往右
5.返回值-------dp[n-1]
具体代码:
int minCut(string s) {//预处理一下int n=s.size();vector<vector<bool>> IsPal(n,vector<bool>(n));for(int i=n-1;i>=0;--i)for(int j=i;j<n;++j)if(s[i]==s[j])IsPal[i][j]=i+1<j? IsPal[i+1][j-1]:true;vector<int> dp(n,INT_MAX); for(int i=0;i<n;++i){if(IsPal[0][i]) dp[i]=0;else{for(int j=1;j<=i;++j)if(IsPal[j][i]) dp[i]=min(dp[j-1]+1,dp[i]);}}return dp[n-1];}4.第四题
OJ 传送门Leetcode<516>最长回文子序列
画图分析:
 使用动态规划解决
使用动态规划解决
1.状态表示
dp[i]表示以i位置为结尾的所有子序列中,最长回文子序列的长度
当使用此状态表示来求解状态转移方程时
当求解dp[i]时,因为此题是子序列,所以需要用到dp[i-1],dp[i-2],....,而dp表中存的只是长度,当在每种结果后添加字符s[i]后,并不能保证是继续是回文串,因此推导不出状态转移方程
这时可以借用上面例题的方法来解决这题

状态表示:
dp[i][j]表示s字符串[i,j]区间内的所有子序列,最长回文子序列的长度
2.状态转移方程

3.初始化
对于本题可以不用初始化,会越界的位置为i==j,而这些位置已经判断过了

4.填表顺序
整体从上往下,每一行从左往右
5.返回值 dp[0][n-1]
具体代码:
int longestPalindromeSubseq(string s) {int n=s.size();vector<vector<int>> dp(n,vector<int>(n));for(int i=n-1;i>=0;--i){for(int j=i;j<n;++j){if(s[i]==s[j]){if(i==j) dp[i][j]=1;else dp[i][j]=dp[i+1][j-1]+2;}elsedp[i][j]=max(dp[i+1][j],dp[i][j-1]);}}return dp[0][n-1];}5.第五题
OJ 传送门Leetcode<1312>让字符串成为回文串的最少插入次数
画图分析:
 使用动态规划解决
使用动态规划解决
1.状态表示 根据经验+题目要求
dp[i][j]表示:s字符串[i,j]区间的子串,让它变为回文串的最小操作次数
2.状态转移方程---认识根据s[i]与s[j]的关系来判断

3.初始化:
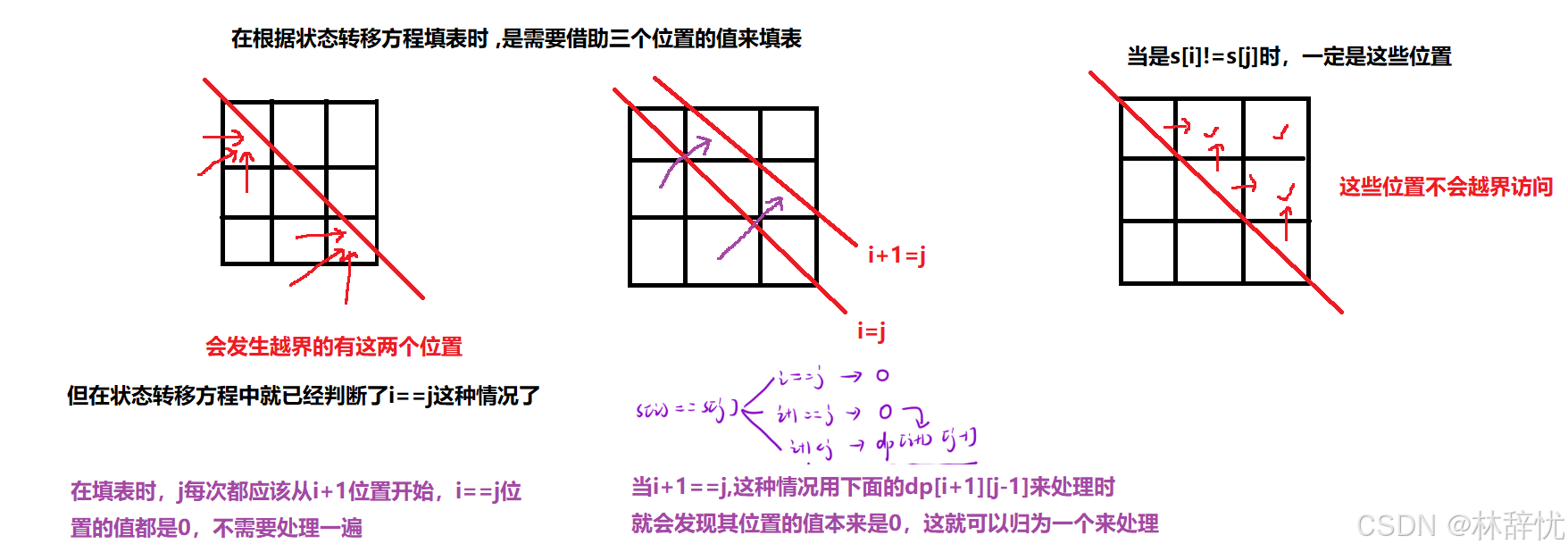
4.填表顺序
整体从下往上,每一行从左往右
5.返回值 dp[0][n-1]
具体代码:
int minInsertions(string s) {int n=s.size();vector<vector<int>> dp(n,vector<int>(n));for(int i=n-1;i>=0;--i){for(int j=i+1;j<n;++j){if(s[i]==s[j]) dp[i][j]=dp[i+1][j-1];else dp[i][j]=min(dp[i][j-1],dp[i+1][j])+1;}}return dp[0][n-1];}相关文章:

动态规划<四> 回文串问题(含对应LeetcodeOJ题)
目录 引例 其余经典OJ题 1.第一题 2.第二题 3.第三题 4.第四题 5.第五题 引例 OJ 传送门Leetcode<647>回文子串 画图分析: 使用动态规划解决 原理:能够将所有子串是否是回文的信息保存在dp表中 在使用暴力方法枚举出所有子串,是…...
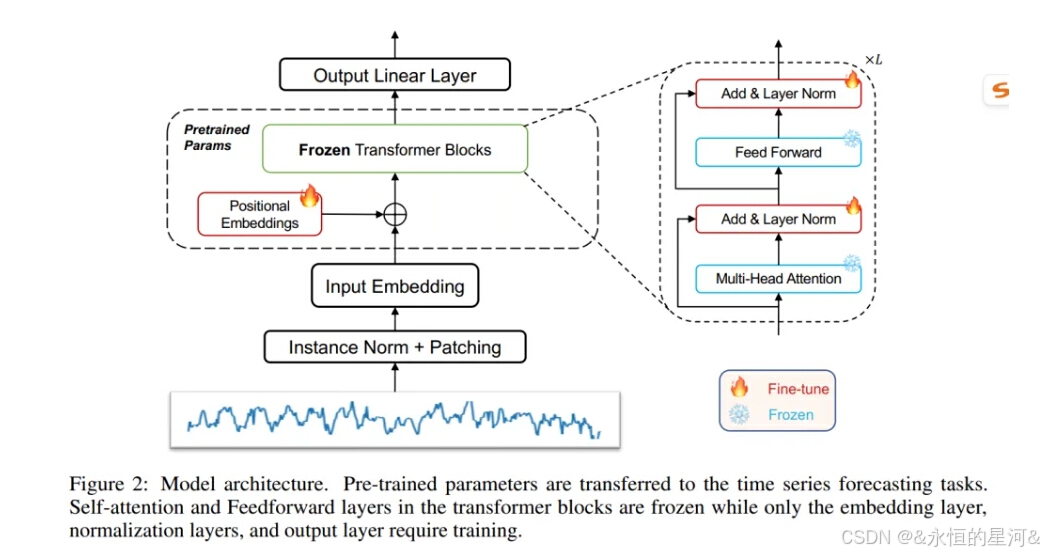
跨模态知识迁移:基于预训练语言模型的时序数据建模
在NLP和CV领域,通常通过在统一的预训练模型上进行微调,能够在各自领域的下游任务中实现SOTA(最先进)的结果。然而,在时序预测领域,由于数据量相对较少,难以训练出一个统一的预训练模型来覆盖所有…...
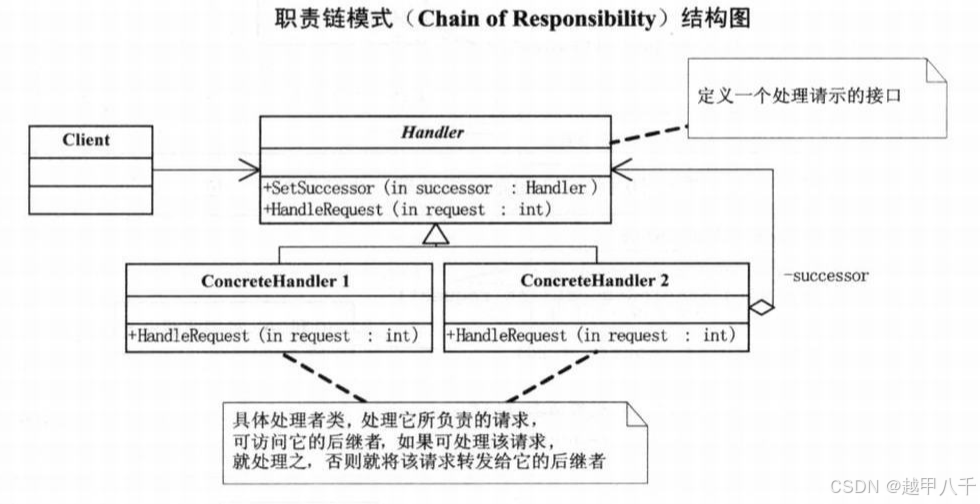
重温设计模式--职责链模式
文章目录 职责链模式的详细介绍C 代码示例C示例代码2 职责链模式的详细介绍 定义与概念 职责链模式(Chain of Responsibility Pattern)是一种行为型设计模式,它旨在将请求的发送者和多个接收者解耦,让多个对象都有机会处理请求&a…...

git冲突解决
git冲突解决 最近遇到了一次git冲突的问题 起因是因为最近公司数据推送部分重构,负责重构的同事就改动了我的一小部分推送的代码,然后等我开发完合并到远程master的时候,报了merge冲突。我对于git工具确实不是很熟练,只是学习了…...
--面向对象编程)
Java学习笔记(14)--面向对象编程
面向对象基础 学习资料来自多态 - Java教程 - 廖雪峰的官方网站 目录 面向对象基础 Override 多态 举个例子 覆写Object方法 调用super final 练习 小结 Override 在继承关系中,子类如果定义了一个与父类方法签名完全相同的方法,被称为覆写&…...

《Swift 字面量》
《Swift 字面量》 介绍 在 Swift 编程语言中,字面量是一种表示源代码中固定值的表达方式。字面量可以直接表示数字、字符串、布尔值等基本数据类型,为编程提供了简洁和直观的方式。Swift 支持多种类型的字面量,包括整数字面量、浮点数字面量…...

数据库 SQL 常用语句全解析
数据库 SQL 常用语句全解析 在数据库领域,SQL(Structured Query Language)作为标准语言,掌控着数据的查询、插入、更新与删除等关键操作。无论是新手入门数据库,还是经验丰富的开发者日常工作,熟练掌握 SQ…...

SQLite 命令
关于《SQLite 命令》的文章,我可以为您概述一些关键点。SQLite是一个轻量级的数据库管理系统,它被广泛用于各种应用程序中。SQLite命令主要分为两类:一类是SQL命令,另一类是SQLite特定的点命令。 SQL命令:这些命令用于…...
本地如何启动casdoor
1、下载代码 GitHub - casdoor/casdoor at v1.777.0 下载对应tag的代码,我这里选择的时v1.777.0版本 通过网盘分享的文件:casdoor-1.777.0.zip 链接: https://pan.baidu.com/s/1fPNqyJYeyfZnem_LtEc0hw 提取码: avpd 2、启动后端 1、使用goland编译…...

目标检测-R-CNN
R-CNN在2014年被提出,算法流程可以概括如下: 候选区域生成:利用选择性搜索(selective search)方法找出图片中可能存在目标的候选区域(region proposal) CNN网络提取特征:对候选区域进行特征提取(可以使用AlexNet、VGG等网络) 目…...

【持续更新】Github实用命令
Intro 最近高强度使用github,遂小计于此作为备忘。 Basic github是一个代码管理软件,能够track文件变动并且管理版本,是当代coding必不可少的工具。当你安装好github在本地以后,你可以通过以下命令初始化当前文件夹(…...

docker 容器的基本使用
docker 容器 一、docker是什么? 软件的打包技术,就是将算乱的多个文件打包为一个整体,打包技术在没有docker容器之前,一直是有这种需求的,比如上节课我把我安装的虚拟机给你们打包了,前面的这种打包方式是…...

css让按钮放在最右侧
要将 el-button 按钮放在最右侧,可以使用多种方法,具体取决于使用的布局方式和样式库。以下是几种常见的解决方案: 方法 1:使用 CSS Flexbox Flexbox 是一种非常灵活的布局方式,可以轻松实现水平或垂直对齐。你可以将…...
8K+Red+Raw+ProRes422分享5个影视级视频素材网站
Hello,大家好,我是后期圈! 在视频创作中,电影级的视频素材能够为作品增添专业质感,让画面更具冲击力。无论是广告、电影短片,还是品牌宣传,高质量的视频素材都是不可或缺的资源。然而ÿ…...

Linux网络——UDP的运用
Linux网络——UDP的运用 文章目录 Linux网络——UDP的运用一、引入二、服务端实现2.1 创建socket套接字2.2 指定网络接口并bind2.3 接收数据并处理2.4 整体代码2.5 IP的绑定的细节 三、用户端实现3.1 创建套接字3.2 指定网络接口3.3 发生数据并接收3.4 绑定问题 四、代码五、UD…...

项目亮点案例
其实对我来说是日常操作,但是如果在面试的时候面试者能把日常的事情总结好发出来,其实足矣。 想让别人认同项目,选取的示例需要包含以下要素: 亮点项目四要素:明确的目标,问题点,解决方法和结果…...

Retrofit源码分析:动态代理获取Api接口实例,解析注解生成request,线程切换
目录 一,Retrofit的基本使用 1.定义api接口 2.创建Retrofit实例 3.获取api接口实例发起请求 二,静态代理和动态代理 1,静态代理 2,动态代理 三,动态代理获取Api接口实例 四,解析接口方法注解&…...

范德蒙矩阵(Vandermonde 矩阵)简介:意义、用途及编程应用
参考: Introduction to Applied Linear Algebra – Vectors, Matrices, and Least Squares Stephen Boyd and Lieven Vandenberghe 书的网站: https://web.stanford.edu/~boyd/vmls/ Vandermonde 矩阵简介:意义、用途及编程应用 在数学和计算科学中&a…...

【中标麒麟服务器操作系统实例分享】java应用DNS解析异常分析及处理
了解更多银河麒麟操作系统全新产品,请点击访问 麒麟软件产品专区:https://product.kylinos.cn 开发者专区:https://developer.kylinos.cn 文档中心:https://document.kylinos.cn 情况描述 中标麒麟服务器操作系统V7运行在 ARM…...

网安瞭望台第17期:Rockstar 2FA 故障催生 FlowerStorm 钓鱼即服务扩张现象剖析
国内外要闻 Rockstar 2FA 故障催生 FlowerStorm 钓鱼即服务扩张现象剖析 在网络安全的复杂战场中,近期出现了一个值得关注的动态:名为 Rockstar 2FA 的钓鱼即服务(PhaaS)工具包遭遇变故,意外推动了另一个新生服务 Flo…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
