1919C. Grouping Increases
问题描述
序列 X X X,划分成两个字序列 A , B A,B A,B,其中惩罚是 A , B A,B A,B之中, A [ i ] < A [ i + 1 ] , B [ i ] < B [ i + 1 ] A[i] < A[i+1], B[i] < B[i+1] A[i]<A[i+1],B[i]<B[i+1]的个数
思路
-
拆分 X X X,实际上是个在线的过程,不断的从 X X X中拿数字往 A , B A,B A,B之中填。
-
我们假设 A , B A,B A,B的最后一个数字为 A l , B l A_l,B_l Al,Bl, 针对元素 X [ i ] X[i] X[i]的插入,下列三种情况进行不同的讨论,不失一般性,我们假设 A l < = B l A_l <= B_l Al<=Bl。
情况1: X [ i ] < = A l X[i] <= A_l X[i]<=Al
添 X [ i ] X[i] X[i]到 A A A里,因为 B l B_l Bl可接受的范围一定更广泛情况2: X [ i ] > B l X[i] > B_l X[i]>Bl
添 X [ i ] X[i] X[i]到 A A A里,因为添加到 B B B的末尾,会损失一个大一点的数字情况3: A l < X [ i ] < = B l A_l < X[i] <= B_l Al<X[i]<=Bl
添 X [ i ] X[i] X[i]到 B B B里,不论到A和B得会到一个负分,该决策优于添加到A,这个在文末证明。
代码
void solve()
{int n;cin >> n;vector<int> v(n + 1);for (int i = 1; i <= n; i++){cin >> v[i];}int a, b;a = b = INT_MAX;int penalty = 0;for (int i = 1; i <= n; i++){if (a > b) // a <= b{swap(a, b);}if (v[i] <= a){a = v[i];}else if (v[i] <= b){b = v[i];}else{penalty++;a = v[i];}}cout << penalty << "\n";
}
证明
情况3我们可以比较两种决策,
决策1:插入A
决策2:插入B
决策2的收益来的比较短,比如下面这种场景
A : [ 3 ] A:[3] A:[3]
B : [ 8 ] B:[8] B:[8]
X [ i ] = 5 X[i] = 5 X[i]=5
A : [ 3 ] A:[3] A:[3]
B : [ 8 , 5 ] B:[8, 5] B:[8,5]
如果我们下一个数字 X [ i + 1 ] X[i+1] X[i+1]为7,就得到1点负面收益
A : [ 3 , 7 ] A:[3, 7] A:[3,7]
B : [ 8 , 5 ] B:[8, 5] B:[8,5]
决策1的收益在与后期,比如:
A : [ 3 ] A:[3] A:[3]
B : [ 8 ] B:[8] B:[8]
X [ i ] = 5 X[i] = 5 X[i]=5
A : [ 3 , 5 ] A:[3, 5] A:[3,5]
B : [ 8 ] B:[8] B:[8]
如果我们下一个数字 X [ i + 1 ] X[i+1] X[i+1]为7,那么我们决策1就会得到收益
A : [ 3 , 5 ] A:[3,5] A:[3,5]
B : [ 8 , 7 ] B:[8, 7] B:[8,7]
但是如果我们下个数字大于8, 或者小于等于5,我们决策2和决策1会等价,并且决策2会少一点penalty。
比较上面情况, 决策2全方面的大于决策1
证毕
其实可以通过直觉得到结论,因为如果保留 B l B_l Bl,添加到 A A A里,由于每个数字都只受相邻影响,所以 B l B_l Bl的收最多就1。
相关文章:

1919C. Grouping Increases
问题描述 序列 X X X,划分成两个字序列 A , B A,B A,B,其中惩罚是 A , B A,B A,B之中, A [ i ] < A [ i 1 ] , B [ i ] < B [ i 1 ] A[i] < A[i1], B[i] < B[i1] A[i]<A[i1],B[i]<B[i1]的个数 思路 拆分 X X X…...

Pion WebRTC 项目教程
Pion WebRTC 项目教程 webrtc Pure Go implementation of the WebRTC API [这里是图片001] 项目地址: https://gitcode.com/gh_mirrors/we/webrtc 1. 项目目录结构及介绍 Pion WebRTC 项目的目录结构如下: pion/webrtc ├── api ├── examples ├── inter…...

【安全编码】Web平台如何设计防止重放攻击
我们先来做一道关于防重放的题,答案在文末 防止重放攻击最有效的方法是( )。 A.对用户密码进行加密存储使用 B.使用一次一密的加密方式 C.强制用户经常修改用户密码 D.强制用户设置复杂度高的密码 如果这道题目自己拿不准,或者…...

VUE3+django接口自动化部署平台部署说明文档(使用说明,需要私信)
网址连接:http://118.25.110.213:5200/#/login 账号/密码:renxiaoyong 1、VUE3部署本地。 1.1本地安装部署node.js 1.2安装vue脚手架 npm install -g vue/cli # 或者 yarn global add vue/cli1.3创建本地项目 vue create my-vue-project1.4安装依赖和插…...
)
Python爬虫(入门+进阶)
简介 围绕 Python 爬虫展开,包括四个章节。第一章从 Python 爬虫入门,涵盖爬虫概念、Requests 爬取、Xpath 解析、数据保存及入库等知识,并结合知乎、豆瓣、淘宝等案例讲解浏览器抓包及 Selenium 爬取动态网页。第二章介绍 Scrapy 框架&…...
保姆级教程Docker部署RabbitMQ镜像
目录 1、安装Docker及可视化工具 2、创建挂载目录 3、运行RabbitMQ容器 4、Compose运行RabbitMQ容器 5、开启界面插件 6、查看RabbitMQ运行状态 7、常见问题处理 1、安装Docker及可视化工具 Docker及可视化工具的安装可参考:Ubuntu上安装 Docker及可视化管理…...

【RAII | 设计模式】C++智能指针,内存管理与设计模式
前言 nav2系列教材,yolov11部署,系统迁移教程我会放到年后一起更新,最近年末手头事情多,还请大家多多谅解。 上一节我们讲述了C移动语义相关的知识,本期我们来看看C中常用的几种智能指针,并看看他们在设计模式中的运…...

Linux复习3——管理文件系统2
修改文件权限命令 chmod 功能: chmod 命令主要用于修改文件或者目录的权限 只有文件所有者和超级用户可以修改文件或目录的权限 (1)使用数字表示法修改权限 所谓数字表示法是指将读取(r)、写入(w)和执行(x)分别以4、2、1来表示,没有授予的部分就表示…...

c++---------数据类型
基本数据类型 整数类型(Integral Types) int(整型) 这是最常用的整数类型,通常用于存储一般范围的整数值。在32位系统中,int类型一般占用4个字节,取值范围大约是 - 2147483648到2147483647。例如…...
Django vs Flask:哪种框架适合构建你的下一个Web应用?)
前端Python应用指南(三)Django vs Flask:哪种框架适合构建你的下一个Web应用?
《写给前端的python应用指南》系列: (一)快速构建 Web 服务器 - Flask vs Node.js 对比(二)深入Flask:理解Flask的应用结构与模块化设计 在上一篇博文中,我们深入探讨了Flask框架,…...
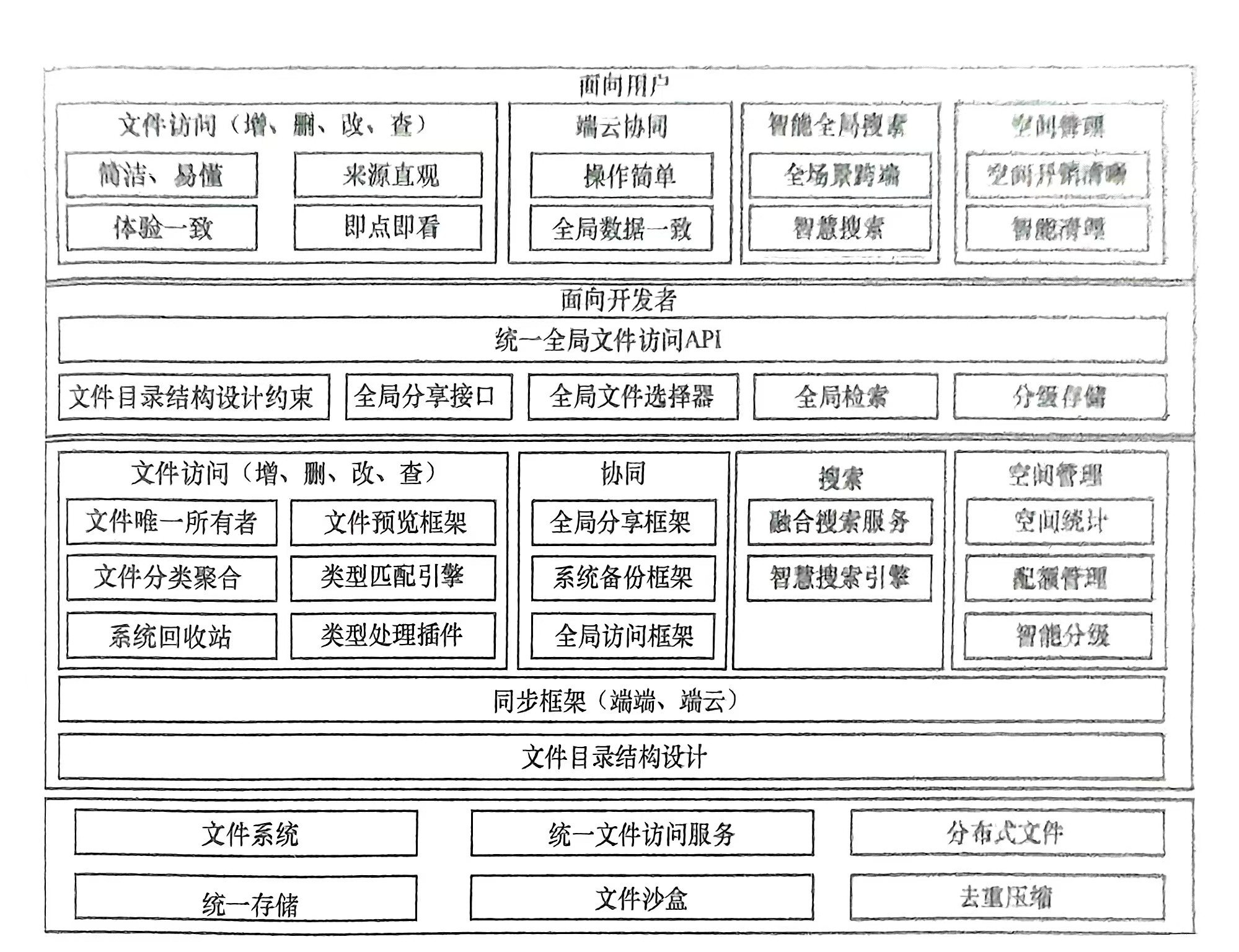
鸿蒙系统文件管理基础服务的设计背景和设计目标
有一定经验的开发者通常对文件管理相关的api应用或者底层逻辑都比较熟悉,但是关于文件管理服务的设计背景和设计目标可能了解得不那么清楚,本文旨在分享文件管理服务的设计背景及目标,方便广大开发者更好地理解鸿蒙系统文件管理服务。 1 鸿蒙…...

要查询 `user` 表中 `we_chat_open_id` 列不为空的用户数量
要查询 user 表中 we_chat_open_id 列不为空的用户数量,你可以使用以下 SQL 查询语句: SELECT COUNT(*) FROM user WHERE we_chat_open_id IS NOT NULL AND we_chat_open_id ! ;解释: SELECT COUNT(*): 表示要计算符合条件的行数。FROM us…...

AI科研助手开发总结:向量与数据权限的应用(二)
一、前言 继上篇文章:AI科研助手开发总结:向量与数据权限的应用(一) 本章根据向量库内存储数据及权限,向量库统一维护和管理数据权限方案讨论。 二、方案分析-基于向量Fields 2.1 思路 结合橙语AI科研助手的业务场…...

python爬虫----爬取视频实战
python爬虫-爬取视频 本次爬取,还是运用的是requests方法 首先进入此网站中,选取你想要爬取的视频,进入视频页面,按F12,将网络中的名称栏向上拉找到第一个并点击,可以在标头中,找到后续我们想要…...

HarmonyOS NEXT 实战之元服务:静态案例效果--航空出行
背景: 前几篇学习了元服务,后面几期就让我们开发简单的元服务吧,里面丰富的内容大家自己加,本期案例 仅供参考 先上本期效果图 ,里面图片自行替换 效果图1完整代码案例如下: import { authentication } …...

DP83848以太网移植流程,可以TCP通信
DP83848-EP 是一款高度可靠、功能丰富的强大器件,包含了增强型 ESD 保护、MII 和 RMII,从而在 MPU 选择方面实现最大的灵活性,所有这些特性都融入于 48 引脚 PQFP 封装中。 DP83848-EP 配备 集成子层以支持 10BASE-T 和 100BASE-TX 以太网协议,这些协议确保了与基于其他标…...

css 裁剪 clip-path
clip-path 是一个强大的 CSS 属性,用于裁剪元素的可视区域,支持多种形状裁剪。它可以用来创建复杂的裁剪效果,如圆形、多边形、路径等。 clip-path: none | shape | url(#clipPathId);none:不裁剪,显示完整内容。shap…...

MySQL用表组织数据
用表组织数据 文章目录 用表组织数据一.四种完整性约束二.数值类型2-1三.数值类型2-2四.字符串.日期类型五.设置1.设置主键2.设置标识列3.设置非空4.设置默认值 六.主外键建立后注意事项 一.四种完整性约束 1.域完整性 列 域完整性约束方法:限制数据类型,检查约束,外键约束,默…...

细说STM32F407单片机轮询方式读写SPI FLASH W25Q16BV
目录 一、工程配置 1、时钟、DEBUG 2、GPIO 3、SPI2 4、USART6 5、NVIC 二、软件设计 1、FALSH (1)w25flash.h (2) w25flash.c 1)W25Q16基本操作指令 2)计算地址的辅助功能函数 3)器…...

C++-------指针
把地址当做数值 在 C 中,指针本质上就是存储内存地址的变量。每个变量在内存中都有一个唯一的地址,通过取地址运算符 & 可以获取变量的地址,这个地址本质上是一个整数(在 32 位系统中是 32 位整数,64 位系统中是 …...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
