金属衬底介质片对平面波的反射-问题的解析求解和FEM求解
金属衬底介质片对平面波的反射-问题的解析求解和FEM求解
参考有限元从零单排系列4
代码参考了上面大佬文章提供的,但是部分计算系数错了,我改了下加了许多注释,便于大家理解。
书籍参考的电磁场有限元方法(金建铭),所用的公式都是这本书的。
下载地址:金属衬底介质片对平面波的反射-问题的解析求解和FEM求解-MATLAB代码
QAQ
QAQ
QAQ
0、问题定义
一个均匀平面波斜入射从自由空间入射到电介质中,电介质中的 ε r \varepsilon_{r} εr和 μ r \mu_{r} μr随着其深度 L L L而变化,电介质材料的衬底为理想金属PEC。
入射波沿着 θ \theta θ角入射,并发生反射,我们需要求解其反射系数。
其中介电常数是非均匀的,其表达式为:
ϵ r = 4 + ( 2 I − j 0.1 ) ( 1 − x / L ) 2 \epsilon^{\mathrm{r}}=4+(2^{\mathrm{I}}-\mathrm{j}0.1)(1-x/L)^{2} ϵr=4+(2I−j0.1)(1−x/L)2
磁导率为固定的复数:
μ r = 2 − j 0.1 \mu_{\mathrm{r}}=2-\mathrm{j}0.1 μr=2−j0.1
介质板的厚度为5个波长:
L = 5 λ L=5 {\lambda} L=5λ

1、解析求解方法
2、FEM求解方法
2.1、FEM求解目标方程
任意电磁平面波都能分解成只有 E z E_{z} Ez分量的电场极化波和只有 H z H_{z} Hz分量的磁场极化波,因此这个问题只需要分别考虑这两种情况即可。对于极化波,入射波的电场强度 E z E_{z} Ez表达式为(金-式3.81):
E z i n c ( x , y ) = E 0 e j k 0 x cos θ − j k 0 y sin θ E_{z}^{\mathrm{inc}}(x,y)=E_{0}\mathrm{e}^{\mathrm{j}k_{0}x\cos\theta-\mathrm{j}k_{0}y\sin\theta} Ezinc(x,y)=E0ejk0xcosθ−jk0ysinθ
其中 E 0 {E_{0}} E0为入射场大小。
此处实际要求解方程为(金-式3.82):
d d x ( 1 μ r d E z d x ) + k 0 2 ( ϵ r − 1 μ r sin 2 θ ) E z = 0 {\frac{\mathrm{d}}{\mathrm{d}x}}\left({\frac{1}{\mu_{\mathrm{r}}}}{\frac{\mathrm{d}E_{z}}{\mathrm{d}x}}\right)+k_{0}^{2}\left(\epsilon_{\mathrm{r}}-{\frac{1}{\mu_{\mathrm{r}}}}\sin^{2}\theta\right)E_{z}=0 dxd(μr1dxdEz)+k02(ϵr−μr1sin2θ)Ez=0
推导得到的边界条件为:
[ d E z d x + j k 0 cos θ E z ( x ) ] x = L + 0 = 2 j k 0 cos θ E 0 e j k 0 L cos θ \left[{\frac{\mathrm{d}E_{z}}{\mathrm{d}x}}+\mathrm{j}k_{0}\cos\theta E_{z}(x)\right]_{x=L+0}=2\mathrm{j}k_{0}\cos\theta E_{0}\mathrm{e}^{\mathrm{j}k_{0}L\cos\theta} [dxdEz+jk0cosθEz(x)]x=L+0=2jk0cosθE0ejk0Lcosθ
2.2、FEM求解Matlab编程
2.2.1 基础参数定义
- 定义波长,随意设置对最终结果没有影响
- 自由空间波数计算公式
- 基板的厚度为5倍波长-这是给定的条件
- 有限元剖分-100个单元
- 单元节点坐标x1到xm
- 求解对应角度下的反射数据
- E0为入射场大小,对反射计算结果无影响
%基本物理参数
lambda=1;%定义波长,随意设置对最终结果没有影响
k0=2*pi/lambda;%自由空间波数计算公式
L=5*lambda;%基板的厚度为5倍波长-这是给定的条件
element_num=100;%有限元剖分-100个单元
x=linspace(0,L,element_num+1);%单元节点坐标x1到xm
theta=linspace(0,pi/2,20);%求解对应角度下的反射数据
% theta=[0,pi/4];%求解45度下的反射数据
E0=1;%E0为入射场大小,对反射计算结果无影响
2.2.2 材料信息定义
依旧题目条件定义的材料信息如下所示:
- 介质板内材料的非均匀介电常数
- 介质板外自由空间介电常数
- 介质板内材料的磁导率
- 介质板外自由空间磁导率
%材料参数
epsilon_r=4+(2-0.1*1j)*(1-x/L).^2;%介质板内材料的非均匀介电常数
epsilon_r(element_num+1)=1;%介质板外自由空间介电常数
mu_r=ones(1,length(epsilon_r))*(2-0.1j);%介质板内材料的磁导率
mu_r(element_num+1)=1;%介质板外自由空间磁导率
2.2.3 FEM节点信息定义
下面需要定义fem节点信息,其实际上是个结构体,主要包含下面信息:

其中:
- M为节点的标记,若使用100个单元,则M的范围为1-100
- alpha为(金-式3.1)中的 α \alpha α(如下所示),也就是求解的通用微分方程的已知系数
- beta为(金-式3.1)中的 β \beta β(如下所示),也就是求解的通用微分方程的已知系数
- f为(金-式3.1)中的 f f f(如下所示),也就是求解的通用微分方程的激励项
- l是有限元节点之间的距离
alpha、 beta、f对应(金-式3.1)
− d d x ( α d ϕ d x ) + β ϕ = f 0 < x < L -{\frac{\mathrm{d}}{\mathrm{d}x}}\left(\alpha{\frac{\mathrm{d}\phi}{\mathrm{d}x}}\right)+\beta\phi=f\quad0<x<L −dxd(αdxdϕ)+βϕ=f0<x<L
代码:
%存放fem的所有节点信息(结构体信息)
fems=[];
%存放计算得到的反射系数信息
plotData=[];
2.2.4 节点数组赋值
代码如下:
fems=[];%清空fems节点数组
% fem节点数组赋值,并和fems合并为全局节点数组
for j=1:length(x)-1str=['fem',num2str(j),'=inputElementData(j,1/mu_r(j),-k0^2*(epsilon_r(j)-1/mu_r(j)*sin(theta(i))^2),0,x(j),x(j+1));'];eval(str);str2=['fems=[fems;fem',num2str(j),'];'];eval(str2);
end
其中inputElementData函数主要给每个fem节点赋值:
%% 生成单个有限元单元的元胞(单元编号,alpha,beta,f,单元区间)
function fem=inputElementData(M,alpha,beta,f,x1,x2)fem.M=M;fem.alpha=alpha;fem.beta=beta;fem.f=f;fem.l=x2-x1;
end
对比下面两个方程,alpha、beta、f的表达式非常清楚了,可以看到和代码完全对应(金-式3.1和式3.82):
− d d x ( α d ϕ d x ) + β ϕ = f 0 < x < L -{\frac{\mathrm{d}}{\mathrm{d}x}}\left(\alpha{\frac{\mathrm{d}\phi}{\mathrm{d}x}}\right)+\beta\phi=f\quad0<x<L −dxd(αdxdϕ)+βϕ=f0<x<L
d d x ( 1 μ r d E z d x ) + k 0 2 ( ϵ r − 1 μ r sin 2 θ ) E z = 0 {\frac{\mathrm{d}}{\mathrm{d}x}}\left({\frac{1}{\mu_{\mathrm{r}}}}{\frac{\mathrm{d}E_{z}}{\mathrm{d}x}}\right)+k_{0}^{2}\left(\epsilon_{\mathrm{r}}-{\frac{1}{\mu_{\mathrm{r}}}}\sin^{2}\theta\right)E_{z}=0 dxd(μr1dxdEz)+k02(ϵr−μr1sin2θ)Ez=0
2.2.5 初始化边界条件
先给出代码,解释如下:
boundary1=inputBoundaryData('d','min',0);
boundary2=inputBoundaryData('n','max',1j*k0*cos(theta(i)),2j*k0*cos(theta(i))*E0*exp(1j*k0*L*cos(theta(i))));
其中:
%% 边界条件,d为狄利克雷,n为纽曼
function boundaryContent=inputBoundaryData(type,value,varargin)if type == 'd'boundaryContent.type=type;boundaryContent.value=value;boundaryContent.p=varargin{1};boundaryContent.gamma=0;boundaryContent.q=0;elseif type == 'n'boundaryContent.type=type;boundaryContent.value=value;boundaryContent.p=0;boundaryContent.gamma=varargin{1};boundaryContent.q=varargin{2};elseerror('unknown boundary condition!');end
end
显而易见,我们求解的是电场,最左侧(即x轴最小min处)是PEC边界,对应的电场强度为0,因此左侧边界设置为狄利克雷边界(金-式3.2):
inputBoundaryData('d','min',0)
最右侧(即x轴最大max处)是纽曼边界(金-式3.3和式3.94),对比下面两个式子(此问题的边界条件和标准式3.3的格式),gamma和q的值也非常显而易见,这也和上面的编程实现一致:
[ α d ϕ d x + γ ϕ ] x = L = q \left[\alpha{\frac{\mathrm{d}\phi}{\mathrm{d}x}}+\gamma\phi\right]_{x=L}=q [αdxdϕ+γϕ]x=L=q
[ d E z d x + j k 0 cos θ E z ( x ) ] x = L + 0 = 2 j k 0 cos θ E 0 e j k 0 L cos θ \left[{\frac{\mathrm{d}E_{z}}{\mathrm{d}x}}+\mathrm{j}k_{0}\cos\theta E_{z}(x)\right]_{x=L+0}=2\mathrm{j}k_{0}\cos\theta E_{0}\mathrm{e}^{\mathrm{j}k_{0}L\cos\theta} [dxdEz+jk0cosθEz(x)]x=L+0=2jk0cosθE0ejk0Lcosθ
2.2.6 依据FEM节点生成求解矩阵
(金-式3.38)附近,实际的求解的矩阵如下所示:
[ K ] { ϕ } = { b } [K]\{\phi\}=\{b\} [K]{ϕ}={b}
K = [ K 11 ( 1 ) K 12 ( 1 ) 0 0 K 21 ( 1 ) K 22 ( 1 ) + K 11 ( 2 ) K 12 ( 2 ) 0 0 K 21 ( 2 ) K 22 ( 2 ) + K 11 ( 3 ) K 12 ( 3 ) 0 0 K 21 ( 3 ) K 22 ( 3 ) ] K=\begin{bmatrix}K_{11}^{(1)}&K_{12}^{(1)}&0&0\\K_{21}^{(1)}&K_{22}^{(1)}+K_{11}^{(2)}&K_{12}^{(2)}&0\\0&K_{21}^{(2)}&K_{22}^{(2)}+K_{11}^{(3)}&K_{12}^{(3)}\\0&0&K_{21}^{(3)}&K_{22}^{(3)}\end{bmatrix} K= K11(1)K21(1)00K12(1)K22(1)+K11(2)K21(2)00K12(2)K22(2)+K11(3)K21(3)00K12(3)K22(3)
{ b } = { b 1 ( 1 ) b 2 ( 1 ) + b 1 ( 2 ) b 2 ( 2 ) + b 1 ( 3 ) b 2 ( 3 ) } \left.\{b\}=\left\{\begin{array}{c}{b_{1}^{(1)}}\\{b_{2}^{(1)}+b_{1}^{(2)}}\\{b_{2}^{(2)}+b_{1}^{(3)}}\\{b_{2}^{(3)}}\\\end{array}\right.\right\} {b}=⎩ ⎨ ⎧b1(1)b2(1)+b1(2)b2(2)+b1(3)b2(3)⎭ ⎬ ⎫
[a,b,c]=createMatrixElements(fems);
基于上面给出的矩阵,我们下一步是计算其中的元素,计算公式如下(金-式3.28~3.30):
K 11 e = K 22 e = α e l e + β e l e 3 K 12 e = K 21 e = − α e l e + β e l e 6 b 1 e = b 2 e = f e l e 2 \begin{aligned}&K_{11}^{e}=K_{22}^{e}=\frac{\alpha^{e}}{l^{e}}+\beta^{e}\frac{l^{e}}{3}\\&K_{12}^{e}=K_{21}^{e}=-\frac{\alpha^{e}}{l^{e}}+\beta^{e}\frac{l^{e}}{6}\\&b_{1}^{e}=b_{2}^{e}=f^{e}\frac{l^{e}}{2}\end{aligned} K11e=K22e=leαe+βe3leK12e=K21e=−leαe+βe6leb1e=b2e=fe2le
由此写出的代码如下(其中a为对角上的元素值,c为次对角元素的值,b就对应上面的非齐次项):
%% data里面是元胞数组,每个元胞里面都有 alpha,beta,f和l
function [a,b,c]=createMatrixElements(data)sizes=size(data); num=sizes(1);%有限元单元数eleNum=num+1;%有限元单元数+1为节点数%% 生成K矩阵对角元,非对角元和非齐次项的过程a=zeros(eleNum,1);b=zeros(eleNum,1);c=zeros(num,1);a(1)=data(1).alpha/data(1).l+data(1).beta*data(1).l/3;%对角元第一个的公式3.28a(eleNum)=data(num).alpha/data(num).l+data(num).beta*data(num).l/3;%对角元最后一个的公式c(1)=-data(1).alpha/data(1).l+data(1).beta*data(1).l/6;%次对角线第一个的公式3.29b(1)=data(1).f*data(1).l/2; %非齐次项第一项-f为已知的源或者激励b(eleNum)=data(num).f*data(num).l/2; %非齐次项最后一项3.30for j=2:eleNum-1a(j)=data(j-1).alpha/data(j-1).l+data(j-1).beta*data(j-1).l/3+data(j).alpha/data(j).l+data(j).beta*data(j).l/3;%中间的公式3.38b(j)=data(j-1).f*data(j-1).l/2+data(j).f*data(j).l/2;%非齐次项剩余项3.41c(j)=-data(j).alpha/data(j).l+data(j).beta*data(j).l/6;%非对角元的公式3.29end
end
2.2.7 强加边界条件
加入边界条件会对上面的k矩阵和b矩阵进行修正,主要在下面代码进行:
[K,b]=createMatrixK([boundary1,boundary2],a,b,c);%强加边界条件
在此函数中,先把之前的abc数组组合成实际的k矩阵:
sizes=size(a);
num=sizes(1);
K=zeros(num);
for j=1:numK(j,j)=a(j);
end
for j=1:num-1K(j,j+1)=c(j);K(j+1,j)=c(j);
end
对于狄利克雷边界条件,实际的代码会根据下式进行修正(金-式3.62):
[ 1 0 0 0 0 K 22 K 23 K 24 0 K 32 K 33 K 34 0 K 42 K 43 K 44 ] { ϕ 1 ϕ 2 ϕ 3 ϕ 4 } = { p b 2 − K 21 p b 3 − K 31 p b 4 − K 41 p } \left.\left[\begin{array}{cccc}1&0&0&0\\0&K_{22}&K_{23}&K_{24}\\0&K_{32}&K_{33}&K_{34}\\0&K_{42}&K_{43}&K_{44}\end{array}\right.\right]\begin{Bmatrix}\phi_1\\\phi_2\\\phi_3\\\phi_4\end{Bmatrix}=\begin{Bmatrix}p\\b_2-K_{21}p\\b_3-K_{31}p\\b_4-K_{41}p\end{Bmatrix} 10000K22K32K420K23K33K430K24K34K44 ⎩ ⎨ ⎧ϕ1ϕ2ϕ3ϕ4⎭ ⎬ ⎫=⎩ ⎨ ⎧pb2−K21pb3−K31pb4−K41p⎭ ⎬ ⎫
%% 狄利克雷边界条件
if boundaryCondition1.type=='d'K(1,1)=1;b(1)=boundaryCondition1.p;for j=2:numK(1,j)=0;b(j)=b(j)-b(1)*K(j,1);K(j,1)=0;end
end
对于纽曼边界条件,原方程组使用下式进行修正(只在边界上对应的元素进行修正)(金-式3.58~3.59):
K N N = α ( M ) l ( M ) + β ( M ) l ( M ) 3 + γ K_{NN}=\frac{\alpha^{(M)}}{l^{(M)}}+\beta^{(M)}\frac{l^{(M)}}{3}+\gamma KNN=l(M)α(M)+β(M)3l(M)+γ
b N = f ( M ) l ( M ) 2 + q b_{N}=f^{(M)}\frac{l^{(M)}}{2}+q bN=f(M)2l(M)+q
%% 纽曼边界条件
if boundaryCondition2.type=='n'K(num,num)=K(num,num)+boundaryCondition2.gamma;b(num)=b(num)+boundaryCondition2.q;
end
2.2.8 方程组求解
还在等什么,线性方程组不会求解嘛,此处用高斯消元法求解:
results=solveWithGuassianMethod(K,b);%高斯消元法求解
function results=solveWithGuassianMethod(K,b)%生成a和c向量sizes=size(K);num=sizes(1);a=zeros(num,1);c=zeros(num-1,1);for j=1:numa(j)=K(j,j);endfor j=1:num-1c(j)=K(j,j+1);endfor j=2:numa(j)=a(j)-c(j-1)^2/a(j-1);b(j)=b(j)-b(j-1)*c(j-1)/a(j-1);endresults=zeros(num,1);results(num)=b(num)/a(num);for j=num-1:-1:1results(j)=(b(j)-c(j)*results(j+1))/a(j);end
end
2.2.9 求解反射系数
反射系数就是下面的R(金-式3.94):
E z ( x ) = E 0 e j k 0 x cos θ + R E 0 e − j k 0 x cos θ x > L E_{z}(x)=E_{0}\mathrm{e}^{\mathrm{j}k_{0}x\cos\theta}+RE_{0}\mathrm{e}^{-\mathrm{j}k_{0}x\cos\theta}\quad x>L Ez(x)=E0ejk0xcosθ+RE0e−jk0xcosθx>L
我们求解得到results的是在各个节点的电场强度,将位于介质与空气交界处的电场强度带入上式中计算,即可得到反射系数,公式如下:
R=(results(element_num+1)-E0*exp(1j*k0*L*cos(theta(i))))/E0*exp(-1j*k0*L*cos(theta(i)));
2.3 求解结果
杠杠的:
plot(plotData(:,1)*180/pi,abs(plotData(:,2)))

2.4 主函数代码
其余从最上面链接下载吧:
%非均匀金属衬底反射问题有限元解法
clear all;
clc;
%基本物理参数
lambda=1;%定义波长,随意设置对最终结果没有影响
k0=2*pi/lambda;%自由空间波数计算公式
L=5*lambda;%基板的厚度为5倍波长-这是给定的条件
element_num=100;%有限元剖分-100个单元
x=linspace(0,L,element_num+1);%单元节点坐标x1到xm
theta=linspace(0,pi/2,20);%求解对应角度下的反射数据
% theta=[0,pi/4];%求解45度下的反射数据
E0=1;%E0为入射场大小,对反射计算结果无影响
%材料参数
epsilon_r=4+(2-0.1*1j)*(1-x/L).^2;%介质板内材料的非均匀介电常数
epsilon_r(element_num+1)=1;%介质板外自由空间介电常数
mu_r=ones(1,length(epsilon_r))*(2-0.1j);%介质板内材料的磁导率
mu_r(element_num+1)=1;%介质板外自由空间磁导率%存放fem的节点信息(结构体信息)
fems=[];
%存放计算得到的反射系数信息
plotData=[];for i=1:length(theta)%对每个theta进行一次有限元求解fems=[];%清空fems节点数组% fem节点数组赋值,并和fems合并为全局节点数组for j=1:length(x)-1str=['fem',num2str(j),'=inputElementData(j,1/mu_r(j),-k0^2*(epsilon_r(j)-1/mu_r(j)*sin(theta(i))^2),0,x(j),x(j+1));'];eval(str);str2=['fems=[fems;fem',num2str(j),'];'];eval(str2);endboundary1=inputBoundaryData('d','min',0);boundary2=inputBoundaryData('n','max',1j*k0*cos(theta(i)),2j*k0*cos(theta(i))*E0*exp(1j*k0*L*cos(theta(i))));[a,b,c]=createMatrixElements(fems);%依据FEM节点生成求解矩阵[K,b]=createMatrixK([boundary1,boundary2],a,b,c);%强加边界条件results=solveWithGuassianMethod(K,b);%高斯消元法求解R=(results(element_num+1)-E0*exp(1j*k0*L*cos(theta(i))))/E0*exp(-1j*k0*L*cos(theta(i)));plotData=[plotData;[theta(i),R]];
end
plot(plotData(:,1)*180/pi,abs(plotData(:,2)))相关文章:

金属衬底介质片对平面波的反射-问题的解析求解和FEM求解
金属衬底介质片对平面波的反射-问题的解析求解和FEM求解 参考有限元从零单排系列4 代码参考了上面大佬文章提供的,但是部分计算系数错了,我改了下加了许多注释,便于大家理解。 书籍参考的电磁场有限元方法(金建铭),所用的公式都…...

2023 年 9 月青少年软编等考 C 语言四级真题解析
目录 T1. 酒鬼T2. 大盗T3. 核电站思路分析T4. 盒子与小球之二思路分析T1. 酒鬼 此题为 2021 年 3 月四级第一题原题,见 2021 年 3 月青少年软编等考 C 语言四级真题解析中的 T1。 T2. 大盗 此题为 2021 年 6 月四级第二题原题,见 2021 年 6 月青少年软编等考 C 语言四级真…...

C++的内存四区
文章目录 内存四区1.程序运行前1.1 代码区2.1 全局区2.2 示例 2.程序运行后1.1 栈区1.2 堆区 内存四区 1.程序运行前 在程序编译后,生成了exe可执行程序,未执行该程序前分为两个区域。该区域的数据在程序结束后由操作系统释放. 1.1 代码区 存放 CPU …...

Java爬虫技术:按关键字搜索VIP商品详情
在数字化时代,电子商务平台的竞争日益激烈,而精准的数据采集和分析成为了企业获取竞争优势的关键。对于电商平台而言,能够根据用户输入的关键字快速搜索并展示VIP商品的详细信息,不仅能够提升用户体验,还能够增加销售机…...

C++ —— 模板类与函数
C —— 模板类与函数 模板类可以用于函数的参数和返回值,有三种形式: 普通函数,参数和返回值是模板类的实例化版本。函数模板,参数和返回值是某种的模板类。函数模板,参数和返回值是任意类型(支持普通类和…...

【软考高级】系统架构设计师复习笔记-精华版
文章目录 前言0 系统架构设计师0.1 考架构还是考系分0.2 架构核心知识0.3 架构教材变化 1 计算机操作系统1.1 cpu 组成1.2 内核的五大功能1.3 流水线技术1.4 段页式存储1.5 I/O 软件1.6 文件管理1.7 系统工程相关 2 嵌入式2.1 嵌入式技术2.2 板级支持包(BSP…...

免费 IP 归属地接口
免费GEOIP,查询IP信息,支持IPV4 IPV6 ,包含国家地理位置,维度,asm,邮编 等,例如 例如查询1.1.1.1 http://geoip.91hu.top/?ip1.1.1.1 返回json 对象...

AIA - IMSIC之二(附IMSIC处理流程图)
本文属于《 RISC-V指令集基础系列教程》之一,欢迎查看其它文章。 1 通过IMSIC接收外部中断的CSR 软件通过《AIA - 新增的CSR》描述的CSR来访问IMSIC。 machine level 的 CSR 与 IMSIC 的 machine level interrupt file 可相互互动;而 supervisor level 的 CSR…...

数据处理之数据规约
数据处理之数据规约 1. 数据规约概述 数据规约是数据处理中的重要方法,旨在让数据处理更简便、高效,以满足业务需求。当从数据仓库获取的数据量庞大时,直接在海量数据上进行分析和挖掘成本颇高。数据规约可得到数据集的归约表示,…...

爬虫代理服务要怎么挑选?
在数据采集的世界里,爬虫代理服务不仅帮助我们高效地收集信息,还能在保护数据安全方面发挥重要作用。但面对市场上琳琅满目的代理服务,我们该如何挑选呢?本文将为你提供一些实用的建议,帮助你找到最适合你的爬虫代理服…...
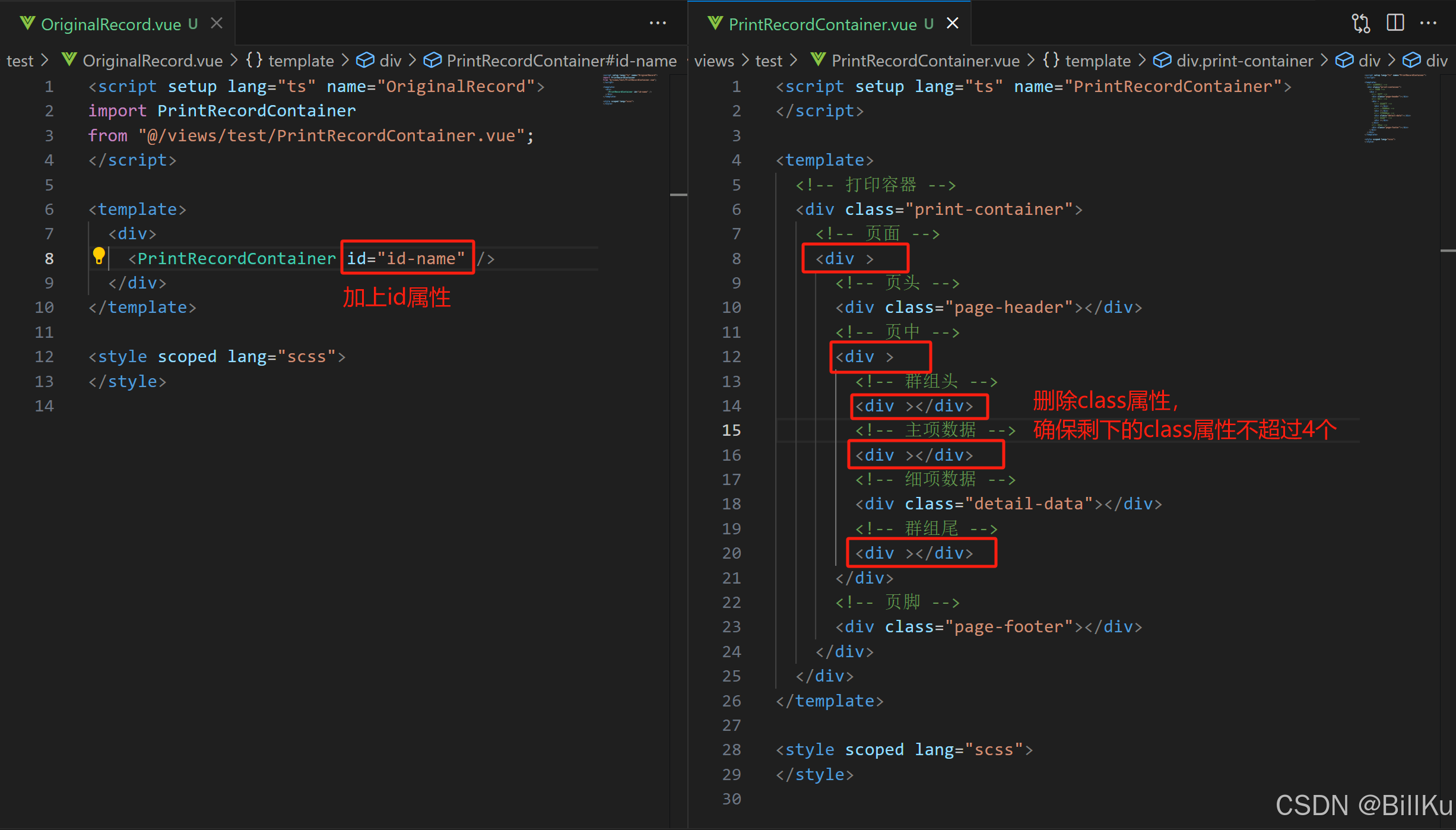
vue3组件调用解决奇怪问题的详细记录
左边是父组件,右边是子组件,运行正常: 父组件中的子组件加上class属性,运行报错:Extraneous non-props attributes (class) were passed to component but could not be automatically inherited because component re…...

【物联网技术与应用】实验16:模拟霍尔传感器实验
实验16 模拟霍尔传感器实验 【实验介绍】 基于霍尔效应,霍尔传感器是响应于磁场而改变其输出电压的传感器。霍尔传感器用于接近开关,定位,速度检测和电流检测应用。 霍尔传感器可以分为模拟霍尔传感器和开关霍尔传感器由电压调节器&#x…...

【机器学习案列】车牌自动识别系统:基于YOLO11的高效实现
🧑 博主简介:曾任某智慧城市类企业算法总监,目前在美国市场的物流公司从事高级算法工程师一职,深耕人工智能领域,精通python数据挖掘、可视化、机器学习等,发表过AI相关的专利并多次在AI类比赛中获奖。CSDN…...

高精度问题
目录 算法实现基础 高精度加法AB 测试链接 源代码 代码重点 高精度减法A-B 测试链接 源代码 代码重点 高精度乘法A*b和A*B 测试链接 源代码 代码重点 高精度除法A/b和A/B 测试链接 源代码 代码重点 高精度求和差积商余 算法实现基础 本算法调用STL…...

kong网关使用pre-function插件,改写接口的返回数据
一、背景 kong作为api网关,除了反向代理后端服务外,还可对接口进行预处理。 比如本文提及的一个小功能,根据http header某个字段的值,等于多少的时候,返回一个固定的报文。 使用到的kong插件是pre-function。 除了上…...

【QT开发自制小工具】PDF/图片转excel---调用百度OCR API接口
前言 前几年WPS还可以免费处理5页以内的PDF转excel,现在必须付费了,而且百度其他在线的PDF转excel都是要收费的,刚好前几年调研过百度OCR的高精度含位置接口,依然是每天可以免费调用50次,本篇是基于此接口,…...

vue2 elementui if导致的rules判断失效
优化目标 和 目标转化出价必填的 切换的时候还会隐藏掉 这时候的if语句会导致rules判断失效 我的办法是把判断拉到外面 别放在el-form-item里 <section v-if"unitForm.baseTarget OCPM && unitForm.cpaTargetOptions ! undefined && unitForm.cpaTa…...

DevOps实战:用Kubernetes和Argo打造自动化CI/CD流程(2)
DevOps实战:用Kubernetes和Argo打造自动化CI/CD流程(2) 背景 架构图 正片开始之前,请一定先熟悉上面的架构图,跟着我的步骤,一步一步执行成功,相信后续根据自己特定的需求定制CI/CD。 需求 …...

嵌入式科普(25)Home Assistant米家集成意味着IOT的核心是智能设备
目录 一、概述 二、一张图说尽HA 三、HA的相关资料 四、米家集成划重点 五、总结 一、概述 小米Home Assistant 米家集成开源一周star近15k,迭代4个版本,12个贡献者 本文科普一下Home Assistant(简称HA)、米家集成ÿ…...

spring cloud gateway 3
**Spring Cloud Gateway 3** 是 Spring Cloud 生态系统中的一个重要组件,用于构建 API 网关,提供路由、监控、安全等关键功能。以下是关于 Spring Cloud Gateway 3 的详细介绍: ## 1. 什么是 Spring Cloud Gateway? **Spring Clou…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
