dfs(八)数字的全排列 (含有重复项与非重复项)
如果每个数字任意取的话。就不需要加book标志位
没有重复项数字的全排列_牛客题霸_牛客网
描述
给出一组数字,返回该组数字的所有排列
例如:
[1,2,3]的所有排列如下
[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2], [3,2,1].
(以数字在数组中的位置靠前为优先级,按字典序排列输出。)数据范围:数字个数 0<n≤60<n≤6
要求:空间复杂度 O(n!)O(n!) ,时间复杂度 O(n!)O(n!)
示例1
输入:[1,2,3]返回值:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
普通的dfs模板套用加上一个book标志位,表示每一位元素是否被用过
class Solution {
public:vector<vector<int>> res;vector<int> temp;void dfs(vector<int> &num, int index, vector<bool>& book){if(index == num.size()){res.push_back(temp);return;}for(int i = 0; i < num.size(); i++){if(book[i]==false){book[i] = true; // 感觉像最近写的互斥锁哈哈哈哈temp.push_back(num[i]);dfs(num, index+1, book);temp.pop_back();book[i] = false;}}}vector<vector<int> > permute(vector<int> &num) {vector<bool> book (num.size(), false); // 设置一个book标志位,标志每一个数是否被用过dfs(num, 0, book);return res;}
};有重复项数字的全排列_牛客题霸_牛客网
描述
给出一组可能包含重复项的数字,返回该组数字的所有排列。结果以字典序升序排列。
数据范围: 0<n≤80<n≤8 ,数组中的值满足 −1≤val≤5−1≤val≤5
要求:空间复杂度 O(n!)O(n!),时间复杂度 O(n!)O(n!)
示例1
输入:[1,1,2]返回值:[[1,1,2],[1,2,1],[2,1,1]]
示例2
输入:[0,1]返回值:[[0,1],[1,0]]
class Solution {
public:vector<vector<int>> res;set<vector<int>> ress; // 使用set来接收vector<int> temp;void dfs(vector<int> &num, vector<bool> &book, int index){if(index == num.size()){ress.insert(temp);return;}for(int i = 0; i < num.size(); i++){if(book[i]){book[i] = false;temp.push_back(num[i]);dfs(num, book, index+1);temp.pop_back();book[i] = true;}}}vector<vector<int> > permuteUnique(vector<int> &num) {vector<bool> book (num.size(), true);dfs(num, book, 0);for(auto &e : ress) // 最终将set转化为vector{res.push_back(e);}return res;}
};
知识点:递归与回溯
递归是一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。因此递归过程,最重要的就是查看能不能讲原本的问题分解为更小的子问题,这是使用递归的关键。
如果是线型递归,子问题直接回到父问题不需要回溯,但是如果是树型递归,父问题有很多分支,我需要从子问题回到父问题,进入另一个子问题。因此回溯是指在递归过程中,从某一分支的子问题回到父问题进入父问题的另一子问题分支,因为有时候进入第一个子问题的时候修改过一些变量,因此回溯的时候会要求改回父问题时的样子才能进入第二子问题分支。
思路:
这道题类似没有重复项数字的全排列,但是因为交换位置可能会出现相同数字交换的情况,出现的结果需要去重,因此不便于使用交换位置的方法。
我们就使用临时数组去组装一个排列的情况:每当我们选取一个数组元素以后,就确定了其位置,相当于对数组中剩下的元素进行全排列添加在该元素后面,给剩余部分进行全排列就是一个子问题,因此可以使用递归。
- 终止条件: 临时数组中选取了n个元素,已经形成了一种排列情况了,可以将其加入输出数组中。
- 返回值: 每一层给上一层返回的就是本层级在临时数组中添加的元素,递归到末尾的时候就能添加全部元素。
- 本级任务: 每一级都需要选择一个不重复元素加入到临时数组末尾(遍历数组选择)。
回溯的思想也与没有重复项数字的全排列类似,对于数组[1,2,2,3],如果事先在临时数组中加入了1,后续子问题只能是[2,2,3]的全排列接在1后面,对于2开头的分支达不到,因此也需要回溯:将临时数组刚刚加入的数字pop掉,同时vis修改为没有加入,这样才能正常进入别的分支。
| 1 2 3 4 5 6 7 8 |
|
相关文章:

dfs(八)数字的全排列 (含有重复项与非重复项)
如果每个数字任意取的话。就不需要加book标志位 没有重复项数字的全排列_牛客题霸_牛客网 描述 给出一组数字,返回该组数字的所有排列 例如: [1,2,3]的所有排列如下 [1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2], [3,2,1]. (以数字在数组中的位…...

基于微信小程序的医院挂号系统小程序
文末联系获取源码 开发语言:Java 框架:ssm JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏览器…...

工程经验:残差连接对网络训练的巨大影响
文章目录1、没有使用残差连接的网络难以训练2、loss 不下降的原因3、使用了残差连接的网络可以高效训练1、没有使用残差连接的网络难以训练 经典的 SegNet 网络结构如下: 在使用上图所示的 SegNet 作为噪声预测网络训练扩散模型(DDPM)时&…...

靓号管理-搜索
搜索手机号: 最后一条就是使用的关键mobile__contains 使用字典: 后端的逻辑: """靓号列表"""data_dict {}search_data request.GET.get(q, "")# 根据关键字进行搜索,如果关键字存在&…...
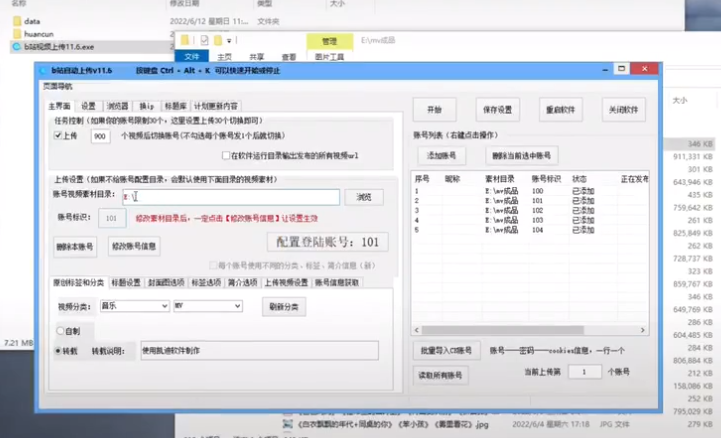
B站发帖软件哪个好用?好用的哔哩哔哩发帖工具
B站发帖软件哪个好用?好用的哔哩哔哩发帖工具#发帖软件#哔哩哔哩发帖#视频发布软件 登录成功之后,进入到这样一个界面,默认情况下是这个样子的,我们在这里输入一下我们的一个文件夹的路径,输入到这里,点击添加账号&a…...

docker
docker ps docker images 拉取ubuntu镜像 docker pull ubuntu 启动 docker start podid 进入bash界面 docker exec -it podid /bin/bash 安装sudo apt-get install sudo 更新使配置生效 sudo apt update 安装vim apt-get install vim 安装中文包 sudo apt-get i…...
Django by Example·第三章|Extending Your Blog Application@笔记
Django by Example第三章|Extending Your Blog Application笔记 之前已经写过两章内容了,继续第三章。第三章继续对博客系统的功能进行拓展,其中将会穿插一些重要的技术要点。 部分内容引用自原书,如果大家对这本书感兴趣 请支持原版Django …...

23.2.13 Drive development 设备树信息解析相关代码
1.练习课上代码 2.把设备树信息解析相关函数按照自己的理解发布CSDN 3.复习中断相关内核 IO多路复用---epoll 核心内容:一棵树一个链表三个方法 epoll会将要监听的事件文件描述符添加到内核里一颗红黑树上,当有事件发生,epoll会调用回调函数…...

智能工厂以MES系统为基础,实现"信息化减人,自动化换人"
MES是一种生产信息化的管理系统,它适用于制造业的车间实施层面。MES能够为企业提供生产数据、项目看板、库存、成本、工装、生产计划、计划排程、质量、人力资源、采购、生产过程控制、底层数据集成分析、上层数据集成分解等管理模块,为企业打造一个扎实…...

【数据挖掘实战】——电力窃漏电用户自动识别
【数据挖掘实战】——电力窃漏电用户自动识别一、背景和挖掘目标二、分析方法与过程1、初步分析2、数据抽取3、探索分析4、数据预处理5、构建专家样本三、构建模型1、构建窃漏电用户识别模型2、模型评价3、进行窃漏电诊断拓展思考项目代码地址:https://gitee.com/li…...
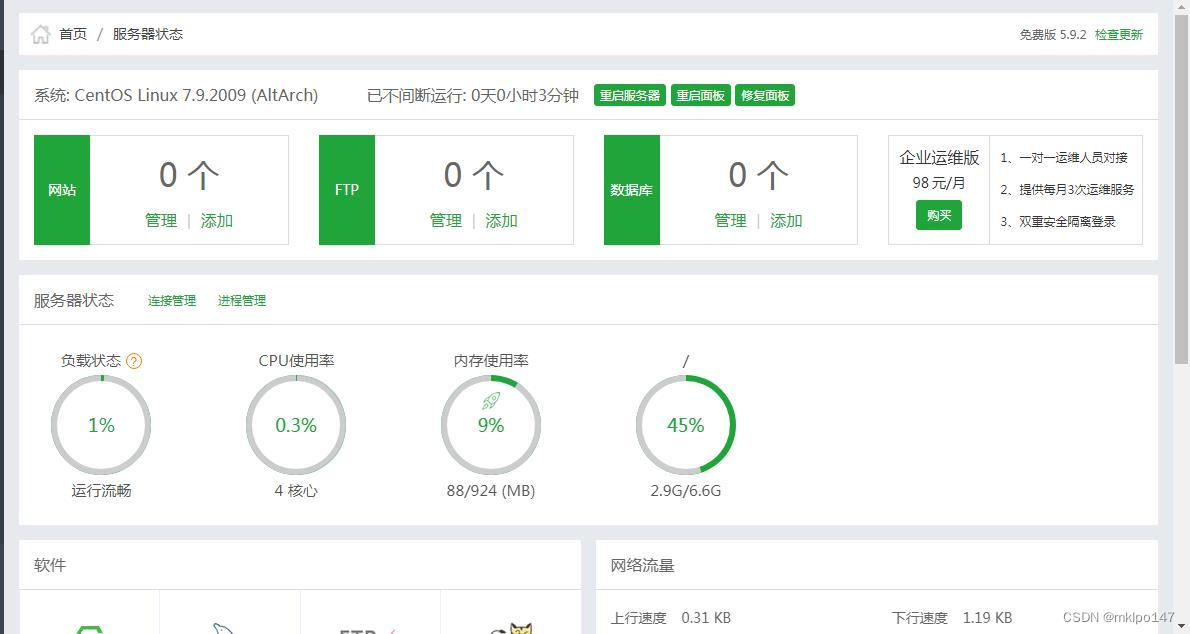
树莓派 安装 宝塔linux面板5.9. 2023-2-13
一.环境 1.硬件环境: 树莓派3b , 8GB tf卡 ,micro usb电源 2.网络环境: 网线直连路由器 , 可访问互联网 3.软件环境: 树莓派操作系统 CentOS-Userland-7-armv7hl-RaspberryPI-Minimal-2009-sda(linux) 系统刻录工具 Win32DiskImager (win) ip扫描工具 Adv…...

如何提高短视频的播放量-4个技巧
做短视频自媒体,点击率是第一位,点击量越多,粉丝也就越多。可是,怎么才能增加短视频的点击率和提高播放量呢?今天就来教大家4个技巧: 1、蹭热点 热门话题自带流量,它的热度和价值,是…...
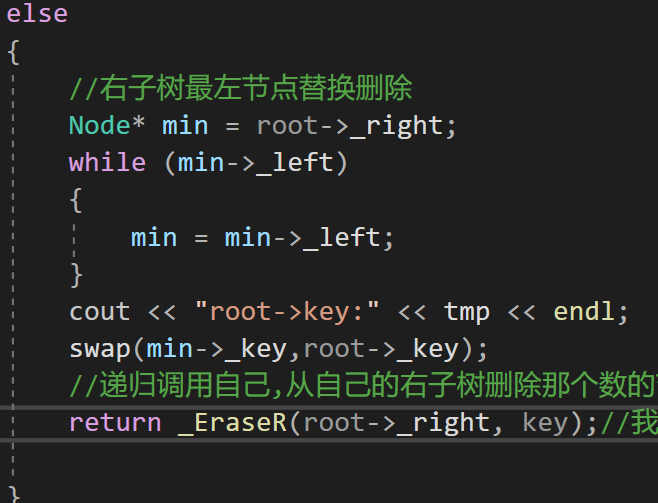
搜索二叉树
文章目录二叉搜索树模拟实现InsertInsertR()EraseEraseR搜索树的价值实现代码二叉搜索树 在二叉树的基础之上, 左子树的值都比根节点小,右子树都更大。那么他的左右子树也分别叫做二叉搜索树。 查找一个节点,最多查找高度次(建立在这个树是比较均衡的).10亿里面找…...

CentOS8基础篇5:用户账号与用户组的创建
一、用户与用户组概念 Linux是一个多用户、多任务的服务器操作系统,多用户多任务指可以在系统上建立多个用户,而多个用户可以在同一时间内登录同一个系统执行各自不同的任务,而互不影响。 Linux用户是根据角色定义的,具体分为三…...

阿里云服务器使用
服务器配置CPU&内存:2核(vCPU)2 GiB操作系统:Ubuntu 22.04 64位运行环境部署因为部署用到了nodejs首先,打开终端,并输入以下命令以安装必要的软件包:sudo apt-get install curl接着,使用 curl 命令安装…...

全国空气质量排行,云贵川和西藏新疆等地空气质量更好
哈喽,大家好,春节刚刚过去,不知道大家是不是都开始进入工作状态了呢?春节期间,允许燃放烟花爆竹的地区的朋友们不知道都去欣赏烟花表演没有?其他地区的朋友们相比烟花表演可能更关心燃放烟花爆竹造成的环境…...

Learning C++ No.8【内存管理】
引言: 北京时间:2023/2/12/18:04,昨天下午到达学校,摆烂到现在,该睡睡,该吃吃,该玩玩,在一顿操作之下,目前作息调整好了一些,在此记录,2月11&…...

『 MySQL篇 』:MySQL表的相关约束
基础篇 MySQL系列专栏(持续更新中 …)1『 MySQL篇 』:库操作、数据类型2『 MySQL篇 』:MySQL表的CURD操作3『 MySQL篇 』:MySQL表的相关约束文章目录 1 . 非空约束 (not null)2 . 唯一性约束(unique)3 . check约束4 . 默认约束(default)5 . 主…...

家政服务小程序实战教程10-分类展示
小程序一般底部菜单栏会有一个分类的功能,点击分类,以侧边栏导航的形式列出所有类目,点击某个类目可以做数据筛选,我们本篇就实现一下该功能 01 优化数据源 在我们家政服务小程序里,我们已经建立了类型和服务的数据源…...

一篇文章带你学会Ansible的安装及部署
目录 前言 一、什么是Ansible 二、Ansible的工作方式 三、Ansible的安装 四、构建Anisble清单 1、清单书写方式 2、清单查看 3、清单书写规则 4、主机规格的范围化操作 五、ansible命令指定清单的正则表达式 六、 Ansible配置文件参数详解 1、配置文件的分类与优先…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
