基于pytorch的深度学习基础3——模型创建与nn.Module

三 模型创建与nn.Module

3.1 nn.Module

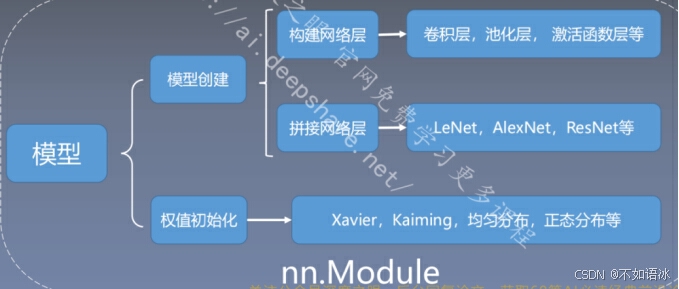
模型构建两要素：

1. 构建子模块——__init()__
2. 拼接子模块——forward（）

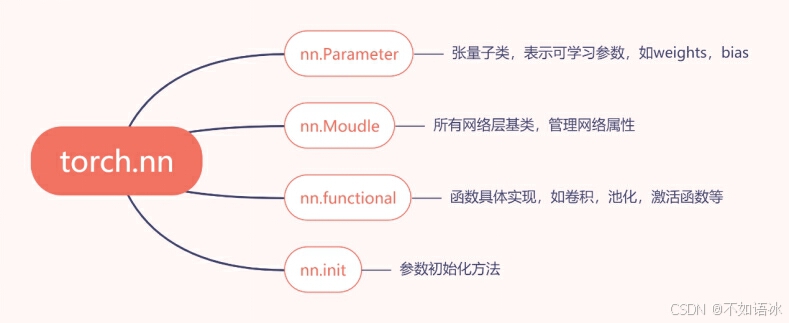
一个module可以有多个module；

一个module相当于一个运算，都必须实现forward函数；

每一个module有8个字典管理属性。

self._parameters = OrderedDict()

self._buffers = OrderedDict()

self._backward_hooks = OrderedDict()

self._forward_hooks = OrderedDict()

self._forward_pre_hooks = OrderedDict()

self._state_dict_hooks = OrderedDict()

self._load_state_dict_pre_hooks = OrderedDict()

self._modules = OrderedDict()

3.2 网络容器

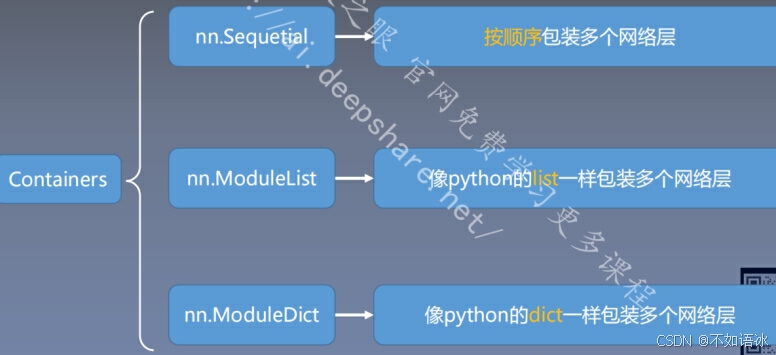
nn.Sequential()

是nn.Module()的一个容器，用于按照顺序包装一组网络层；

顺序性：网络层之间严格按照顺序构建；

自带forward（）：

各网络层之间严格按顺序执行，常用于block构建

class LeNetSequential(nn.Module):

    def __init__(self, classes):

        super(LeNetSequential, self).__init__()

        self.features = nn.Sequential(

            nn.Conv2d(3, 6, 5),

            nn.ReLU(),

            nn.MaxPool2d(kernel_size=2, stride=2),

            nn.Conv2d(6, 16, 5),

            nn.ReLU(),

            nn.MaxPool2d(kernel_size=2, stride=2),)

        self.classifier = nn.Sequential(

            nn.Linear(16*5*5, 120),

            nn.ReLU(),

            nn.Linear(120, 84),

            nn.ReLU(),

            nn.Linear(84, classes),)

    def forward(self, x):

        x = self.features(x)

        x = x.view(x.size()[0], -1)

        x = self.classifier(x)

        return x

nn.ModuleList()

是nn.Module的容器，用于包装网络层，以迭代方式调用网络层。

主要方法：

append()：在ModuleList后面添加网络层；

extend（）:拼接两个ModuleList.

Insert():指定在ModuleList中插入网络层。

nn.ModuleList：迭代性，常用于大量重复网构建，通过for循环实现重复构建

class ModuleList(nn.Module):

    def __init__(self):

        super(ModuleList, self).__init__()

        self.linears = nn.ModuleList([nn.Linear(10, 10) for i in range(20)])

    def forward(self, x):

        for i, linear in enumerate(self.linears):

            x = linear(x)

        return x

nn.ModuleDict()

以索引方式调用网络层

主要方法：

• clear()：清空ModuleDict

• items()：返回可迭代的键值对(key-value pairs)

• keys()：返回字典的键(key)

• values()：返回字典的值(value)

• pop()：返回一对键值，并从字典中删除

n.ModuleDict：索引性，常用于可选择的网络层

class ModuleDict(nn.Module):

    def __init__(self):

        super(ModuleDict, self).__init__()

        self.choices = nn.ModuleDict({

            'conv': nn.Conv2d(10, 10, 3),

            'pool': nn.MaxPool2d(3)

        })

        self.activations = nn.ModuleDict({

            'relu': nn.ReLU(),

            'prelu': nn.PReLU()

        })

    def forward(self, x, choice, act):

        x = self.choices[choice](x)

        x = self.activations[act](x)

        return x

3.3卷积层

nn.ConV2d()

nn.Conv2d(in_channels, out_channels,kernel_size, stride=1,padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')

in_channels：输入通道数，比如RGB图像是3，而后续的网络层的输入通道数为前一卷积层的输出通道数；

out_channels：输出通道数，等价于卷积核个数

kernel_size：卷积核尺寸

stride：步

padding：填充个数

dilation：空洞卷积大小

groups：分组卷积设置

bias：偏置

    conv_layer = nn.Conv2d(3, 1, 3)   # input:(i, o, size) weights:(o, i , h, w)

    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation

    img_conv = conv_layer(img_tensor)

这里使用 input*channel 为 3，output_channel 为 1 ，卷积核大小为 3×3 的卷积核nn.Conv2d(3, 1, 3)，使用nn.init.xavier_normal*()方法初始化网络的权值。

我们通过`conv_layer.weight.shape`查看卷积核的 shape 是`(1, 3, 3, 3)`，对应是`(output_channel, input_channel, kernel_size, kernel_size)`。所以第一个维度对应的是卷积核的个数，每个卷积核都是`(3,3,3)`。虽然每个卷积核都是 3 维的，执行的却是 2 维卷积。

转置卷积nn.ConvTranspose2d

转置卷积又称为反卷积(Deconvolution)和部分跨越卷积(Fractionally-stridedConvolution) ，用于对图像进行上采样(UpSample)

为什么称为转置卷积？

假设图像尺寸为4*4，卷积核为3*3，padding=0，stride=1

正常卷积：

转置卷积：

假设图像尺寸为2*2，卷积核为3*3，padding=0，stride=1

nn.ConvTranspose2d(in_channels, out_channels,

kernel_size,

stride=1,

padding=0,

output_padding=0,

groups=1,

bias=True,

dilation=1, padding_mode='zeros')

输出尺寸计算：

# flag = 1

flag = 0

if flag:

    conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2)   # input:(i, o, size)

    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation

    img_conv = conv_layer(img_tensor)

print("卷积前尺寸:{}\n卷积后尺寸:{}".format(img_tensor.shape, img_conv.shape))

img_conv = transform_invert(img_conv[0, 0:1, ...], img_transform)

img_raw = transform_invert(img_tensor.squeeze(), img_transform)

plt.subplot(122).imshow(img_conv, cmap='gray')

plt.subplot(121).imshow(img_raw)

plt.show()

3.4池化层nn.MaxPool2d && nn.AvgPool2d

池化运算：对信号进行 “收集”并 “总结”，类似水池收集水资源，因而

得名池化层

“收集”：多变少

“总结”：最大值/平均值

nn.MaxPool2d

nn.MaxPool2d(kernel_size, stride=None,

padding=0, dilation=1,

return_indices=False,

ceil_mode=False)

主要参数：

• kernel_size：池化核尺寸

• stride：步长

• padding ：填充个数

• dilation：池化核间隔大小

• ceil_mode：尺寸向上取整

• return_indices：记录池化像素索引

# flag = 1

flag = 0

if flag:

    maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2))   # input:(i, o, size) weights:(o, i , h, w)

    img_pool = maxpool_layer(img_tensor)

nn.AvgPool2d

nn.AvgPool2d(kernel_size,

stride=None,

padding=0,

ceil_mode=False,

count_include_pad=True,

divisor_override=None)

主要参数：

• kernel_size：池化核尺寸

• stride：步长

• padding ：填充个数

• ceil_mode：尺寸向上取整

• count_include_pad：填充值用于计算

• divisor_override ：除法因子

    avgpoollayer = nn.AvgPool2d((2, 2), stride=(2, 2))   # input:(i, o, size) weights:(o, i , h, w)

    img_pool = avgpoollayer(img_tensor)

    img_tensor = torch.ones((1, 1, 4, 4))

    avgpool_layer = nn.AvgPool2d((2, 2), stride=(2, 2), divisor_override=3)

    img_pool = avgpool_layer(img_tensor)

    print("raw_img:\n{}\npooling_img:\n{}".format(img_tensor, img_pool))

nn.MaxUnpool2d

功能：对二维信号（图像）进行最大值池化

上采样

主要参数：

• kernel_size：池化核尺寸

• stride：步长

• padding ：填充个数

    # pooling

    img_tensor = torch.randint(high=5, size=(1, 1, 4, 4), dtype=torch.float)

    maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2), return_indices=True)

    img_pool, indices = maxpool_layer(img_tensor)

    # unpooling

    img_reconstruct = torch.randn_like(img_pool, dtype=torch.float)

    maxunpool_layer = nn.MaxUnpool2d((2, 2), stride=(2, 2))

    img_unpool = maxunpool_layer(img_reconstruct, indices)

    print("raw_img:\n{}\nimg_pool:\n{}".format(img_tensor, img_pool))

    print("img_reconstruct:\n{}\nimg_unpool:\n{}".format(img_reconstruct, img_unpool))

3.5线性层

nn.Linear(in_features, out_features, bias=True)

功能：对一维信号（向量）进行线性组合

主要参数：

• in_features：输入结点数

• out_features：输出结点数

• bias ：是否需要偏置

计算公式：y = 𝒙𝑾𝑻 + 𝒃𝒊𝒂s

    inputs = torch.tensor([[1., 2, 3]])

    linear_layer = nn.Linear(3, 4)

    linear_layer.weight.data = torch.tensor([[1., 1., 1.],

                                             [2., 2., 2.],

                                             [3., 3., 3.],

                                             [4., 4., 4.]])

    linear_layer.bias.data.fill_(0.5)

    output = linear_layer(inputs)

    print(inputs, inputs.shape)

    print(linear_layer.weight.data, linear_layer.weight.data.shape)

    print(output, output.shape)

3.6 激活函数层

nn.Sigmoid

nn.tanh:

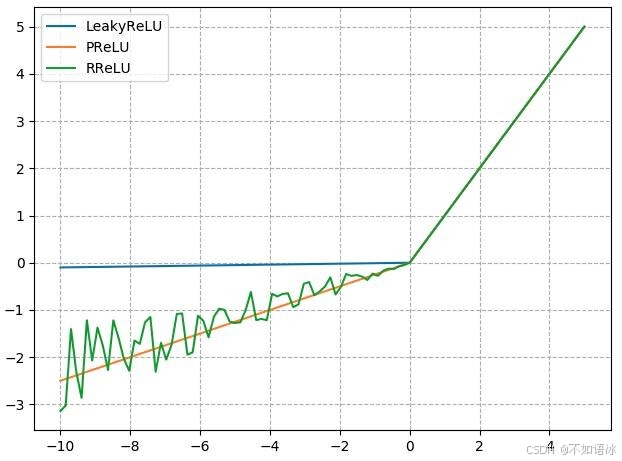
nn.ReLU

nn.LeakyReLU

negative_slope: 负半轴斜率

nn.PReLU

init: 可学习斜率

nn.RReLU

lower: 均匀分布下限

upper:均匀分布上限

参考资料

深度之眼课程