深入理解 PyTorch 的 view() 函数:以多头注意力机制(Multi-Head Attention)为例 (中英双语)
深入理解 PyTorch 的 view() 函数:以多头注意力机制(Multi-Head Attention)为例
在深度学习模型的实现中,view() 是 PyTorch 中一个非常常用的张量操作函数,它能够改变张量的形状(shape)而不改变数据的内容。本文将结合多头注意力机制中的具体实现,详细解析 view() 的作用、使用场景及其与其他操作的结合。
一、view() 函数的基本概念
view() 是 PyTorch 提供的一个高效重塑张量形状的函数。其功能类似于 NumPy 的 reshape(),但它要求张量的内存布局是连续的。如果张量不连续,需要先使用 .contiguous() 方法让张量变成连续的内存布局。
语法:
tensor.view(*shape)
tensor:需要被重新调整形状的张量。*shape:目标形状,-1表示自动推导维度大小,确保数据总量不变。
使用注意事项:
- 数据总量(元素数量)必须保持不变:
- 如果原始张量的形状为
(a, b),则新形状中各维度的乘积必须等于a * b。
- 如果原始张量的形状为
- 连续性要求:
- 如果张量在内存中不是连续存储的,调用
view()会报错,需要先调用.contiguous()。
- 如果张量在内存中不是连续存储的,调用
二、结合多头注意力机制理解 view() 的作用
在多头注意力机制(Multi-Head Attention, MHA)中,需要将输入的张量沿最后一维切分成多个“头”(head)。我们以以下代码为例,逐步分析 view() 的实际作用。
q, k, v = self.q_proj(x), self.k_proj(x), self.v_proj(x)
假设输入张量:
x 的形状为 (B, T, C):
B:Batch size,表示每个 batch 的样本数。T:序列长度。C:特征维度(通道数)。
多头注意力需要将最后一维 C 切分成 n_head 个头,每个头的维度是 head_size = C // n_head,从而得到形状为 (B, T, n_head, head_size) 的张量。以下是具体的代码实现和解读。
三、代码实现与解析
1. 重新调整张量形状:切分多头
k = k.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
q = q.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
v = v.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
-
view(B, T, self.n_head, C // self.n_head):- 使用
view()将原始张量(B, T, C)调整为(B, T, n_head, head_size),其中head_size = C // n_head。 - 每个维度的具体含义:
B:Batch size。T:序列长度。n_head:多头数量。head_size:每个头的特征维度。
- 目的:切分出多头,每个头独立计算注意力。
- 使用
-
.transpose(1, 2):- 调整维度顺序,将形状从
(B, T, n_head, head_size)转换为(B, n_head, T, head_size)。 - 目的:为了后续计算注意力时,每个头可以独立计算。
- 调整维度顺序,将形状从
2. 计算注意力权重
att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1))) # (B, nh, T, T)
att = F.softmax(att, dim=-1)
q @ k.transpose(-2, -1):- 计算查询向量(query)与键向量(key)的点积。
k.transpose(-2, -1)将k的最后两维转置,从(B, nh, T, hs)转换为(B, nh, hs, T),以便进行矩阵乘法。- 最终
att的形状为(B, nh, T, T),表示每个头的注意力得分矩阵。
3. 添加 Mask
详细解释请看文末。
att = att.masked_fill(self.bias[:,:,:T,:T] == 0, torch.finfo(x.dtype).min)
- 通过 Mask 确保每个位置只关注前面的序列。
4. 计算加权输出并恢复形状
y = att @ v # (B, nh, T, hs)
y = y.transpose(1, 2).contiguous().view(B, T, C)
y = self.o_proj(y)
-
att @ v:- 使用注意力得分加权值向量
v,输出形状为(B, nh, T, hs)。
- 使用注意力得分加权值向量
-
y.transpose(1, 2):- 调整维度顺序,将形状从
(B, nh, T, hs)转换为(B, T, nh, hs)。
- 调整维度顺序,将形状从
-
.view(B, T, C):- 使用
view()将多头的输出重新组合为单个张量,恢复到原始特征维度。
- 使用
四、总结:view() 的核心作用
-
切分特征维度:
view()将张量沿最后一维切分成多头,为每个头的独立计算创造条件。
-
调整张量形状:
- 将
(B, T, C)重塑为(B, T, n_head, head_size),然后通过transpose()等操作方便后续矩阵运算。
- 将
-
恢复原始形状:
- 最终通过
view()将多头输出重新组合成单个张量,便于后续网络层处理。
- 最终通过
view() 的使用贯穿整个多头注意力机制的实现,其灵活性和高效性使其成为 PyTorch 中不可或缺的操作函数。
五、view() 与其他操作的对比
reshape():更通用,不要求张量是连续的,但可能会引入额外开销。.contiguous():与view()配合使用,确保张量的内存布局连续。
六、完整代码示例
以下是一个完整的代码示例,展示如何通过 view() 实现多头注意力机制:
import torch
import torch.nn.functional as F
import math# 假设输入数据
B, T, C = 4, 512, 128
n_head = 8
head_size = C // n_head
x = torch.randn(B, T, C)# 线性变换
q_proj = torch.nn.Linear(C, C)
k_proj = torch.nn.Linear(C, C)
v_proj = torch.nn.Linear(C, C)
o_proj = torch.nn.Linear(C, C)# 计算 Q, K, V
q = q_proj(x)
k = k_proj(x)
v = v_proj(x)# 切分多头
q = q.view(B, T, n_head, head_size).transpose(1, 2) # (B, n_head, T, head_size)
k = k.view(B, T, n_head, head_size).transpose(1, 2) # (B, n_head, T, head_size)
v = v.view(B, T, n_head, head_size).transpose(1, 2) # (B, n_head, T, head_size)# 注意力机制
att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(head_size))
att = F.softmax(att, dim=-1)
y = att @ v # (B, n_head, T, head_size)# 恢复形状
y = y.transpose(1, 2).contiguous().view(B, T, C) # (B, T, C)
y = o_proj(y)
希望本文对理解 PyTorch 的 view() 函数以及其在多头注意力机制中的应用有所帮助.
英文版
Understanding PyTorch’s view() Function: An Example with Multi-Head Attention (MHA)
In PyTorch, the view() function is a powerful tool for reshaping tensors. It is frequently used in deep learning to manipulate tensor shapes for specific tasks, such as in the implementation of Multi-Head Attention (MHA). This blog post will break down the purpose, functionality, and application of view() in the context of MHA, using a concrete example.
1. What is view()?
The view() function in PyTorch is used to reshape a tensor without changing its data. It is analogous to NumPy’s reshape() function, but with a key requirement: the tensor must have a contiguous memory layout.
Syntax:
tensor.view(*shape)
tensor: The tensor to reshape.*shape: The new shape for the tensor. A-1can be used for one dimension to infer its size automatically, provided the total number of elements remains constant.
Key Points:
- The total number of elements must remain the same:
- For example, a tensor of shape
(4, 128)can be reshaped into(8, 64)but not into(5, 64)because4 * 128 != 5 * 64.
- For example, a tensor of shape
- The tensor must have contiguous memory:
- If the tensor isn’t contiguous, you must first call
.contiguous()before usingview().
- If the tensor isn’t contiguous, you must first call
2. Why Use view() in Multi-Head Attention?
Multi-Head Attention (MHA) splits the feature dimension of the input into multiple “heads.” Each head independently performs attention calculations, and the results are combined at the end. This requires reshaping tensors to group the feature dimension into multiple heads while preserving the other dimensions (like batch size and sequence length).
Input Shape:
Suppose the input tensor x has a shape of (B, T, C):
B: Batch size.T: Sequence length.C: Feature dimension.
If we want to use n_head heads in the attention mechanism, the feature dimension C is split into n_head groups, where each group has a size of head_size = C // n_head.
The tensor is reshaped to (B, T, n_head, head_size) for this purpose. To facilitate calculations, the dimensions are then transposed to (B, n_head, T, head_size).
3. Code Implementation: Reshaping for MHA
Here’s how the reshaping is implemented in MHA:
k = k.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, n_head, T, head_size)
q = q.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, n_head, T, head_size)
v = v.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, n_head, T, head_size)
Breaking it Down:
-
view(B, T, self.n_head, C // self.n_head):- Reshapes the tensor from
(B, T, C)to(B, T, n_head, head_size), where:Bis the batch size.Tis the sequence length.n_headis the number of attention heads.head_size = C // n_headis the size of each head.
- This effectively splits the feature dimension into
n_headseparate heads.
- Reshapes the tensor from
-
.transpose(1, 2):- Swaps the sequence length dimension (
T) with the head dimension (n_head), resulting in a shape of(B, n_head, T, head_size). - This format is required for the attention mechanism, as each head performs its operations independently on the sequence.
- Swaps the sequence length dimension (
4. Applying Attention and Masking
Once the input tensors (q, k, v) are reshaped, attention scores are computed, masked, and the output is calculated as follows:
Attention Computation:
att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1))) # (B, n_head, T, T)
att = F.softmax(att, dim=-1)
q @ k.transpose(-2, -1):- Computes the dot product of the query (
q) and the transposed key (k), resulting in a shape of(B, n_head, T, T). This represents the attention scores for each head. k.transpose(-2, -1)changeskfrom(B, n_head, T, head_size)to(B, n_head, head_size, T)to align dimensions for the dot product.
- Computes the dot product of the query (
Masking:
att = att.masked_fill(self.bias[:,:,:T,:T] == 0, torch.finfo(x.dtype).min)
- A mask is applied to ensure that positions cannot “see” future tokens in the sequence.
Output Calculation:
y = att @ v # (B, n_head, T, head_size)
y = y.transpose(1, 2).contiguous().view(B, T, C) # (B, T, C)
y = self.o_proj(y)
-
att @ v:- Multiplies the attention scores with the value (
v) tensor, resulting in a shape of(B, n_head, T, head_size).
- Multiplies the attention scores with the value (
-
transpose(1, 2):- Swaps the
n_headdimension withTto prepare for reshaping.
- Swaps the
-
.contiguous().view(B, T, C):- Flattens the heads back into a single feature dimension, restoring the original shape
(B, T, C).
- Flattens the heads back into a single feature dimension, restoring the original shape
5. The Role of view()
The view() function is crucial for:
-
Splitting Dimensions:
- It divides the feature dimension (
C) into multiple heads (n_head) for independent attention calculations.
- It divides the feature dimension (
-
Restoring Dimensions:
- After attention calculations, it combines the outputs of all heads back into a single feature dimension.
6. Example Code
Below is the complete example of reshaping for MHA:
import torch
import torch.nn.functional as F
import math# Example input
B, T, C = 4, 512, 128
n_head = 8
head_size = C // n_head
x = torch.randn(B, T, C)# Linear projections
q_proj = torch.nn.Linear(C, C)
k_proj = torch.nn.Linear(C, C)
v_proj = torch.nn.Linear(C, C)
o_proj = torch.nn.Linear(C, C)# Compute Q, K, V
q = q_proj(x)
k = k_proj(x)
v = v_proj(x)# Reshape for multi-head attention
q = q.view(B, T, n_head, head_size).transpose(1, 2) # (B, n_head, T, head_size)
k = k.view(B, T, n_head, head_size).transpose(1, 2) # (B, n_head, T, head_size)
v = v.view(B, T, n_head, head_size).transpose(1, 2) # (B, n_head, T, head_size)# Attention
att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(head_size))
att = F.softmax(att, dim=-1)
y = att @ v # (B, n_head, T, head_size)# Restore original shape
y = y.transpose(1, 2).contiguous().view(B, T, C) # (B, T, C)
y = o_proj(y)
7. Summary
The view() function plays a critical role in tensor manipulation for multi-head attention by enabling:
- Efficient splitting of dimensions into multiple heads.
- Seamless reshaping of tensor shapes for independent attention calculations.
- Reconstruction of the original shape after attention processing.
By combining view() with operations like transpose(), MHA becomes both efficient and modular, making it a cornerstone of modern NLP architectures.
【1】代码分析:att = att.masked_fill(self.bias[:,:,:T,:T] == 0, torch.finfo(x.dtype).min)
这行代码的目的是在 计算注意力分数(attention scores)后,对其进行遮掩(masking),以确保在某些情况下(如自回归模型的解码过程)当前位置无法访问未来的位置信息。
下面分步骤详细讲解这行代码的含义和作用:
1. self.bias[:,:,:T,:T]
含义:
self.bias是一个用于遮掩的矩阵,通常是一个 上三角矩阵(triangular matrix),大小为(1, 1, max_length, max_length)。- 它的作用是为注意力分数提供一种机制,来限制某些位置的访问。比如,在自回归任务中,每个时间步只允许看到当前及之前的时间步,不能看到未来的时间步。
max_length是模型支持的最大序列长度,T是当前序列的实际长度。通过self.bias[:,:,:T,:T]截取一个大小为(1, 1, T, T)的子矩阵,表示当前序列的遮掩规则。
举例:
假设 T = 4,截取后的子矩阵形状为 (1, 1, 4, 4),其内容可能如下:
self.bias[:,:,:T,:T] =
[[[[1, 0, 0, 0],[1, 1, 0, 0],[1, 1, 1, 0],[1, 1, 1, 1]]]]
- 1 表示允许访问,0 表示禁止访问。
- 这种矩阵通常由
torch.tril()函数生成(下三角部分为 1,上三角部分为 0)。
2. self.bias[:,:,:T,:T] == 0
含义:
== 0将遮掩矩阵中的 0 位置标记为True,表示这些位置需要被屏蔽。- 结果是一个布尔矩阵,形状仍然为
(1, 1, T, T)。
举例:
对应上面的例子:
self.bias[:,:,:T,:T] == 0 =
[[[[False, True, True, True],[False, False, True, True],[False, False, False, True],[False, False, False, False]]]]
3. torch.finfo(x.dtype).min
含义:
torch.finfo(x.dtype).min表示当前数据类型(x.dtype)的最小值。- 例如,如果
x的数据类型是float32,那么torch.finfo(torch.float32).min的值约为-3.4e38。 - 这个极小值被用作屏蔽位置的填充值,因为在后续的 Softmax 操作中,极小值的指数将接近于 0,从而使这些位置的注意力权重为 0。
4. att.masked_fill(...)
含义:
masked_fill(mask, value)是 PyTorch 中的一种操作,用于根据布尔掩码mask将张量中对应位置填充为指定的值value。- 在这段代码中,
att是注意力分数矩阵,形状为(B, n_head, T, T),其中:B是批量大小。n_head是注意力头的数量。T是序列长度。
- 通过
masked_fill()操作,将遮掩矩阵中为True的位置(即不允许访问的位置)填充为极小值torch.finfo(x.dtype).min。
5. 完整作用
这行代码的作用是:
- 将注意力分数矩阵
att中 不允许访问的位置 设置为极小值,以确保这些位置在 Softmax 计算时权重接近于 0,从而被忽略。
6. 举例说明
假设:
att的形状为(1, 1, 4, 4),内容如下:
att =
[[[[0.1, 0.2, 0.3, 0.4],[0.5, 0.6, 0.7, 0.8],[0.9, 1.0, 1.1, 1.2],[1.3, 1.4, 1.5, 1.6]]]]
- 对应的遮掩矩阵:
self.bias[:,:,:4,:4] == 0 =
[[[[False, True, True, True],[False, False, True, True],[False, False, False, True],[False, False, False, False]]]]
- 极小值(例如
-1e9)用于屏蔽。
执行 att = att.masked_fill(self.bias[:,:,:4,:4] == 0, -1e9) 后:
att =
[[[[ 0.1, -1e9, -1e9, -1e9],[ 0.5, 0.6, -1e9, -1e9],[ 0.9, 1.0, 1.1, -1e9],[ 1.3, 1.4, 1.5, 1.6]]]]
7. 总结
这行代码实现了遮掩逻辑,用于屏蔽注意力机制中不应该访问的位置,其主要作用如下:
- 限制注意力范围:确保当前时间步无法访问未来时间步的信息(例如语言模型的解码阶段)。
- 保留无效位置的注意力权重为 0:通过填充极小值,使这些位置在 Softmax 操作后被忽略。
这对于自回归任务(如 GPT 类模型)和其他需要时间步约束的任务至关重要。
【2】代码分析:q = q_proj(x) 是怎么做的?
q_proj(x) 是通过一个线性层(torch.nn.Linear)对输入张量 x 进行线性变换,最终输出一个和输入形状相同的张量(除非特意改变输出维度)。
1. 线性层的作用
torch.nn.Linear 是 PyTorch 中的全连接层(fully connected layer),它的作用是:
y = x ⋅ W T + b \text{y} = \text{x} \cdot \text{W}^T + \text{b} y=x⋅WT+b
- 输入矩阵:
x的形状为(B, T, C),其中:B是批量大小(batch size)。T是序列长度(sequence length)。C是特征维度(embedding size)。
- 权重矩阵:
W是线性层的权重,形状为(C, C)。 - 偏置向量:
b是线性层的偏置,形状为(C,)。 - 输出矩阵:结果
y的形状与输入x的形状一致,即(B, T, C)。
2. q_proj 的定义
q_proj 是一个线性层,初始化时:
q_proj = torch.nn.Linear(C, C)
- 该线性层将输入张量
x的最后一维(大小为C)映射到一个同样大小为C的新表示。 q_proj的内部参数:- 权重矩阵
W_q,形状为(C, C)。 - 偏置向量
b_q,形状为(C,)。
- 权重矩阵
3. q_proj(x) 的执行过程
当执行 q_proj(x) 时,会进行以下操作:
- 矩阵乘法:将输入张量
x的最后一维与权重矩阵W_q相乘。- 输入
x的形状为(B, T, C),与W_q的形状(C, C)相乘,最后一维变换为新表示。 - 输出结果为形状
(B, T, C)。
- 输入
- 加偏置:在矩阵乘法的结果上,加上偏置向量
b_q,偏置会广播到每个位置。
4. 举例说明
假设:
- 输入张量
x的形状为(4, 512, 128):
每个元素随机生成。x = torch.randn(4, 512, 128) - 权重矩阵
W_q的形状为(128, 128),偏置b_q的形状为(128,)。
执行 q_proj(x) 时:
- 矩阵乘法:每个时间步(
T=512)和批次(B=4)中的向量(大小为 128)都会与权重矩阵W_q(大小为 128×128)相乘,得到一个新的大小为 128 的向量。 - 加偏置:在每个位置上,加上偏置向量
b_q。
最终输出张量 q 的形状仍为 (4, 512, 128),但内容经过线性变换,表示的是对输入张量 x 的一种特征提取。
5. 小例子
假设:
-
输入
x为(B=2, T=3, C=4)的张量:x = torch.tensor([[[1.0, 2.0, 3.0, 4.0],[5.0, 6.0, 7.0, 8.0],[9.0, 10.0, 11.0, 12.0]],[[13.0, 14.0, 15.0, 16.0],[17.0, 18.0, 19.0, 20.0],[21.0, 22.0, 23.0, 24.0]]]) -
权重矩阵
W_q初始化为:W_q = torch.tensor([[1.0, 0.0, 0.0, 0.0],[0.0, 1.0, 0.0, 0.0],[0.0, 0.0, 1.0, 0.0],[0.0, 0.0, 0.0, 1.0]]) # 单位矩阵偏置向量
b_q为:b_q = torch.tensor([1.0, 1.0, 1.0, 1.0])
执行 q_proj(x):
- 矩阵乘法:
x的每个向量与W_q相乘(这里W_q是单位矩阵,所以输出等于输入)。
- 加偏置:
- 每个向量加上偏置
[1.0, 1.0, 1.0, 1.0]。
- 每个向量加上偏置
输出 q 为:
q = [[[ 2.0, 3.0, 4.0, 5.0],[ 6.0, 7.0, 8.0, 9.0],[10.0, 11.0, 12.0, 13.0]],[[14.0, 15.0, 16.0, 17.0],[18.0, 19.0, 20.0, 21.0],[22.0, 23.0, 24.0, 25.0]]]
6. 总结
q_proj(x)的作用是对输入x的最后一维(特征维度)进行线性变换,提取注意力机制中需要的查询特征(Query)。- 输入和输出形状保持一致,内容经过了权重矩阵和偏置的变换。
- 在多头注意力(Multi-Head Attention)中,这种线性变换用于生成 Query、Key 和 Value,以便进一步计算注意力分数和上下文表示。
【3】 q @ k.transpose(-2, -1) 是如何进行矩阵乘法的?
q @ k.transpose(-2, -1) 是在多头自注意力机制(Multi-Head Self-Attention)中计算查询向量(query)与键向量(key)的点积注意力分数(attention score)的关键步骤。
具体过程如下:
-
q的形状:查询向量q的形状为(B, nh, T, hs),其中:B是批量大小(batch size)。nh是注意力头的数量(number of heads)。T是序列长度(sequence length)。hs是单个注意力头的特征维度(head size)。
-
k.transpose(-2, -1)的形状:键向量k的形状原本为(B, nh, T, hs),通过k.transpose(-2, -1),将最后两维交换,变成(B, nh, hs, T)。 -
矩阵乘法:
q @ k.transpose(-2, -1)是两个张量的矩阵乘法:- 查询向量
q的最后两维(T, hs),与转置后的键向量k.transpose(-2, -1)的前两维(hs, T)相乘。 - 结果是一个新的张量,形状为
(B, nh, T, T)。 - 这个结果表示在每个注意力头上,不同序列位置之间的点积注意力分数。
- 查询向量
2. 举例说明
假设:
- 批量大小
B = 1(只有一个样本)。 - 注意力头数量
nh = 1(只有一个头)。 - 序列长度
T = 3(序列中有 3 个时间步)。 - 每个注意力头的特征维度
hs = 2(每个向量的特征长度为 2)。
输入张量 q 和 k:
-
查询向量
q的形状为(1, 1, 3, 2):q = torch.tensor([[[[1, 0],[0, 1],[1, 1]]]]) -
键向量
k的形状为(1, 1, 3, 2):k = torch.tensor([[[[1, 0],[1, 1],[0, 1]]]])
计算 k.transpose(-2, -1):
将 k 的最后两维转置,形状从 (1, 1, 3, 2) 变为 (1, 1, 2, 3):
k_transposed = torch.tensor([[[[1, 1, 0],[0, 1, 1]]]])
计算 q @ k.transpose(-2, -1):
执行矩阵乘法,将 q 的最后两维 (3, 2) 与 k_transposed 的前两维 (2, 3) 相乘,结果形状为 (1, 1, 3, 3)。
矩阵乘法过程(以第一批次和第一注意力头为例):
- 第一行(第一个时间步与所有时间步的点积):
点积 = [ 1 0 ] ⋅ [ 1 1 0 0 1 1 ] = [ 1 1 0 ] \text{点积} = \begin{bmatrix} 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 0 \end{bmatrix} 点积=[10]⋅[101101]=[110] - 第二行(第二个时间步与所有时间步的点积):
点积 = [ 0 1 ] ⋅ [ 1 1 0 0 1 1 ] = [ 0 1 1 ] \text{点积} = \begin{bmatrix} 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 1 \end{bmatrix} 点积=[01]⋅[101101]=[011] - 第三行(第三个时间步与所有时间步的点积):
点积 = [ 1 1 ] ⋅ [ 1 1 0 0 1 1 ] = [ 1 2 1 ] \text{点积} = \begin{bmatrix} 1 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 2 & 1 \end{bmatrix} 点积=[11]⋅[101101]=[121]
最终得到的注意力分数矩阵为:
att = torch.tensor([[[[1, 1, 0],[0, 1, 1],[1, 2, 1]]]])
形状为 (1, 1, 3, 3)。
3. 总结
q @ k.transpose(-2, -1)是通过矩阵乘法计算序列中每个时间步之间的点积相似性。- 结果形状
(B, nh, T, T):- 表示在每个注意力头中,序列中每个位置(行)对其他位置(列)的相似性。
- 用途:这是多头注意力机制中用于计算注意力权重(attention scores)的核心步骤,下一步通过 softmax 函数,将这些分数归一化为概率分布,表示不同时间步之间的相关性。
在多头自注意力机制中,时间步(Time Step)指的是序列中的每个位置或词的表示(embedding)。如果用一句话 “how are you” 来解析,每个时间步就对应一个单词的表示,例如 “how” 是第一个时间步,“are” 是第二个时间步,“you” 是第三个时间步。
【4】 通过 “how are you” 来解析时间步和矩阵乘法**
1. 序列与时间步的定义
- 句子 “how are you” 可以看作一个序列,长度为 3(T = 3)。
- 每个单词都会被编码成一个向量(embedding),向量的维度为
hs(head size,比如 2)。 - 这意味着,“how” 的表示是一个二维向量,“are” 和 “you” 也各自是二维向量。
假设以下是编码后的表示:
"how" = [1, 0] # 第一个时间步
"are" = [0, 1] # 第二个时间步
"you" = [1, 1] # 第三个时间步
这些向量会形成矩阵 ( q q q ) 和 ( k k k ),它们的形状都是 ( ( B , n h , T , h s ) (B, nh, T, hs) (B,nh,T,hs) ),这里我们假设批次大小 ( B = 1 B = 1 B=1 ),头的数量 ( n h = 1 nh = 1 nh=1 ),所以 ( q q q ) 和 ( k k k ) 的形状为 ( ( 1 , 1 , 3 , 2 ) (1, 1, 3, 2) (1,1,3,2) )。
2. 键向量 ( k k k ) 和转置 ( k . t r a n s p o s e ( − 2 , − 1 ) k.transpose(-2, -1) k.transpose(−2,−1) )
键向量 ( k k k ) 的矩阵如下(对应 “how”, “are”, “you” 的表示):
k = [[1, 0], # "how"[1, 1], # "are"[0, 1] # "you"
]转置后(交换最后两维),矩阵变为:
k . t r a n s p o s e ( − 2 , − 1 ) = [ 1 1 0 0 1 1 ] k.transpose(-2, -1) = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \end{bmatrix} k.transpose(−2,−1)=[101101]
3. 查询向量 ( q q q ) 的矩阵表示
查询向量 ( q q q ) 的矩阵如下(也对应 “how”, “are”, “you” 的表示):
q = [[1, 0], # "how"[0, 1], # "are"[1, 1] # "you"
]4. 矩阵乘法 ( q @ k.transpose(-2, -1) ) 的计算
矩阵乘法的目的是计算每个时间步与序列中其他时间步之间的相似性,通过点积来完成。以下是每一行的具体计算:
-
第一个时间步(“how”)与所有时间步的点积:
点积 = [ 1 0 ] ⋅ [ 1 1 0 0 1 1 ] = [ 1 1 0 ] \text{点积} = \begin{bmatrix} 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 0 \end{bmatrix} 点积=[10]⋅[101101]=[110]- “how” 与 “how” 的相似性为 ( 1 )。
- “how” 与 “are” 的相似性为 ( 1 )。
- “how” 与 “you” 的相似性为 ( 0 )。
-
第二个时间步(“are”)与所有时间步的点积:
点积 = [ 0 1 ] ⋅ [ 1 1 0 0 1 1 ] = [ 0 1 1 ] \text{点积} = \begin{bmatrix} 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 1 \end{bmatrix} 点积=[01]⋅[101101]=[011]- “are” 与 “how” 的相似性为 ( 0 )。
- “are” 与 “are” 的相似性为 ( 1 )。
- “are” 与 “you” 的相似性为 ( 1 )。
-
第三个时间步(“you”)与所有时间步的点积:
点积 = [ 1 1 ] ⋅ [ 1 1 0 0 1 1 ] = [ 1 2 1 ] \text{点积} = \begin{bmatrix} 1 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 2 & 1 \end{bmatrix} 点积=[11]⋅[101101]=[121]- “you” 与 “how” 的相似性为 ( 1 )。
- “you” 与 “are” 的相似性为 ( 2 )。
- “you” 与 “you” 的相似性为 ( 1 )。
5. 最终的注意力分数矩阵
矩阵乘法结果是一个 ( 3 × 3 3 \times 3 3×3 ) 的矩阵,表示序列中每个时间步之间的点积分数:
Attention Scores (未归一化) = [ 1 1 0 0 1 1 1 2 1 ] \text{Attention Scores (未归一化)} = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 2 & 1 \end{bmatrix} Attention Scores (未归一化)= 101112011
- 第一行表示 “how” 与其他时间步的相似性。
- 第二行表示 “are” 与其他时间步的相似性。
- 第三行表示 “you” 与其他时间步的相似性。
6. 总结
在 “how are you” 这句话中:
- 每个时间步(单词)都会被表示为一个向量。
- 通过查询向量 ( q q q ) 和键向量 ( k k k ) 的点积计算出序列中每个位置的相似性。
- 注意力分数矩阵中的每一行表示一个单词与其他单词之间的关系。
- 这些分数随后会被归一化(通过 softmax),作为多头注意力机制的权重。
参考
[1] 手撕 MHA,阿里的一面问的真是太细了
后记
2024年12月25日13点18分于上海,在GPT4o大模型辅助下完成。
相关文章:
 函数:以多头注意力机制(Multi-Head Attention)为例 (中英双语))
深入理解 PyTorch 的 view() 函数:以多头注意力机制(Multi-Head Attention)为例 (中英双语)
深入理解 PyTorch 的 view() 函数:以多头注意力机制(Multi-Head Attention)为例 在深度学习模型的实现中,view() 是 PyTorch 中一个非常常用的张量操作函数,它能够改变张量的形状(shape)而不改…...

使用PHP函数 “setcookie“ 设置cookie
在网站开发中,cookie是一种非常常用的技术,它用于在用户的浏览器中存储少量的数据,以便在不同页面之间传递信息。PHP提供了一个名为 "setcookie" 的函数,用于设置cookie的值和属性。在本文中,我们将学习如何…...

redis优化
在高并发、高性能、高可用系统中,Redis 的优化至关重要。以下是一些在面试中可以详细说明的 Redis 优化策略,以及具体的实践经验和技术亮点: 1. 数据模型与结构设计优化 使用合适的数据结构 :根据业务需求选择合适的 Redis 数据结…...

数据分析的革命——解读云数据库 SelectDB 版的力量
在当今数据驱动的时代,实时数据分析已成为企业决策中的关键一环。如何在海量数据中快速找到核心价值,如何让决策者在毫秒间洞悉变化,这不仅考验着企业的技术能力,也对基础设施提出了新的要求。云数据库 SelectDB 版,正…...
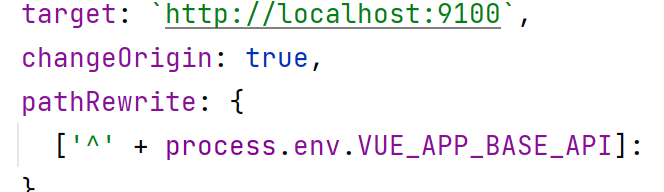
Ngnix介绍、安装、实战及用法!!!
一、Nginx简介 1、Nginx概述 Nginx (“engine x”) 是一个高性能的 HTTP 和 反向代理服务器,特点是占有内存少,并发能力强,能经受高负载的考验,有报告表明能支持高达 50,000 个并发连接数 。 2、正向代理 正向代理:如果把局…...

算法基础一:冒泡排序
一、冒泡排序 1、定义 冒泡排序(英语:Bubble Sort)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序(如从大到小、首字母从A到Z)错误就把他们交换过来。 …...
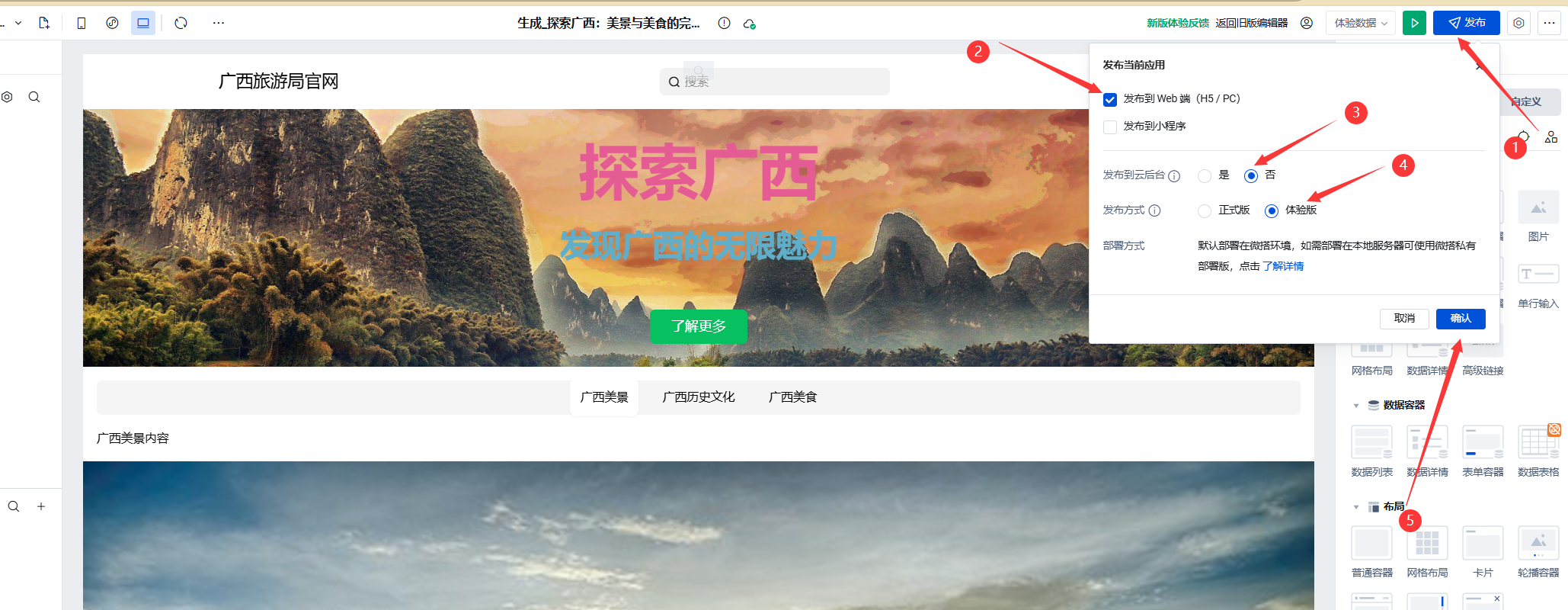
云开发实战教程:手把手教你高效开发应用
声明:本文仅供实践教学使用,没有任何打广告成分 目录 1.引言 2.云开发 Copilot介绍 云开发 Copilot 的功能与特点 3.环境准备 步骤一登录账号 步骤二新建环境 4.开发实践 4.1AI 生成低代码应用 4.2AI 生成低代码页面/区块 4.3AI 优化低代码组件…...

Git基本操作快速入门(30min)
Git基本操作快速入门(30min) 文章目录 Git基本操作快速入门(30min)1. 建立本地仓库2. 本地仓库链接到远端仓库3. 将本地仓库推送到远端4. Git常用命令 作为一名程序员,使用Github来进行代码的版本管理是必修课…...

VS Code AI开发之Copilot配置和使用详解
随着AI开发工具的迅速发展,GitHub Copilot在Cursor、Winsuf、V0等一众工具的冲击下,推出了免费版本。接下来,我将为大家介绍GitHub Copilot的配置和使用方法。GitHub Copilot基于OpenAI Codex模型,旨在为软件开发者提供智能化的代…...

QT中使用OpenGL function
1.前言 QT做界面编程很方便,QTOpenGL的使用也很方便,因为QT对原生的OpenGL API进行了面向对象化的封装。 如: 函数:initializeOpenGLFunctions()...... 类:QOpenGLVertexArrayObject、QOpenGLBuffer、QOpenGLShader…...

STM32-笔记16-定时器中断点灯
一、实验目的 使用定时器 2 进行中断点灯,500ms LED 灯翻转一次。 二,定时器溢出时间计算 Tout:定时器溢出时间 Ft:定时器的时钟源频率 ARR:自动重装载寄存器的值(可设置ARR从0开始,但是计数到…...

Live555、FFmpeg、GStreamer介绍
Live555、FFmpeg 和 GStreamer 都是处理流媒体和视频数据的强大开源框架和工具,它们广泛应用于实时视频流的推送、接收、处理和播放。每个框架有不同的设计理念、功能特性以及适用场景。下面将详细分析这三个框架的作用、解决的问题、适用场景、优缺点,并…...
 用法)
oracle基础:理解 Oracle SQL 中的 WHERE 后的 (+) 用法
在使用 Oracle 数据库进行 SQL 查询时,可能会遇到 WHERE 子句后带有 () 的语法。这是 Oracle 专有的外连接(Outer Join)表示法。虽然现代 SQL 标准推荐使用 LEFT JOIN 和 RIGHT JOIN 语法,但在某些遗留系统中,这种写法…...

【linux】进程间通信(IPC)——匿名管道,命名管道与System V内核方案的共享内存,以及消息队列和信号量的原理概述
目录 ✈必备知识 进程间通信概述 🔥概述 🔥必要性 🔥原理 管道概述 🔥管道的本质 🔥管道的相关特性 🔥管道的同步与互斥机制 匿名管道 🔥系统调用接口介绍 🔥内核原理 …...

【深度学习】卷积网络代码实战ResNet
ResNet (Residual Network) 是由微软研究院的何凯明等人在2015年提出的一种深度卷积神经网络结构。ResNet的设计目标是解决深层网络训练中的梯度消失和梯度爆炸问题,进一步提高网络的表现。下面是一个ResNet模型实现,使用PyTorch框架来展示如何实现基本的…...

org.apache.zookeeper.server.quorum.QuorumPeerMain
QuorumPeerMain源代码 package org.apache.zookeeper.server.quorum;import java.io.IOException; import javax.management.JMException; import javax.security.sasl.SaslException; import org.apache.yetus.audience.InterfaceAudience; import org.apache.zookeeper.audi…...

oscp学习之路,Kioptix Level2靶场通关教程
oscp学习之路,Kioptix Level2靶场通关教程 靶场下载:Kioptrix Level 2.zip 链接: https://pan.baidu.com/s/1gxVRhrzLW1oI_MhcfWPn0w?pwd1111 提取码: 1111 搭建好靶场之后输入ip a看一下攻击机的IP。 确定好本机IP后,使用nmap扫描网段&…...

SkyWalking java-agent 是如何工作的,自己实现一个监控sql执行耗时的agent
Apache SkyWalking 是一个开源的应用性能监控 (APM) 工具,支持分布式系统的追踪、监控和诊断。SkyWalking Agent 是其中的一个重要组件,用于在服务端应用中收集性能数据和追踪信息,并将其发送到 SkyWalking 后端服务器进行处理和展示。 SkyW…...

每天40分玩转Django:Django表单集
Django表单集 一、知识要点概览表 类别知识点掌握程度要求基础概念FormSet、ModelFormSet深入理解内联表单集InlineFormSet、BaseInlineFormSet熟练应用表单集验证clean方法、验证规则熟练应用自定义配置extra、max_num、can_delete理解应用动态管理JavaScript动态添加/删除表…...

查看vue的所有版本号和已安装的版本
1.使用npm查看Vue的所有版本: npm view vue versions2.查看项目中已安装的 Vue.js 版本 npm list vue...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
