当算法遇到线性代数(四):奇异值分解(SVD)
SVD分解的理论与应用
线性代数系列相关文章(置顶)
1.当算法遇到线性代数(一):二次型和矩阵正定的意义
2.当算法遇到线性代数(二):矩阵特征值的意义
3.当算法遇到线性代数(三):实对称矩阵
4.当算法遇到线性代数(四):奇异值分解(SVD)
引言
奇异值分解(Singular Value Decomposition, SVD)是线性代数中一个极为重要的概念,它在数据科学、机器学习、信号处理等多个领域有着广泛的应用。本文将详细介绍SVD的背景、定义、性质、具体过程以及其在不同领域的应用,并总结其重要性。

一、背景
SVD的概念最早可以追溯到19世纪末期,当时数学家们开始研究矩阵的特征值和特征向量问题。然而,直到20世纪中期,随着计算机技术的发展,SVD才逐渐成为一种实用且高效的工具。特别是在图像压缩、推荐系统等领域,SVD因其能够揭示数据内部结构的能力而备受青睐。
二、定义与概念
对于任意 m × n m \times n m×n 的实矩阵 A A A,存在两个正交矩阵 U U U 和 V V V,以及一个非负对角矩阵 Σ \Sigma Σ,使得:
A = U Σ V T A = U \Sigma V^T A=UΣVT
其中:
- U U U 是一个 m × m m \times m m×m 的正交矩阵,称为左奇异向量。
- V V V 是一个 n × n n \times n n×n 的正交矩阵,称为右奇异向量。
- Σ \Sigma Σ 是一个 m × n m \times n m×n 的对角矩阵,对角元素为非负实数,称为奇异值,通常按降序排列。
三、性质
SVD具有以下重要性质:
- 唯一性:如果 A A A 的所有奇异值都是不同的,则 U U U 和 V V V 是唯一的(忽略符号变化)。
- 最优低秩近似:根据Eckart–Young定理,截断后的SVD提供了原矩阵的最佳低秩近似。
- 数值稳定性:SVD算法相对稳定,尤其适用于处理病态矩阵或接近奇异的矩阵。
- 几何解释:SVD可以被理解为一系列旋转、缩放和平移操作,这些操作将原始空间中的点映射到新坐标系下。
由于上述性质,奇异值分解(SVD)具有许多显著的好处,这些优点使得它在多个学科和技术领域中成为一种极为有用的工具。以下是SVD的主要好处:
1. 数值稳定性
- 处理病态矩阵:对于接近奇异或病态的矩阵,直接求解线性系统可能会导致严重的数值误差。而SVD提供了一种更加稳定的方法来处理这类问题。
- 避免过拟合:在机器学习和统计建模中,SVD可以帮助防止模型对训练数据的过度拟合,从而提高泛化能力。
2. 最优低秩近似
- 数据压缩:通过保留前几个最大的奇异值及其对应的左、右奇异向量,可以得到原矩阵的最佳低秩近似。这种方法不仅减少了存储需求,还能够去除噪声,保持数据的核心特征。
- 降维:例如在主成分分析(PCA)中,SVD用于将高维数据投影到低维空间,同时尽可能地保留原始数据的方差信息。

3. 几何与物理意义明确
- 变换解释:SVD可以被直观地理解为一系列旋转、缩放和平移操作,这些操作将原始空间中的点映射到新坐标系下。这种几何解释有助于更好地理解数据结构和模式。
- 正交基底:SVD提供了两组正交基底,分别对应于输入空间和输出空间,这使得计算过程更加清晰且易于实现。
4. 理论洞察力
- 揭示内在结构:SVD能够揭示数据背后的潜在结构,这对于探索数据特性、发现隐藏模式非常有帮助。
- 理论研究:在数学、物理学等多个基础科学领域,SVD为理论分析提供了强有力的支持,促进了新算法和理论的发展。
四、举个🌰
1. 矩阵SVD计算
考虑一个 3 × 2 3 \times 2 3×2 的矩阵 A A A:
A = [ 1 2 2 3 3 4 ] A = \begin{bmatrix} 1 & 2 \\ 2 & 3 \\ 3 & 4 \end{bmatrix} A= 123234
为了求解 A A A 的SVD,我们需要执行以下步骤:
-
计算协方差矩阵 A A T AA^T AAT 和 A T A A^TA ATA。
- A A T = [ 5 8 11 8 13 18 11 18 25 ] AA^T = \begin{bmatrix} 5 & 8 & 11 \\ 8 & 13 & 18 \\ 11 & 18 & 25 \end{bmatrix} AAT= 581181318111825
- A T A = [ 14 20 20 29 ] A^TA = \begin{bmatrix} 14 & 20 \\ 20 & 29 \end{bmatrix} ATA=[14202029]
-
找到 A T A A^TA ATA 的特征值和特征向量。
- 特征值: σ 1 2 ≈ 43.6 \sigma_1^2 \approx 43.6 σ12≈43.6, σ 2 2 ≈ 0.37 \sigma_2^2 \approx 0.37 σ22≈0.37
- 特征向量: v 1 ≈ [ − 0.65 − 0.76 ] v_1 \approx \begin{bmatrix} -0.65 \\ -0.76 \end{bmatrix} v1≈[−0.65−0.76], v 2 ≈ [ 0.76 − 0.65 ] v_2 \approx \begin{bmatrix} 0.76 \\ -0.65 \end{bmatrix} v2≈[0.76−0.65]
-
构造 Σ \Sigma Σ,并将特征值开平方根得到奇异值。
- Σ = [ 43.6 0 0 0.37 0 0 ] \Sigma = \begin{bmatrix} \sqrt{43.6} & 0 \\ 0 & \sqrt{0.37} \\ 0 & 0 \end{bmatrix} Σ= 43.60000.370
-
找到 A A T AA^T AAT 的特征值和特征向量。
- 特征值:同上
- 特征向量: u 1 ≈ [ − 0.38 − 0.57 − 0.76 ] u_1 \approx \begin{bmatrix} -0.38 \\ -0.57 \\ -0.76 \end{bmatrix} u1≈ −0.38−0.57−0.76 , u 2 ≈ [ − 0.92 0.38 − 0.07 ] u_2 \approx \begin{bmatrix} -0.92 \\ 0.38 \\ -0.07 \end{bmatrix} u2≈ −0.920.38−0.07
-
验证结果:
- A = U Σ V T ≈ [ − 0.38 − 0.92 ∗ − 0.57 0.38 ∗ − 0.76 − 0.07 ∗ ] [ 43.6 0 0 0.37 0 0 ] [ − 0.65 − 0.76 0.76 − 0.65 ] A = U \Sigma V^T \approx \begin{bmatrix} -0.38 & -0.92 & * \\ -0.57 & 0.38 & * \\ -0.76 & -0.07 & * \end{bmatrix} \begin{bmatrix} \sqrt{43.6} & 0 \\ 0 & \sqrt{0.37} \\ 0 & 0 \end{bmatrix} \begin{bmatrix} -0.65 & -0.76 \\ 0.76 & -0.65 \end{bmatrix} A=UΣVT≈ −0.38−0.57−0.76−0.920.38−0.07∗∗∗ 43.60000.370 [−0.650.76−0.76−0.65]
注意:这里的 ∗ * ∗ 表示不相关的第三列元素,因为 A A A 只有两列。
2. 低秩近似
使用SVD对100x100物品相似度矩阵进行低秩近似的具体表示,我们将通过数学符号和公式来展示如何使用奇异值分解(SVD)对一个 100 × 100 100 \times 100 100×100 的物品相似度矩阵 A A A 进行低秩近似,并保留前5个最大的奇异值。
步骤 1: 准备数据
假设我们有一个 100 × 100 100 \times 100 100×100 的相似度矩阵 A A A,其中每个元素 a i j a_{ij} aij 表示物品 i i i 和物品 j j j 之间的相似度。由于这是一个相似度矩阵,它是对称的,即 A = A T A = A^T A=AT。
步骤 2: 计算 SVD 分解
根据SVD理论,我们可以将矩阵 A A A 分解为:
A = U Σ V T A = U \Sigma V^T A=UΣVT
其中:
- U U U 是一个 100 × 100 100 \times 100 100×100 的正交矩阵,称为左奇异向量矩阵。
- Σ \Sigma Σ 是一个 100 × 100 100 \times 100 100×100 的对角矩阵,包含按降序排列的奇异值。
- V V V 是一个 100 × 100 100 \times 100 100×100 的正交矩阵,称为右奇异向量矩阵。
步骤 3: 构建低秩近似矩阵
为了构建低秩近似矩阵 A 5 A_5 A5,我们只保留前5个最大的奇异值及其对应的左、右奇异向量。具体来说:
- 选择前5个奇异值: σ 1 , σ 2 , σ 3 , σ 4 , σ 5 \sigma_1, \sigma_2, \sigma_3, \sigma_4, \sigma_5 σ1,σ2,σ3,σ4,σ5
- 选择对应的左奇异向量: u 1 , u 2 , u 3 , u 4 , u 5 u_1, u_2, u_3, u_4, u_5 u1,u2,u3,u4,u5,构成 U 5 U_5 U5,这是一个 100 × 5 100 \times 5 100×5 的矩阵。
- 选择对应的右奇异向量: v 1 , v 2 , v 3 , v 4 , v 5 v_1, v_2, v_3, v_4, v_5 v1,v2,v3,v4,v5,构成 V 5 V_5 V5,这也是一个 100 × 5 100 \times 5 100×5 的矩阵。
因此,新的对角矩阵 Σ 5 \Sigma_5 Σ5 将是一个 5 × 5 5 \times 5 5×5 的矩阵,仅包含前5个奇异值:
Σ 5 = [ σ 1 0 0 0 0 0 σ 2 0 0 0 0 0 σ 3 0 0 0 0 0 σ 4 0 0 0 0 0 σ 5 ] \Sigma_5 = \begin{bmatrix} \sigma_1 & 0 & 0 & 0 & 0 \\ 0 & \sigma_2 & 0 & 0 & 0 \\ 0 & 0 & \sigma_3 & 0 & 0 \\ 0 & 0 & 0 & \sigma_4 & 0 \\ 0 & 0 & 0 & 0 & \sigma_5 \end{bmatrix} Σ5= σ100000σ200000σ300000σ400000σ5
步骤 4: 构造低秩近似矩阵 A 5 A_5 A5
使用 U 5 U_5 U5, Σ 5 \Sigma_5 Σ5,和 V 5 V_5 V5 来构造低秩近似矩阵 A 5 A_5 A5:
A 5 = U 5 Σ 5 V 5 T A_5 = U_5 \Sigma_5 V_5^T A5=U5Σ5V5T
这里:
- U 5 U_5 U5 是 100 × 5 100 \times 5 100×5 的矩阵,由 U U U 的前五列组成。
- Σ 5 \Sigma_5 Σ5 是 5 × 5 5 \times 5 5×5 的对角矩阵,包含前五个奇异值。
- V 5 V_5 V5 是 100 × 5 100 \times 5 100×5 的矩阵,由 V V V 的前五列组成。
结果分析
比较原始矩阵 A A A 和低秩近似矩阵 A 5 A_5 A5:
- 误差评估:可以通过计算 Frobenius 范数误差 ∥ A − A 5 ∥ F \|A - A_5\|_F ∥A−A5∥F 来评估低秩近似的效果。
- 可视化对比:可以绘制原始矩阵 A A A 和低秩近似矩阵 A 5 A_5 A5 的热图,直观地观察两者之间的差异。
通过这个过程,我们展示了如何使用SVD对一个 100 × 100 100 \times 100 100×100 的物品相似度矩阵进行低秩近似,并保留前5个最大的奇异值。这种方法不仅减少存储需求,还能够有效地处理大规模数据集,同时保持了数据的核心特征。通过选择适当的 k k k,可以在保持足够精度的同时显著减少计算复杂度。
五、应用
数学领域应用
- 低秩近似:通过保留前几个最大的奇异值及其对应的奇异向量,可以实现矩阵的有效压缩,同时保持尽可能多的信息。
- 最小二乘问题:SVD可用于解决超定系统的最小二乘解,提供了一种稳健的方法来估计未知参数。
机器学习与深度学习应用
- 主成分分析 (PCA):SVD是PCA的核心算法之一,用于降维和特征提取。
- 大模型 LoRA 微调:LoRA 的关键在于引入低秩矩阵 A ∈ R m × r A \in \mathbb{R}^{m \times r} A∈Rm×r 和 B ∈ R r × n B \in \mathbb{R}^{r \times n} B∈Rr×n 来近似更新原始权重矩阵 W ∈ R m × n W \in \mathbb{R}^{m \times n} W∈Rm×n。
- 推荐系统:基于用户-物品评分矩阵的协同过滤方法中,SVD可以用来预测未观察到的评分并做出个性化推荐。
- 图像处理:如图像压缩、去噪等任务中,利用SVD去除冗余信息,提高效率。
其他领域应用
- 信号处理:用于频谱分析、滤波器设计等方面,帮助提取信号的主要成分。
- 自然语言处理:例如主题模型LDA可以通过SVD进行优化,以更好地捕捉文档之间的关系。
- 控制系统:在状态估计、模型简化等环节中,SVD有助于构建更精确和稳定的控制器。
六、总结
综上所述,SVD作为一种强大的数学工具,在多个学科和技术领域都展现出了巨大的价值。从理论上讲,它提供了深刻的洞察力,使我们能够理解和操作复杂的数据集;而在实践中,SVD不仅简化了许多复杂的计算任务,还提高了算法的性能和可靠性。无论是在学术研究还是工业应用中,掌握SVD的基本原理及其应用技巧都是非常有益的。
相关文章:

当算法遇到线性代数(四):奇异值分解(SVD)
SVD分解的理论与应用 线性代数系列相关文章(置顶) 1.当算法遇到线性代数(一):二次型和矩阵正定的意义 2.当算法遇到线性代数(二):矩阵特征值的意义 3.当算法遇到线性代数࿰…...

SASS 简化代码开发的基本方法
概要 本文以一个按钮开发的实例,介绍如何使用SASS来简化CSS代码开发的。 代码和实现 我们希望通过CSS开发下面的代码样式,从样式来看,每个按钮的基本样式相同,就是颜色不同。 如果按照传统的方式开发,需要开发btn &…...

40.TryParse尝试转化为int类型 C#例子
也许这个时候学有点晚,但是不管怎样都学了 尝试转化,不能转化就返回bool类型的假 它会直接给括号里面的int类型赋值 代码: using System; using System.Timers; public class Program {static void Main(){int a;bool i;while (true){Get…...

【微服务】2、网关
Spring Cloud微服务网关技术介绍 单体项目拆分微服务后的问题 服务地址问题:单体项目端口固定(如黑马商城为8080),拆分微服务后端口各异(如购物车808、商品8081、支付8086等)且可能变化,前端难…...
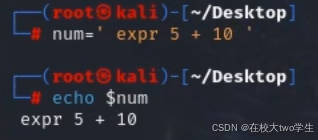
红队-shell编程篇(上)
声明 通过学习 泷羽sec的个人空间-泷羽sec个人主页-哔哩哔哩视频,做出的文章如涉及侵权马上删除文章 笔记的只是方便各位师傅学习知识,以下网站只涉及学习内容,其他的都与本人无关,切莫逾越法律红线,否则后果自负 一、建立Shell文件 1. Shell简介 Shell是一种命令行界面&am…...

电子价签会是零售界的下一个主流?【新立电子】
电子价签,作为一种能够替代传统纸质标签的数字显示屏,已经在零售行业中展现出其巨大的潜力。它具有实时更新、集中管理、高效节能的特点,实现价格的实时更新,大大减少更新价格的工作量和时间。为消费者带来更加便捷、准确的购物体…...

5 分布式ID
这里讲一个比较常用的分布式防重复的ID生成策略,雪花算法 一个用户体量比较大的分布式系统必然伴随着分表分库,分机房部署,单体的部署方式肯定是承载不了这么大的体量。 雪花算法的结构说明 如下图所示: 雪花算法组成 从上图我们可以看…...

SpringBoot | @Autowired 和 @Resource 的区别及原理分析
关注:CodingTechWork 引言 在Spring框架中,Autowired 和 Resource 是两种常用的依赖注入注解,它们都用于自动装配Bean,简化了开发者手动创建和管理Bean的繁琐工作。然而,它们的实现机制和使用方式有所不同。理解这两者…...
)
『SQLite』解释执行(Explain)
摘要:本节主要讲解SQL的解释执行:Explain。 在 sqlite 语句之前,可以使用 “EXPLAIN” 关键字或 “EXPLAIN QUERY PLAN” 短语,用于描述表查询的细节。 基本语法 EXPLAIN 语法: EXPLAIN [SQLite Query]EXPLAIN QUER…...

0基础学前端-----CSS DAY12
视频参考:B站Pink老师 今天是CSS学习的第十二天,今天开始的笔记对应Pink老师课程中的CSS第七天的内容。 本节重点:CSS高级技巧 本章目录 本节目标1. 精灵图1.1 为什么需要精灵图1.2 精灵图使用案例:拼出自己的名字 2. 字体图标2.…...

(概率论)无偏估计
参考文章:(15 封私信 / 51 条消息) 什么是无偏估计? - 知乎 (zhihu.com) 首先,第一个回答中,马同学图解数学讲解得很形象, 我的概括是:“注意,有一个总体的均值u。然后,如果抽样n个&…...

Minio-Linux-安装
文章目录 1.Linux安装1.下载源码包2.上传到/usr/local/minio1.进入目录2.上传 3.开放执行权限4.创建minio文件存储目录及日志目录5.编写启动的shell脚本1.脚本编写2.赋予执行权限 6.启动!1.执行run脚本2.查看日志3.开放9001和9000端口1.服务器2.安全组3.访问&#x…...

利用Java爬取1688商品详情API接口:技术与应用指南
引言 1688作为中国领先的B2B电子商务平台,拥有海量的商品信息。对于商家和市场研究人员来说,能够从1688获取商品详情信息,对于市场分析、竞品研究等具有重要价值。本文将详细介绍如何使用Java编写爬虫程序,以合法、高效的方式获取…...

基于MATLAB的汽车热管理模型构建
一、引言 汽车热管理系统对汽车性能、部件寿命及驾乘体验至关重要。它能确保发动机、电池等关键部件在适宜温度工作。MATLAB 功能强大,为构建高精度热管理模型提供有效途径,助力优化系统设计与控制策略。 二、汽车热管理系统构成 2.1 发动机冷却系统&…...
)
LRU(1)
LRU是"Least Recently Used"(最近最少使用)的缩写,它是一种常用的页面置换算法和缓存淘汰策略。当计算机系统的内存或缓存资源有限时,LRU算法根据的历史访问记录来决定哪些数据应该被保留在内存或缓存中,哪些被淘汰。其核心思想是“…...

VSCode 使用鼠标滚轮控制字体
一、 文件 | 首选项 | 设置 二、单击在 settings.json中编辑 "editor.mouseWheelZoom": true 注注注意:保存哦!ctrlS 三、测试 按住ctrl鼠标滚轮,控制字体大小...

数据库(3)--针对列的CRUD操作
1.Create 新增 语法: insert into 表名 (列名)values (列)... 创建一个学生表用于演示: create table if not exists student( id bigint comment 编号, name varchar(20) comment 姓名 ); 1.1直接增加…...

【Linux】记录一下考RHCE的学习过程(七)
年底了,公司接的北京地铁轨道交通的项目做不完了,一百多列地铁的设备都得调,派我出差了几周,这几天才回来,出差累死了实在是没办法更新。(YOASOBI的二开票还没抢到ToT,哭死,看看回滚…...

【顶刊TPAMI 2025】多头编码(MHE)之极限分类 Part 1:背景动机
目录 1 简单概括2 几个重要发现3 主要贡献4 背景知识5 方法简介 论文:Multi-Head Encoding for Extreme Label Classification 作者:Daojun Liang, Haixia Zhang, Dongfeng Yuan and Minggao Zhang 单位:山东大学 代码:https://gi…...

使用hardhat进行合约测试
演示源码:hardhat-demo: 演示基于hardhat的HelloWord合约测试案例。 环境 NodeJs 创建工程 1.创建一个hardhat工程根目录(hardhat-demo),然后进入该目录执行。 npx hardhat执行该命令,会进行hardhat工程初始化。 提示我们是否安装该版本h…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
