(leetcode算法题)769. 最多能完成排序的块

Q1. 是否能用贪心算法?为什么?
先预设一个策略,每当当前的nums[i]满足可以 "成块",就直接让这个数成块,也就是说之后的遍历过程中不会将这个数在考虑到自己的块内,
"成块" 是指只要只需要将nums[i]放到前面的某个子数组的尾部,然后将这个子数组进行排序,就能得到一个拥有连续自然数的子数组,就称为成块
能够使用谈心算法是因为有如下规律
规律1. 以nums[i]为结尾的成块的子数组,其中的最大值不能小于 i
反证法:假设nums[i]为结尾的成块的子数组,其中最大值小于 i
那么对这个子数组进行排序后,最后一个值即为maxval,且其下标标定位i
子数组最开始的那个下标设为j, 那么子数组中应该有 i - j + 1个元素
又根据成块的定义,这里将会缺少自然数填满i - j + 1个位置矛盾
故,想要成块,子数组的最大值不能小于 i
下面以图示的方法进一步说明,假设红线前的0 1 2已经成块了

如果 nums[7] < 7 那么一定不能成块,因为此时只能有 6 5 4 3 2 1 0 能放入这8个黑框中,
规律2. 以nums[i]为结尾的成块的子数组,其中的最大值不能大于 i
证明与上面类似,矛盾之处在于如果最大值大于 i ,则将会多出来一个元素
所以要想成块只能是maxval == i
class Solution {
public:int maxChunksToSorted(vector<int>& arr) {int n = arr.size();int ret = 0;int curmax = 0;for(int i = 0; i < n; ++i){curmax = max(curmax, arr[i]);if(curmax == i){ret++;}}return ret;}
};相关文章:

(leetcode算法题)769. 最多能完成排序的块
Q1. 是否能用贪心算法?为什么? 先预设一个策略,每当当前的nums[i]满足可以 "成块",就直接让这个数成块,也就是说之后的遍历过程中不会将这个数在考虑到自己的块内, "成块" 是指只要只…...

高光谱相机的特点
光谱特性 高光谱分辨率:能将光谱范围分割成极窄的波段,光谱分辨率通常达到纳米级甚至亚纳米级,可精确捕捉到不同物质在细微光谱差异上的特征,比如可以区分不同种类的植被因叶绿素含量等差异而在光谱上的细微变化。 多波段探测&a…...

《Spring Framework实战》8:4.1.3.Bean 概述
欢迎观看《Spring Framework实战》视频教程 Spring IoC 容器管理一个或多个 bean。这些 bean 是使用 您提供给容器的配置元数据(例如,以 XML <bean/>定义的形式)。 在容器本身中,这些 bean 定义表示为BeanDefinition对象&a…...

BGP的local_preference本地优先级属性
一、BGP的local preference属性简介 1、local preference公认任意属性 当一条BGP路由器中存在多条去往同一目标网络的BGP路由时,BGP协议会对这些BGP路由属性进行比较,从而筛选出最佳到达目标网络的通达路径。本地优先属性,只在IBGP对等体之间…...

IP地址与端口号
ip地址与端口号 IP地址和端口号是网络通信中的两个重要概念,它们共同构成了网络通信的基础。 IP地址:网络世界的门牌号 定义:IP地址(Internet Protocol Address)是分配给网络设备的数字标签,用于在计算机网…...
--日志中间件)
Fastapi + vue3 自动化测试平台(2)--日志中间件
FastAPI Vue3 自动化测试平台(2)-- 日志中间件 前言 在开发和运行自动化测试平台时,日志功能是至关重要的一部分。日志不仅能帮助我们快速定位和解决问题,还能作为平台运行的记录依据,为后续分析和优化提供参考。 …...

iOS - AutoreleasePool
1. 基本数据结构 // AutoreleasePool 的基本结构 struct AutoreleasePoolPage {static pthread_key_t const key AUTORELEASE_POOL_KEY;magic_t const magic;id *next; // 指向下一个可存放对象的地址pthread_t const thread; // 所属线程AutoreleasePoolPage …...

1.CSS的复合选择器
1.1 什么是复合选择器 在CSS中,可以根据选择器的类型把选择器分为基础选择器和复合选择器,复合选择器是建立在基础选择器之上,对基础选择器进行组合形成的。 复合选择器可以更精准、更高效的选择目标元素(标签) 复…...

优质内容在个人IP运营中的重要性:以开源AI智能名片商城小程序为应用实例的深度探讨
摘要:在数字化时代,个人品牌(IP)的塑造与传播已成为各行各业提升影响力、吸引用户关注、促进商业转化的关键策略。优质内容作为连接个人IP与目标受众的桥梁,其在个人IP运营中的重要性不言而喻。本文旨在深入探讨优质内…...

Kafka性能测试
kafka是一个大数据消息队列(可以看做为缓存软件) 功能测试:能够读写数据 性能测试:1、测试生产者每秒往kafka写入的最大吞吐量 2、测试消费者每秒从kafka里获取消息最大吞吐量 硬件 3台物理机组成的kafka集群。 内存121G、24…...

解决Docker冲突问题
错误:docker-ce-cli conflicts with 2:docker-1.13.1-210.git7d71120.el7.centos.x86_64 错误:docker-ce conflicts with 2:docker-1.13.1-210.git7d71120.el7.centos.x86_64 您可以尝试添加 --skip-broken 选项来解决该问题 您可以尝试执行:…...

新手入门 React .tsx 项目:从零到实战
🚀 新手入门 React .tsx 项目:从零到实战 💻✨ 如果你是 React 新手,刚接触 .tsx 文件,不要担心!跟着这份指南,一步一步来,你很快就能上手了!👇 Ὅ…...

基于可信数据空间的企业数据要素与流通体系建设(附ppt 下载)
近期,可信数据空间会议召开。大数据系统软件国家工程研究中心总工程师王晨发表了题为《基于可信数据空间的企业数据要素与流通体系建设》主旨演讲。 篇幅限制,部分内容如下:...
C语言)
二维数组:求最大元素及其所在的行坐标及列坐标(PTA)C语言
求出NM整型数组的最大元素及其所在的行坐标及列坐标(如果最大元素不唯一,选择位置在最前面的一个)。 函数接口定义: int fun(int array[N][M]) ; 注意:函数只需靠return返回最大元素的值, 行、列坐标通过…...

WebRtc01: 课程导学、框架介绍
应用 难点 课程大纲 学习收获 涉及内容 概述 用途 学习收获...

HQChart使用教程30-K线图如何对接第3方数据44-DRAWPIE数据结构
HQChart使用教程30-K线图如何对接第3方数据44-DRAWPIE数据结构 效果图DRAWPIEHQChart代码地址后台数据对接说明示例数据数据结构说明效果图 DRAWPIE DRAWPIE是hqchart插件独有的绘制饼图函数,可以通过麦语法脚本来绘制一个简单的饼图数据。 饼图显示的位置固定在右上角。 下…...
和2维块(block)对矩阵进行求和)
【cuda学习日记】2.2 使用2维网络(grid)和2维块(block)对矩阵进行求和
在2.0中进行了用一维网格和块对一维向量进行了求和。 在2.1中例化了二维的网格和块。 接下来进行2维网络(grid)和2维块(block)对矩阵进行求和。 #include <stdio.h> #include <stdlib.h> #include <time.h> #i…...

深度学习中CUDA环境安装教程
首先说明,本人是小白,一次安装,可能有不对的地方,望包含。 安装CUDA 因为我们是深度学习,很多时候要用到gpu进行训练,所以我们需要一种方式加快训练速度。 通俗地说,CUDA是一种协助“CPU任务分…...
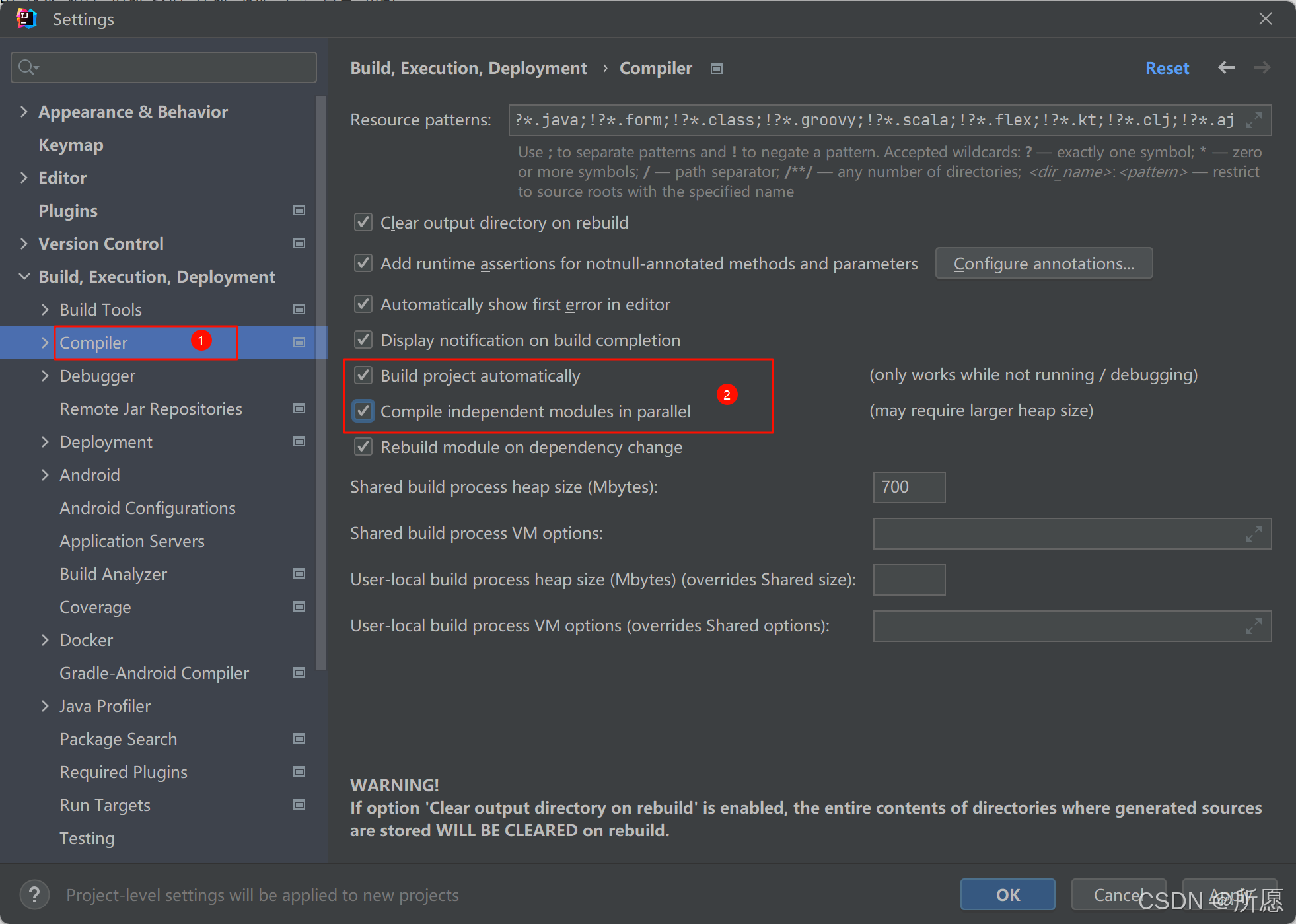
IDEA的常用设置
目录 一、显示顶部工具栏 二、设置编辑区字体按住鼠标滚轮变大变小(看需要设置) 三、设置自动导包和优化导入的包(有的时候还是需要手动导包) 四、设置导入同一个包下的类,超过指定个数的时候,合并为*&a…...

【VUE+ElementUI】通过接口下载blob流文件设置全局Loading加载进度
下载Blob流文件,并以服务形式显示文件下载进度 1、下载接口 增加 config参数,并用...config将该属性加入到请求中; xxapi.js文件中设置downloadFile下载接口 // 下载文件 export function downloadFile(data, config) {return request({ur…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
