蓝笔科技 | 超凡妈妈赋能计划-【北大生涯规划师特别企划】
12月27日,“超凡妈妈赋能计划-北大生涯规划师特别企划”在广州正式启动,据了解,本次超凡妈妈赋能计划是由广州蓝笔科技信息有限公司牵头发起并主办,中国关心下一代健康体育基金会作为公益支持单位,北京大学作为项目技术支持单位。该计划响应国家对家庭教育及女性创业的重视与支持政策,旨在发展教育公益事业,为妈妈们提供一个全新的学习与成长平台,为孩子们提供专业的升学与生涯规划指导。
会议邀请了中国关心下一代健康体育基金会副主任兼秘书长曾芝冰,北京大学生命科学学院北生英才主任曹可盈,清华大学计算机博士、深圳清华大学研究院区块链与数智化治理研发中心副主任张博,超凡妈妈项目共同发起人(原聚成股份董事长)陈其仁,蓝笔科技董事长黄泽帆,超凡妈妈项目共同发起人、蓝笔科技联合创始人王超然,超凡妈妈项目共同发起人、百万粉丝育儿博主陈小璟,凯丽思医学美容集团执行董事易琛善,太子家居直营公司总经理帅博文等嘉宾参加了本次会议。

活动合影
超凡妈妈超强赋能
会议伊始,中国关心下一代健康体育基金会副主任兼秘书长曾芝冰首先做开场致辞。他表示,超凡妈妈项目积极响应了社会对家庭教育和女性创业的呼声,不仅是一项家庭教育项目,更是一项具有深远社会意义的教育公益事业。青少年是国家未来的希望,时代进步的重要力量,而家庭教育,是青少年健康发展最关键的一环。中国关心下一代健康体育基金会一直秉承着促进下一代健康成长和全面发展的使命,呼吁更多社会力量参与,共同助力下一代成长,投入超凡妈妈赋能计划的公益事业中,为她们提供实现自我价值和社会价值的广阔空间。

中国关心下一代健康体育基金会副主任兼秘书长 曾芝冰
随后,北京大学生命科学学院北生英才主任曹可盈上台致辞。她提出,教育的核心是用一个灵魂去唤醒另一个灵魂的过程,北京大学作为项目技术支持单位,将蓝笔科技指定为“生涯规划师证书项目”独家合作伙伴,旨在通过系统的培训和认证,培养一批具有专业素养和实战经验的生涯规划师,为广大学生和家长提供专业的学业报考和职业规划服务。

北京大学生命科学学院北生英才主任 曹可盈
特邀嘉宾清华大学计算机博士、深圳清华大学研究院区块链与数智化治理研发中心副主任张博在《AI时代教育产业数智化与高质量发展》演讲中表示,在人工智能时代,家庭教育正经历着深刻的变革,这些变化不仅为家庭教育带来了新的机遇,也带来了挑战,我们都应该关注人工智能赋能家庭教育的发展。

清华大学计算机博士、深圳清华大学研究院区块链与数智化治理研发中心副主任 张博
蓝笔科技董事长黄泽帆在致辞中表示,蓝笔科技是北京大学生涯规划师证书唯一承接单位,致力于通过“超凡妈妈项目”为妈妈们提供平台价值赋能,让妈妈真正成为自己和孩子的光,为女性创业和再就业开辟新天地,更是为了给孩子们的未来描绘光明的蓝图。

蓝笔科技董事长 黄泽帆
超凡妈妈项目共同发起人(原聚成股份董事长)陈其仁对超凡妈妈这一项目的使命和未来愿景进行了生动的介绍。他表示,超凡妈妈项目是“爱(ai)+AI”的天赋教育,融合了深情母爱与前沿人工智能技术,让每个孩子都能在爱与科技的双重滋养下,释放他们的天赋,成就非凡的未来。

超凡妈妈项目共同发起人(原聚成股份董事长)陈其仁
璀璨启幕全新华章
随着发布会气氛的升温,中国关心下一代健康体育基金会副主任兼秘书长曾芝冰,北京大学生命科学学院北生英才主任曹可盈,清华大学计算机博士张博,蓝笔科技董事长黄泽帆,超凡妈妈项目共同发起人(原聚成股份董事长)陈其仁,超凡妈妈项目共同发起人、蓝笔科技联合创始人王超然共同登台,宣布超凡妈妈赋能计划正式启动!

启动仪式合影
随后,超凡妈妈项目共同发起人、百万粉丝育儿博主陈小璟作为妈妈团代表上台发言。她表示,作为一位母亲,希望能够在孩子们身上弥补自己成长过程中的缺憾,确保他们能够获得精准的学科规划和教育,这份初衷,更加坚定了她自己成为超凡妈妈,投身于超凡妈妈赋能计划的决心。

超凡妈妈项目共同发起人 陈小璟
行业圆桌交流会,探讨超凡可能性
一场主题为“超凡可能性”的圆桌论坛汇聚了多位重量级嘉宾,就超凡妈妈项目发展、异业合作空间和女性力量等话题进行了深入讨论,并分享了各自的观点和见解。
超凡妈妈共同创始人王超然深入分析了超凡妈妈项目的超凡可能性。他认为,超凡妈妈赋能计划既符合当今女性觉醒的时代潮流,又能通过人工智能技术赋能生涯规划师,给普通家庭提供高端化、定制化、真正因材施教的优质教育,是具有超凡可能性的商业项目。他表示,希望将超凡妈妈项目打造成异业合作赋能爆款IP,为合作企业提供核心价值,成为未来商业领域的独角兽。清华大学计算机博士张博认为,AI技术即将在中国教育体制改革中起到举足轻重的超凡作用。太子家居直营公司总经理帅博文希望与超凡妈妈项目合作,根据儿童的兴趣爱好,开发智能化的儿童桌,打造嵌入AI技术的儿童房,量身定制适宜儿童的家居环境。凯丽思医学美容集团执行董事易琛善提出,希望借助超凡妈妈计划,打造全息幸福的医美解决方案,从亲子关系、夫妻关系、父母关系给女性客户提供一站式解决方案。

圆桌交流会
发布会尾声,超凡妈妈项目共同发起人(原聚成股份董事长)陈其仁先生与宁波指尖教育科技有限公司董事长颜子锦、太子家居直营公司总经理帅博文、凯丽思医学美容集团执行董事易琛善、以及湖北宜都市兴华矿业有限公司董事长胡学强进行了正式的签约仪式,这标志着超凡妈妈赋能计划正式启动,为女性创业注入新活力。

签约环节
超凡妈妈赋能计划,作为公益教育事业,不仅是对妈妈们潜力的深入挖掘和全面赋能,更是对未来一代的深情投资与关怀。
相关文章:

蓝笔科技 | 超凡妈妈赋能计划-【北大生涯规划师特别企划】
12月27日,“超凡妈妈赋能计划-北大生涯规划师特别企划”在广州正式启动,据了解,本次超凡妈妈赋能计划是由广州蓝笔科技信息有限公司牵头发起并主办,中国关心下一代健康体育基金会作为公益支持单位,北京大学作为项目技术…...
【电路笔记 TMS320C6***DSP】C6748 EDMA3配置笔记 寄存器配置+影子通道寄存器+配置示例
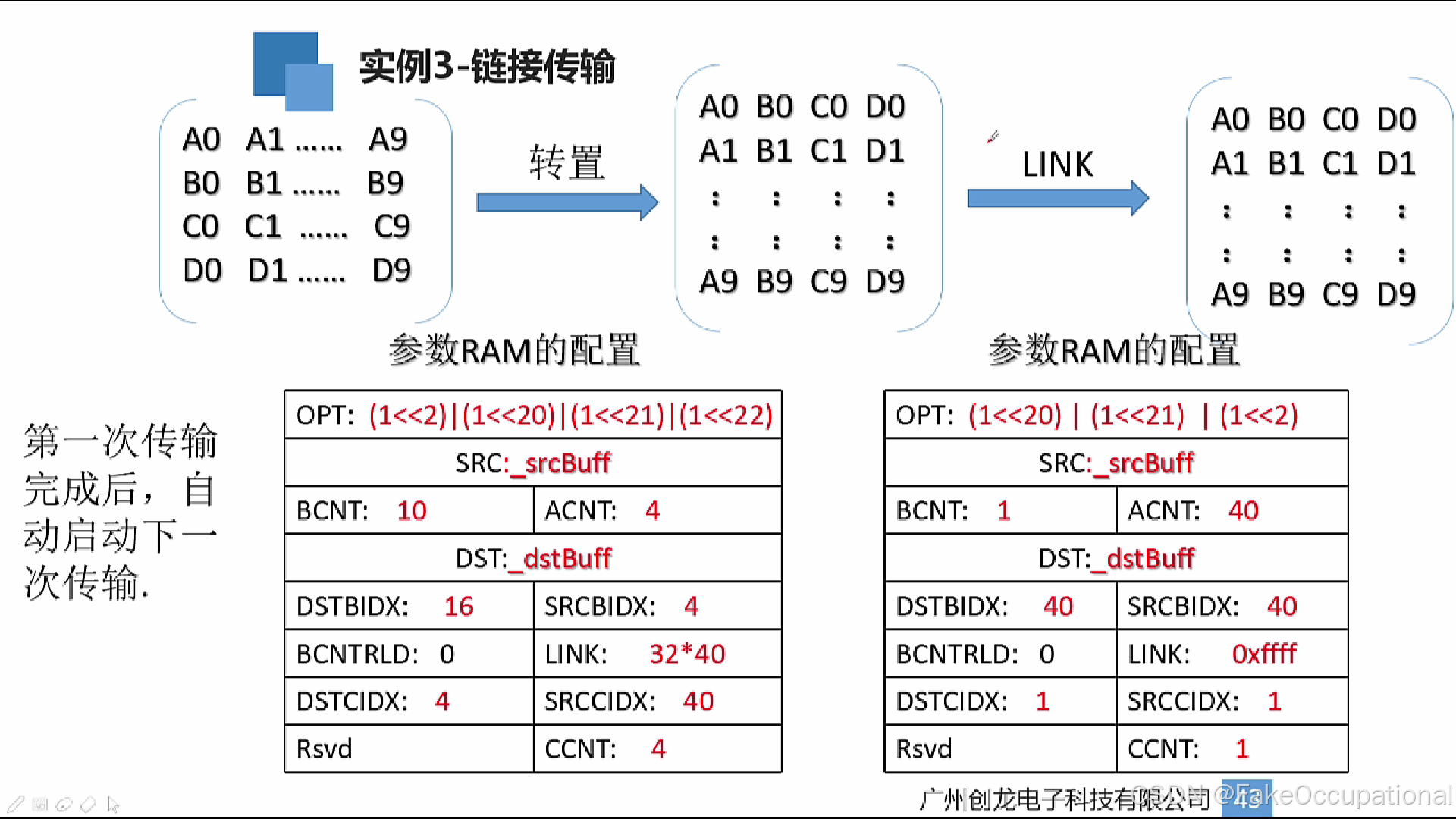
目录 参照资料内存映射寄存器分类影子通道寄存器传输中断PaRAM参数SRC、DSTA_B_CNT、CCNTSRC_DST_BIDXSRC_DST_CIDXOPTopt示例 链接传输LINK_BCNTRLD (LinkAddress/BCountReloadParameter)示例代码示例配置:块传输示例配置:矩阵转置示例配置:…...

2025新春烟花代码(二)HTML5实现孔明灯和烟花效果
效果展示 源代码 <!DOCTYPE html> <html lang"en"> <script>var _hmt _hmt || [];(function () {var hm document.createElement("script");hm.src "https://hm.baidu.com/hm.js?45f95f1bfde85c7777c3d1157e8c2d34";var …...

apollo内置eureka dashboard授权登录
要确保访问Eureka Server时要求输入账户和密码,需要确保以下几点: 确保 eurekaSecurityEnabled 配置为 true:这个配置项控制是否启用Eureka的安全认证。如果它被设置为 false,即使配置了用户名和密码,也不会启用安全认…...

后台管理系统全屏功能实现
后台管理系统中有一个比较常见的功能就是全屏显示,以方便用最大的屏幕查看系统,特别是在小屏模式下。 对于 screenfull 而言,浏览器本身已经提供了对用的 API,点击这里即可查看,这个 API 中,主要提供了两个…...

风电叶片市场竞争激烈:开启绿色能源新篇章的巨大潜力
一、引言 面对全球气候变化的严峻挑战,可再生能源的开发与利用已成为各国共识。风电,作为技术最成熟、最具规模化开发条件的可再生能源之一,正以前所未有的速度发展。而风电叶片,作为风电机组的核心部件,其技术创新与…...

【Unity3D日常开发】Unity3D中适用WEBGL打开Window文件对话框打开/上传文件
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享QQ群:398291828小红书小破站 大家好,我是佛系工程师☆恬静的小魔龙☆,不定时更新Unity开发技巧,觉得有用记得一键三连哦。 一、前言 Unity3D发布的WEBGL程序是不支持直接的I/O操…...

C# 或 .NetCore 如何使用 NPOI 导出图片到 Excel 文件
今天在本文中,我们将尝试使用NPOI库将图像插入到 Excel 文件的特定位置。请将以下逻辑添加到您的写作方法中,在 Excel 文件中添加图像(JPEG、PNG),我已经有一个示例 jpeg 文件 - Read-write-excel-npoi.jpg ,我们将尝试…...

Lambda expressions in C++ (C++ 中的 lambda 表达式)
Lambda expressions in C {C 中的 lambda 表达式} 1. Parts of a lambda expression (Lambda 表达式的各个部分)1.2. Parameter list (Optional) References lambda /ˈlm.də/:the 11th letter of the Greek alphabet (希腊语字母表的第 11 个字母)https://learn.m…...

【Rust自学】11.4. 用should_panic检查恐慌
喜欢的话别忘了点赞、收藏加关注哦,对接下来的教程有兴趣的可以关注专栏。谢谢喵!(・ω・) 11.4.1. 验证错误处理的情况 测试函数出了验证代码的返回值是否正确,还需要验证代码是否如预期的去处理了发生错误的情况。比…...

高斯函数Gaussian绘制matlab
高斯 约翰卡尔弗里德里希高斯,(德语:Johann Carl Friedrich Gau,英语:Gauss,拉丁语:Carolus Fridericus Gauss)1777年4月30日–1855年2月23日,德国著名数学家、物理学家…...

获取客户端真实IP地址
当处理来自客户端的请求时,尤其是在存在代理服务器的情况下,可能需要考虑多种HTTP请求头,以尽可能准确地获取用户的真实IP地址。以下是考虑了X-Forwarded-For、Proxy-Client-IP、WL-Proxy-Client-IP、HTTP_CLIENT_IP、HTTP_X_FORWARDED_FOR的…...
)
Kotlin学习(一)
1. Kotlin 作用域函数 如果同学们已经在项目中用过 Kotlin 语言,那么一定见过 let 函数!因为每当 Kotlin 检测到某个对象可能为空时,会自动帮我们修改为用 let 函数实现:user.name?.let{ textView.text it }。这里的 let 函数就…...

鸿蒙UI开发——日历选择器
1、概 述 在项目开发中,我们时常会用到日历选择器,效果如下: ArkUI已经为我们提供了组件,我们可以直接使用,下面针对日历组件做简单介绍。 2、CalendarPickerDialog 接口定义如下: // 定义日历选择器弹…...

2025-1-9 QT 使用 QXlsx库 读取 .xlsx 文件 —— 导入 QXlsx库以及读取 .xlsx 的源码 实践出真知,你我共勉
文章目录 1. 导入QXlsx库2. 使用 QXlsx库 读取 .xlsx 文件小结 网上有很多教程,但太费劲了,这里有个非常简便的好方法,分享给大家。 1. 导入QXlsx库 转载链接 :https://github.com/QtExcel/QXlsx/blob/master/HowToSetProject.md…...

React中createRoot函数原理解读——Element对象与Fiber对象、FiberRootNode与HostRootNode
【2024最新版】React18 核心源码分析教程(全61集) Element对象与Fiber对象 在 React 中,Element 对象 和 Fiber 对象 是核心概念,用于实现 React 的高效渲染和更新机制。以下是它们的详细解读: 1. Element 对象 定…...

利用Python实现Union-Find算法
Union-Find(又称 并查集)是一种高效解决 动态连通性问题 的算法。它主要提供两种操作: Union(x, y):将元素 x 和 y 连接。Find(x):找到元素 x 所属的集合的标识符(通常是集合的根节点)。 常用…...

【LeetCode: 912. 排序数组 + 归并排序】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...

AI时代来了,我们不再需要IDE了
大家好,我是编程乐趣。 最近在思考一个问题,那就是AI这么强大。 未来有没有可能,我们就不需要不需要开发工具了,只需一个浏览器就可以开发软件了。 一、AI带来的变化 1、代码生成与补全 AI工具如GitHub Copilot等能够根据代码…...

PL/SQL语言的网络编程
PL/SQL语言的网络编程 引言 在信息化迅速发展的今天,网络编程作为现代软件开发的重要组成部分,受到了广泛关注。而在数据库管理系统中,Oracle 提供了 PL/SQL(Procedural Language/Structured Query Language)&#x…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
