AI刷题-最大矩形面积问题、小M的数组变换
目录
一、最大矩形面积问题
问题描述
输入格式
输出格式
输入样例
输出样例
数据范围
解题思路:
问题理解
数据结构选择
算法步骤
最终代码:
运行结果:
二、小M的数组变换
问题描述
测试样例
解题思路:
问题理解
关键点
解题思路
算法步骤
最终代码:
运行结果:
一、最大矩形面积问题
问题描述
对于一个有 N 个元素的数组,包含如下的元素 h1, h2, ..., hn,对于 k 个相邻的元素,我们定义它的最大面积如下:
R(k)=k∗min(h[i],h[i+1],....,h[i+k−1])R(k)=k∗min(h[i],h[i+1],....,h[i+k−1])
求 R(k) 的最大值
输入格式
总共有两行,第一行是数组长度 N,第二个是空格分割的所有数组的内容
输出格式
输出 R(k) 的最大值
输入样例
5
1 2 3 4 5
输出样例
9
数据范围
- 1 <= N <= 10^5
- 1 <= h[i] <= 10^6
解题思路:
问题理解
我们需要在一个数组中找到一个长度为 k 的子数组,使得这个子数组的最小值乘以 k 的值最大。换句话说,我们需要最大化 R(k) = k * min(h[i], h[i + 1], ..., h[i + k - 1])。
数据结构选择
由于数组的长度 N 最大可以达到 10^5,我们需要一个高效的算法来解决这个问题。我们可以考虑使用滑动窗口(Sliding Window)技术来遍历所有可能的子数组,并使用一个数据结构来快速找到窗口内的最小值。
算法步骤
- 初始化:定义一个变量
max_area来存储当前找到的最大面积。 - 滑动窗口:使用两个指针
left和right来表示当前窗口的左右边界。 - 计算最小值:在每次移动窗口时,计算当前窗口内的最小值。
- 更新最大面积:计算当前窗口的最小值乘以窗口长度
k,并与max_area比较,更新max_area。 - 移动窗口:将窗口向右滑动一个位置,继续上述步骤,直到遍历完整个数组。
最终代码:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;int solution(int n, std::vector<int> A) {int max_area = 0;// 遍历所有可能的 kfor (int k = 1; k <= n; ++k) {// 遍历所有可能的起始位置 ifor (int i = 0; i <= n - k; ++i) {// 计算当前 k 个元素的最小值int min_height = *min_element(A.begin() + i, A.begin() + i + k);// 计算当前的面积int area = k * min_height;// 更新最大面积max_area = max(max_area, area);}}return max_area;
}int main() {// 添加测试用例std::vector<int> A_case1 = std::vector<int>{1, 2, 3, 4, 5};std::cout << (solution(5, A_case1) == 9) << std::endl;return 0;
}运行结果:

二、小M的数组变换
问题描述
小M拿到一个数组,她可以进行多次操作,每次操作可以选择两个元素 aiai 和 ajaj,并选择 aiai 的一个因子 xx,然后将 aiai 变为 ai/xai/x,并将 ajaj 变为 aj×xaj×x。她的目标是通过有限次操作,使得数组中的每个元素最多只包含一种素因子。
素因子的定义是:若 xx 能被素数 pp 整除,那么 pp 是 xx 的一个素因子。例如,1212 的素因子有 22 和 33。
你的任务是判断是否有可能通过有限次操作,使数组中的每个元素最多只包含一种素因子。如果可以,输出 "Yes",否则输出 "No"。
测试样例
样例1:
输入:
n = 4 ,a = [1, 2, 3, 4]
输出:'Yes'
样例2:
输入:
n = 2 ,a = [10, 12]
输出:'No'
样例3:
输入:
n = 3 ,a = [6, 9, 15]
输出:'Yes'
解题思路:
问题理解
我们需要判断是否可以通过有限次操作,使得数组中的每个元素最多只包含一种素因子。每次操作可以选择两个元素 ai 和 aj,并选择 ai 的一个因子 x,然后将 ai 变为 ai/x,并将 aj 变为 aj×x。
关键点
- 素因子分解:每个数都可以分解为若干个素因子的乘积。例如,12 可以分解为 2 * 2 * 3。
- 操作的本质:通过操作,我们可以将一个数的素因子转移到另一个数上。
- 目标:最终每个数只包含一种素因子。
解题思路
- 素因子集合:首先,我们需要找出每个数的所有素因子。
- 素因子图:将每个数的素因子看作图中的节点,如果两个数共享同一个素因子,则在它们之间建立一条边。
- 连通性:如果这个图是连通的,那么我们可以通过操作将所有素因子集中到某些数上,使得每个数只包含一种素因子。
- 判断连通性:可以使用并查集(Union-Find)来判断图的连通性。
算法步骤
- 素因子分解:对每个数进行素因子分解,记录每个数的素因子集合。
- 构建并查集:将每个素因子作为一个节点,如果两个数共享同一个素因子,则将它们对应的素因子节点进行合并。
- 判断连通性:最终判断并查集中是否只有一个连通分量。
最终代码:
#include <bits/stdc++.h>
using namespace std;
string solution(int n,vector<int>& a)
{set<int> st;for (auto&& ai : a){int sai = ceil(sqrt(ai));for(int j=2;j<=ai && j<=sai;j++){while(ai%j == 0){ai /= j;st.insert(j);}}if(ai != 1) st.insert(ai);}return st.size()<=a.size() ? "Yes" : "No";
}int main() {vector<int> a1 = {1, 2, 3, 4};vector<int> a2 = {10, 12};vector<int> a3 = {6, 9, 15};cout << (solution(4, a1) == "Yes") << endl;cout << (solution(2, a2) == "No") << endl;cout << (solution(3, a3) == "Yes") << endl;return 0;
}运行结果:

相关文章:

AI刷题-最大矩形面积问题、小M的数组变换
目录 一、最大矩形面积问题 问题描述 输入格式 输出格式 输入样例 输出样例 数据范围 解题思路: 问题理解 数据结构选择 算法步骤 最终代码: 运行结果: 二、小M的数组变换 问题描述 测试样例 解题思路: 问题…...

Redis集群部署详解:主从复制、Sentinel哨兵模式与Cluster集群的工作原理与配置
集群部署形式 1、主从复制1.1 工作机制1.2 配置实现1.3 优缺点1.4 部署形式1.5 主从复制优化 2、Sentinel 哨兵模式2.1 工作机制2.2 配置实现2.3 优缺点2.4 哨兵机制选举流程2.5 脑裂问题解决方案 3、Redis Cluster3.1 工作机制3.2 配置实现3.3 优缺点3.4 故障转移3.5 哈希槽为…...
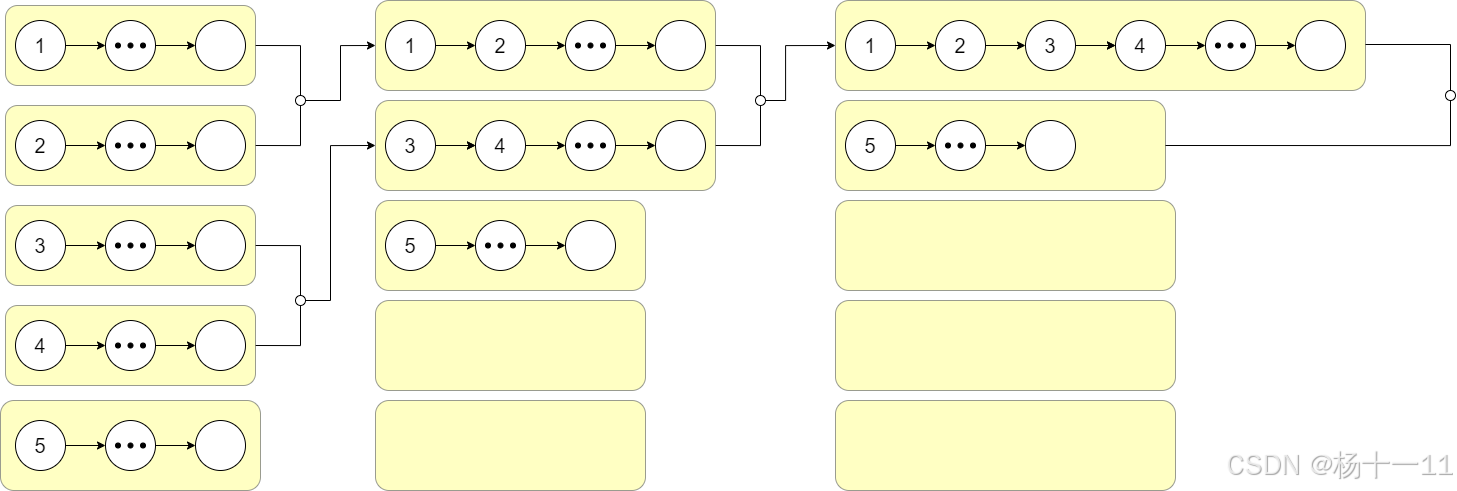
LeetCode热题100(三十四) —— 23.合并K个升序链表
LeetCode热题100(三十四) —— 23.合并K个升序链表 题目描述代码实现思路一:选择排序(199ms)思路二:归并排序(2ms) 思路解析 你好,我是杨十一,一名热爱健身的程序员在Coding的征程中,不断探索与…...

kalilinux - 目录扫描之dirsearch
情景导入 先简单介绍一下dirsearch有啥用。 假如你现在访问一个网站,例如https://www.example.com/ 它是一个电商平台或者其他功能性质的平台。 站在开发者的角度上思考,我们只指导https://www.example.com/ 但不知道它下面有什么文件,文…...

浅谈云计算04 | 云基础设施机制
探秘云基础设施机制:云计算的基石 一、云基础设施 —— 云计算的根基二、核心机制之网络:连接云的桥梁(一)虚拟网络边界ÿ…...

文件上传 分片上传
分片上传则是将一个大文件分割成多个小块分别上传,最后再由服务器合并成完整的文件。这种做法的好处是可以并行处理多个小文件,提高上传效率;同时,如果某一部分上传失败,只需要重传这一部分,不影响其他部分…...

【0391】Postgres内核 checkpointer process ① 启动初始化
相关文章: 【0108】checkpointer运行原理(概念篇)(1) 【0278】checkpointer 共享内存(CheckpointerShmem)初始化(3) 文章目录 1. 启动 checkpointer process1.1 初始化 checkpointer PID1.2 注册 signal1.3 初始化 last checkpoint time2. 确认 config 的 shared memo…...

链路追踪SkyWalking
链路追踪 链路追踪作用链路追踪的关键概念链路追踪的工作原理常用链路追踪工具链路追踪的实现步骤链路追踪的典型场景 SkyWalkingSkyWalking 的主要功能SkyWalking 的架构安装 SkyWalking从 SkyWalking 的官方 GitHub 仓库 下载最新版本。配置后端存储SkyWalking使用࿰…...

Uniapp判断设备是安卓还是 iOS,并调用不同的方法
在 UniApp 中,可以通过 uni.getSystemInfoSync() 方法来获取设备信息,然后根据系统类型判断当前设备是安卓还是 iOS,并调用不同的方法。 示例代码 export default {onLoad() {this.checkPlatform();},methods: {checkPlatform() {// 获取系…...

计算机网络 (42)远程终端协议TELNET
前言 Telnet(Telecommunication Network Protocol)是一种网络协议,属于TCP/IP协议族,主要用于提供远程登录服务。 一、概述 Telnet协议是一种远程终端协议,它允许用户通过终端仿真器连接到远程主机,并在远程…...

rtthread学习笔记系列-- 23 环形缓冲块 ringblock
文章目录 23 环形缓冲块 ringblock23.1 初始化23.2 PUT & GET 块23.3 块释放23.4 rt_rbb_blk_queue_get23.5 rt_rbb_blk_alloc https://github.com/wdfk-prog/RT-Thread-Study 23 环形缓冲块 ringblock 环形块状缓冲区简称为:rbb。与传统的环形缓冲区不同的是&…...

HunyuanVideo 文生视频模型实践
HunyuanVideo 文生视频模型实践 flyfish 运行 HunyuanVideo 模型使用文本生成视频的推荐配置(batch size 1): 模型分辨率(height/width/frame)峰值显存HunyuanVideo720px1280px129f60GHunyuanVideo544px960px129f45G 本项目适用于使用 N…...
)
Qt——QTableWidget 限制单元格输入范围的方法(正则表达式输入校验法、自定义代理类MyItemDelegrate)
【系列专栏】:博主结合工作实践输出的,解决实际问题的专栏,朋友们看过来! 《项目案例分享》 《极客DIY开源分享》 《嵌入式通用开发实战》 《C++语言开发基础总结》 《从0到1学习嵌入式Linux开发》...

深度学习论文: CAS-ViT: Convolutional Additive Self-attention Vision Transformers
深度学习论文: CAS-ViT: Convolutional Additive Self-attention Vision Transformers for Efficient Mobile Applications CAS-ViT: Convolutional Additive Self-attention Vision Transformers for Efficient Mobile Applications PDF:https://arxiv.org/pdf/2408.03703 PyT…...

PyCharm文档管理
背景:使用PyCharmgit做文档管理 需求:需要PyCharm自动识别docx/xslx/vsdx等文件类型,并在PyCharm内点击文档时唤起系统内关联应用(如word、excel、visio) 设置步骤: 1、file -》 settings -》file types 2、在Files opened i…...

QNAP 上常用的几款软件
当我们谈到 NAS(Network Attached Storage)时,QNAP 凭借多年的产品迭代、稳定的硬件性能和不断丰富的软件生态,已成为很多家庭及中小型企业的首选。除了存储本身,QNAP 提供的各种官方软件和应用,也为用户带…...

LabVIEW智能水肥一体灌溉控制系统
本文详细介绍了一种基于LabVIEW的智能水肥一体灌溉控制系统的设计与实现。该系统采用模糊控制策略,能够自动调节土壤湿度和肥液浓度,满足不同作物在不同生长阶段的需求,有效提高水肥利用效率,对现代精准农业具有重要的实践和推广价…...

提问:玩游戏输入法总弹出来咋回事哎
玩游戏时输入法总弹出来的问题,通常与电脑的输入法设置、操作系统配置以及游戏程序的兼容性有关。以下是一些常见的解决方法: 一、修改输入法快捷键 禁用不必要的输入法: 在系统的语言设置中,暂时禁用非活动的输入法,…...

链家房价数据爬虫和机器学习数据可视化预测
完整源码项目包获取→点击文章末尾名片!...

【微服务】面试题 5、分布式系统理论:CAP 与 BASE 详解
分布式系统理论:CAP 与 BASE 详解 一、CAP 定理 背景与定义:1998 年由加州大学科学家埃里克布鲁尔提出,分布式系统存在一致性(Consistency)、可用性(Availability)、分区容错性(Part…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...
