欧几里得算法求最小公倍数和最大公约数
一.最大公约数
gcd(a,b)=gcd(b,a%b) 递归式,当且仅当b=0,易得0和a的公约数为a.(可作为递归的出口)
证明:

int gcd(int a, int b)
{if (b == 0) return a;else return gcd(b, a % b);
}二.最小公倍数
给定整数a b,求a b的最小公倍数
有图可知
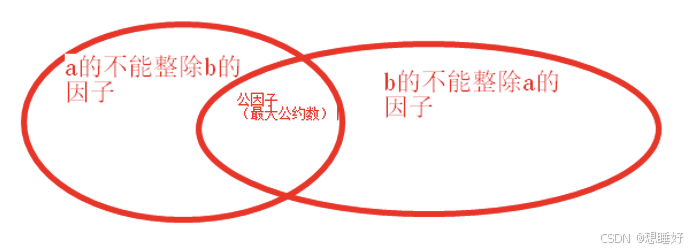
a和b 的最小公倍数等于a*b/gcd(a,b),两个数相乘等价于a,b所有因子相乘,但中间共同部分多乘了一次,多乘的部分为a和b的最大公约数
int gcd(int a, int b)
{if (b == 0) return a;else return gcd(b, a % b);
}
int main()
{int a = 6, b = 4;//最大公约数cout << gcd(a,b)<<endl;//最小公倍数cout << a * b / gcd(a, b);
}
相关文章:

欧几里得算法求最小公倍数和最大公约数
一.最大公约数 gcd(a,b)gcd(b,a%b) 递归式,当且仅当b0,易得0和a的公约数为a.(可作为递归的出口) 证明: int gcd(int a, int b) {if (b 0) return a;else return gcd(b, a % b); } 二.最小公倍数 给定整数a b,求a b的最小公倍数 有图可知…...

Selenium配合Cookies实现网页免登录
文章目录 前言1 方案一:使用Chrome用户数据目录2 方案二:手动获取并保存Cookies,后续使用保存的Cookies3 注意事项 前言 在进行使用Selenium进行爬虫、网页自动化操作时,登录往往是一个必须解决的问题,但是Selenium每次…...
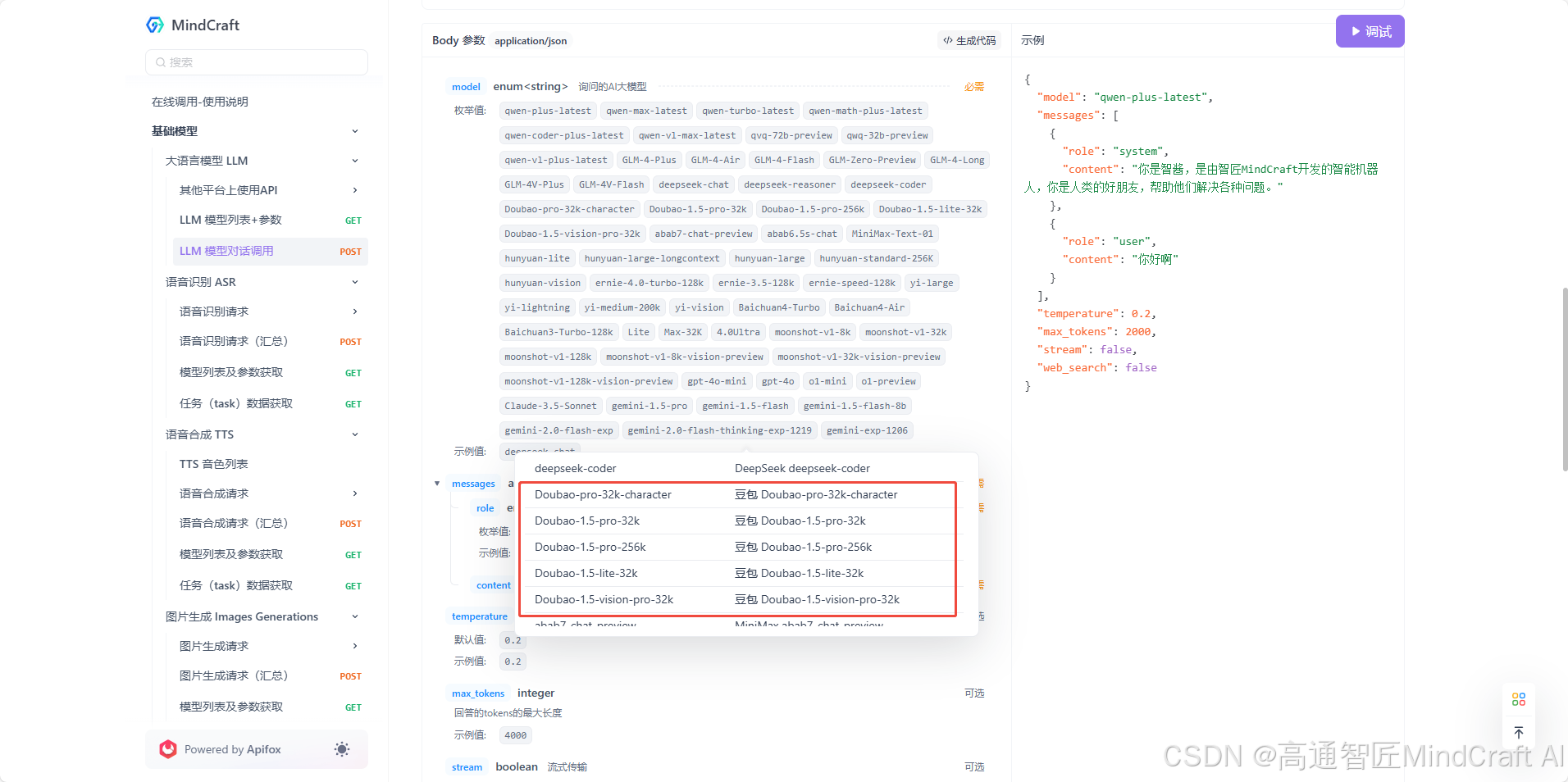
DeepSeek R1模型解读与使用
字节在春节前发布了doubao-1.5,它的官方介绍竟然是这样的: 这次发布了四个型号,doubao-1.5-pro-32k, doubao-1.5-pro-256k, doubao-1.5-lite-32k, doubao-1.5-vision-pro-32k,价格全部与上一个版本doubao模型一致,加量…...

Windows电脑不小心点击了关机,关机过程中如何阻止
如果电脑正在关机的过程中,想要阻止关机,可以尝试以下方法: 如果关机过程较慢,可以按下键盘组合键 Win R 打开运行窗口。输入 shutdown -a 后按回车键,这将中断关机操作(适用于 Windows 系统)…...
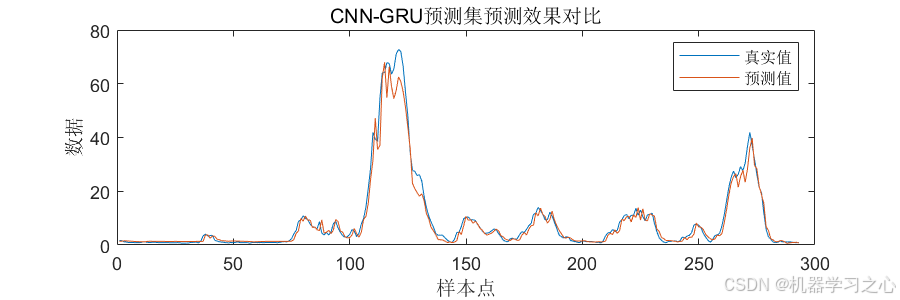
CNN-GRU卷积门控循环单元时间序列预测(Matlab完整源码和数据)
CNN-GRU卷积门控循环单元时间序列预测(Matlab完整源码和数据) 目录 CNN-GRU卷积门控循环单元时间序列预测(Matlab完整源码和数据)预测效果基本介绍CNN-GRU卷积门控循环单元时间序列预测一、引言1.1、研究背景与意义1.2、研究现状1…...

【吉林乡镇界】面图层shp格式arcgis数据乡镇名称和编码wgs84无偏移内容测评
标题中的“吉林省乡镇界面图层shp格式arcgis数据乡镇名称和编码wgs84无偏移”揭示了这是一个地理信息系统(GIS)相关的数据集,主要用于描绘吉林省的乡镇边界。这个数据集包含了一系列的文件,它们是ArcGIS软件能够识别和处理的Shape…...

fpga学习入门 串口rs232回环
奇偶检验位这里是省略了 做好回环后可以使用上位机做回环测试,top文件写的方式就是将rx(fpga端)接受到的模块(pc端)tx发送出去,这两个端口用杜邦线连接,同理模块的rx连接fpga的tx,…...

智启未来,AI筑梦科技新星”------华清远见成都中心2025冬令营圆满结束
2025年1月11日-16日,华清远见成都中心为期6天的“智启未来,AI筑梦科技新星”2025冬令营活动圆满结束。此次活动吸引了众多对人工智能和无人驾驶技术充满热情的学生参与,共同开启了一段点燃科技梦想的精彩旅程。 报道接待 以AI无人驾驶小车为核…...
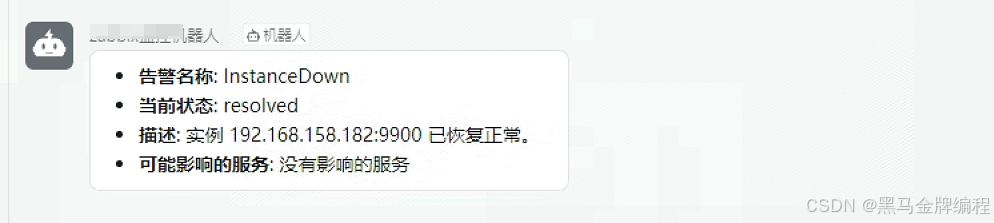
接上篇基于Alertmanager 配置钉钉告警
Alertmanager 是一个用于处理和管理 Prometheus 警报的开源工具。它负责接收来自 Prometheus 服务器的警报,进行去重、分组、静默、抑制等操作,并通过电子邮件、PagerDuty、Slack 等多种渠道发送通知。 主要功能 去重:合并相同或相似的警报&a…...

DDD - 如何设计支持快速交付的DDD技术中台
文章目录 Pre概述打造快速交付团队烟囱式的开发团队(BAD)大前端技术中台(GOOD) 技术中台的特征简单易用的技术中台建设总结 Pre DDD - 软件退化原因及案例分析 DDD - 如何运用 DDD 进行软件设计 DDD - 如何运用 DDD 进行数据库设计 DDD - 服务、实体与值对象的两种设计思路…...

JAVA与数据结构-线性表
目录 一.线性表的概念 二.线性表的关系及分类 三.数组与顺序表 四.链表 1.静态链表(链表的的数组底层实现) 2.循环链表 3.双向链表 五.栈 1.栈的概念 2.栈的底层实现 3.共享空间栈 4.逆波兰表达式(后缀表达式) 5.栈与递归 六.…...

C++|开源日志库log4cpp和glog
文章目录 log4cpp 和 glog对比1. **功能对比**2. **易用性和配置**3. **性能**4. **线程安全**5. **日志输出**6. **功能扩展**7. **适用场景**8. **总结** 其它开源C日志库1. **spdlog**2. **easylogging**3. **Boost.Log**4. **loguru**5. **Poco Logging**6. **Qt Logging (…...

React Context 实现全局组件注册
来源于GPT4o:https://ai.openaicloud.cn/?inVitecodeEJSTWFZMQE 第一步:创建全局组件上下文 (GlobalComponentProvider) 我们将创建一个 React Context 和 Provider,用于存储和提供全局组件。 // src/context/GlobalComponentProvider.tsx…...

基于AutoDL云计算平台+LLaMA-Factory训练平台微调本地大模型
1. 注册与认证 访问AutoDL官网:前往 AutoDL官网。 注册账号:完成注册流程。 实名认证:按照要求完成实名认证,以确保账号的合规性。 2. 选择GPU资源 进入算力市场:在官网首页点击“算力市场”菜单。 挑选GPU&#x…...

strdup 函数
strdup 函数是 C 标准库中的一个函数,用于复制一个字符串。它的全称是 "string duplicate"。这个函数在 <string.h> 头文件中声明。strdup 函数会分配足够的内存来存储源字符串的副本,并将源字符串的内容复制到新分配的内存中。然后返回…...

2.9/Q2,Charls最新文章解读!
文章题目:The causal effect of Internet use on rural middle-aged and older adults depression: A propensity score matching analysis DOI:10.1177/20552076241310041 中文标题:互联网使用对农村中老年人抑郁症的因果影响:…...

【未完成】springboot项目实现扫码登录相关逻辑
准备工作 配置redis 引入redis依赖 <dependencies><!-- Spring Data Redis 依赖 --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId></dependency><…...

html、js、css实现爱心效果
好的!我们可以进一步美化这个爱心效果,增加更多动态和视觉吸引力。以下是改进后的代码,包括以下功能: 1. 背景渐变:添加动态背景渐变效果。 2. 爱心阴影:为爱心添加阴影,使其更具立体感。 3. 随…...

【前端】Hexo 建站指南
文章目录 前言生成站点本地测试部署云端参考 前言 更好的阅读体验:https://blog.dwj601.cn/FrontEnd/Hexo/build-your-own-website-with-hexo/ 笔记记多了,想要分享给同学们一起交流进步,该怎么办?想要搭建一个属于自己的知识库…...

OpenStack基础架构
openstack是一套IaaS云的解决方案,是一个开源的云计算管理平台 每一台物理机上都会有一个nova服务器 虚拟化其实是在nova主机里启用的 COW技术: 这么来看,3个物理机上产生10个虚拟机,所以把服务分散到10个虚拟机上和分散到4个虚拟…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
