洛谷——P1004 方格取数
【题目描述】
设有 N×N 的方格图 (N≤9),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 0。如下图所示(见样例):
A
0 0 0 0 0 0 0 0
0 0 13 0 0 6 0 0
0 0 0 0 7 0 0 0
0 0 0 14 0 0 0 0
0 21 0 0 0 4 0 0
0 0 15 0 0 0 0 0
0 14 0 0 0 0 0 0
0 0 0 0 0 0 0 0
B
某人从图的左上角的 A 点出发,可以向下行走,也可以向右走,直到到达右下角的 B 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 0)。
此人从 A 点到 B 点共走两次,试找出 2 条这样的路径,使得取得的数之和为最大。
【输入】
输入的第一行为一个整数 N(表示 N×N 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 0 表示输入结束。
【输出】
只需输出一个整数,表示 22 条路径上取得的最大的和。
样例输入
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
样例输出
67
解题思路
这个题目首先可能会想到用动态二维 dp 解题,但是会出现一个问题这个不像搜索,走到之后就直接标记,然后后面是不会走到了,动态规划解题的特点是:如果要得到最小值或者,就不停的遍历并更新 dp 数组里面的值。但是这个题需要走两遍,而且走过的路上的数字要清空(注意这里并不是不能经过)。
用一个四维 dp 数组解决,四层循环查找一遍就可以得到答案。
代码如下:
#include<stdio.h>
int book[10][10];
int dp[10][10][10][10];//四维动态 dp数组
int max(int x,int y)//求较大值的函数
{if(x<y)return y;elsereturn x;
}
int main()
{int n,a,b,c,i,j,l,k;scanf("%d",&n);while(scanf("%d %d %d",&a,&b,&c)!=EOF){if(a==0&&b==0&&c==0)//一行单独的 0代表输入结束 break;book[a][b]=c;}for(i=1;i<=n;i++){for(j=1;j<=n;j++){for(l=1;l<=n;l++){for(k=1;k<=n;k++){dp[i][j][l][k]=book[i][j]+book[l][k]+max(max(dp[i][j-1][l][k-1],dp[i-1][j][l-1][k]),max(dp[i-1][j][l][k-1],dp[i][j-1][l-1][k]));if(i==l&&j==k)dp[i][j][l][k]-=book[i][j];}} }}printf("%d\n",dp[n][n][n][n]);return 0;
}
这个方法应该也是可行的:除了动态 dp 数组,除了存放方格中数的 book 数组,再设置一个 flag 数组(只能向下走或者向右走),它的下标代表每一列经过的行数,每更新一次 dp 数组里面的值,就把行数的下标存入对应的 flag 数组。
这样进行完第一遍查找后,找到了方格取数的最大值,并且标记了走过的路径,接下来把走过的路径上面的方格数归为 0,然后进行第二遍查找。
两遍查找的最大值相加就是要求的答案。
相关文章:

洛谷——P1004 方格取数
【题目描述】 设有 NN 的方格图 (N≤9),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 0。如下图所示(见样例): A 0 0 0 0 0 0 0 0 0 0 13 0 0 6 0 0 0 0 0 0 7 0 0 0 0 0 0 14 0 0…...

Linux删除软链接
不防大家试试 unlink 命令 首先我们先来创建一个文件 #mkdir test_chk #touch test_chk/test.txt #vim test_chk/test.txt (这一步随便在这个test.txt里写点东东即可) 下面我们来创建test_chk目录 的软链接 #ln-s test_chk test_chk_ln 软链接创建好了,我们来…...
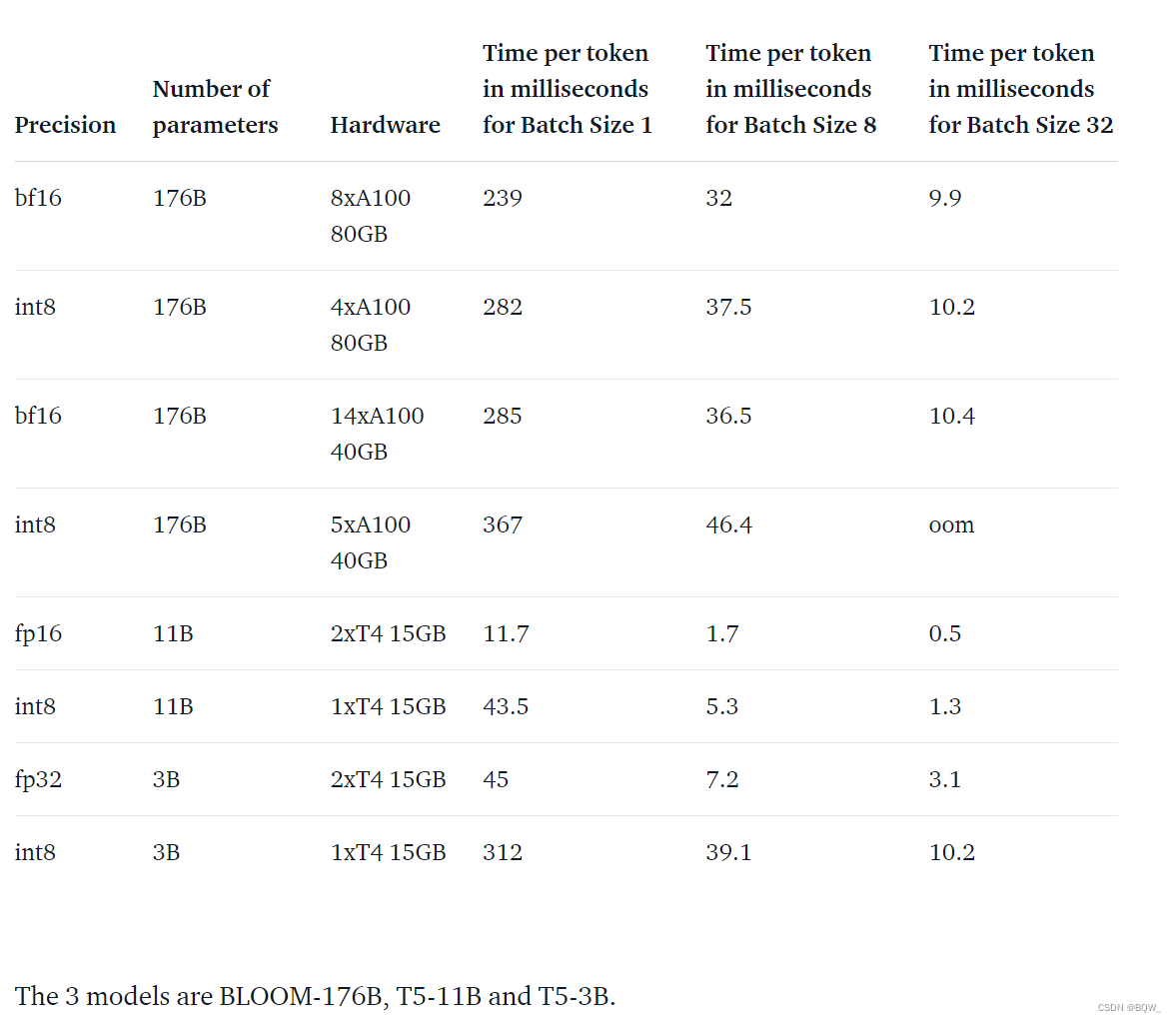
【自然语言处理】【大模型】用于大型Transformer的8-bit矩阵乘法介绍
用于大型Transformer的8-bit矩阵乘法介绍原文地址:A Gentle Introduction to 8-bit Matrix Multiplication for transformers at scale using transformers, accelerate and bitsandbytes 相关博客 【自然语言处理】【大模型】用于大型Transformer的8-bit矩阵乘法介…...
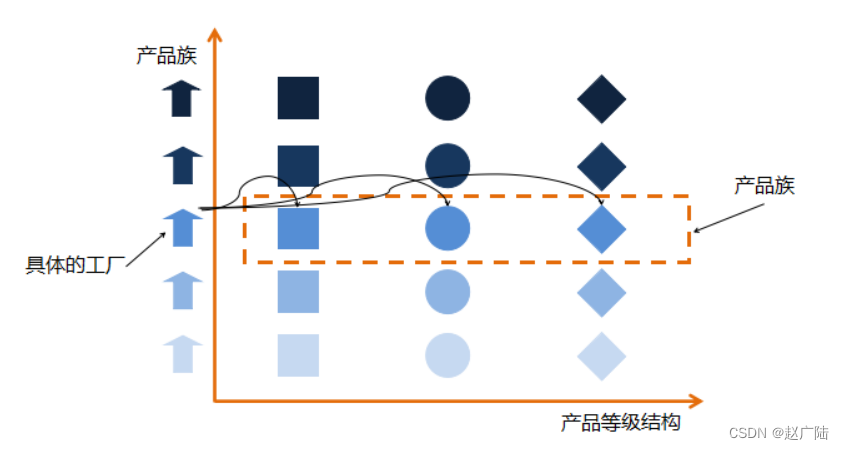
设计模式之工厂模式详解和应用
目录1 工厂模式的历史由来2.简单工厂模式2.1 简单工厂模式定义2.2 简单工厂模式案例2.3 简单工厂模式相关源码2.4 简单工厂模式优缺点3 工厂方法模式3.1 工厂方法模式定义3.2 工厂方法模式案例3.3 工厂方法模式源码3.4 工厂方法模式优缺点4 抽象工厂模式4.1 抽象工厂模式定义4.…...

ArcGIS中的附件功能
从ArcGIS10起,空间数据库增加了"附件"的功能,可灵活管理与要素相关的附加信息,可以是图像、PDF、文本文档或任意其他文件类型。例如,如果用某个要素表示建筑物,则可以使用附件来添加多张从不同角度拍摄的建筑物照片。 启动附件功能 要想使用附件功能,要素类必…...

epoll单台设备支持百万并发连接
一些概念: linux下一切接文件,文件描述符fd,文件I/O(包含socket,文本文件等),I/O多路复用,reactor模型,水平触发,边沿触发,多线程模型,阻塞和非阻塞…...

网络字节序
文章目录网络字节序网络字节序 内存中的多字节数据相对于内存地址有大端和小端之分, 磁盘文件中的多字节数据相对于文件中的偏移地址也有大端小端之分, 网络数据流同样有大端小端之分. 网络数据流的地址统一按大端处理 发送主机通常将发送缓冲区中的数据按内存地址从低到高的…...

03- SVC 支持向量机做人脸识别 (项目三)
数据集描述: sklearn的lfw_people函数在线下载55个外国人图片文件夹数据集来精确实现人脸识别并提取人脸特征向量数据集地址: sklearn.datasets.fetch_lfw_people — scikit-learn 1.2.1 documentationPCA降维: pca PCA(n_components0.9) 数据拆分: X_train, X_test, y_tra…...
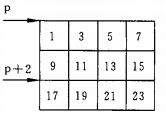
浅谈指向二维数组元素的指针变量
(1)指向数组元素的指针变量 例1.有一个3X4的二维数组,要求用指向元素的指针变量输出二维数组各元素的值. 编写程序 1 #include <stdio.h>2 int main()3 {4 int a[3][4] { 1,3,5,7,9,11,13,15,17,19,21,23 };5 int *p;6 for (p a[0]; p < a[0] 12; p) …...

左右值引用和移动语义
文章首发公众号:iDoitnow 1. 左右值和左右值引用 什么是左值、右值呢?一种极不严谨的理解为:在赋值的时候,能够被放到等号左边的值为左值,放在右边的值为右值。例如: int sum(int x, int y){return x y;…...

一起学习用Verilog在FPGA上实现CNN----(七)全连接层设计
1 全连接层设计 1.1 Layer 进行线性计算的单元layer,原理图如图所示: 1.2 processingElement Layer中的线性计算单元processingElement,原理图如图所示: processingElement模块展开原理图,如图所示,包含…...
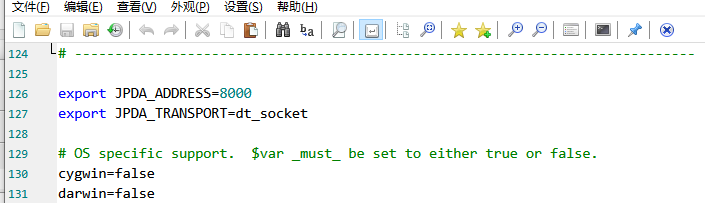
tomcat打debug断点调试
windows debug调试 jdk版本:1.8.0_181 tomcat版本:apache-tomcat-9.0.68.0 idea版本:2020.1 方法一 修改catalina.bat 在%CATALINA_HOME%\bin\catalina.bat中找到 set “JAVA_OPTS%JAVA_OPTS% -Djava.protocol.handler.pkgsorg.apache…...

如果持有互斥锁的线程没有解锁退出了,该如何处理?
文章目录如果持有互斥锁的线程没有解锁退出了,该如何处理?问题引入PTHREAD_MUTEX_ROBUST 和 pthread_mutex_consistent登场了结论:如果持有互斥锁的线程没有解锁退出了,该如何处理? 问题引入 看下面一段代码…...
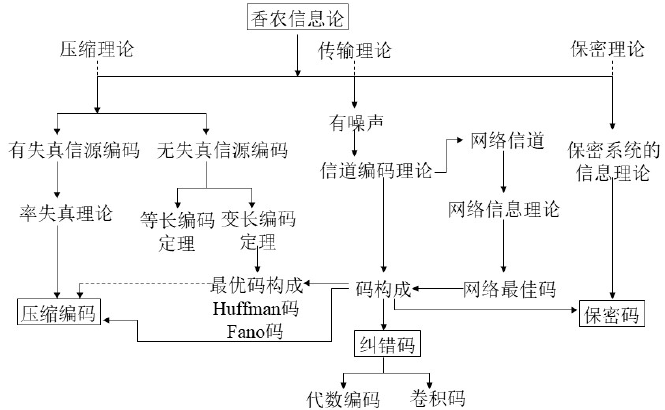
信息论绪论
本专栏针包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者关注公众号【AIShareLab】,回复 信息论 也可获取。 文章目…...

Buffer Status Reporting(BSR)
欢迎关注同名微信公众号“modem协议笔记”。 以一个实网中的异常场景开始,大概流程是有UL data要发送,UE触发BSR->no UL grant->SR->no UL grant->trigger RACH->RACH fail->RLF->RRC reestablishment:简单描述就是UE触…...

代码随想录LeetCode | 单调栈问题
前沿:撰写博客的目的是为了再刷时回顾和进一步完善,其次才是以教为学,所以如果有些博客写的较简陋,是为了保持进度不得已而为之,还请大家多多见谅。 预:看到题目后的思路和实现的代码。 见:参考…...

C++之可调用对象、bind绑定器和function包装器
可调用对象在C中,可以像函数一样调用的有:普通函数、类的静态成员函数、仿函数、lambda函数、类的非静态成员函数、可被转换为函数的类的对象,统称可调用对象或函数对象。可调用对象有类型,可以用指针存储它们的地址,可…...
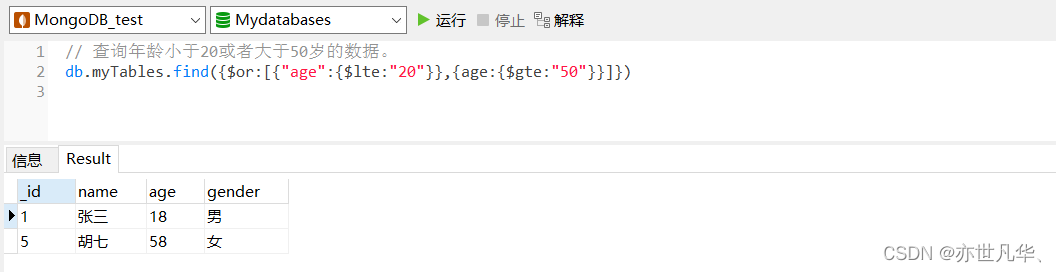
MongoDB--》文档查询的详细具体操作
目录 统计查询 分页列表查询 排序查询 正则的复杂条件查询 比较查询 包含查询 条件连接查询 统计查询 统计查询使用count()方法,其语法格式如下: db.collection.count(query,options) ParameterTypeDescriptionquerydocument查询选择条件optio…...
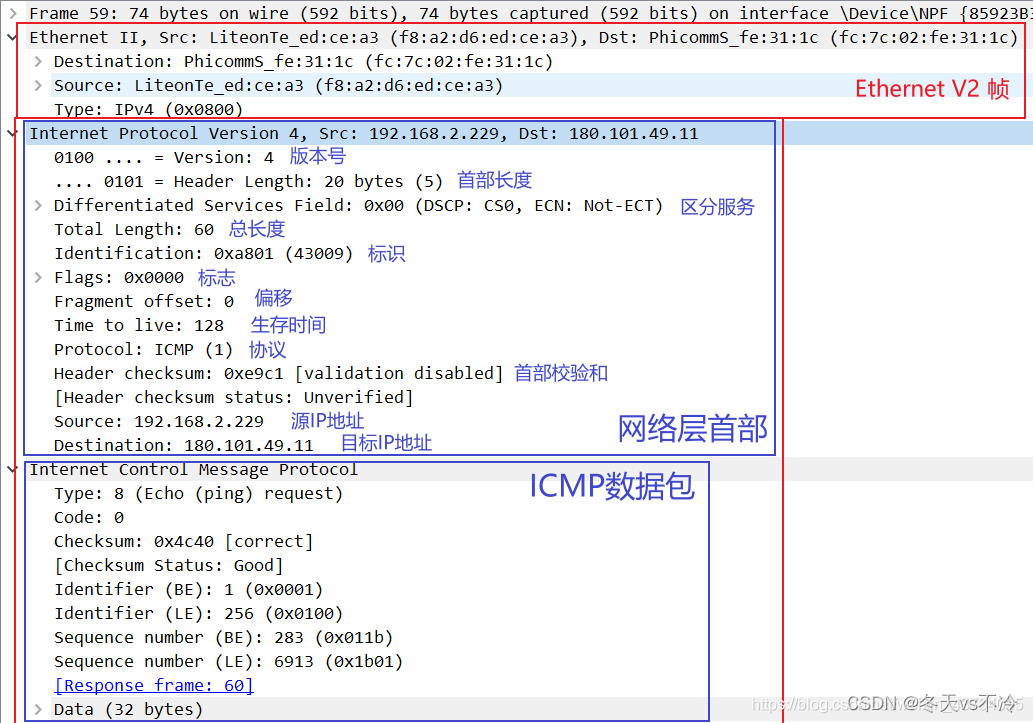
网络协议(六):网络层
网络协议系列文章 网络协议(一):基本概念、计算机之间的连接方式 网络协议(二):MAC地址、IP地址、子网掩码、子网和超网 网络协议(三):路由器原理及数据包传输过程 网络协议(四):网络分类、ISP、上网方式、公网私网、NAT 网络…...

热启动预示生态起航的Smart Finance,与深度赋能的SMART通证
2023年初加密市场的回暖,意味着各个赛道都将在新的一年里走向新的叙事。最近,我们看到GameFi赛道也在市场回暖的背景下,逐渐走出阴霾。从融资数据上看,1月获得融资的GameFi项目共12个,融资突破8000万美元,1…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...
EasyRTC音视频实时通话功能在WebRTC与智能硬件整合中的应用与优势
一、WebRTC与智能硬件整合趋势 随着物联网和实时通信需求的爆发式增长,WebRTC作为开源实时通信技术,为浏览器与移动应用提供免插件的音视频通信能力,在智能硬件领域的融合应用已成必然趋势。智能硬件不再局限于单一功能,对实时…...

C++ 类基础:封装、继承、多态与多线程模板实现
前言 C 是一门强大的面向对象编程语言,而类(Class)作为其核心特性之一,是理解和使用 C 的关键。本文将深入探讨 C 类的基本特性,包括封装、继承和多态,同时讨论类中的权限控制,并展示如何使用类…...
