Tree Compass( Codeforces Round 934 (Div. 2) )
Tree Compass( Codeforces Round 934 (Div. 2) )
You are given a tree with n n n vertices numbered 1 , 2 , … , n 1, 2, \ldots, n 1,2,…,n. Initially, all vertices are colored white.
You can perform the following two-step operation:
- Choose a vertex v v v ( 1 ≤ v ≤ n 1 \leq v \leq n 1≤v≤n) and a distance d d d ( 0 ≤ d ≤ n − 1 0 \leq d \leq n-1 0≤d≤n−1).
- For all vertices u u u ( 1 ≤ u ≤ n 1 \leq u \leq n 1≤u≤n) such that dist † ( u , v ) = d \text{dist}^\dagger(u,v)=d dist†(u,v)=d, color u u u black.
Construct a sequence of operations to color all the nodes in the tree black using the minimum possible number of operations. It can be proven that it is always possible to do so using at most n n n operations.
† ^\dagger † dist ( x , y ) \text{dist}(x, y) dist(x,y) denotes the number of edges on the (unique) simple path between vertices x x x and y y y on the tree.
Input
Each test contains multiple test cases. The first line contains a single integer t t t ( 1 ≤ t ≤ 200 1 \leq t \leq 200 1≤t≤200) — the number of test cases. The description of the test cases follows.
The first line of each test case contains a single integer n n n ( 1 ≤ n ≤ 2 ⋅ 1 0 3 1 \le n \le 2 \cdot 10^3 1≤n≤2⋅103) — the number of vertices of the tree.
The following n − 1 n - 1 n−1 lines of each test case describe the edges of the tree. The i i i-th of these lines contains two integers u i u_i ui and v i v_i vi ( 1 ≤ u i , v i ≤ n 1 \le u_i, v_i \le n 1≤ui,vi≤n, u i ≠ v i u_i \neq v_i ui=vi), the indices of the vertices connected by the i i i-th edge.
It is guaranteed that the given edges form a tree.
It is guaranteed that the sum of n n n over all test cases does not exceed 2 ⋅ 1 0 3 2 \cdot 10^3 2⋅103.
Output
For each test case, first output a single integer o p op op ( 1 ≤ o p ≤ n ) (1 \le op \le n) (1≤op≤n), the minimum number of operations needed to color all vertices of the tree black.
Then, output o p op op lines, each containing 2 2 2 integers. The i i i-th line should contain the values of v v v and d d d chosen for the i i i-th operation ( 1 ≤ v ≤ n 1 \le v \le n 1≤v≤n, 0 ≤ d ≤ n − 1 0 \le d \le n - 1 0≤d≤n−1)
You must guarantee that at the end of o p op op operations, all vertices are colored black.
If there are multiple solutions, you may output any one of them.
Example
Input
4121 241 21 31 472 73 26 45 71 66 7
Output
1
1 0
2
1 1
2 1
2
1 1
2 1
3
6 1
7 1
2 1
Note
In the first test case, there is only one possible operation, and performing it gives us a valid answer.
In the second test case, the first operation colors vertex 2 2 2 black, and the second operation colors vertex 1 1 1 black. It can be shown that it is impossible to color both vertices black in one operation, so the minimum number of operations needed is 2 2 2. Another possible solution is to use the 2 2 2 operations: ( u , r ) = ( 1 , 0 ) (u, r) = (1, 0) (u,r)=(1,0) and ( u , r ) = ( 2 , 0 ) (u, r) = (2, 0) (u,r)=(2,0).
In the third test case, the first operation colors vertices 2 2 2, 3 3 3 and 4 4 4 black, and the second operation colors vertex 1 1 1 black. Again, it can be shown that it is impossible to color all vertices black in 1 1 1 operation, so the minimum number of operations needed is 2 2 2.
In the fourth test case, the first operation colors vertices 4 4 4, 1 1 1 and 7 7 7 black, the second operation colors vertices 2 2 2, 5 5 5 and 6 6 6 black while the third operation colors vertices 3 3 3 and 7 7 7 black. Notice that it is allowed to color vertex 7 7 7 black twice.
Thus, each node was marked at least once, with node 7 7 7 marked twice. It can be shown that it is impossible to color all vertices black in fewer than 3 3 3 moves.
题解进一步分析和拓展
这个问题的关键在于树的直径,即树中两个最远节点之间的路径长度。直径的长度和树的染色策略有很大关系。接下来我们详细分析如何利用直径的性质优化我们的染色操作,并提出最优的染色方案。
一、直径链的染色操作
考虑一条长度为 (d) 的链,链上的每个节点都需要染色,操作一次最多能染黑链上的 2 个点。我们从树的直径出发,考虑如何使用最少的操作将所有节点染黑。
1. 直径 (d) 为奇数
-
当直径 (d) 是奇数时,我们可以选择直径的中点 (u),然后进行一系列操作,操作的顺序是从 (u) 出发,染色 (u) 和与其距离为 (0, 1, 2, …, d-1) 的节点。这些操作的形式可以是:
[
(u, 0), (u, 1), (u, 2), …, (u, d-1)
]这样,通过最多 ( \frac{d+1}{2} ) 次操作,所有节点都能被染黑,因为每次操作都会把 2 个点染黑。
2. 直径 (d) 为偶数
-
当直径 (d) 为偶数时,我们面临的挑战是如何通过最少次数的操作,覆盖整棵树的所有节点。这里分为两种情况:
-
当 (d \mod 4 = 0)(即直径长度为 4 的倍数):
我们可以选择直径的中心边 ( (x, y) ),然后交替地进行以下操作:[
(x, 1), (y, 1), (x, 3), (y, 3), …, (x, d/2 - 1), (y, d/2 - 1)
]这样只需要 ( \frac{d}{2} ) 次操作。
-
当 (d \mod 4 = 2)(即直径长度为 2 或 6 的余数为 2):
由于不能完全通过交替操作来染色,我们只能从中心出发,进行如下操作:[
(x, 0), (x, 1), (x, 2), …, (x, d/2)
]这样需要 ( \frac{d}{2} + 1 ) 次操作。
-
二、整体思路
-
找直径:
- 通过两次 DFS 来找到树的直径。第一次 DFS 从任意节点出发,找到最远的节点 (A);第二次 DFS 从 (A) 开始,找到最远的节点 (B),则 (A) 到 (B) 的路径即为树的直径。
-
根据直径的长度选择操作策略:
- 如果直径 (d) 为奇数,从中点出发进行操作。
- 如果直径 (d) 为偶数,分为两种情况:
- 如果 (d \mod 4 = 0),通过中心边交替操作。
- 如果 (d \mod 4 = 2),从中心出发逐渐染色。
-
输出操作结果:
- 输出最少的操作次数和每次操作的具体节点及距离。
三、时间复杂度分析
- DFS 查找直径的时间复杂度是 (O(n)),每次 DFS 都需要遍历整个树的节点和边,最多遍历 (n-1) 条边。
- 操作计算 的时间复杂度是 (O(1)),因为操作次数由直径的长度确定,而直径已经通过 DFS 计算出来。
- 因此,每个测试用例的时间复杂度是 (O(n)),而给定 (T) 个测试用例,所有测试用例的总时间复杂度为 (O(T \cdot n))。题目保证了总节点数 (n) 不超过 2000,所以这是一个高效的解法。
四、代码实现
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
#define BoBoowen ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
using namespace std;const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;
const int N = 2e3 + 10;int n;
vector<int> g[N];
int fa[N];
int started;
int ended;
int height;
vector<int> rode;void dfs1(int x, int f, int h)
{for (auto it : g[x]){if (it == f){continue;}dfs1(it, x, h + 1);}if (h > height){height = h;started = x;}
}void dfs2(int x, int f, int h)
{fa[x] = f;for (auto it : g[x]){if (it == f){continue;}dfs2(it, x, h + 1);}if (h > height){height = h;ended = x;}
}void cleared()
{for (int i = 0; i <= n; ++i){g[i].clear();fa[i] = 0;}height = 0;rode.clear();
}void solved()
{cin >> n;for (int i = 0; i < n - 1; ++i){int x, y;cin >> x >> y;g[x].push_back(y);g[y].push_back(x);}dfs1(1, 0, 1);// cout << started << endl;height = 0;dfs2(started, 0, 1);int now = ended;while (now != 0){rode.push_back(now);now = fa[now];}// cout << ended << endl;// for (auto it : rode)// {// cout << it << ' ';// }// cout << endl;if (height % 2 == 1){cout << height / 2 + 1 << endl;for (int i = 0; i <= height / 2; ++i){cout << rode[height / 2] << ' ' << i << endl;}}else if (height % 4 == 0){cout << height / 2 << endl;for (int i = 1; i <= height / 2 - 1; i += 2){cout << rode[height / 2 - 1] << ' ' << i << endl;cout << rode[height / 2] << ' ' << i << endl;}}else{cout << height / 2 + 1 << endl;for (int i = 0; i <= height / 2; i++){cout << rode[height / 2 - 1] << ' ' << i << endl;}}cleared();
}signed main()
{BoBoowen;int T = 1;cin >> T;while (T--){solved();}
}
五、总结
- 树的直径是这道题的核心,利用树的直径来优化染色操作,可以大幅减少操作次数。
- 根据直径的长度,决定从中点出发进行染色或者采用交替操作,这样能够保证染色的最优性。
- 时间复杂度为 (O(n)),对于每个测试用例能够在合理时间内求解出最少的染色操作次数。
相关文章:
 ))
Tree Compass( Codeforces Round 934 (Div. 2) )
Tree Compass( Codeforces Round 934 (Div. 2) ) You are given a tree with n n n vertices numbered 1 , 2 , … , n 1, 2, \ldots, n 1,2,…,n. Initially, all vertices are colored white. You can perform the following two-step operation: …...

【Numpy核心编程攻略:Python数据处理、分析详解与科学计算】2.17 掩码数组:缺失值处理的优雅方案
2.17 掩码数组:缺失值处理的优雅方案 目录 #mermaid-svg-12vjJJbyudPnkYBO {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-12vjJJbyudPnkYBO .error-icon{fill:#552222;}#mermaid-svg-12vjJJbyudPnkYBO…...

PHP 常用函数2025.02
PHP implode() 函数 语法 implode(separator,array) 参数描述separator可选。规定数组元素之间放置的内容。默认是 ""(空字符串)。array必需。要组合为字符串的数组。 技术细节 返回值:返回一个由数组元素组合成的字符串。PHP 版…...

react中如何获取dom元素
实现代码 const inputRef useRef(null) inputRef.current.focus()...

【C++】继承(下)
大家好,我是苏貝,本篇博客带大家了解C的继承(下),如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 5.继承与友元6.继承与静态成员7.复杂的菱形继承及菱形虚拟继承8.继…...

C语言实现字符串排序:从代码到原理深度解析
在编程的世界里,字符串处理是一项基础且重要的技能。今天,我们通过分析一段C语言代码来深入了解如何对字符串进行排序。 一、代码呈现 #include <stdio.h> #include <string.h> int main() { char s[1001]; scanf("%s", s); int…...

Vue3的el-table-column下拉输入实时查询API数据选择的实现方法
由于本人对el-table-column有下拉输入选择的要求,根据网上搜索的资料及本人优化,推出我比较满意的方法,供各位读者参考使用。 效果图 el-table-column写法 <el-table-columnlabel"货品编号"align"center"prop"…...
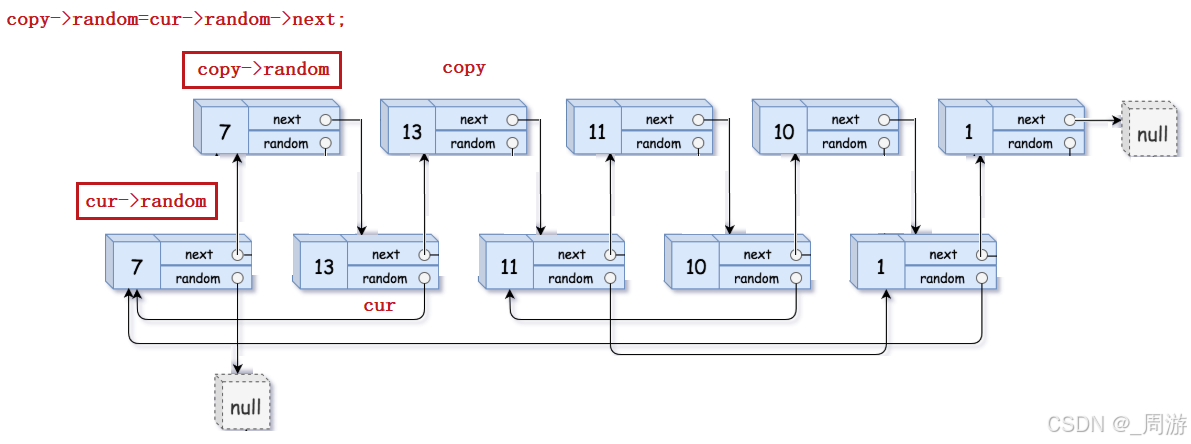
【数据结构】_链表经典算法OJ:复杂链表的复制
目录 1. 题目链接及描述 2. 解题思路 3. 程序 1. 题目链接及描述 题目链接:138. 随机链表的复制 - 力扣(LeetCode) 题目描述: 给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,…...

Vue 图片引用方式详解:静态资源与动态路径访问
目录 前言1. 引用 public/ 目录2. assets/ 目录3. 远程服务器4. Vue Router 动态访问5. 总结6. 扩展(图片不显示) 前言 🤟 找工作,来万码优才:👉 #小程序://万码优才/r6rqmzDaXpYkJZF 在 Vue 开发中&#x…...

chatGPT写的网页版贪吃蛇小游戏
chatGPT写的网页版贪吃蛇小游戏 前言网页版贪吃蛇小游戏 前言 之前无聊,让ChatGPT写了一段基于html语言的贪吃蛇小游戏代码 网页版贪吃蛇小游戏 将以下内容复制到记事本,重命名为xxx.html即可打开浏览器游玩 这里是一个使用HTML、CSS和JavaScript编写…...

Python量化交易助手:xtquant的安装与应用
Python量化交易助手:xtquant的安装与应用 技术背景和应用场景 在量化交易领域,Python因其强大的库支持和灵活性成为了许多开发者的首选语言。其中,xtquant 是迅投官方开发的一个Python包,专门用于与miniqmt通信,实现…...

前缀和算法
文章目录 算法总览题目1371.每个元音包含偶数次的最长子字符串 算法总览 题目 1371.每个元音包含偶数次的最长子字符串 1371.每个元音包含偶数次的最长子字符串 参考博主的讲解 思路分析:就是得使用前缀和记录情况,dp[i][j]表示s[0] 到s[i] 中&…...

Qt常用控件 输入类控件
文章目录 1.QLineEdit1.1 常用属性1.2 常用信号1.3 例子1,录入用户信息1.4 例子2,正则验证手机号1.5 例子3,验证输入的密码1.6 例子4,显示密码 2. QTextEdit2.1 常用属性2.2 常用信号2.3 例子1,获取输入框的内容2.4 例…...

《最小阻力之路》关于愿景的理解和思考
一、愿景的形成机制 1. 愿景的三层来源 来源层级形成机制案例潜在偏差风险① 本能冲动层对快感/痛苦的即时反应"想暴富"源于缺钱焦虑易被短期情绪劫持② 社会镜像层内化外界标准(家庭/社会/文化)"必须考研"因家人期待混淆他人需求…...

Ubuntu 22.04系统安装部署Kubernetes v1.29.13集群
Ubuntu 22.04系统安装部署Kubernetes v1.29.13集群 简介Kubernetes 的工作流程概述Kubernetes v1.29.13 版本Ubuntu 22.04 系统安装部署 Kubernetes v1.29.13 集群 1 环境准备1.1 集群IP规划1.2 初始化步骤(各个节点都需执行)1.2.1 主机名与IP地址解析1.…...

虚幻基础17:动画层接口
能帮到你的话,就给个赞吧 😘 文章目录 animation layer interface animation layer interface 动画层接口:动画图表的集。仅有名字。 添加到动画蓝图中,由动画蓝图实现动画图表。...

无人机PX4飞控 | PX4源码添加自定义uORB消息并保存到日志
PX4源码添加自定义uORB消息并保存到日志 0 前言 PX4的内部通信机制主要依赖于uORB(Micro Object Request Broker),这是一种跨进程的通信机制,一种轻量级的中间件,用于在PX4飞控系统的各个模块之间进行高效的数据交换…...

HTMLCSS :下雪了
这段代码创建了一个动态的雪花飘落加载动画,通过 CSS 技术实现了雪花的下落和消失效果,为页面添加了视觉吸引力和动态感。 大家复制代码时,可能会因格式转换出现错乱,导致样式失效。建议先少量复制代码进行测试,若未能…...

如何处理 Typecho Joe 主题被抄袭或盗版的问题
在开源社区中,版权保护是一个非常重要的话题。如果你发现自己的主题(如 Joe 主题)被其他主题(如子比主题)抄袭或盗版,你可以采取以下措施来维护自己的权益。 一、确认侵权行为 在采取任何行动之前…...

利用Vue和javascript分别编写一个“Hello World”的定时更新
目录 一、利用Vue编写一个“Hello World”的定时更新(1)vue编码在Html文件中(2)vue编码在js文件中 二、利用javascript编写一个“Hello World”的定时更新 一、利用Vue编写一个“Hello World”的定时更新 (1ÿ…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
