C++:高度平衡二叉搜索树(AVLTree) [数据结构]
目录
一、AVL树
二、AVL树的理解
1.AVL树节点的定义
2.AVL树的插入
2.1更新平衡因子
3.AVL树的旋转
三、AVL的检查
四、完整代码实现
一、AVL树
AVL树是什么?我们对 map / multimap / set / multiset 进行了简单的介绍,可以发现,这几个容器有个共同点是:其底层都是按照二叉搜索树来实现的。但是二叉搜索树有其自身的缺陷,假如往树中插入的元素有序或者接近有序,二叉搜索树就会退化成单支树,时间复杂度会退化成 O(N),因此 map、set 等关联式容器的底层结构是对二叉树进行了平衡处理,即采用平衡树来实现。

此二叉树插入元素有序,进行查找的时候效率会相当低下,甚至当接近为单支树的时候,查找效率会相当于在顺序表中的查找效率。因此俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis发明了一个解决方案:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。这也就是AVL树的由来。
一棵
AVL树或者是空树,或者是具有以下性质的二叉搜索树:1、它的左右子树都是AVL树
2、左右子树高度之差的绝对值不会超过1
左右子树的高度差也叫做平衡因子,在这样的树中进行搜索,时间复杂度是
O(logN)。
二、AVL树的理解
1.AVL树节点的定义
AVL 树节点是一个 三叉链结构,除了指向左右孩子的指针,还有一个指向其父亲的指针,数据域是键值对,即 pair 对象,还引入了平衡因子,用来判断是否需要进行平衡操作。
// AVL树节点的定义(KV模型)
template<class K, class V>
struct AVLTreeNode
{AVLTreeNode<T>* _left; // 该节点的左孩子AVLTreeNode<T>* _right; // 该节点的右孩子AVLTreeNode<T>* _parent; // 该节点的双亲指针pair<K, V> _kv; // 键值对int _bf; // 该节点的平衡因子(balance factor) = 右子树高度-左子树高度// 构造函数AVLTreeNode(const pari<K, V>& kv): _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};// AVL树的定义(KV模型)
template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:// 成员函数private:Node* _root;
}2.AVL树的插入
AVL 树就是在二叉搜索树的基础上引入了平衡因子,因此 AVL 树也可以看成是二叉搜索树。那么 AVL 树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点到 AVL 树中。
- 新节点插入后,AVL 树的平衡性可能会遭到破坏,此时就需要更新平衡因子,并检测是否破坏了 AVL 树的平衡(控制树的平衡(旋转操作))。
// 插入节点
bool Insert(const pair<K, V>& kv)
{// 如果树为空,则直接插入节点if (_root == nullptr){_root = new Node(kv);return true;}// 如果树不为空,找到适合插入节点的空位置Node* parent = nullptr; // 记录当前节点的父亲Node* cur = _root; // 记录当前节点while (cur) // while循环结束,说明找到适合插入节点的空位置了{if(kv.first > cur->_kv.first) // 插入节点键值k大于当前节点{parent = cur;cur = cur->_right;}else if(kv.first < cur->_kv.first) // 插入节点键值k小于当前节点{ parent = cur;cur = cur->_left;}else // 插入节点键值k等于当前节点{return false;}}// 插入新节点cur = new Node(kv); // 申请新节点// 判断当前节点是父亲的左孩子还是右孩子if (cur->_kv.first > parent->_kv.first){parent->_right = cur; }else{parent->_left = cur;}cur->_parent = parent;// 控制平衡// 1、更新平衡因子// ...return true;
}2.1更新平衡因子
(1) 插入新节点cur 插入后,AVL树的平衡性可能会遭到破坏,引入平衡因子的意义也就在于此,parent 的平衡因子一定需要调整,在插入之前,parent 的平衡因子分为三种情况:-1,0,1,分以下两种情况:
①如果插入到 新节点父亲(parent)的左侧,只需给父亲(parent)的平衡因子--(
_bf--)即可。②如果插入到 新节点父亲(parent)的右侧,只需给父亲(parent)的平衡因子++(_bf++)即可。
(2) 新节点父亲的平衡因子更新以后,又会分为 3 种情况:
①如果更新以后,parent 的平衡因子是 0(则说明插入之前 parent 的平衡因子之前一定为 1/-1),说明父亲所在子树高度没变(因为把矮的那边给填补上了),此时满足 AVL 树的性质,插入成功,不需要继续往上更新。
②如果更新以后,parent 的平衡因子是 1/-1(则说明插入之前 parent 的平衡因子 一定为 0),说明父亲所在子树高度增加,需要继续往上更新。(最坏情况:往上一直更新到根节点)。
③如果更新以后,parent 的平衡因子是 2/-2,说明父亲所在子树出现了不平衡,需要对其进行旋转处理。

根据此理解可以写出代码来更新平衡因子:
// 插入节点
bool Insert(const pair<K, V>& kv)
{// 控制平衡// 1、更新平衡因子while (parent) // 最坏情况:更新到根节点{// 更新双亲的平衡因子if (cur == parent->_left) // 新节点插入在父亲的左边parent->_bf--;else // 新节点插入在父亲的右边parent->_bf++;// 更新后检测双亲的平衡因子if (0 == pParent->_bf){ break;}//else if (1 == parent->_bf || -1 == parent->_bf)else if (abs(parent->_bf) == 1) // 插入前双亲的平衡因子是0,插入后双亲的平衡因为为1 或者 -1 ,说明以双亲为根的二叉树的高度增加了一层,因此需要继续向上调整{cur = parent;parent = cur->_parent;}else if (abs(parent->_bf) == 2) // 双亲的平衡因子为正负2,违反了AVL树的平衡性,需要对以parent为根的树进行旋转处理{// 1、父节点的右边高,左边低,需要往左旋if (parent->_bf == 2 && cur->_bf == 1) {RotateL(parent); // 左单旋}// 2、父节点的左边高,右边低,需要往右旋else if ((parent->_bf == -2 && cur->_bf == -1)){RotateR(parent); // 右单旋}// 3、父节点的左边高,且父节点左孩子的右边高else if (parent->_bf == -2 && cur->_bf == 1) {RotateLR(parent); // 左右双旋}// 4、父节点的右边高,且父节点右孩子的左边高else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent); // 右左双旋}break; // 旋转完成,树已平衡,退出循环}// 除了上述3种情况,平衡因子不可能有其它的值,报错处理else{assert(false);}}return true;
}3.AVL树的旋转
那当上面的情况已经发生,AVL树应该如何进行平衡?这就引入了旋转的概念,旋转是在遵循二叉搜索树的规则下,让左右均衡,降低整颗树的高度。
在AVL树中,当破坏了AVL树的平衡后,总共有四种会引发的旋转:
1. 新节点插入较高左子树的左侧,引发右单旋

[操作]
1、让 subL 的右子树 subLR 成为 parent 的左子树(因为 subLR 的右子树根节点值 > 30,< 60)。
2、让 parent 成为 subL 的右子树(因为 60 > 30)。
3、让 subL 变成这个子树的根。这一步操作前需要先判断下:parent 是根节点,还是一个普通子树
- 如果是根节点,旋转完成后,则更新 subL 为新的根节点。
- 如果是普通子树(可能是某个节点的左子树,也可能是右子树,这里作一个判断),然后更新 subL 为这个子树的根节点。
4、根据树的结构,更新 parent 和 subL 的平衡因子为 0。
在旋转过程中,更新双亲指针的指向,有以下几种情况需要考虑:
- 30 节点的右孩子可能存在,也可能不存在。(subL 的右子树 subLR 可能存在,也可能为空。当不为空时才更新 subL 右子树 subLR 的双亲指针指向)。
- 60 可能是根节点,也可能是子树。(旋转完成后,subL 的双亲节点,可能是空,也可能是 parent 原先的父节点。所以在更新 subL 的双亲指针前需要判断下)。
依次调整 subLR、parent、subL 的位置和双亲指针的指向,下面为右单旋代码:
// 右单旋
void _RotateR(Node* parent)
{ Node* subL = parent->_left; // subL : parent的左孩子Node* subLR = subL->_right; // subLR : parent左孩子的右孩子// 旋转完成之后,让subL的右子树subLR成为parent的左子树parent->_left = subLR;// 如果subLR存在,更新subLR的双亲指针,指向parentif (subLR){subLR->_parent = parent;}// 因为parent可能是棵子树,因此在更新其双亲前必须先保存parent的父节点Node* ppNode = parent->_parent;// 让parent成为subL的右子树subL->_right = parent;// 更新parent的双亲指针,指向subLparent->_parent = subL;// 如果parent是根节点,根新指向根节点的指针if (_root == parent){_root = subL; // 更新subL为新的根subL->_parent = nullptr; // 更新subL的双亲指针,指向空}// parent不是根节点,就是一个普通子树else{// 判断parent原先是左孩子还是右孩子if (ppNode->_left == parent){ppNode->_left = subL; // parent原先的双亲节点接管subL,subL为这个子树的根}else{ppNode->_right = subL;}subL->_parent = ppNode; // 更新subL的双亲指针}// 根据调整后的结构更新部分节点的平衡因子parent->_bf = pSubL->_bf = 0;
}2. 新节点插入在较高右子树的右侧,引发左单旋

[操作]
1、让 subR 的左子树 subRL 成为 parent 的右子树(因为 subRL 的左子树根节点值 > 30,< 60)。
2、让 parent 成为 subR 的左子树(因为 30 < 60)。
3、让 subR 变成这个子树的根。这一步操作前需要先判断下:parent 是根节点,还是一个普通子树
- 如果是根节点,旋转完成后,则更新 subR 为新的根节点。
- 如果是普通子树(可能是某个节点的左子树,也可能是右子树,这里作一个判断),然后更新 subR 为这个子树的根节点。
4、根据树的结构,更新 parent 和 subR 的平衡因子为 0。
在旋转过程中,更新双亲指针的指向,有以下几种情况需要考虑:
- subR 的左子树 subRL 可能存在,也可能为空。(当不为空时才更新 subR 左子树 subRL 的双亲指针指向)。
- 旋转完成后,subR 的双亲节点,可能是空,也可能是 parent 原先的父节点。(所以更新 subR 的双亲指针前需要判断下)。
依次调整 subRL、parent、subR 的位置和双亲指针的指向,左单旋代码:
// 左单旋
void treeRotateLeft(Node* parent)
{Node* subR = parent->_right; // subR:父亲的右孩子Node* subRL = subR->_left; // subRL:父亲的右孩子的左孩子(大于父亲,小于subR)// 让subRL成为父亲的右子树parent->_right = subRL;// 如果subRL不为空if (subRL){subRL->_parent = parent; // 更新subRL双亲指针,指向parent}// 因为parent可能是棵子树,因此在更新其双亲前必须先保存parent的父节点Node* ppNode = parent->_parent;// 让parent成为subR的左子树subR->_left = parent; // 更新parent双亲指针的指向parent->_parent = subR;// 判断parent是不是根节点if (parent == _root){_root = subR; // subR为新的根subR->_parent = nullptr; // subR双亲指针指向空}// 不是根节点,就是一个普通子树else{// 判断parent原先是左孩子还是右孩子if (ppNode->_left == parent){ppNode->_left = subR; // parent原先的双亲节点接管subR,subR为这个子树的根}else{ppNode->_right = subR;}subR->_parent = ppNode; // 更新subR的双亲指针}// 根据树的结构,更新parent和subR的平衡因子parent->_bf = subR->_bf = 0;
}3. 新节点插入较高右子树的左侧,引发先右单旋再左单旋
将新的节点插入到了 parent 右孩子的左子树上,导致的不平衡的情况。这时我们需要的是先对 parent 的右孩子进行一次右旋,再对 parent 进行一次左旋。

左右双旋操作后,根据树的结构,更新平衡因子时,需要注意:
插入新节点的位置不同,经过右左双旋后,得到树的结构也会有所不同,平衡因子也会有所不同,有以下三种情况:
- 新节点插入到了 parent 右孩子的左子树的左边。
- 新节点插入到了 parent 右孩子的左子树的右边。
- 新节点就是 parent 右孩子的左孩子。
这里可以观察到一个现象,根据这个现象就很好推出旋转后的平衡因子:
节点 60 的左右子树被分走了,左子树 b 最终成了节点 30 的右子树,右子树 c 最终成了节点 90 的左子树。

// 右左双旋
void treeRotateRL(Node* parent)
{Node* subR = parent->_right; // 记录parent的右孩子Node* subRL = subR->_left; // 记录parent的右孩子的左孩子// 旋转之前,因为插入新节点的位置不同,subRL的平衡因子可能为-1/0/1int bf = subRL->_bf; // 记录subRL的平衡因子RotateR(parent->_right); // 先对parent的右孩子进行右单旋RotateL(parent); // 再对parent进行左单选// 旋转完成之后,根据树的结构对其他节点的平衡因子进行调整subRL->_bf = 0;if (bf == -1){parent->_bf = 0;subR->_bf = 1;}else if (bf == 1){parent->_bf = -1;subR->_bf = 0;}else if(bf == 0){parent->_bf = 0;subR->_bf = 0;}else{assert(false);}
}4. 新节点插入较高左子树的右侧,引发先左单旋再右单旋
将新的节点插入到了 parent 左孩子的右子树上,导致的不平衡的情况。这时我们需要的是先对 parent 的右孩子进行一次左旋,再对 parent 进行一次右旋。
void _RotateLR(PNode pParent)
{Node* subL = parent->_left; // 记录parent的左孩子Node* subLR = subL->_right; // 记录parent的左孩子的右孩子// 旋转之前,因为插入新节点的位置不同,subLR的平衡因子可能是-1/0/1int bf = subLR->_bf; // 记录subLR的平衡因子// 先对parent的左孩子进行左单旋RotateL(parent->_left);// 再对parent进行右单旋RotateR(parent);// 旋转完成之后,根据情况对其他节点的平衡因子进行调整subLR->_bf = 0;if (bf == -1){parent->_bf = 1;subL->_bf = 0;}else if (bf == 1){parent->_bf = 0;subL->_bf = -1;} else if (bf == 0){parent->_bf = 0;subL->_bf = 0;}else{assert(false);}
}【总结】
假如以 parent 为根的子树不平衡,即 parent 的平衡因子为 2/-2,分以下情况考虑:
1、parent 的平衡因子为 2,说明 parent 的右子树高,设 parent 的右子树的根为 subR。
- 当 subR 的平衡因子为 1 时,执行左单旋。
- 当 subR 的平衡因子为 -1 时,执行右左双旋。
2、parent 的平衡因子为 -2,说明 parent 的左子树高,设 parent 的左子树的根为 subL。
- 当 subL 的平衡因子为 -1 时,执行右单旋。
- 当 subL 的平衡因子为 1 时,执行左右双旋。
旋转完成后,原 parent 为根的子树个高度降低,已经平衡,不需要再向上更新。
三、AVL的检查
依据上面的实现可以基本实现AVL树,那如何验证AVL树是否正确?其实验证也很简单,只需要看每个节点的平衡因子是否等于对应的右子树减左子树的值即可。
// 计算当前树的高度
int Height(Node* root)
{// 当前树为空,则高度为0if (root == nullptr)return 0;// 当前树的高度 = 左右子树中高度最大的那个加1return max(Height(root->_left), Height(root->_right)) + 1;
}// 保持树的封装 进行检查AVL树
bool IsBalance1()
{return _IsBalance(_root);
}// 进行检查AVL树
bool _IsBalance1(Node* root)
{// 当前树为空,说明是平衡的if (root == nullptr)return true;// 当前树不为空,计算左右子树的高度int leftHT = Height(root->_left);int rightHT = Height(root->_right);int diff = rightHT - leftHT;if (diff != root->_bf) // 检查当前树的平衡因子是否计算正确{cout << root->_kv.first << "平衡因子异常" << endl;return false;}// 左右子树高度相减的绝对值小于2,说明当前树是平衡的,则继续往下判断其它子树return abs(diff) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);
}四、完整代码实现
#pragma oncetemplate<class K, class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;//三叉链AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;//平衡因子pair<K, V> _kv;//key//构造函数AVLTreeNode(const pair<K, V>& kv): _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){//1.先按二叉搜索树的规则插入if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){paretn = cur;cut = cur->_right;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//2.更新平衡因子while (parent)//有可能要更新到根节点{if (cur == parent->_right){parent->_bf ++;}else{parent->_bf--;}if (parent->_bf == 0){//没变,更新结束break;}else if (parent->_bf == 1 || parent->_bf == -1){//说明所在子树的高度变了,继续往上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//parent 的子树出现不平衡了,需要旋转处理}}return true;}//左单旋void RotateL(Node* parent){/*Node* subR = parent->_right;parent->_right = subR->_left;subR->_left = parent;*///没有处理每个节点的parent,Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppNode = parent->_parent;parent->_parent = subR;//1.原来的parent是这棵树的根,现在subR是树的根//2.parent不是整棵树的根,那么链接关系要变,subR就要顶替parent的位置if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent)ppNode->_left = subR;elseppNode->_right = subR;subR->_parent = ppNode;}parent->_bf = subR->_bf = 0;}//右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppNode = parent->_parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent)PPNode->_left = subL;elseppNode->_right = subL;subL->_parent = ppNode;}subL->_bf = parent->_bf = 0;}// 先右单旋再左单旋void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 0){// 自己就是新增的节点parent->_bf = subR->_bf = 0;}else if (bf == -1){// 在左子树进行的插入parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else if (bf == 1){// 在右子树进行的插入subRL->_bf = 0;subR->_bf = 0;parent->_bf = -1;}else{assert(false);}}// 先进行左单旋,再进行右单旋void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(subL);RotateR(parent);// 更换平衡因子if (bf == 0){subL->_bf = subLR->_bf = 0;}else if (bf == 1){// 插入在右子树subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else if (bf == -1){// 插入在左子树parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else{assert(false);}}// 用于检查树的高度int TreeHeight(Node* root){if (root == nullptr)return 0;int leftheight = TreeHeight(root->_left);int rightheight = TreeHeight(root->_right);return max(leftheight, rightheight) + 1;}// 保持树的封装 进行检查AVL树bool IsBalance(){return _IsBalance(root);}// 进行检查AVL树bool _IsBalance(Node* root){if (root == nullptr)return true;int leftheight = TreeHeight(root->_left);int rightheight = TreeHeight(root->_right);if (rightheight - leftheight != root->_bf)return false;return abs(rightheight - leftheight) < 2 && _IsBalance(root->_left) && _IsBalance(root->_right);}private:Node* _root = nullptr;
};【总结】
AVLTree 高度平衡二叉搜索树。
1.搜索树
2.要求树的左右子树的高度差不超过1,树的左子树和右子树也满足高度差不超过1,(树及所有子树都要满足前面的要求)
3.为了方便实现,引入了平衡因子(这个只是一种方式,并不是必须要这种)
4.平衡因子 = 右子树的高度 - 左子树的高度
5.高度基本可以控制在O(logN)
6.AVLTree增删查改的效率就是O(logN)
7.平衡因子到底是用来干嘛的?
8.AVLTree 的插入三步:
- 按二叉搜索树方式插入
- 更新平衡因子
- 如果更新完,没有违反规定,则插入结束,有违规,则旋转处理
9.不是所有的平衡因子都会被影响,被影响的是祖先,沿着路径往根节点更新祖先节点的平衡因子,但也不是所有的祖先都会被影响。
1.cur 是 parent 的左,parent->bf--,cur 是 parent 的右, parent->bf++,
2.更新完parent的bf 后,如果parent->bf == 0 ,说明parent的高度不变,更新结束,插入完成
解释: 说明更新前,parent 的 bf 是 -1 or 1, 现在变成0, 说明把矮的那边子树给填上了,说明高度没有变,对上层没有影响
3.更新完parent 的 bf 后, 如果parent->bf == 1 or -1 , 说明parent 的高度变了,继续往上更新
解释: 说明跟新前,parent 的 bf 是 0 , 现在变成了 1 or -1, 说明 一边高,对上层有影响,继续往上更新。
4.再次更新完,parent 的 bf === -2 or 2 说明parent所在的子树出现了不平衡,需要旋转处理
5.旋转处理:
- 旋转完后,还得是搜索树
- 旋转之后能把它变成平衡(左子树,右子树高度差不超过1)(左单旋,右单旋)
相关文章:

C++:高度平衡二叉搜索树(AVLTree) [数据结构]
目录 一、AVL树 二、AVL树的理解 1.AVL树节点的定义 2.AVL树的插入 2.1更新平衡因子 3.AVL树的旋转 三、AVL的检查 四、完整代码实现 一、AVL树 AVL树是什么?我们对 map / multimap / set / multiset 进行了简单的介绍,可以发现,这几…...

建筑兔零基础自学python记录18|实战人脸识别项目——视频检测07
本次要学视频检测,我们先回顾一下图片的人脸检测建筑兔零基础自学python记录16|实战人脸识别项目——人脸检测05-CSDN博客 我们先把上文中代码复制出来,保留红框的部分。 然后我们来看一下源代码: import cv2 as cvdef face_detect_demo(…...

【MySQL数据库】Ubuntu下的mysql
目录 1,安装mysql数据库 2,mysql默认安装路径 3,my.cnf配置文件? 4,mysql运用的相关指令及说明 5,数据库、表的备份和恢复 mysql是一套给我们提供数据存取的,更加有利于管理数据的服务的网络程序。下…...
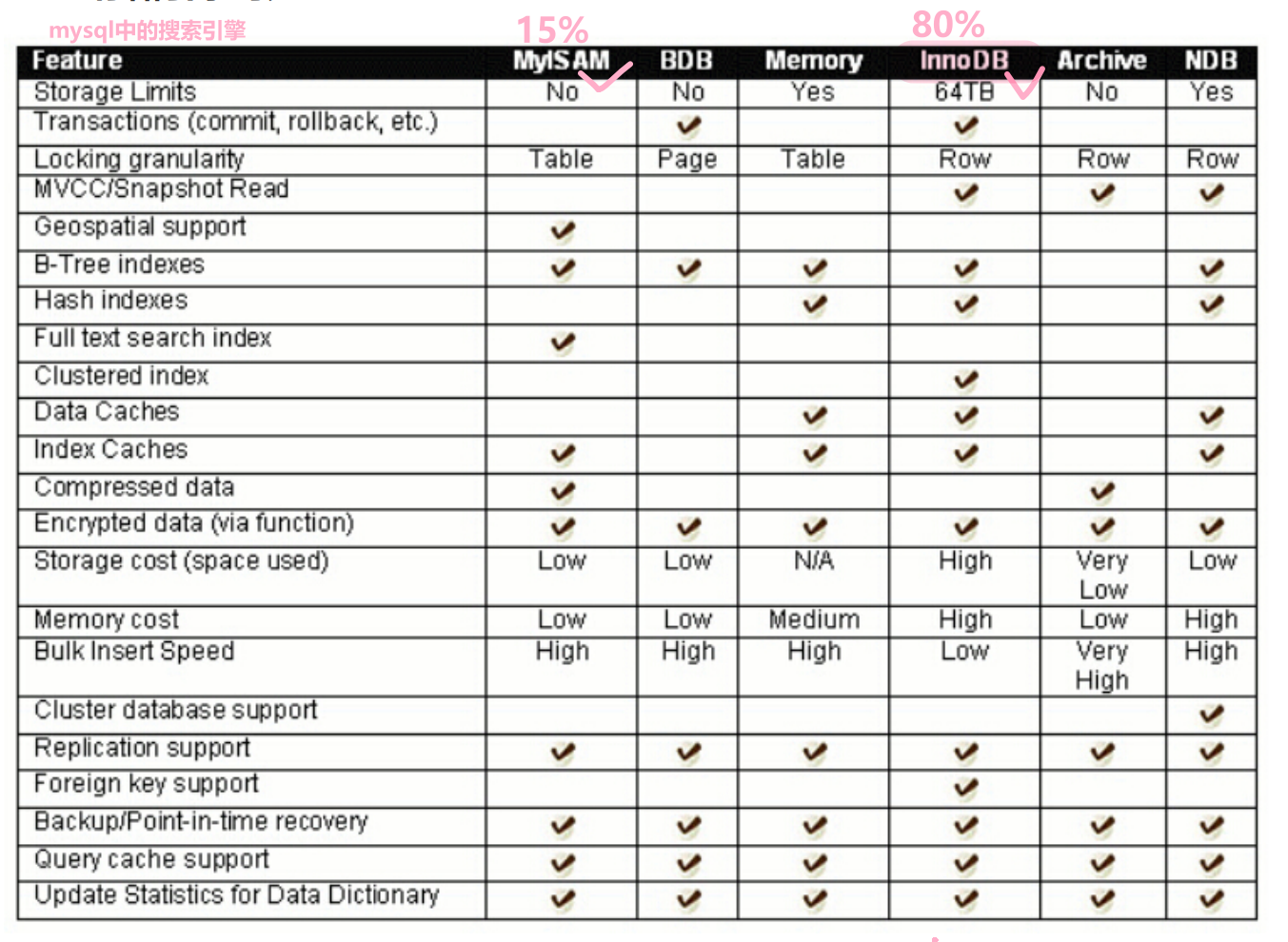
[MySQL#1] database概述 常见的操作指令 MySQL架构 存储引擎
#1024程序员节|征文# 目录 一. 数据库概念 0.连接服务器 1. 什么是数据库 口语中的数据库 为什么数据不直接以文件形式存储,而需要使用数据库呢? 总结 二. ??基础操作 三. 主流数据库 四. 基础知识 服务器,数据库&…...

1.从零开始学会Vue--{{基础指令}}
全新专栏带你快速掌握Vue2Vue3 1.插值表达式{{}} 插值表达式是一种Vue的模板语法 我们可以用插值表达式渲染出Vue提供的数据 1.作用:利用表达式进行插值,渲染到页面中 表达式:是可以被求值的代码,JS引擎会将其计算出一个结果 …...

VS2022中.Net Api + Vue 从创建到发布到IIS
VS2022中.Net Api Vue 从创建到发布到IIS 前言一、先决条件二、创建项目三、运行项目四、增加API五、发布到IIS六、设置Vue的发布 前言 最近从VS2019 升级到了VS2022,终于可以使用官方的.Net Vue 组合了,但是使用过程中还是有很多问题,这里记录一下. 一、先决条件 Visual …...

RFID技术在制造环节的应用与价值
在现代制造业中,信息化和智能化已经成为企业提升竞争力的重要手段。RFID技术因其非接触式、远距离和高效识别的特点,广泛应用于生产的多个环节。本文将详细解读生产过程中RFID的关键应用场景,并结合实际案例,展示其为制造业带来的…...

(前端基础)HTML(一)
前提 W3C:World Wide Web Consortium(万维网联盟) Web技术领域最权威和具有影响力的国际中立性技术标准机构 其中标准包括:机构化标准语言(HTML、XML) 表现标准语言(CSS) 行为标准…...

Linux文件管理:硬链接与软链接
文章目录 1. 硬链接的设计目的(1)节省存储空间(2)提高文件管理效率(3)数据持久性(4)文件系统的自然特性 2. 软链接的设计目的**(1)跨文件系统引用****&#x…...

pnpm, eslint, vue-router4, element-plus, pinia
利用 pnpm 创建 vue3 项目 pnpm 包管理器 - 创建项目 Eslint 配置代码风格(Eslint用于规范纠错,prettier用于美观) 在 设置 中配置保存时自动修复 提交前做代码检查 husky是一个 git hooks工具(git的钩子工具,可以在特定实际执行特…...

在软件产品从开发到上线过程中,不同阶段可能出现哪些问题,导致软件最终出现线上bug
在软件产品从开发到上线的全生命周期中,不同阶段都可能因流程漏洞、技术疏忽或人为因素导致线上问题。以下是各阶段常见问题及典型案例: 1. 需求分析与设计阶段 问题根源:业务逻辑不清晰或设计缺陷 典型问题: 需求文档模糊&#…...

Spring Boot中如何自定义Starter
文章目录 Spring Boot中如何自定义Starter概念和作用1. 概念介绍2. 作用和优势2.1 简化依赖管理2.2 提供开箱即用的自动配置2.3 标准化和模块化开发2.4 提高开发效率2.5 提供灵活的配置覆盖3. 应用场景创建核心依赖1. 确定核心依赖的作用2. 创建 starter-core 模块2.1 依赖管理…...

制作Ubuntu根文件
系列文章目录 Linux内核学习 Linux 知识(1) Linux 知识(2) WSL Ubuntu QEMU 虚拟机 Linux 调试视频 PCIe 与 USB 的补充知识 vscode 使用说明 树莓派 4B 指南 设备驱动畅想 Linux内核子系统 Linux 文件系统挂载 QEMU 通过网络实现…...

SpringBoot快速接入OpenAI大模型(JDK8)
使用AI4J快速接入OpenAI大模型 本博文给大家介绍一下如何使用AI4J快速接入OpenAI大模型,并且如何实现流式与非流式的输出,以及对函数调用的使用。 介绍 由于SpringAI需要使用JDK17和Spring Boot3,但是目前很多应用依旧使用的JDK8版本&…...
UniApp 中制作一个横向滚动工具栏
前言 最近在用 UniApp 开发项目时,需要一个横向滑动的工具栏。常见的工具栏一般都是竖着的,但横向滑动的工具栏不仅能展示更多内容,还能让界面看起来更加丰富。不过很多朋友可能会发现,如何让内容“横着”展示又不变形、能流畅滚…...

react中如何获取真实的dom
在 React 中,获取真实的 DOM 元素通常通过 ref 来实现。ref 是一个特殊的属性,用于引用组件或 DOM 元素的实例。你可以通过 ref 获取到组件的真实 DOM 元素或组件实例。 1. 函数组件中的 useRef 在函数组件中,获取 DOM 元素的引用需要使用 …...

5G与物联网的协同发展:打造智能城市的未来
引言 随着科技的不断进步,智能城市的概念已经不再是科幻小说中的幻想,它正在逐步走进我们的生活。而这背后的两大驱动力无疑是 5G和 物联网(IoT)。5G网络以其高速率、低延迟、大容量的优势,与物联网的强大连接能力相结…...

【Qt】实现定期清理程序日志
在现有Qt程序中实现可配置日志保存天数的代码示例,分为界面修改、配置存储和核心逻辑三部分: // 1. 在配置文件(如settings.h)中添加保存天数的配置项 class Settings { public:int logRetentionDays() const {return m_settings…...

git bisect 使用二分法查找引入错误的提交
git bisect 使用二分法查找引入错误的提交 Git bisect 命令官方文档 git bisect 这个命令使用二分搜索算法来查找项目历史中哪个提交引入了一个错误 使用该命令时,首先告诉它一个已知包含错误的 “坏” 提交 以及一个已知在错误出现之前的 “好” 提交 然后 git b…...

一种面向车载时间敏感网络的联合路由与时隙调度负载均衡算法
论文标题 中文标题:一种面向车载时间敏感网络的联合路由与时隙调度负载均衡算法 英文标题:A Joint Routing and Time-Slot Scheduling Load Balancing Algorithm for In-Vehicle TSN 作者信息 Bo Xu, Xinrui Chang, Dongyang Xu, Shuo Wang, Uzair As…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
