滑动窗口算法篇:连续子区间与子串问题

1.滑动窗口原理
那么一谈到子区间的问题,我们可能会想到我们可以用我们的前缀和来应用子区间问题,但是这里对于子区间乃至子串问题,我们也可以尝试往滑动窗口的思路方向去进行一个尝试,那么说那么半天,滑动窗口是什么呢?它怎么用呢?
滑动窗口这名字看起来很高大尚,但是实际上所谓的滑动窗口,就是维护两个指针left和right,那么这两个指针中间的内容就是我们的窗口,那么至于所谓的“滑动”,那么我们可以通过移动我们的左右两个指针来达到让这个窗口的沿着数组移动。
那么介绍完我们滑动窗口是什么,我再来说一下滑动窗口怎么用,对于滑动窗口问题,其实这类问题的解决的思想我觉得和我们的二分答案法的一个思想其实是有一点相近的,首先我们滑动窗口的题通常有一个特征,那么就是找一个子数组或者子串,但是我们找的这个子数组或者子串不是一般的子数组或者子串,它通常是要满足一个性质,并且我们要寻找的该子串是满足性质的一个边界点。
那么我们会定义一个滑动窗口也就是左指针与右指针,这个窗口内要维护的内容通常要满足这个性质,并且该性质与我们的窗口的长度存在一种单调性,窗口长度增大,那么意味着越容易达到满足该性质,反之长度越小,则不容易达到满足该性质,那么滑动窗口的长度扩大就是通过让右指针向右移动从而扩大右边界,那么当我们的滑动窗口内的内容达到该性质的时候,那么这就和我上文说的我们要寻找的子串有关,我们的目标子串不仅是满足该性质,而且是满足该性质的一个边界,所以这里我们滑动窗口内达标的一个子串它虽然满足该性质,但是它不一定是满足该性质的一个边界,由于我们窗口长度减小,那么越不容易达到该性质,那么我们此时就缩小左边界,也就是左指针往左移动,那么此时我们窗口长度在减小,那么我们就会缩小到该内容达到性质边界点的位置

那么我们滑动窗口的性质与窗口的长度的单调性不一定是长度越长越容易达到该性质,也可能是长度越长越不容易达到该性质,那么这得看具体题目,那么我们滑动窗口的原理总结来说就是:
首先识别这是一个子数组或者子串问题,并且要求的子数组与子串是满足特定性质的边界,那么我们就定义左右两个指针接着确定我们这个窗口里面的内容要维护要达到的性质,然后确定该性质与窗口长度的单调性。
那么相信你看完滑动窗口的原理你肯定还是一知半解的感觉,但没关系,接下来下文我会通过几道题来具体给你阐述我是如何通过滑动窗口的一个算法思想以及原理来解决这类题目的,以及该算法的大致处理流程是什么,那么不要走开,希望你耐心看完,相信我,你一定会理解并掌握该算法的思想。
2.应用
题目一:累加和>=k的长度最小的子数组 难度:EZ
题目:现在我们有一个数组,那么数组内的元素全部都为正数,那么我们要求累加和大于等于k的长度最小的子数组。
题目思路:那么这里看到子数组与子串首先就得敏感起来,那么这题的解法有很多,对于我想到的就有三个,如果还有其他算法能够解决该题的,欢迎在评论区补充,那么我们这题肯定可以通过滑动窗口来解决,还可以通过前缀和来解决,也还可以用二分答案法来解决。
那么这题我就讲一下我们的滑动窗口怎么做这道题,以及我是如何运用上面的算法思想的,那么这里我们分析一下题目,首先根据题目我们的子数组是满足某种性质,该性质就是累加和大于等于k,但是为什么该子数组就是特殊的子数组呢,因为我们要寻找的目标子数组是累加和大于等于k的长度最小的子数组,特殊就特殊在它要长度最小最小,也就意味着我们有很多满足该性质也就是累加和大于等于k的子数组,但是它的长度在其中不一定是最小,而这里所谓的最小,就是我们所说的满足该性质的一个边界,那么满足该性质的边界的子数组就是我们要得到的目标子数组。
那么接下来我们就定义一个滑动窗口,第二步就是确定我们该窗口里面的内容要满足的性质,那么对于这题来说,我们该窗口里的内容要满足的性质就是累加和大于等于k,那么我们再来分析该性质与窗口长度的单调性关系,那么我们知道由于数组内的元素都是正数,那么意味着我们窗口长度越大,那么我们窗口的累加和越大,那么就越容易达到满足我们窗口要维护的性质也就是大于等于k。
那么最开始我们的窗口的初始话是在数组的左边界,窗口长度为1,左右指针都指向下标为0的元素,也就是窗口内现在只有下标为0的元素(注意这里我们定义的窗口的左右边界是是左闭右闭的区间[L,R],如果你定义的是左闭右开[L,R)的区间的窗口的话,那么初始化窗口的右指针就该指向下标为1的位置),那么我们窗口如果不满足该性质的话,那么我们就往右扩,那么直到我们窗口内的内容达标,那么此时窗口内的内容是累加和大于等于k的子数组,但是该子数组不一定就是最小的子数组,也就是它不一定就落在性质的边界位置处,所以此时我们缩小我们的窗口,左指针向左移动,那么直到我们达到如果左指针在往左移动一步,那么该窗口的内容就不满足该性质也就是累加和大于等于k,那么这就找到了满足该性质的边界以右边界位置处结尾的子串,那么我们记录答案,我们就重复上面的步骤,一旦我们窗口达标,那么我们就尝试缩小,那么最后记录的答案就是最终结果。
代码实现:
class solution
{public:int minlengtharray(vector<int>& arr,int k){int l=0,r=0;int sum=0;int ans=INT_MAX;while(r<arr.size()){sum+=arr[r];if(sum<k){r++;}else{//当窗口内的和大于等于k时,尝试缩小窗口while(sum>=k&&l<=r){sum-=arr[l];l++;}ans=min(ans,r-l+1);}}return ans;}
}
那么这里我们说完解题思路,我们再来看看我们的滑动窗口是如何应用的,我们首先确定了我们的目标子数组满足的性质也就是累加和大于等于k并且它是满足该性质的边界因为要求最小长度的、,然后定义窗口,确定窗口要满足的性质以及与窗口长度的单调性关系,那么对于本体来说,窗口长度越大越容易满足该性质,接着就是不断的扩大以及缩小窗口,那么我们在此过程中,我们的左右指针是不会回退的,那么对于该题滑动窗口算法的时间复杂度就是遍历该数组的时间复杂度也就是o(N),那么滑动窗口也是解决该题的最优算法。
知道了这题怎么做以及滑动窗口的原理,那么这里我有一个思考题,读者可以先自行思考一下,我会在下文给出答案与解释。
那么假设我们这个数组里面的元素不全为正数而是有负数存在,那么请问该题还能用滑动窗口做吗?
答案是不行的,因为我们如果数组中有负数的话,那么此时我们窗口要维护要达到的性质也就是累加和大于等于k与我们的窗口长度的单调性就丧失了,那么我们窗口长度越大,我们知道如果数组的元素全是正式,那么窗口长度增大,窗口的累加和只可能增大,但是一旦有了负数的存在,我们窗口的长度增大,那么我们该窗口内的内容的累加和可能会增大可能会减小,所以不能应用,那么有负数的情况就只能用我们的前缀和来做了。
那么总结下来,滑动窗口算法的流程:
1.确定答案满足的性质
2.定义窗口,确定窗口要维护的性质,以及该性质与窗口长度的单调性关系
3.不满足窗口性质往右扩大,达到性质那么就从左边界缩小,记录答案
题目二:无重复字符的最长子串 难度:MID
题目:现在有一个字符串,我们要找到该字符串的无重复字符的最小子串,返回这个子串,题目保证一定有有重复子串
题目分析:那么这里这道题看到子串先考虑一下滑动窗口,那么这里这里我们的子串满足的性质是无重复字符,并且要找的该子串是性质的边界,那么我们还是定义一个窗口,然后确定该窗口要维护的性质是里面的内容是无重复字符,那么我们分析单调性,那么我们扩大窗口,窗口长度增大,那么字符数量增大,那么越不容易满足该性质,反之窗口长度越小则容易满足性质,那么这题和我们之前普遍的单调性是反着来的。
那么我们还是一样,往有扩大窗口,每次扩大的时候,那么我们都尝试能否缩小窗口,那么我们这里则比较当前右边界i位置的字符,那么找i位置的字符右侧之前出现过的最晚位置在不在窗口里面,如果在的话,说明有重复,那么我们就只能缩小左边界到该该位置的下一位,如果不在,那么则继续往右扩大。每一次扩充都得检查,让我们窗口里面维护的是无重复字符的子串
代码实现:
class solution
{public:void maxlengthstring(string& a,string& ans){int l=0,r=0;unordered_map<char,int> value;int start=0;int len=-1;while(r<a.size()){if(value.find(a[r])!=a.end()){if(a[r]>=l){l=a[r]+1;}if(len<r-l+1){len=r-l+1;start=l;}}value[a[r]]=r;r++;}ans=a.substr(start,len);return ans;}
}
题目三:寻找满足特定数量的字符的最小长度子串 难度:MID
题目:现在有一个字符串,我们要找到满足特定数量字符的最小子串。
注:我们这里的子串只要求满足特定数量的字符,其中可以包含其他字符,比如现在要找含有2个a,3个b的最小子串,那么对于该子串aabbbee是符合性质的
题目思路:那么这里我们子串的性质是要满足特定数量的字符,那么这里我们可以定义一个窗口,维护的性质就是满足特定数量的字符,那么我们窗口长度越大,那么越容易满足该性质,反之窗口长度越小则越不容易满足该性质,那么这里我们可以准备一张哈希表记录特定字符需要的数量,以及我们定义一个变量debt来表示需要的总数量,那么我们往右扩充窗口的时候,我们检查该窗口的右边界位置是否是特定字符,那么是的话,就在哈希表中的记录减一,然后总数量减一。
那么沃恩这道题得注意我们缩小我们窗口的时机,我们这里只有当我们的总数量达标之后才可以,那么如果说我们某一个字符在这个窗口内的数量以及达标或者超过需要的数量,比如要2个a,但是窗口内的该字符数量有3个a了,但是如果说我们其他字符还有缺的话,那么我们仍然要往右扩充,指导每个字符都达到大于等于规定数量,也就是debt小于或者等于0时我们就缩小窗口。
那么对于缩小左边界如果该左边界是其他字符,那么我们直接缩小,但是如果是特定字符,那么我们得查询哈希表,看看该字符的数量,如果是负数的话,那么说明超过规定的数量,因为我们右边界有该字符我们都是直接在哈希表对应位置处减减,缩小玩之后,我们再在表中对负数位置记录加一,如果是0,那么在缩小则会小于规定数量,那么只能停止缩小在往右扩,并且每次缩小的是特定字符的话,我们还要将debt变量加一如果debt是负数的话,那么当不能缩小该特定字符并且debt变量为0时记录答案。
代码实现:
class Solution {
public:string minWindow(const std::string& s, const std::unordered_map<char, int>& required) {int debt = 0;for (const auto& pair : required) {debt += pair.second;}int l = 0, r = 0;int minLength = INT_MAX;string result = "";unordered_map<char, int> count = required;while (r < s.size()) {if (count.find(s[r]) != count.end()) {debt--;count[s[r]]--;}while (debt <=0) {if (r - l + 1 < minLength) {minLength = r - l + 1;result = s.substr(l, minLength);}if (count.find(s[l]) != count.end()) {if(count[s[l]]==0){break}count[s[l]]++;if(debt+1>0){break;}debt++;}}l++;}r++;}return result;}
};
3.结语
那么这就是本篇文章关于滑动窗口的一个全部内容,那么滑动窗口的思想其实我们发现和二分有点相似,是寻找满足性质边界的一个答案,那么由于这里的单调性是和我们的窗口的长度有关,所以我们能够通过窗口的长度的扩大与缩小来线性的逼近我们的边界点而不用像二分那样每次取中点那样逼近
那么如果本篇文章让你有所收获,那么我们便感到非常开心,那么我会持续更新,希望你能够多多关注与支持,如果该文章由帮组到你,那么也留下个一键三连来支持一下,你的支持就是我创作的最大动力!

相关文章:

滑动窗口算法篇:连续子区间与子串问题
1.滑动窗口原理 那么一谈到子区间的问题,我们可能会想到我们可以用我们的前缀和来应用子区间问题,但是这里对于子区间乃至子串问题,我们也可以尝试往滑动窗口的思路方向去进行一个尝试,那么说那么半天,滑动窗口是什么…...

Python爬虫实战:股票分时数据抓取与存储 (1)
在金融数据分析中,股票分时数据是投资者和分析师的重要资源。它能够帮助我们了解股票在交易日内的价格波动情况,从而为交易决策提供依据。然而,获取这些数据往往需要借助专业的金融数据平台,其成本较高。幸运的是,通过…...

【设计模式】【行为型模式】访问者模式(Visitor)
👋hi,我不是一名外包公司的员工,也不会偷吃茶水间的零食,我的梦想是能写高端CRUD 🔥 2025本人正在沉淀中… 博客更新速度 👍 欢迎点赞、收藏、关注,跟上我的更新节奏 🎵 当你的天空突…...

基于实例详解pytest钩子pytest_generate_tests动态生成测试的全过程
关注开源优测不迷路 大数据测试过程、策略及挑战 测试框架原理,构建成功的基石 在自动化测试工作之前,你应该知道的10条建议 在自动化测试中,重要的不是工具 作为一名软件开发人员,你一定深知有效测试策略的重要性,尤其…...

Copilot基于企业PPT模板生成演示文稿
关于copilot创建PPT,咱们写过较多文章了: Copilot for PowerPoint通过文件创建PPT Copilot如何将word文稿一键转为PPT Copilot一键将PDF转为PPT,治好了我的精神内耗 测评Copilot和ChatGPT-4o从PDF创建PPT功能 Copilot for PPT全新功能&a…...

2025百度快排技术分析:模拟点击与发包算法的背后原理
一晃做SEO已经15年了,2025年还有人问我如何做百度快速排名,我能给出的答案就是:做好内容的前提下,多刷刷吧!百度的SEO排名算法一直是众多SEO从业者研究的重点,模拟算法、点击算法和发包算法是百度快速排名的…...

七星棋牌全开源修复版源码解析:6端兼容,200种玩法全面支持
本篇文章将详细讲解 七星棋牌修复版源码 的 技术架构、功能实现、二次开发思路、搭建教程 等内容,助您快速掌握该棋牌系统的开发技巧。 1. 七星棋牌源码概述 七星棋牌修复版源码是一款高度自由的 开源棋牌项目,该版本修复了原版中的多个 系统漏洞&#…...

解锁原型模式:Java 中的高效对象创建之道
系列文章目录 后续补充~~~ 文章目录 一、引言1.1 软件开发中的对象创建困境1.2 原型模式的登场 二、原型模式的核心概念2.1 定义与概念2.2 工作原理剖析2.3 与其他创建型模式的差异 三、原型模式的结构与角色3.1 抽象原型角色3.2 具体原型角色3.3 客户端角色3.4 原型管理器角色…...

DeepSeek从入门到精通:揭秘 AI 提示语设计误区与 AI 幻觉(新手避坑指南)
文章目录 引言常见陷阱与应对策略:新手必知的提示词设计误区缺乏迭代陷阱:期待一次性完美结果过度指令与模糊指令陷阱:当细节缺乏重点或意图不明确假设偏见陷阱:当前 AI 只听你想听的幻觉生成陷阱:当AI自信地胡说八道忽…...

Jenkins同一个项目不同分支指定不同JAVA环境
背景 一些系统应用,会为了适配不同的平台,导致不同的分支下用的是不同的gradle,导致需要不同的JAVA环境来编译,比如a分支需要使用JAVA11, b分支使用JAVA17。 但是jenkins上,一般都是Global Tool Configuration 全局所有环境公用一个JAVA_HOME。 尝试过用 Build 的Execut…...
从入门到精通:Postman 实用指南
Postman 是一款超棒的 API 开发工具,能用来测试、调试和管理 API,大大提升开发效率。下面就给大家详细讲讲它的安装、使用方法,再分享些实用技巧。 一、安装 Postman 你能在 Postman 官网(https://www.postman.com )下…...

win32汇编环境,对话框中使用月历控件示例二
;运行效果 ;win32汇编环境,对话框中使用月历控件示例二 ;以下示例有2个操作,即将每周的开始日进行改变,将默认的周日开始改为周一开始,同时实现点击哪个日期,则设定为哪个日期 ;直接抄进RadAsm可编译运行。重要部分加备注。 ;下面为asm文件 ;>>>>>>>&…...
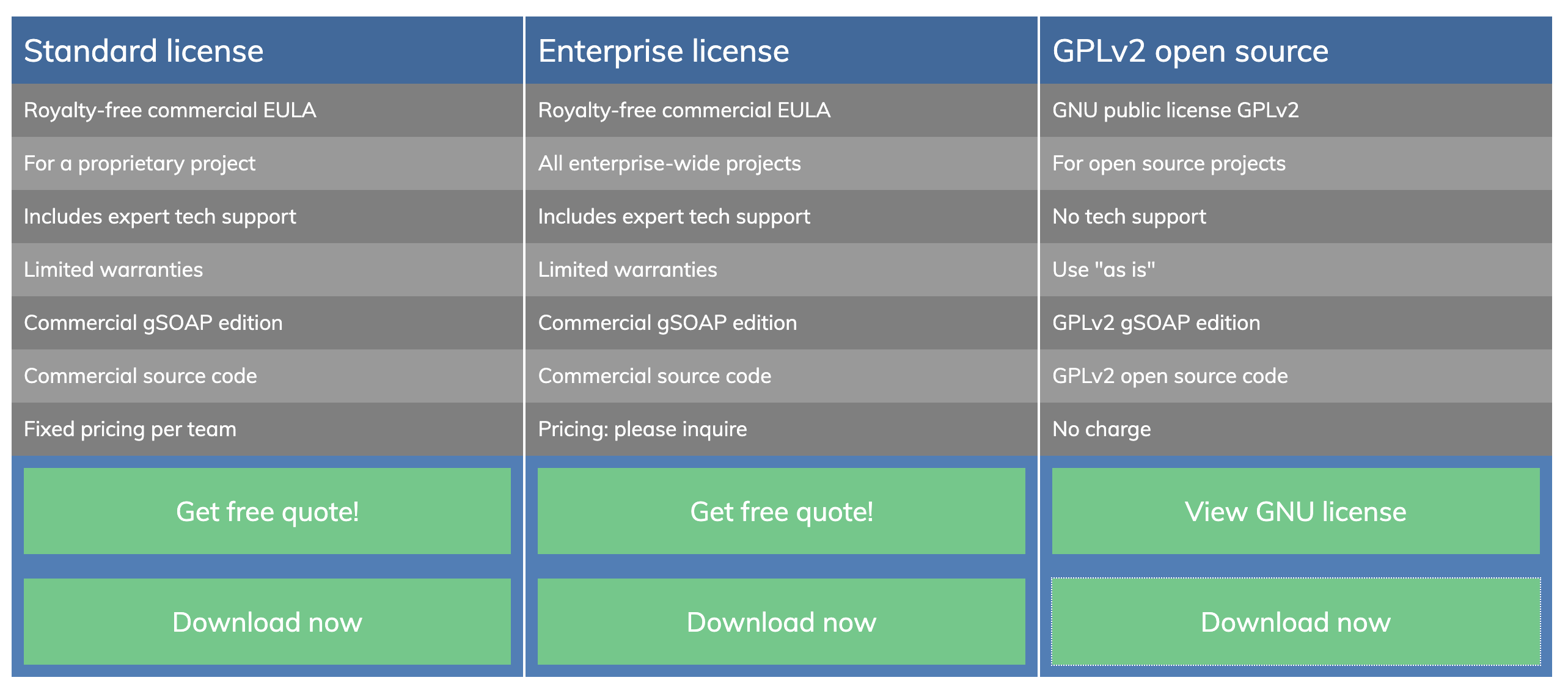
gsoap实现webservice服务
gsoap实现webservice服务 在实现Web服务时,使用gSOAP是一个很好的选择,因为它提供了强大的工具和库来创建SOAP和RESTful服务。gSOAP是一个C和C语言开发的库,它支持SOAP协议的各种版本,包括SOAP 1.1和SOAP 1.2。下面是如何使用gSO…...

容联云联络中心AICC:深度整合DeepSeek,业务验证结果公开
容联云重磅推出AICC3.2版本,实现了智能化的升级与外呼效率的突破——深度整合DeepSeek-R1大模型、预测式外呼在数据分析侧的增强、全渠道路由能力、一键多呼效率的强化。 同时,全面接入DeepSeek-R1的容联云 AICC3.2 ,目前已与某知名汽车金融企…...

腿足机器人之七- 逆运动学
腿足机器人之七- 逆运动学 基本概念腿部运动的数学表示坐标系定义以及自由度说明正运动学模型 逆运动学求解几何解法数值迭代法雅可比矩阵法基础双足机器人步态规划中的雅可比法应用 工程挑战与解决方案实际应用中的工具和算法多解问题高自由度机器人(如Atlas的28自…...

快速点位排查问题的方法
一、核心思路:缩小问题范围 1. 分治法(Divide and Conquer) 原理:将复杂系统拆分为独立模块,逐层验证。示例: 网络问题:检查客户端 → 本地网络 → 服务器 → 数据库。代码问题:注…...

【前端】Vue组件库之Element: 一个现代化的 UI 组件库
文章目录 前言一、官网1、官网主页2、设计原则3、导航4、组件 二、核心功能:开箱即用的组件生态1、丰富的组件体系2、特色功能亮点 三、快速上手:三步开启组件化开发1、安装(使用Vue 3)2、全局引入3、按需导入(推荐&am…...

一文搞懂Android应用元素查看器(Appium+Appium-inspector)——定位微信布局元素
Appium和Appium Inspector是怎么协作的呢?Appium 与 Appium Inspector 的版本匹配Appium安装启动appium服务安装Appium inspector客户端查看安卓真机指定app布局元素(这里以微信为例,需要保持与模拟器或真机一直连接)【QA】解决顶部工具栏上Refresh Source & Screensho…...

matlab质子磁力仪传感器线圈参数绘图
1、内容简介 matlab134-质子磁力仪传感器线圈参数绘图 可以交流、咨询、答疑 2、内容说明 略 线圈是质子磁力仪传感器的核心,其品质直接影响着仪器的测量精度 。 结合反向串联圆柱体线圈模型,对约束设计 的因素进行分析; 建立约束参数与设计参数之间…...

WPF快速创建DeepSeek本地自己的客户端-基础思路版本
开发工具:VS 2015 开发环境:.Net 4.0 使用技术:WPF 本篇文章内容: 本地部署DeepSeek以后一般使用网页工具(如Chatbox)或者DOS窗口与其对话。本篇文章使用WPF创建一个基础版的对话工具。 一、搭建本地DeepS…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...
