2.18寒假
今天在题单中看了搜索。

解析:两个一维数组,用于表示上下左右四个方向的偏移量,分别对应 x 轴和 y 轴的偏移,遍历四个方向(左、右、下、上),对于每个方向,检查目标位置是否未走过(temp[x + dx[i]][y + dy[i]] == 0)且不是障碍(map[x + dx[i]][y + dy[i]] == 1)。如果满足条件,将当前位置标记为已走过(temp[x][y] = 1),然后递归调用 walk 函数继续搜索。递归返回后,将当前位置标记为未走过(temp[x][y] = 0),以便尝试其他可能的路径。首先读取地图的长 n、宽 m 和障碍总数 T。
将地图的所有位置初始化为可通行(map[ix][iy] = 1)。读取起点坐标 (sx, sy) 和终点坐标 (fx, fy)。
循环 T 次,每次读取一个障碍的坐标 (l, r),并将该位置标记为障碍(map[l][r] = 0)。
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int map[6][6];
int temp[6][6];
int dx[4] = {0, 0, 1, -1};
int dy[4] = {-1, 1, 0, 0};
int total, fx, fy, sx, sy, T, n, m, l, r;
void walk(int x, int y) {if (x == fx && y == fy) {total++;return;} else {for (int i = 0; i <= 3; i++) {if (temp[x + dx[i]][y + dy[i]] == 0 && map[x + dx[i]][y + dy[i]] == 1) {temp[x][y] = 1;walk(x + dx[i], y + dy[i]);temp[x][y] = 0;}}}
}
int main() {scanf("%d %d %d", &n, &m, &T);for (int ix = 1; ix <= n; ix++) {for (int iy = 1; iy <= m; iy++) {map[ix][iy] = 1;}}scanf("%d %d", &sx, &sy);scanf("%d %d", &fx, &fy);for (int u = 1; u <= T; u++) {scanf("%d %d", &l, &r);map[l][r] = 0;}walk(sx, sy);printf("%d", total);return 0;
}
解析:将当前位置 (o, p) 标记为 1,表示该位置已经被访问过。循环遍历四个方向(右、下、左、上),递归调用 dfs 函数继续搜索相邻位置。从矩阵的四条边界(上、下、左、右)开始调用 dfs 函数进行搜索。因为边界上的 0 肯定不会被 1 完全包围,通过 DFS 可以将与边界上的 0 相连通的所有 0 标记为 1。遍历 a 数组,如果某个位置的值仍然为 0,说明该位置的 0 被 1 完全包围,将 b 数组中对应位置的值改为 2。
#include<stdio.h>
int a[30][30],b[30][30];
int dx[5]={0,0,1,0,-1};
int dy[5]={0,1,0,-1,0};
int n;
void dfs(int o,int p)
{int i;if(o<0||o>n+1||p<0||p>n+1||a[o][p]!=0){return;}a[o][p]=1;for(i=1;i<=4;i++){dfs(o+dx[i],p+dy[i]);}
}int main()
{int i,j;scanf("%d",&n);for(i=0;i<n;i++){for(j=0;j<n;j++){scanf("%d",&a[i][j]);b[i][j]=a[i][j];}}for(i=0;i<n;i++)dfs(0,i);for(i=0;i<n;i++)dfs(n-1,i);for(i=0;i<n;i++)dfs(i,0);for(i=0;i<n;i++)dfs(i,n-1);for(i=0;i<n;i++){for(j=0;j<n;j++){if(a[i][j]==0)b[i][j]=2;}}for(i=0;i<n;i++){for(j=0;j<n;j++)printf("%d ",b[i][j]);printf("\n");}return 0;
}相关文章:

2.18寒假
今天在题单中看了搜索。 解析:两个一维数组,用于表示上下左右四个方向的偏移量,分别对应 x 轴和 y 轴的偏移,遍历四个方向(左、右、下、上),对于每个方向,检查目标位置是否未走过&am…...
的集成(二))
Docker 与持续集成 / 持续部署(CI/CD)的集成(二)
五、代码示例与解释 (一)Dockerfile 示例 以下是一个简单的基于 Python Flask 应用的 Dockerfile 示例: # 使用Python 3.10-slim作为基础镜像 FROM python:3.10-slim # 设置工作目录 WORKDIR /app # 复制项目文件到容器内的工作目录 C…...
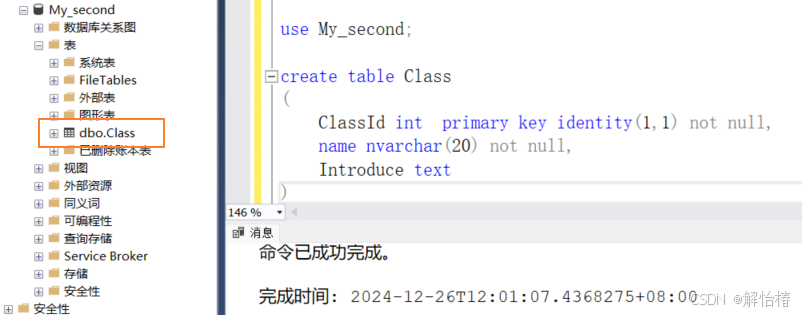
SQL Server的安装和简单使用
目录 一、SQL Server 1.1、简介 1.2、安装包 二、安装SQL Server 2.1、双击安装包 2.2、选择自己想要安装的位置 2.3、点击安装 2.4、安装完成之后会出现以下页面,按照序号依次点击 2.5、不用管密钥,点击下一步 2.6、选择【我接受】 2.7、是否…...
汉诺塔问题)
c/c++蓝桥杯经典编程题100道(19)汉诺塔问题
汉诺塔问题 ->返回c/c蓝桥杯经典编程题100道-目录 目录 汉诺塔问题 一、题型解释 二、例题问题描述 三、C语言实现 解法1:递归法(难度★) 解法2:迭代法(难度★★★) 四、C实现 解法1࿱…...

Linux 信号量
Linux 信号量 一、信号量基础概念1.1 同步机制的核心需求1.2 信号量的核心原理1.3 信号量类型对比 二、实战代码解析2.1 共享内存与信号量结合示例2.2 信号量类实现要点 三、关键实现细节分析3.1 初始化三步骤3.2 SEM_UNDO机制3.3 原子操作保证 四、进阶应用场景4.1 生产者-消费…...

Qt开发①Qt的概念+发展+优点+应用+使用
目录 1. Qt的概念和发展 1.1 Qt的概念 1.2 Qt 的发展史: 1.3 Qt 的版本 2. Qt 的优点和应用 2.1 Qt 的优点: 2.2 Qt 的应用场景 2.3 Qt 的应用案例 3. 搭建 Qt 开发环境 3.1 Qt 的开发工具 3.2 Qt SDK 的下载和安装 3.3 Qt 环境变量配置和使…...

向量库(Vector Database)
向量库 1. 向量库发展史 早期阶段(2000s) 基于关系型数据库的扩展(如 PostgreSQL 的向量插件)。简单相似度计算(如欧氏距离、余弦相似度)。 专用向量库的兴起(2010s) FAISS…...

torchsparse安装过程的问题
1、项目要求torchsparse githttps://github.com/mit-han-lab/torchsparse.gitv1.4.0 2、torch1.8.1cu111 nvcc--version:11.1 这个版本的cuda匹配的gcc、g经常是7.5。设置为7.5. (这个gcc、g版本修改不一定,可以先进行后面的,…...

【核心算法篇七】《DeepSeek异常检测:孤立森林与AutoEncoder对比》
大家好,今天我们来深入探讨一下《DeepSeek异常检测:孤立森林与AutoEncoder对比》这篇技术博客。我们将从核心内容、原理、应用场景等多个方面进行详细解析,力求让大家对这两种异常检测方法有一个全面而深入的理解。 一、引言 在数据科学和机器学习领域,异常检测(Anomaly…...

Win10环境使用零讯ZeroNews内网穿透实现Deepseek对外服务
Win10环境使用零讯ZeroNews内网穿透实现Deepseek对外服务 前言 之前笔者已经在Win10环境搭建好了Ollama、DeepSeek、Open WebUI、Dify等组件,成功实现了私有化部署及内网访问: https://lizhiyong.blog.csdn.net/article/details/145505686 https://l…...

CUDA 安装 一直卡在Installing Nsight Visual Studio Edition
最近在安装CUDA的时候,CUDA 安装 一直卡在Installing Nsight Visual Studio Edition,莫名的一直卡在安装进行中这儿,过很久都没进度,如图 后面重新下载了12.6的进行安装也是如此 无论是local还是network,都是这样。度…...

Softing线上研讨会 | 自研还是购买——用于自动化产品的工业以太网
| 线上研讨会时间:2025年1月27日 16:00~16:30 / 23:00~23:30 基于以太网的通信在工业自动化网络中的重要性日益增加。设备制造商正面临着一大挑战——如何快速、有效且经济地将工业以太网协议集成到其产品中。其中的关键问题包括:是否只需集成单一的工…...

STM32 定时器产生定周期方法
目录 背景 程序 第一步、使能PCLK1外设时钟编辑 第二步、时基单元配置 第三步、配置NVIC(设置定时中断优先级)编辑 第四步、使能溢出中断 第五步、使能定时器 第六步、填写中断处理函数(ISR) 背景 在单片机开发当中&…...

解锁机器学习核心算法 | 支持向量机:机器学习中的分类利刃
一、引言 在机器学习的庞大算法体系中,有十种算法被广泛认为是最具代表性和实用性的,它们犹如机器学习领域的 “十大神器”,各自发挥着独特的作用。这十大算法包括线性回归、逻辑回归、决策树、随机森林、K - 近邻算法、K - 平均算法、支持向…...

青少年编程与数学 02-009 Django 5 Web 编程 21课题、部署
青少年编程与数学 02-009 Django 5 Web 编程 21课题、部署 一、软件开发部署部署的主要内容部署的步骤部署的方式部署的环境 二、Django项目部署1. 准备工作2. 代码部署3. 配置Django项目4. Web服务器和应用服务器配置5. 安全和性能优化6. 监控和日志管理7. 测试和上线 三、在U…...

ARM系统源码编译OpenCV 4.10.0(包含opencv_contrib)
因项目部署在ARM系统上,需要编译一个arm版本的opencv-4.10.0(带opencv_contrib)版本。 若需要Linux系统下源码安装OpenCV,可参考:https://blog.csdn.net/qq_45445740/article/details/142770493?spm1001.2014.3001.55…...

cmake:定位Qt的ui文件
如题。在工程中,将h,cpp,ui文件放置到不同文件夹下,会存在cmake找不到ui文件,导致编译报错情况。 cmake通过指定文件路径,确保工程找到ui文件。 标识1:ui文件保存路径。 标识2:添加…...
1749. 任意子数组和的绝对值的最大值)
(leetcode 1749 前缀和)1749. 任意子数组和的绝对值的最大值
核心题意 任意子数组和 的绝对值的最大值实际上是前缀和之间的差的最大值 建立前缀和数组 如果我们只考虑前缀和的最大值和最小值之差,那么就能够获得一个最大的子数组和的绝对值。因为任意一个子数组的和 prefix[j1] - prefix[i],它的绝对值是最大当…...

下载安装运行测试开源vision-language-action(VLA)模型OpenVLA
1. 安装 项目官网OpenVLA 首先按照官网提示的以下代码,执行创建环境->安装最小依赖->git克隆项目等 # Create and activate conda environment conda create -n openvla python3.10 -y conda activate openvla# Install PyTorch. Below is a sample comma…...

【网络安全 | 漏洞挖掘】我如何通过Cookie Manipulation发现主域上的关键PII?
未经许可,不得转载。 文章目录 正文正文 在分析 Example.com 的认证机制时,我注意到一个特定的 cookie,USER_ID,包含了一个具有预测性的会话标识符,其格式为: USER_ID="VYCVCDs-TZBI:XXXX-random-data"其中,XXXX 是由四个大写字母组成的部分,我使用 Burp S…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
