每日一题——编辑距离
编辑距离
- 参考资料
- 题目描述
- 示例
- 解题思路
- 动态规划(DP)方法
- 代码实现
- 复杂度分析
- 示例详解
- 示例1:`"nowcoder"` → `"new"`
- 示例2:`"intention"` → `"execution"`
- 总结与心得
参考资料
建议先参考下面一个视频和文档,然后再思考问题,不然很容易会被吓到。
——
https://programmercarl.com/0072.%E7%BC%96%E8%BE%91%E8%B7%9D%E7%A6%BB.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE

题目描述
给定两个字符串 str1 和 str2,计算将 str1 转换为 str2 所需的最小操作次数。每次操作可以执行以下三种操作之一:
- 插入一个字符
- 删除一个字符
- 修改一个字符
示例
- 示例1:
- 输入:
"nowcoder", "new" - 输出:
6 - 解释:修改 ‘o’ 为 ‘e’,删除后续5个字符
- 输入:
- 示例2:
- 输入:
"intention", "execution" - 输出:
5 - 解释:需要修改前5个字符
- 输入:
解题思路
动态规划(DP)方法
-
状态定义
dp[i][j]表示将str1的前i个字符转换为str2的前j个字符所需的最小操作次数
-
状态转移方程
- 当
str1[i-1] == str2[j-1]时:dp[i][j] = dp[i-1][j-1] - 否则,取三种操作的最小值加1:
- 修改操作:
dp[i-1][j-1] + 1 - 插入操作:
dp[i][j-1] + 1 - 删除操作:
dp[i-1][j] + 1
- 修改操作:
- 当
-
初始化
dp[i][0] = i:表示删除操作dp[0][j] = j:表示插入操作
代码实现
#include <string.h> // 引入字符串处理函数库,用于调用strlen等函数// 辅助函数:计算三个整数中的最小值
int min(int a, int b, int c) {// 使用三元运算符实现最小值计算// 首先比较a和b,取较小值,再与c比较,最终返回最小值return a < b ? (a < c ? a : c) : (b < c ? b : c);
}// 主函数:计算两个字符串之间的编辑距离
int editDistance(char* str1, char* str2) {// 获取两个字符串的长度int len1 = strlen(str1); // str1的长度int len2 = strlen(str2); // str2的长度// 处理空字符串情况// 如果str1为空,将str2的所有字符插入到str1中,需要len2次操作if (len1 == 0) return len2;// 如果str2为空,将str1的所有字符删除,需要len1次操作if (len2 == 0) return len1;// 创建动态规划表dp,大小为(len1+1)×(len2+1)// dp[i][j]表示str1的前i个字符转换为str2的前j个字符所需的最小操作数int dp[len1 + 1][len2 + 1];// 初始化动态规划表的第一行和第一列// dp[i][0]:将str1的前i个字符转换为空字符串,需要i次删除操作for (int i = 0; i <= len1; i++) dp[i][0] = i;// dp[0][j]:将空字符串转换为str2的前j个字符,需要j次插入操作for (int j = 0; j <= len2; j++) dp[0][j] = j;// 动态规划过程:填充dp表// 遍历str1和str2的每个字符for (int i = 1; i <= len1; i++) {for (int j = 1; j <= len2; j++) {// 如果当前字符相同,不需要额外操作,直接继承左上角的值if (str1[i - 1] == str2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];} else {// 如果当前字符不同,选择三种操作的最小值 + 1// dp[i - 1][j - 1]:替换操作// dp[i][j - 1]:插入操作// dp[i - 1][j]:删除操作dp[i][j] = min(dp[i - 1][j - 1], dp[i][j - 1], dp[i - 1][j]) + 1;}}}// 返回最终的编辑距离,即dp表右下角的值return dp[len1][len2];
}
复杂度分析
- 时间复杂度:O(mn),其中m和n分别是两个字符串的长度
- 空间复杂度:O(mn),需要一个二维数组存储动态规划的状态
示例详解
示例1:"nowcoder" → "new"
- 对于第一个位置,两个字符串都是’n’,不需要操作
- 第二个位置,需要将’o’修改为’e’,操作数+1
- 接下来需要删除"wcoder"这5个字符,每个字符删除操作数+1
- 最终需要6次操作
示例2:"intention" → "execution"
- 两个字符串后缀"tion"相同,不需要操作
- 需要修改前5个字符,每个字符修改操作数+1
- 最终需要5次操作
总结与心得
这道题虽然看起来操作较多(增删改),但实际难度适中,比起IP地址字符串转换的题目要简单一些。关键在于理解动态规划的状态设计:
-
一开始可能会想直接用m×n的dp数组(去掉第一行第一列),但这样是不行的。因为如果两个字符串完全相同,结果应该是0,所以需要包含这种情况。
-
初始化很重要:第一行和第一列分别表示纯粹的删除和插入操作,这为后续的状态转移奠定了基础。
-
状态转移方程的设计体现了问题的本质:当字符相同时不需要操作,当字符不同时取三种操作的最小值。
相关文章:

每日一题——编辑距离
编辑距离 参考资料题目描述示例 解题思路动态规划(DP)方法 代码实现复杂度分析示例详解示例1:"nowcoder" → "new"示例2:"intention" → "execution" 总结与心得 参考资料 建议先参考下…...

TensorFlow项目GPU运行 安装步骤
以下是在 Linux 系统 下搭建完整 GPU 加速环境的详细流程(适配 CUDA 11.2 和 Python 3.9): 1. 前置检查 1.1 验证 NVIDIA 驱动 # 检查驱动版本(需 ≥ 450.80.02) nvidia-smi 输出示例: CUDA Version: 11.2…...

c++进阶———继承
1.引言 在一些大的项目中,我们可能要重复定义一些类,但是很麻烦,应该怎么办呢?举个简单的例子,我要做一个全校师生统计表,统计学号,教师编号,姓名,年龄,电话…...

FreeSwitch的mod_translate模块详细,附带场景案例及代码示例
mod_translate 模块详细介绍 mod_translate 是 FreeSWITCH 中的一个拨号计划应用程序模块,用于对电话号码或字符串进行格式转换和翻译。它可以根据预定义的规则对输入的内容进行匹配和转换,常用于号码格式化、路由选择、号码屏蔽等场景。 主要功能 号码…...

前端504错误分析
前端出现504错误(网关超时)通常是由于代理服务器未能及时从上游服务获取响应。以下是详细分析步骤和解决方案: 1. 确认错误来源 504含义:代理服务器(如Nginx、Apache)在等待后端服务响应时超时。常见架构:前端 → 代理服务器 → 后端服务,问题通常出在代理与后端之间。…...

在 .NET 8/9 中使用 AppUser 进行 JWT 令牌身份验证
文章目录 一、引言二、什么是 JSON Web 令牌?三、什么是 JSON Web 令牌结构?四、设置 JWT 令牌身份验证4.1 创建新的 .NET 8 Web API 项目4.2 安装所需的 NuGet 软件包4.3 创建 JWT 配置模型4.4 将 JWT 配置添加到您的 appsettings.json 中4.5 为 Config…...

基于python实现机器学习的心脏病预测系统
以下是一个基于 Python 实现的简单心脏病预测系统代码示例,我们将使用 Scikit - learn 库中的机器学习算法(这里以逻辑回归为例),并使用公开的心脏病数据集。 步骤: 数据加载与预处理:加载心脏病数据集&a…...

使用 NVM 随意切换 Node.js 版本
安装nvm https://github.com/coreybutler/nvm-windows/releases nvm安装详细教程(卸载旧的nodejs,安装nvm、node、npm、cnpm、yarn及环境变量配置)-CSDN博客 验证 NVM 是否安装成功-查看版本 nvm --version安装指定版本的 Node.js nvm i…...

【Prometheus】prometheus结合pushgateway实现脚本运行状态监控
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,阿里云开发者社区专家博主,CSDN全栈领域优质创作者,掘金优秀博主,51CTO博客专家等。 🏆《博客》:Python全…...

SpringBoot 项目配置动态数据源
目录 一、前言二、操作1、引入依赖2、配置默认数据库 13、定义数据源实体和 Repository4、定义动态数据源5、配置数据源6、定义切换数据源注解7、定义切面类8、使用注解切换数据源 一、前言 通过切面注解方式根据不同业务动态切换数据库 二、操作 1、引入依赖 <dependen…...

CSS基本选择器
1. 通配选择器 作用:可以选中所有的 HTML 元素。 语法: * { 属性名: 属性值; } 举例: <!DOCTYPE html> <html lang"zh-cn"> <head><meta charset"UTF-8"><meta name"viewport" …...

idea-代码补全快捷键
文章目录 前言idea-代码补全快捷键1. 基本补全2. 类型匹配补全3. 后缀补全4. 代码补全 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易啊^ _ ^。 而且听说点赞的人每天的运气都不会太差,…...

基于SpringBoot+vue粮油商城小程序系统
粮油商城小程序为用户提供方便快捷的在线购物体验,包括大米、面粉、食用油、调味品等各种粮油产品的选购,用户可以浏览商品详情、对比价格、下单支付等操作。同时,商城还提供优惠活动、积分兑换等福利,让用户享受到更多实惠和便利…...

挪车小程序挪车二维码php+uniapp
一款基于FastAdminThinkPHP开发的匿名通知车主挪车微信小程序,采用匿名通话的方式,用户只能在有效期内拨打车主电话,过期失效,从而保护车主和用户隐私。提供微信小程序端和服务端源码,支持私有化部署。 更新日志 V1.0…...

企业内部知识库:安全协作打造企业智慧运营基石
内容概要 作为企业智慧运营的核心载体,企业内部知识库通过结构化的信息聚合与动态化的知识流动,为组织提供了从数据沉淀到价值转化的系统性框架。其底层架构以权限管理为核心,依托数据加密技术构建多层级访问控制机制,确保敏感信…...

网络安全推荐的视频教程 网络安全系列
第一章 网络安全概述 1.2.1 网络安全概念P4 网络安全是指网络系统的硬件、软件及其系统中的数据受到保护,不因偶然的或恶意的原因而遭到破坏、更改、泄露,系统连续可靠正常地运行,网络服务不中断。 1.2.3 网络安全的种类P5 (1…...
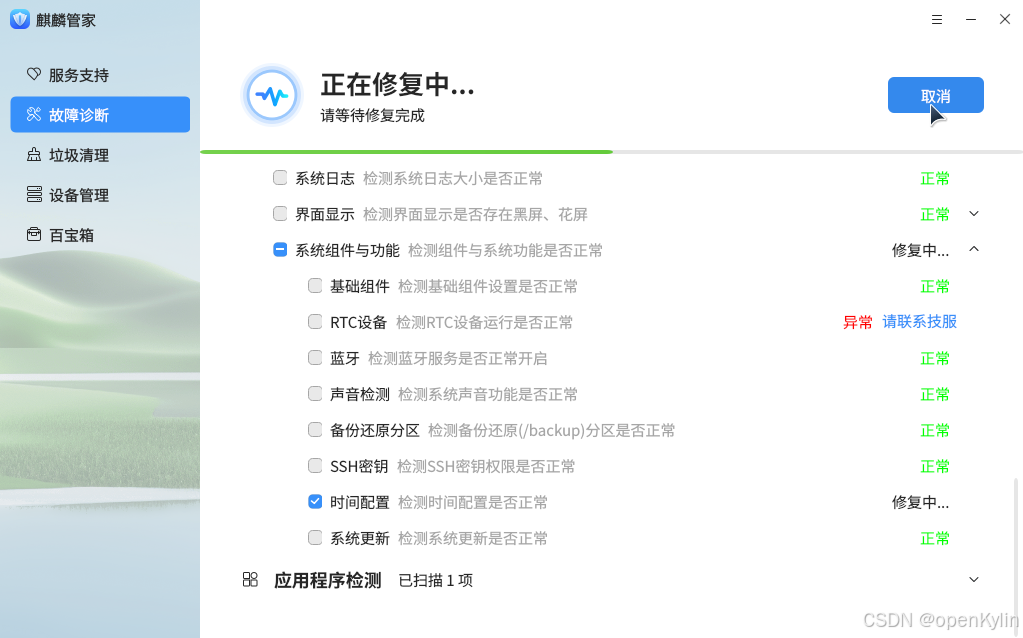
麒麟管家全新升级,运维问题“一键修复”
麒麟管家是openKylin社区SystemManager SIG开发的一款面向社区用户,能倾听用户烦恼和诉求,也能提供便利途径、解决用户问题的系统管理类应用,可以为用户提供问题反馈、系统垃圾清理、电脑故障排查、硬件设备管理及系统小工具等一站式服务&…...
机制讲解)
MVCC(多版本并发控制)机制讲解
MVCC(Multi-Version Concurrency Control,多版本并发控制)这是一个在数据库管理系统中非常重要的技术,尤其是在处理并发事务时。别担心,我会用简单易懂的方式来讲解,让你轻松掌握它的原理和作用。 1. 什么是…...

React 与 Vue 对比指南 - 上
React 与 Vue 对比指南 - 上 本文将展示如何在 React 和 Vue 中实现常见功能,从基础渲染到高级状态管理 Hello 分别使用 react 和 vue 写一个 Hello World! react export default () > {return <div>Hello World!</div>; }vue <…...

开源协议深度解析:理解MIT、GPL、Apache等常见许可证
目录 前言1. MIT协议:自由而宽松的开源许可1.1 MIT协议的主要特点1.2 MIT协议的适用场景 2. GPL协议:自由软件的捍卫者2.1 GPL协议的核心理念2.2 GPL协议的适用场景 3. Apache License 2.0:开源与专利保护的平衡3.1 Apache License 2.0的主要…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
