LeetCode 热题 100_寻找两个正序数组的中位数(68_4_困难_C++)(二分查找)(先合并再挑选中位数;划分数组(二分查找))
LeetCode 热题 100_寻找两个正序数组的中位数(68_4)
- 题目描述:
- 输入输出样例:
- 题解:
- 解题思路:
- 思路一(先合并再挑选中位数):
- 思路二(划分数组(二分查找)):
- 代码实现
- 代码实现(思路一(先合并再挑选中位数)):
- 代码实现(思路二(划分数组(二分查找))):
- 以思路二为例进行调试
题目描述:
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
输入输出样例:
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
nums1.length== m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106
题解:
解题思路:
思路一(先合并再挑选中位数):
1、因两个数组是有序,可以通过两个指针将两个数组进行合并,在进行合并时每次挑选一个较小的元素进行合并。合并后再挑选中位数,如果合并后元素个数为奇数,则返回中间的元素。如果为偶数则返回中间两个元素的平均数。
2、复杂度分析:
① 时间复杂度:O(m+n),m和n分别为两个有序数组元素的个数。合并两个有序数组的时间复杂度为O(m+n)。查找合并后的中位数时间为O(1)。
② 空间复杂度:O(m+n),需要一个额外的数组来存储合并后的数组。
思路二(划分数组(二分查找)):
1、我们首先考虑一个有序数组取中位数的情况:nums=[2,3,4,6,8,9,10,12,18,20] , n=10。
我们可以将分隔线放在8和9之间:[2,3,4,6,8 | 9 ,10,12,18,20]。(当元素个数为奇数时,左侧元素多1)
将nums拆分成两个数组(分隔线的情况如下):
nums1=[3,8 | 9,10]
nums2=[2,4,6 | 12,18,20]
将nums拆分成两个数组(分隔线的情况如下):
nums1=[2,3,4 |]
nums2=[6,8 | 9,10,12,18,20]
发现其中的规律:
① 分隔线的左侧元素值小于右侧元素值,且当前数组右侧的元素值大于另一个数组左侧的元素值。
② 分隔线左侧的元素个数(两个数组)等于分隔线右侧的元素个数或者左侧比右侧多一个元素。
③ 中位数一定在分隔线的左右两侧元素中选取。
2、通过分析出的规律可得出解题的步骤如下:
① 确定 nums1 中的分隔线(二分查找),再通过分隔线左右两侧元素的个数关系,确定 nums2 中的分隔线。
② 确定分隔线后,若nums1中左侧元素 > nums2中的右侧元素,则nums1中的分隔线需左移减小nums1中左侧元素的值(这里和下方的左侧元素和右侧元素指的是分隔线相邻的元素)。
③ 确定分隔线后,若nums2中左侧元素 > nums1中的右侧元素,则nums1中的分隔线需右移,增大nums1中右侧元素的值。
④ 确定分隔线后,若nums1中左侧元素 <= nums2中的右侧元素,且nums2中左侧元素 <= nums1中的右侧元素。若两个数组元素总和为奇数则输出左侧元素的最大值(nums1和nums2分隔线左侧)。若两个数组元素总和为偶数则输出左侧元素的最大值(nums1和nums2分隔线左侧)+右侧元素的最小值 再除以 2。
官方的视频题解链接(挺不错的)
3、复杂度分析
① 时间复杂度:O(logmin(m,n))),其中 m 和 n 分别是数组 nums1和 nums2 的长度,只对其中较小的数组进行二分查找。
② 空间复杂度:O(1)。
代码实现
代码实现(思路一(先合并再挑选中位数)):
class Solution1 {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {// 初始化指针 i, j 用于遍历 nums1 和 nums2,k 用于遍历合并后的数组 mergeint i = 0, j = 0, k = 0;// 创建一个合并后的数组 merge,其大小为 nums1 和 nums2 长度之和vector<int> merge(nums1.size() + nums2.size());// 合并两个已排序的数组 nums1 和 nums2 到 merge 数组中while (i < nums1.size() && j < nums2.size()) {// 比较 nums1 和 nums2 中当前元素的大小,选择较小的元素放入 merge 数组if (nums1[i] <= nums2[j]) {merge[k++] = nums1[i++]; // 将 nums1 的当前元素放入 merge 中} else {merge[k++] = nums2[j++]; // 将 nums2 的当前元素放入 merge 中}}// 如果 nums1 中还有剩余的元素,继续加入 merge 数组while (i < nums1.size()) {merge[k++] = nums1[i++];}// 如果 nums2 中还有剩余的元素,继续加入 merge 数组while (j < nums2.size()) {merge[k++] = nums2[j++];}// 计算合并后数组的中位数索引int mid = (nums1.size() + nums2.size()) / 2;// 如果合并后的数组长度为奇数,中位数就是中间的那个元素if ((nums1.size() + nums2.size()) % 2 == 1) {return double(merge[mid]); // 返回 merge[mid],直接返回该值} else {// 如果合并后的数组长度为偶数,中位数是中间两个数的平均值return double(merge[mid - 1] + merge[mid]) / 2; // 计算并返回平均值} }
};
代码实现(思路二(划分数组(二分查找))):
class Solution2 {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {// 确保 nums1 是较小的数组,以减少二分查找的次数if (nums1.size() > nums2.size()) {return findMedianSortedArrays(nums2, nums1);}int m = nums1.size(); // nums1 的大小int n = nums2.size(); // nums2 的大小int left = 0, right = m; // 在 nums1 数组上进行二分查找的左、右边界// 使用二分查找在较小的数组 nums1 中查找合适的分区while (left <= right) {// 计算 nums1 的分区点int partition1 = (left + right) / 2;// 计算 nums2 的分区点,使得左右两部分元素数量相等或相差1int partition2 = (m + n + 1) / 2 - partition1;// 计算分区后的左右部分的最大值和最小值// nums1 左侧最大值int maxLeft1 = (partition1 == 0) ? INT_MIN : nums1[partition1 - 1];// nums1 右侧最小值int minRight1 = (partition1 == m) ? INT_MAX : nums1[partition1];// nums2 左侧最大值int maxLeft2 = (partition2 == 0) ? INT_MIN : nums2[partition2 - 1];// nums2 右侧最小值int minRight2 = (partition2 == n) ? INT_MAX : nums2[partition2];// 判断分区是否有效if (maxLeft1 <= minRight2 && maxLeft2 <= minRight1) {// 有效分区,计算中位数if ((m + n) % 2 == 0) {// 如果总元素个数是偶数,中位数为左右最大值和最小值的平均值return (max(maxLeft1, maxLeft2) + min(minRight1, minRight2)) / 2.0;} else {// 如果总元素个数是奇数,中位数为左侧的最大值return max(maxLeft1, maxLeft2);}} // 如果 maxLeft1 > minRight2,说明 partition1 太大,需要向左缩小else if (maxLeft1 > minRight2) {right = partition1 - 1; // 调整右边界} // 如果 maxLeft2 > minRight1,说明 partition1 太小,需要向右扩大else {left = partition1 + 1; // 调整左边界}}// 如果没有找到合适的中位数,代码逻辑应达到这里,可能代表输入不符合条件return 0.0; // 通过编译需要添加返回值}
};
以思路二为例进行调试
#include<iostream>
#include <vector>
#include <algorithm>
using namespace std;class Solution2 {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {// 确保 nums1 是较小的数组,以减少二分查找的次数if (nums1.size() > nums2.size()) {return findMedianSortedArrays(nums2, nums1);}int m = nums1.size(); // nums1 的大小int n = nums2.size(); // nums2 的大小int left = 0, right = m; // 在 nums1 数组上进行二分查找的左、右边界// 使用二分查找在较小的数组 nums1 中查找合适的分区while (left <= right) {// 计算 nums1 的分区点int partition1 = (left + right) / 2;// 计算 nums2 的分区点,使得左右两部分元素数量相等或相差1int partition2 = (m + n + 1) / 2 - partition1;// 计算分区后的左右部分的最大值和最小值// nums1 左侧最大值int maxLeft1 = (partition1 == 0) ? INT_MIN : nums1[partition1 - 1];// nums1 右侧最小值int minRight1 = (partition1 == m) ? INT_MAX : nums1[partition1];// nums2 左侧最大值int maxLeft2 = (partition2 == 0) ? INT_MIN : nums2[partition2 - 1];// nums2 右侧最小值int minRight2 = (partition2 == n) ? INT_MAX : nums2[partition2];// 判断分区是否有效if (maxLeft1 <= minRight2 && maxLeft2 <= minRight1) {// 有效分区,计算中位数if ((m + n) % 2 == 0) {// 如果总元素个数是偶数,中位数为左右最大值和最小值的平均值return (max(maxLeft1, maxLeft2) + min(minRight1, minRight2)) / 2.0;} else {// 如果总元素个数是奇数,中位数为左侧的最大值return max(maxLeft1, maxLeft2);}} // 如果 maxLeft1 > minRight2,说明 partition1 太大,需要向左缩小else if (maxLeft1 > minRight2) {right = partition1 - 1; // 调整右边界} // 如果 maxLeft2 > minRight1,说明 partition1 太小,需要向右扩大else {left = partition1 + 1; // 调整左边界}}// 如果没有找到合适的中位数,代码逻辑应达到这里,可能代表输入不符合条件return 0.0; // 通过编译需要添加返回值}
};int main(int argc, char const *argv[])
{vector<int> nums1={1,2};vector<int> nums2={3,4};Solution2 s2;cout<<s2.findMedianSortedArrays(nums1,nums2);return 0;
}
寻找两个正序数组的中位数(68_4)原题链接
欢迎大家和我沟通交流(✿◠‿◠)
相关文章:
(二分查找)(先合并再挑选中位数;划分数组(二分查找)))
LeetCode 热题 100_寻找两个正序数组的中位数(68_4_困难_C++)(二分查找)(先合并再挑选中位数;划分数组(二分查找))
LeetCode 热题 100_寻找两个正序数组的中位数(68_4) 题目描述:输入输出样例:题解:解题思路:思路一(先合并再挑选中位数):思路二(划分数组(二分查找…...

Java多线程与高并发专题——深入ReentrantReadWriteLock
深入ReentrantReadWriteLock 读写锁出现原因 synchronized和ReentrantLock都是互斥锁。如果说有一个操作是读多写少的,还要保证线程安全的话。如果采用上述的两种互斥锁,效率方面很定是很低的。在这种情况下,咱们就可以使用ReentrantReadWr…...

【Python 语法】算法合集
查找二分查找代码大 O 表示法 广度优先搜索代码 狄克斯特拉算法 递归递归调用栈 分而治之(divide and conquer,D&C)贪心教室调度问题背包问题集合覆盖问题 动态规划背包问题旅游行程最优化 遇到问题时, 如果不确定该如何 高效…...

[STM32]从零开始的STM32 BSRR、BRR、ODR寄存器讲解
一、前言 学习STM32一阵子以后,相信大家对STM32 GPIO的控制也有一定的了解了。之前在STM32 LED的教程中也教了大家如何使用寄存器以及库函数控制STM32的引脚从而点亮一个LED,之前的寄存器只是作为一个引入,并没有深层次的讲解,在教…...

C++ ++++++++++
初始C 注释 变量 常量 关键字 标识符命名规则 数据类型 C规定在创建一个变量或者常量时,必须要指定出相应的数据类型,否则无法给变量分配内存 整型 sizeof关键字 浮点型(实型) 有效位数保留七位,带小数点。 这个是保…...

C# 牵手DeepSeek:打造本地AI超能力
一、引言 在人工智能飞速发展的当下,大语言模型如 DeepSeek 正掀起新一轮的技术变革浪潮,为自然语言处理领域带来了诸多创新应用。随着数据隐私和安全意识的提升,以及对模型部署灵活性的追求,本地部署 DeepSeek 成为众多开发者和…...

phpstudy安装教程dvwa靶场搭建教程
GitHub - digininja/DVWA: Damn Vulnerable Web Application (DVWA) Dvwa下载地址 Windows版phpstudy下载 - 小皮面板(phpstudy) 小皮下载地址 1选择windows 版本,点击立即下载 下载完成,进行解压,注意不要有中文路径 点击.exe文件进行安装…...

最新版本SpringAI接入DeepSeek大模型,并集成Mybatis
当时集成这个环境依赖冲突,搞了好久,分享一下依赖配置 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instan…...

FastAPI 学习笔记
简介: FastAPI 是一个用于构建 API 的现代、快速(高性能)的 web 框架,使用 Python 并基于标准的 Python 类型提示。 关键特性: 快速:可与 NodeJS 和 Go 并肩的极高性能(归功于 Starlette 和 Pydantic&…...

Elasticsearch:过滤 HNSW 搜索,快速模式
作者:来自 Elastic Benjamin Trent 通过我们的 ACORN-1 算法实现,探索我们对 Apache Lucene 中的 HNSW 向量搜索所做的改进。 多年来,Apache Lucene 和 Elasticsearch 一直支持使用 kNN 查询的过滤搜索,允许用户检索符合指定元数据…...

华为hcia——Datacom实验指南——STP工作基本原理及STP/RSTP基本功能配置
什么时候需要用到STP 在二层交换网络中,为了避免环路产生。 什么是STP STP生成树协议,是用来在冗余链路上消除二层环路。在众多交换机中,需要设置出一个根桥,其余的交换机称为非根桥,根桥是整个交换网络的核心&…...

Vue核心知识:动态路由实现完整方案
在Vue中实现动态路由,并结合后端接口和数据库表设计,是一个复杂的项目,需要多个技术栈和步骤的配合。以下将详细描述整个实现过程,包括数据库设计、后端接口设计、前端路由配置以及如何实现动态路由的功能。 目录 一、需求分析二…...

【Maui】系统找不到指定的文件Xamarin.Android.Aapt2.targets
文章目录 前言一、问题描述二、解决方案三、软件开发(源码)四、项目展示 前言 .NET 多平台应用 UI (.NET MAUI) 是一个跨平台框架,用于使用 C# 和 XAML 创建本机移动和桌面应用。 使用 .NET MAUI,可从单个共享代码库开发可在 And…...

通过返回的key值匹配字典中的value值
需求 页面中上面搜索项有获取字典枚举接口,table表格中也有根据key匹配字典中的value 方案一 需要做到的要求 这里上面下拉列表是一个组件获取的字典,下面也是通过字典匹配,所以尽量统一封装一个函数,每个组件保证最少变动tabl…...

【Linux第一弹】Linux基础指令(上)
目录 1.ls指令 1.1 ls使用实例 2.pwd指令 3.cd指令 3.1 cd使用实例 4.touch指令 4.1touch使用实例 5.mkdir指令 5.1mkdir使用实例 6.rmdir指令和rm指令 6.1 rmdir指令使用实例->: 6.2 rm指令使用实例 7.man指令 8.cp指令 8.1 cp 使用实例 9.mv指令 9.1mv使用…...

GitCode 助力 JeeSite:开启企业级快速开发新篇章
项目仓库(点击阅读原文链接可直达前端仓库) https://gitcode.com/thinkgem/jeesite 企业级快速开发的得力助手:JeeSite 快速开发平台 JeeSite 不仅仅是一个普通的后台开发框架,而是一套全面的企业级快速开发解决方案。后端基于 …...
CUDA 图像去噪函数fastNlMeansDenoising())
OpenCV计算摄影学(3)CUDA 图像去噪函数fastNlMeansDenoising()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 使用非局部均值去噪算法(Non-local Means Denoising algorithm)执行图像去噪,该算法来源于 http://www.ipol.…...

【react】快速上手基础教程
目录 一、React 简介 1.什么是 React 2.React 核心特性 二、环境搭建 1. 创建 React 项目 2.关键配置 三、核心概念 1. JSX 语法 表达式嵌入 样式处理 2. 组件 (Component) 3. 状态 (State) 与属性 (Props) 4. 事件处理 合成事件(SyntheticEvent) 5. …...

leaflet扩展插件esri-leaflet.js
esri-leaflet.js是一个开源的JavaScript库,它允许开发者在Leaflet地图上轻松地使用Esri的服务,如ArcGIS Online和ArcGIS Server的图层。以下是对esri-leaflet.js插件的详细介绍: 一、主要功能 esri-leaflet.js的主要功能是将Esri的地图服务…...

electron-builder打包时github包下载失败【解决办法】
各位朋友们,在使用electron开发时,选择了electron-builder作为编译打包工具时,是否经常遇到无法从github上下载依赖包问题,如下报错: Get "https://github.com/electron/electron/releases/download/v6.1.12/ele…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
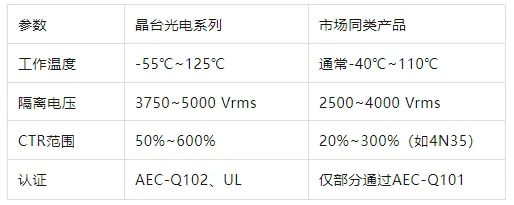
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...
