四类(七种)排序算法总结
一、插入排序
基本思想:
每次将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。即边插入边排序,保证子序列中随时都是排好序的。
基本操作——有序插入:
- 在有序序列中插入一个元素,保持序列有序,有序长度不断增加;
- 起初,a[0]a[0]a[0]是长度为1的子序列。然后,逐一将a[1]a[1]a[1]至a[n−1]a[n-1]a[n−1]插入到有序子序列中。
基本操作——有序插入方法
- 在插入a[i]a[i]a[i]前,数组a的前半段(a[0]a[0]a[0]~a[i−1]a[i-1]a[i−1])是有序段,后半段(a[i]a[i]a[i]~a[n−1]a[n-1]a[n−1])是停留于输入次序的无序段;
- 插入a[i]a[i]a[i]使a[0]a[0]a[0]~a[i]a[i]a[i]有序,也就是要为a[i]a[i]a[i]找到有序位置jjj(0⩽j⩽i0 \leqslant j \leqslant i0⩽j⩽i),将a[i]a[i]a[i]插入在a[j]a[j]a[j]的位置上。
1. 直接插入排序
基本思想:
采用顺序查找法查找插入位置;
性能分析:
算法的时间复杂度为O(n2)O(n^2)O(n2),空间复杂度O(1)O(1)O(1);
稳定性:
稳定。
#include <iostream>
#include <vector>
using namespace std;/*
* @brief: 直接插入排序
* @param v: 待排序序列引用
*/
void insertSort(vector<int>& v)
{int temp; // 辅助空间:用于记录每次要插入的元素值for (int i = 1; i < v.size(); i++) // 认定v[0]已经有序,所以i从1开始{temp = v[i];int j;for (j = i - 1; j >= 0; j--) // 在[0, i-1]中找temp应该插入的位置{if (v[j] > temp){v[j + 1] = v[j]; // 记录后移一位}else // 说明v[0...j]的值都比temp小,无需再比{break;}}v[j + 1] = temp; // j+1就是temp要插入的位置 }
}/*
* @brief: 打印元素
* @param v: 待排序序列引用
*/
void printVec(vector<int>& v)
{for (size_t i = 0; i < v.size(); i++){cout << v[i] << "\t";}cout << endl;
}int main(int argc, char* argv[])
{vector<int> v = { 0,5,3,4,6,2 };cout << "排序前:" << endl;printVec(v);// 排序insertSort(v);cout << "排序后:" << endl;printVec(v);
}

2. 二分插入排序
基本思想:
采用折半查找法查找插入位置;
性能分析:
算法的时间复杂度为O(n2)O(n^2)O(n2),空间复杂度O(1)O(1)O(1);
稳定性:
稳定。
#include <iostream>
#include <vector>
#include <assert.h>
using namespace std;/*
* @brief: 二分插入排序
* @param v: 待排序序列引用
*/
void BinsertSort(vector<int>& v)
{int temp; // 辅助空间:用于记录每次要插入的元素值for (int i = 1; i < v.size(); i++) // 认定v[0]已经有序,所以i从1开始{temp = v[i];// 利用二分法在[0, i-1]中找temp应该插入的位置int low = 0, high = i - 1;while (low <= high){ int mid = (low + high) / 2;if (v[mid] > temp){high = mid - 1;}else{low = mid + 1;}} // low就是该插入的位置// 将[low, i-1]处的元素依次向后移动一位for (int j = i - 1; j >= low; j--){v[j + 1] = v[j];}v[low] = temp; // low就是temp要插入的位置 }
}/*
* @brief: 打印元素
* @param v: 待排序序列引用
*/
void printVec(vector<int>& v)
{for (size_t i = 0; i < v.size(); i++){cout << v[i] << "\t";}cout << endl;
}int main(int argc, char* argv[])
{vector<int> v = { 81,94,11,96,12,35,17,95,28,58,41,75,15 };cout << "排序前:" << endl;printVec(v);// 排序BinsertSort(v);cout << "排序后:" << endl;printVec(v);
}

3. 希尔排序
基本思想:
先将整个待排记录序列分割成若干子序列,分别进行直接插入排序,待整个序列中的记录基本有序时,再对全体记录进行一次直接插入排序;
性能分析:
算法的时间复杂度为O(n1.3)O(n^{1.3})O(n1.3),空间复杂度O(1)O(1)O(1);
稳定性:
不稳定。
特点:
- 缩小增量
- 多遍插入排序
思路:
- 定义增量序列Dk:DM>DM−1>...>D1=1D_{k}:D_{M}>D_{M-1}>...>D_{1}=1Dk:DM>DM−1>...>D1=1
- 对每个DkD_{k}Dk进行“Dk−间隔D_{k}-间隔Dk−间隔”插入排序(k=M, M-1, …1)
特点:
- 一次移动,移动位置较大,跳跃式地接近排序后的最终位置
- 最后一次只需要少量移动
- 增量序列必须时递减的,最后一个必须是1
注:关于 DkD_{k}Dk 如何选择还没有明确定义
#include <iostream>
#include <vector>
using namespace std;/*
* @brief: 希尔排序
* @param v: 待排序序列引用
*/
void ShellSort(vector<int>& v)
{int temp; // 辅助空间int increment = v.size() / 2; // 初始增量while (increment >= 1) // 最后一步的插入排序增量一定是1{for (int i = increment; i < v.size(); i++){temp = v[i];int j;for (j = i - increment; j >= 0; j -= increment){if (v[j] > temp){v[j + increment] = v[j]; // 记录后移increment位}else // 说明v[0...j]的值都比temp小,无需再比{break;}}v[j + increment] = temp; // j+increment就是temp要插入的位置}increment /= 2; // 更新缩小增量}
}/*
* @brief: 打印元素
* @param v: 待排序序列引用
*/
void printVec(vector<int>& v)
{for (size_t i = 0; i < v.size(); i++){cout << v[i] << "\t";}cout << endl;
}int main(int argc, char* argv[])
{vector<int> v = { 81,94,11,96,12,35,17,95,28,58,41,75,15 };cout << "排序前:" << endl;printVec(v);// 排序ShellSort(v);cout << "排序后:" << endl;printVec(v);
}

- 比较希尔排序和直接插入排序的代码发现,二者的相似程度非常高,原因在于希尔排序就是每次以一定的增量 incrementincrementincrement 间隔对序列中的元素进行排序,让序列变得基本有序,当 increment=1increment=1increment=1 时,最后一步就是直接插入排序,由于此刻序列已基本有序,最后一步的排序中需要交换位置的元素已经不多了;
- 速记方法:将直接插入排序代码中的 111 用incrementincrementincrement替换,并在最外层加上以 incrementincrementincrement 为条件的循环。
二、交换排序
基本思想:
两两比较,如果发生逆序则交换,直到所有记录都排好序为止。
1. 冒泡排序
基本思想:
每趟不断将记录两两比较,并按“前小后大”规则交换;
性能分析:
算法的时间复杂度为O(n2)O(n^2)O(n2),空间复杂度O(1)O(1)O(1);
稳定性:
稳定。
#include <iostream>
#include <vector>
using namespace std;/*
* @brief: 冒泡排序
* @param v: 待排序序列引用
*/
void bubbleSort(vector<int>& v)
{int temp; // 辅助空间int n = v.size();for (int i = 1; i < n; i++) // 每次找出一个最大的,n个元素要比较n趟{for (int j = 0; j < n - i; j++){if (v[j] > v[j + 1]) // 比较相邻两个元素大小{// 交换元素temp = v[j];v[j] = v[j + 1];v[j + 1] = temp;}} }
}/**
* @brief: 冒泡排序优化
* @param v: 待排序序列引用
*/
void bubbleSortOpt(vector<int>& v)
{int temp;int n = v.size();bool flag = true; // 记录某一趟中是否交换了元素位置for (int i = 1; i < n && flag; i++){flag = false; // 先将当前趟元素交换标记设为falsefor (int j = 0; j < n - i; j++){if (v[j] > v[j + 1]) // 比较相邻两个元素大小{// 交换元素temp = v[j + 1];v[j + 1] = v[j];v[j] = temp;flag = true; // 发生了元素交换}}}
}/*
* @brief: 打印元素
* @param v: 待排序序列引用
*/
void printVec(vector<int>& v)
{for (size_t i = 0; i < v.size(); i++){cout << v[i] << "\t";}cout << endl;
}int main(int argc, char* argv[])
{vector<int> v = { 81,94,11,96,12,35,17,95,28,58,41,75,15 };cout << "排序前:" << endl;printVec(v);// 排序// bubbleSort(v);bubbleSortOpt(v);cout << "排序后:" << endl;printVec(v);
}

2. 快速排序
基本思想:
- 任取一个元素(如:第一个)为
中心(pivot:枢轴、中心点);- 所有比它小的元素一律前放,比它大的元素一律后放,形成
左右两个子表;- 对各子表重新选择中心元素并依此规则调整(
递归思想);- 直到每个子表的元素只剩一个。
通过一趟排序,将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录进行排序,以达到整个序列有序。
具体实现:
选定一个中间数作为参考,所有元素与之比较,小的调到其左边,大的调到其右边。
每一趟子表的形成是采用从两头向中间交替式逼近法;
由于每趟中对各子表的操作都相似,可采用递归算法。
(枢轴)中间数:
可以是第一个数、最后一个数、最中间一个数、任选一个数等。
性能分析:
算法的时间复杂度为O(nlogn)O(nlogn)O(nlogn),空间复杂度O(logn)O(logn)O(logn)(递归需要使用栈);
稳定性:
不稳定。
#include <iostream>
#include <vector>
using namespace std;/*
* @brief: 快速排序
* @param v: 待排序序列引用
*/
void quickSort(vector<int>& v, int start, int end)
{if (start >= end)return;int low = start, high = end;int pivot = v[low]; // 枢轴while (low < high){while (low < high && v[high] >= pivot) // 将比枢轴小的放到左边high--;v[low] = v[high];while (low < high && v[low] <= pivot) // 将比枢轴大的放到右边low++;v[high] = v[low]; // 将枢轴放置中间某个位置}v[low] = pivot;// 递归左右子表quickSort(v, start, low - 1);quickSort(v, low + 1, end);
}/*
* @brief: 打印元素
* @param v: 待排序序列引用
*/
void printVec(vector<int>& v)
{for (size_t i = 0; i < v.size(); i++){cout << v[i] << "\t";}cout << endl;
}int main(int argc, char* argv[])
{vector<int> v = { 81,94,11,96,12,35,17,95,28,58,41,75,15 };cout << "排序前:" << endl;printVec(v);// 排序quickSort(v, 0, v.size() - 1);cout << "排序后:" << endl;printVec(v);
}

三、选择排序
1. 简单选择排序
基本思想:
在待排序的数据中选出最大(小)的元素放在其最终的位置。
基本操作:
- 首先通过 n−1n-1n−1 次关键字比较,从 nnn 个记录中找出关键字最小的记录,将它与第一个记录交换;
- 再通过 n−2n-2n−2 次比较,从剩余的 n−1n-1n−1 个记录中找出关键字次小的记录,将它与第二个记录交换;
- 重复上述操作,共进行 n−1n-1n−1 趟排序后,排序结束。
性能分析:
算法的时间复杂度为O(n2)O(n^2)O(n2),空间复杂度O(1)O(1)O(1);
稳定性:
不稳定。
#include <iostream>
#include <vector>
using namespace std;/*
* @brief: 选择排序
* @param v: 待排序序列引用
*/
void selectSort(vector<int>& v)
{int temp; // 辅助空间int n = v.size();for (int i = 0; i < n; i++){int minIdx = i;for (int j = minIdx + 1; j < n; j++) // 找出[i...n-1]中最小元素对应index{if (v[j] < v[minIdx]){minIdx = j; // 更新minIdx}}if (minIdx != i){// 交换v[i]和v[minIdx]temp = v[i];v[i] = v[minIdx];v[minIdx] = temp;}}
}/*
* @brief: 打印元素
* @param v: 待排序序列引用
*/
void printVec(vector<int>& v)
{for (size_t i = 0; i < v.size(); i++){cout << v[i] << "\t";}cout << endl;
}int main(int argc, char* argv[])
{vector<int> v = { 81,94,11,96,12,35,17,95,28,58,41,75,15 };cout << "排序前:" << endl;printVec(v);// 排序selectSort(v);cout << "排序后:" << endl;printVec(v);
}

2. 堆排序
堆的定义:
若 nnn 个元素的序列 {a1a_{1}a1, a2a_{2}a2, …, ana_{n}an} 满足
{ai⩽a2iai⩽a2i+1\begin{cases} a_{i} \leqslant a_{2i} \\ a_{i} \leqslant a_{2i+1} \end{cases}{ai⩽a2iai⩽a2i+1 或 {ai⩾a2iai⩾a2i+1\begin{cases} a_{i} \geqslant a_{2i} \\ a_{i} \geqslant a_{2i+1} \end{cases}{ai⩾a2iai⩾a2i+1
则分别称该序列 {a1a_{1}a1, a2a_{2}a2, …, ana_{n}an} 为小根堆和大根堆。
从堆的定义可以看出,堆实质是满足如下性质的完全二叉树:二叉树中任一非叶子节点均小于(大于)它的孩子节点。
堆排序定义:
若在输出堆顶的最小值(最大值)后,使得剩余 n−1n-1n−1 个元素的序列重新又建成一个堆,则得到 nnn 个元素的次小值(次大值)… 如此反复,便能得到一个有序序列,这个过程称之为堆排序。
实现堆排序需解决两个问题:
- 如何由一个无序序列建成一个堆?
- 如何在输出堆顶元素后,调整剩余元素为一个新的堆?
堆的调整——小根堆:
- 输出堆顶元素后,以堆中
最后一个元素替代之;- 然后将根节点值与左、右子树的根节点值进行比较,并与其中
小者进行交换;- 重复上述操作,直至叶子节点,将得到新的堆,称这个从堆顶至叶子的调整过程为
“筛选”。
堆的建立:
- 单节点的二叉树是堆;
- 在完全二叉树中所有以叶子节点(序号i⩾n/2i \geqslant n/2i⩾n/2)为根的子树是堆;
- 这样,只需依次将以序号为 n/2,n/2−1,...,1n/2, n/2-1, ..., 1n/2,n/2−1,...,1 的节点为根的子树均调整为堆即可,即:对应由 nnn 个元素组成的无序序列,“筛选”只需从第 n/2n/2n/2 个元素开始。
性能分析:
- 初始堆化所需时间不超过O(n)O(n)O(n);
- 排序阶段(不含初始堆化)
一次重新堆化所需时间不超过O(logn)O(logn)O(logn);
n−1n-1n−1 次循环所需时间不超过O(nlogn)O(nlogn)O(nlogn);
Tw(n)=O(n)+O(nlogn)=O(nlogn)Tw(n) = O(n) + O(nlogn) = O(nlogn)Tw(n)=O(n)+O(nlogn)=O(nlogn)稳定性:
不稳定。
#include <iostream>
#include <vector>
using namespace std;/*
* @brief: 将v[start~end]的记录调整为一个大顶堆
* 已知v[start~end]中的记录除v[start]外均满足堆的定义
* @param v: 待调整序列引用
*/
void heapAdjust(vector<int>& v, int start, int end)
{int temp = v[start];for (size_t j = 2 * start; j <= end; j *= 2) // 沿关键字较大的孩子节点向下筛选{if (j < end && v[j] < v[j + 1]) // j:左孩子 j+1:右孩子{++j; // 右孩子较大,将j增1}if (temp >= v[j]){break; // temp的值比左右孩子值都大,不需要调整}v[start] = v[j]; // 将较大的孩子节点上调至父节点start = j;// j *= 2:继续对较大孩子节点进行调整}v[start] = temp;
}/*
* @brief: 堆排序
* @param v: 待排序序列引用
*/
void heapSort(vector<int>& v)
{int length = v.size() - 1; // 完全二叉树、堆顶元素从1开始编号,所以我们对v// 这里减1是为了不考虑v[0],只对v[1~length]排序// 初始堆化for (size_t i = length / 2; i > 0; i--){heapAdjust(v, i, length);}for (size_t i = length; i > 1; i--){// 将堆顶元素与最后一个元素交换int temp = v[1];v[1] = v[i];v[i] = temp;// 将v[1~i-1]再调整称大顶堆heapAdjust(v, 1, i - 1);}
}/*
* @brief: 打印元素
* @param v: 待排序序列引用
*/
void printVec(vector<int>& v)
{for (size_t i = 1; i < v.size(); i++){cout << v[i] << "\t";}cout << endl;
}int main(int argc, char* argv[])
{vector<int> v = { 0,81,94,11,96,12,35,17,95,28,58,41,75,15 };cout << "排序前:" << endl;printVec(v);// 排序heapSort(v);cout << "排序后:" << endl;printVec(v);
}

四、归并排序
基本思想:
将两个或两个以上的有序子序列“归并”为一个有序序列。在内部排序中,通常采用的是2-路归并排序,即:将两个位置相邻的有序子序列R[l...m]R[l...m]R[l...m]和R[m+1...n]R[m+1...n]R[m+1...n]归并为一个有序序列R[l...m]R[l...m]R[l...m]。
性能分析:
- 时间效率:O(nlogn)O(nlogn)O(nlogn);
- 空间效率:O(n)O(n)O(n);
稳定性:
稳定。
#include <iostream>
#include <vector>
using namespace std;/**
* @brief: 将有序序列vSrc[s...m]和vSrc[m+1...t]合并到vDst[s...t]
* @param vSrc: 源数组引用
* @param vDst: 目标数组引用
* @param s: start index
* @param m: 'middle' index, s < m < t
* @param t: end index
*/
void merge(vector<int>& vSrc, vector<int>& vDst, int s, int m, int t)
{int i = s, j = m + 1;int k = s;while (i <= m && j <= t){if (vSrc[i] < vSrc[j]){vDst[k++] = vSrc[i++];}else{vDst[k++] = vSrc[j++];}}while (i <= m){vDst[k++] = vSrc[i++];}while (j <= t){vDst[k++] = vSrc[j++];}
}/*
* @brief: 归并排序,将vSrc[s...t]归并排序为vDst[s...t]
* @param vSrc: 待排序序列引用
* @param vDst: 排序结果序列引用
* @param s: start index
* @param t: end index
*/
void mergeSort(vector<int>& vSrc, vector<int>& vDst, int s, int t)
{if (s == t){vDst[s] = vSrc[s];return;}else{int m = (s + t) / 2;vector<int> vTemp(vSrc.size());mergeSort(vSrc, vTemp, s, m);mergeSort(vSrc, vTemp, m + 1, t);merge(vTemp, vDst, s, m, t);}
}/*
* @brief: 打印元素
* @param v: 待排序序列引用
*/
void printVec(vector<int>& v)
{for (size_t i = 0; i < v.size(); i++){cout << v[i] << "\t";}cout << endl;
}int main(int argc, char* argv[])
{vector<int> v = { 81,94,11,96,12,35,17,95,28,58,41,75,15 };cout << "排序前:" << endl;printVec(v);// 排序int length = v.size();vector<int> vRes(length);cout << "aa" << endl;mergeSort(v, vRes, 0, length - 1);cout << "排序后:" << endl;printVec(vRes);
}

五、各种排序方法比较
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 直接插入排序 | O(n2)O(n^2)O(n2) | O(n)O(n)O(n) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 稳定 |
| 希尔排序 | O(nlogn)O(nlogn)O(nlogn)~O(n2)O(n^2)O(n2) | O(n1.3)O(n^{1.3})O(n1.3) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 不稳定 |
| 冒泡排序 | O(n2)O(n^2)O(n2) | O(n)O(n)O(n) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 稳定 |
| 快速排序 | O(nlogn)O(nlogn)O(nlogn) | O(nlogn)O(nlogn)O(nlogn) | O(n2)O(n^2)O(n2) | O(logn)O(logn)O(logn)~O(n)O(n)O(n) | 不稳定 |
| 简单选择排序 | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 稳定 |
| 堆排序 | O(nlogn)O(nlogn)O(nlogn) | O(nlogn)O(nlogn)O(nlogn) | O(nlogn)O(nlogn)O(nlogn) | O(1)O(1)O(1) | 不稳定 |
| 归并排序 | O(nlogn)O(nlogn)O(nlogn) | O(nlogn)O(nlogn)O(nlogn) | O(nlogn)O(nlogn)O(nlogn) | O(n)O(n)O(n) | 稳定 |
参考链接
青岛大学数据结构-王卓
相关文章:

四类(七种)排序算法总结
一、插入排序 基本思想: 每次将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。即边插入边排序,保证子序列中随时都是排好序的。 基本操作——有序插入ÿ…...

[oeasy]python0083_十进制数如何存入计算机_八卦纪事_BCD编码_Binary_Coded_Decimal
编码进化 回忆上次内容 上次 研究了 视频终端的 演化 从VT05 到 VT100从 黑底绿字 到 RGB 24位真彩色形成了 VT100选项 从而 将颜色 数字化 了 生活中我们更常用 10个数字 但是 计算机中 用二进制 日常计数的十进制数 是如何存储进计算机的呢?🤔 从10进制到2进…...

理解框架的编译时与运行时
首先我们需要先理解一下什么事编译时和运行时 在语言层面,先来聊一下前端开发者最常遇见的两种语言JavaScript和Java Java的代码就是被编译为.class 文件才能运行,这个编译过程就是编译时,运行 .class 文件就是运行时我们在浏览器直接输入一…...
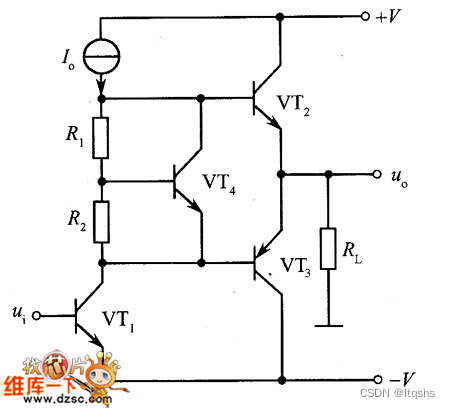
推挽电路---采用二极管消除交越失真----克服交越失真的互补推挽输出电路图
交越失真产生的原因及消除方法 由于晶体管的门限电压不为零,比如一般的硅三极管,NPN型在0.7V以上才导通,这样在00.7就存在死区,不能完全模拟出输入信号波形,PNP型小于-0.7V才导通,比如当输入的交流的正弦波…...

day11_面向对象
今日内容 零、 复习昨日 一、一日一题(数组,OOP) 二、面向对象练习(方法参数返回值) 三、局部变量&成员变量 四、this关键字 五、构造方法 六、重载 七、封装 小破站同步上课视频: https://space.bilibili.com/402601570/channel/collectiondetail?…...
大数据处理学习笔记1.1 搭建Scala开发环境
文章目录零、本讲学习目标一、Scala简介(一)Scala概述(二)函数式编程(三)Scala特性1、一切都是对象2、一切都是函数3、一切都是表达式(四)在线运行Scala二、选择Scala版本三、Window…...

VSCODE C++ 调用matplotlibcpp画图
使用VSCODE编写C程序,想在调试过程中看中间数据的波形,于是找到了python的matplotlibcpp库,参考文章链接是:https://blog.csdn.net/weixin_43769166/article/details/118365416;按照他的步骤配置好之后,跳出…...
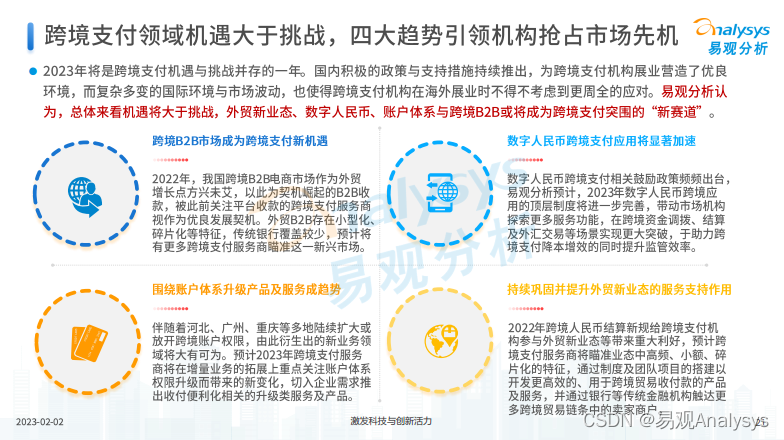
面对“开门红”,跨境支付如何寻求新增长曲线?
易观:2022年是第三方支付行业洗牌加剧的一年,在部分机构选择退出的过程中,也有机构开始瞄准跨境业务,成为了支付机构转型的重要方向之一。跨境支付是指两个或及其以上的国家或地区进行国际贸易、国际投资或其他经济活动࿰…...
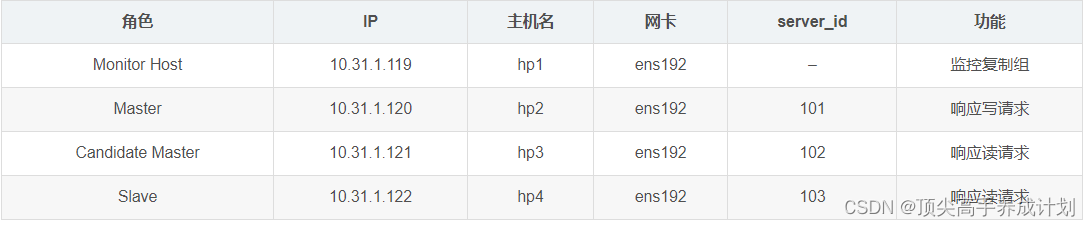
MySQL入门篇-MySQL MHA高可用实战
MHA简介 MHA(Master High Availability)目前在MySQL高可用方面是一个相对成熟的解决方案,它由日本DeNA公司的youshimaton(现就职于Facebook公司)开发,是一套优秀的作为MySQL高可用性环境下故障切换和主从提…...
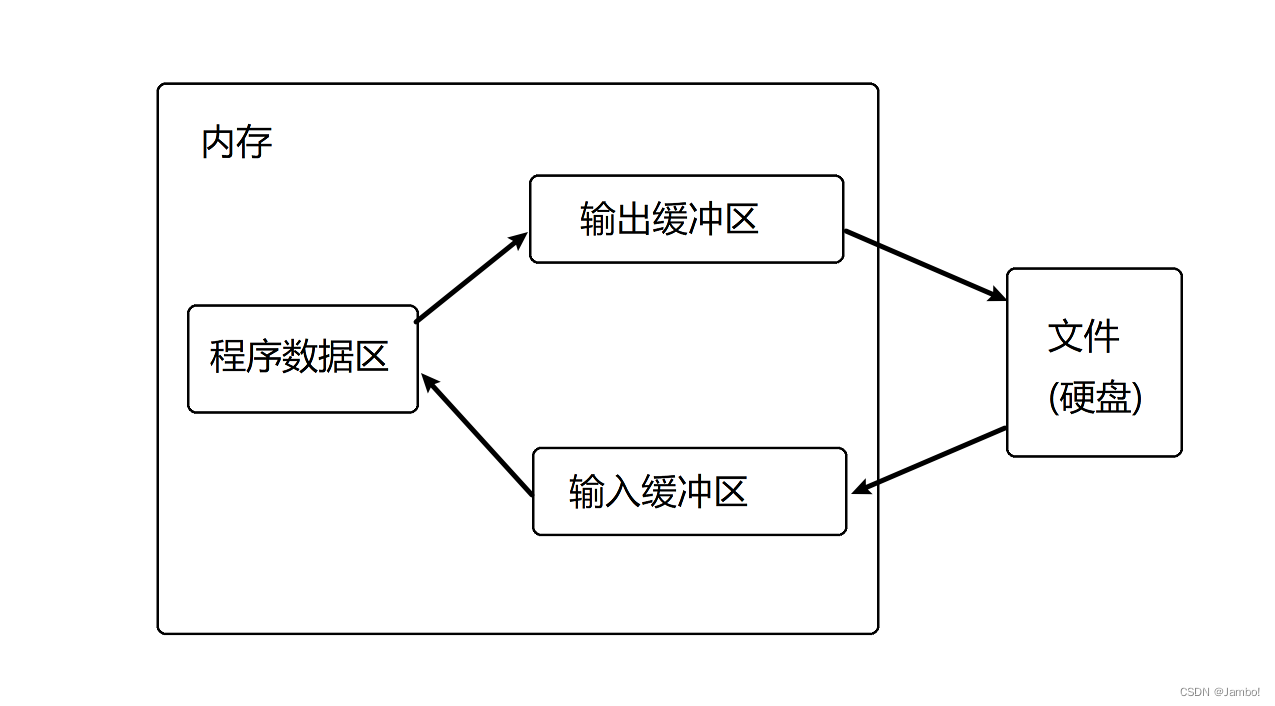
C语言文件操作
目录1.文件指针2.文件的打开和关闭3.文件的读写3.1文件的顺序读写fgetc和fputcfgets和fputsfscanf和fprintffread和fwrite3.2文件的随机读写fseekftellrewind4.文本文件和二进制文件5.文件读取结束的判定6.文件缓冲区1.文件指针 在文件操作中,一个关键的概念是文件…...
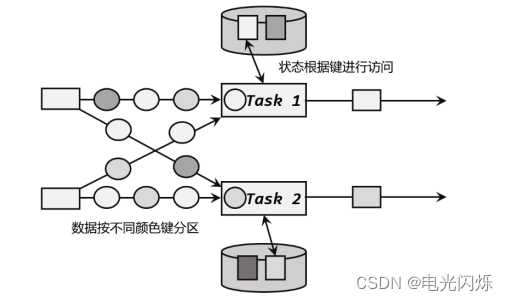
Flink中核心重点总结
目录 1. 算子链 1.1. 一对一(One-to-one, forwarding) 1.2. 重分区(Redistributing) 1.3. 为什么有算子链 2. 物理分区(Physical Partitioning) 2.1. 什么是分区 2.2. 随机分区ÿ…...

gismo中NURBS的相关函数的使用---待完善
文章目录 前言一、B样条的求值1.1 节点向量的生成1.2 基函数的调用1.3 函数里面的T指的是系数类型二、以等几何两个单元12个控制点为例输出的控制点坐标有误1.4二、#pic_center <table><tr><td bgcolor=PowderBlue>二维数2.12.22.32.4三、3.13.23.33.4四、4.…...

5.数据共享与持久化
数据共享与持久化 在容器中管理数据主要有两种方式: 数据卷(Data Volumes)挂载主机目录 (Bind mounts) 数据卷 数据卷是一个可供一个或多个容器使用的特殊目录,它绕过UFS,可以提供很多有用的特性: 数据…...

RabbitMQ-客户端源码之AMQCommand
AMQCommand不是直接包含Method等成员变量的,而是通过CommandAssembler又做了一次封装。 接下来先看下CommandAssembler类。此类中有这些成员变量: /** Current state, used to decide how to handle each incoming frame. */ private enum CAState {EXP…...

linux设置登录失败处理功能(密码错误次数限制、pam_tally2.so模块)和操作超时退出功能(/etc/profile)
一、登录失败处理功能策略 1、登录失败处理功能策略(服务器终端) (1)编辑系统/etc/pam.d/system-auth 文件,在 auth 字段所在的那一部分添加如下pam_tally2.so模块的策略参数: auth required pam_tally2…...

Centos7上Docker安装
文章目录1.Docker常识2.安装Docker1.卸载旧版本Docker2.安装Docker3.启动Docker4.配置镜像加速前天开学啦~所以可以回来继续卷了哈哈哈,放假在家效率不高,在学校事情也少点(^_−)☆昨天和今天学了学Docker相关的知识,也算是简单了解了下&…...

新瑞鹏“狂飙”,宠物医疗是门好生意吗?
宠物看病比人还贵,正在让不少年轻一族陷入尴尬境地。在知乎上,有个高赞提问叫“你愿意花光积蓄,给宠物治病吗”,这个在老一辈人看来不可思议的魔幻选择,真实地发生在当下的年轻人身上。提问底下,有人表示自…...
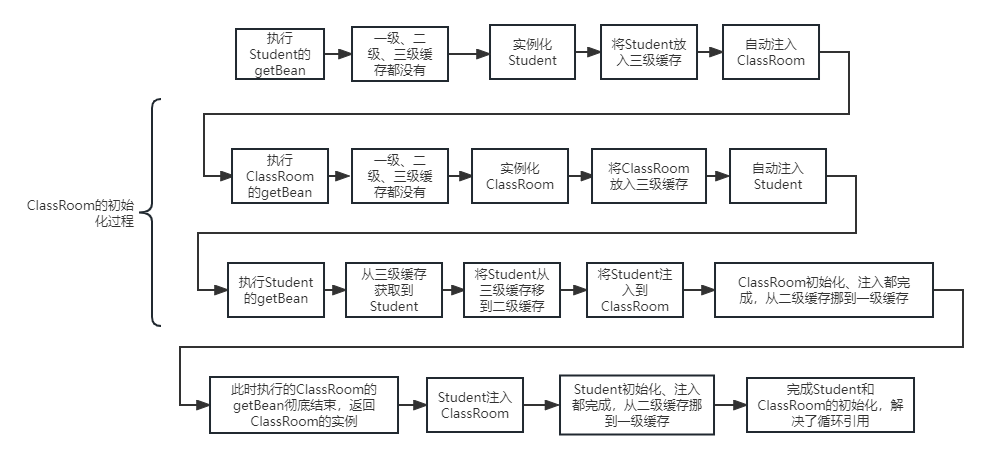
Spring循环依赖问题,Spring是如何解决循环依赖的?
文章目录一、什么是循环依赖1、代码实例2、重要信息二、源码分析1、初始化Student对Student中的ClassRoom进行Autowire操作2、Student的自动注入ClassRoom时,又对ClassRoom的初始化3、ClassRoom的初始化,又执行自动注入Student的逻辑4、Student注入Class…...
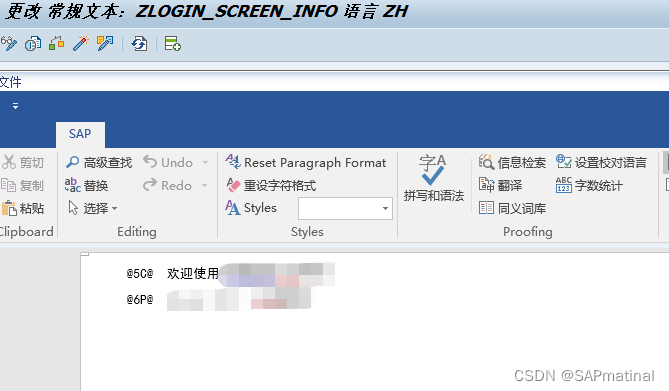
更改SAP GUI登录界面信息
在SAP GUI的登录界面,左部输入登录信息如客户端、用户名、密码等,右部空余部分可维护一些登录信息文本,如登录的产品、客户端说明及注意事项等,此项操作详见SAP Notes 205487 – Own text on SAPGui logon screen 维护文档使用的…...
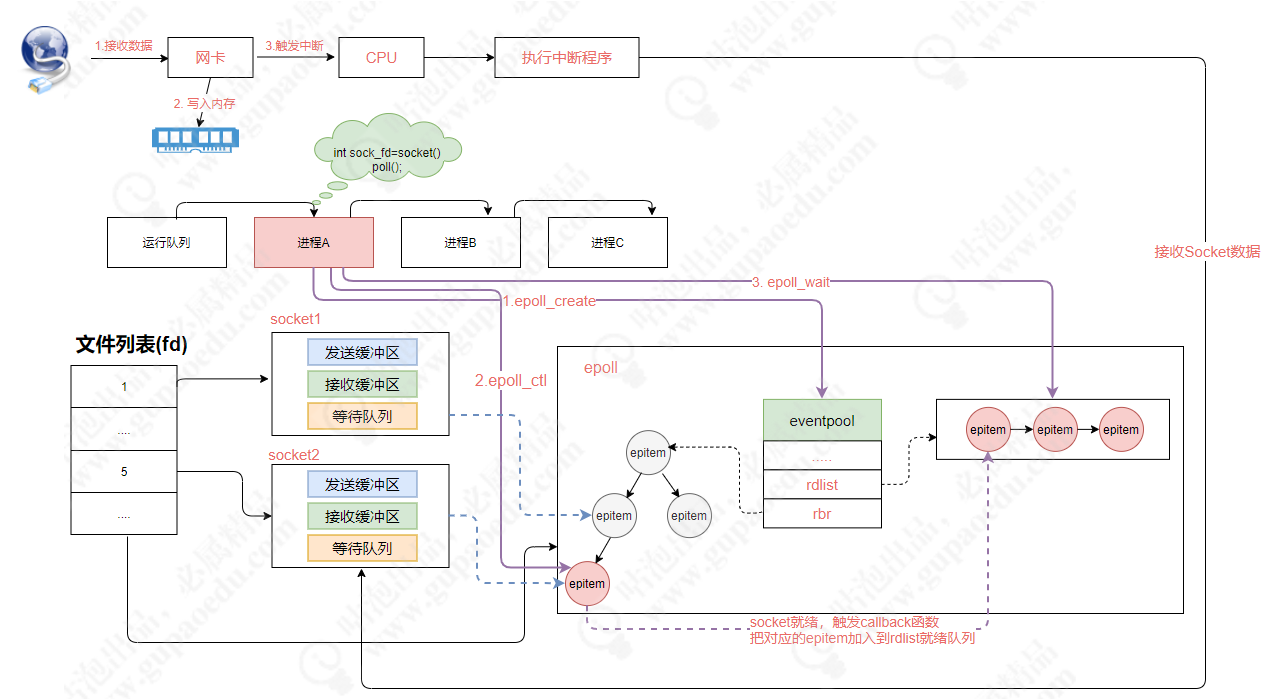
分布式微服务架构下网络通信的底层实现原理
在分布式架构中,网络通信是底层基础,没有网络,也就没有所谓的分布式架构。只有通过网络才能使得一大片机器互相协作,共同完成一件事情。 同样,在大规模的系统架构中,应用吞吐量上不去、网络存在通信延迟、我…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
