剑指 Offer 51. 数组中的逆序对
剑指 Offer 51. 数组中的逆序对
难度:hard\color{red}{hard}hard
题目描述
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 1:
输入: [7,5,6,4]
输出: 5
限制:
0<=数组长度<=500000 <= 数组长度 <= 500000<=数组长度<=50000
算法
(归并排序)
首先先看一张图:
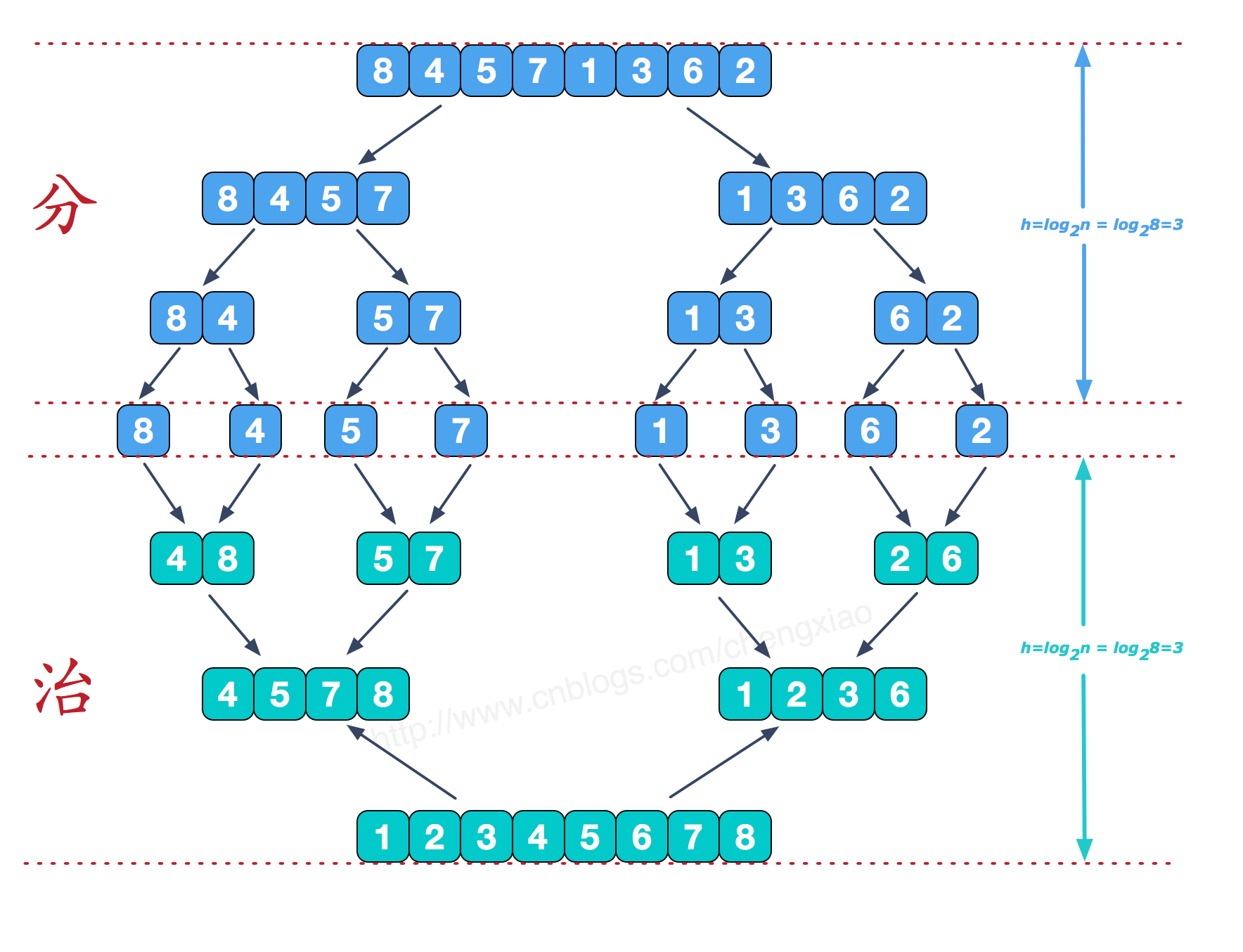
1. 逆序对的定义:
对于数列的第 i 个和第 j 个元素,如果满足 i < j 且 a[i] > a[j],则其为一个逆序对。
重要的地方在于,一个元素可以不只是在一个逆序对中存在。如果 k > j > i 且 a[i] > a[j] > a[k],那么这里
有两个含 a[i] 的逆序对,分别是 (a[i], a[j]) 和 (a[i], a[k]), a[i]是可以使用多次的。
(太长不看)
举个栗子:
num: 2 3 4 5 6 1
id : 0 1 2 3 4 5
一句话概括就是求当前数组中存在几个比当前位置大的,(或者后面有几个数字比他小的) 加上2在第一个位置,后面比它小的数字是1,所以2的逆序对是(2, 1), 同理(3, 1) (4, 1) (5, 1) (6, 1)
答案是5。
2. 分析问题:
采用分治法来求解问题,为什么不是树状数组呢~~(buhui)~~,因为分治法求解此题比较简单。
按照y总的说法:我们将序列从中间分开,将逆序对分成三类:
- 两个元素都在左边;
- 两个元素都在右边;
- 两个元素一个在左一个在右;
算法的大致框架为:
- 递归算左边\color{red}{左边}左边的;
- 递归算右边\color{red}{右边}右边的;
- 算一个左一个右\color{red}{一个左一个右}一个左一个右的;
- 把三个结果加在一起
3. 问题详解:
- 在一些题解中说到可以不用计算前两种情况,只需要看第三种情况,我的理解是:需要真正知道归并排序在做什么。这就是我们上面的那张图,归并排序分为两个大步骤;分\color{red}{分}分和治\color{red}{治}治,从上面的栗子中我们看出,分的步骤会把所有的数组分为一个单独的数字,所以也就解释了为什么不需要考虑前两种情况,最种都会到第三中情况上,因为只有每组只有一个数字,它没有人同组,1就是1,怎么变成2,
我就吃了一碗粉,为什么付两碗的钱。所以最终都是会变成第三种情况。 - 下面解释治.
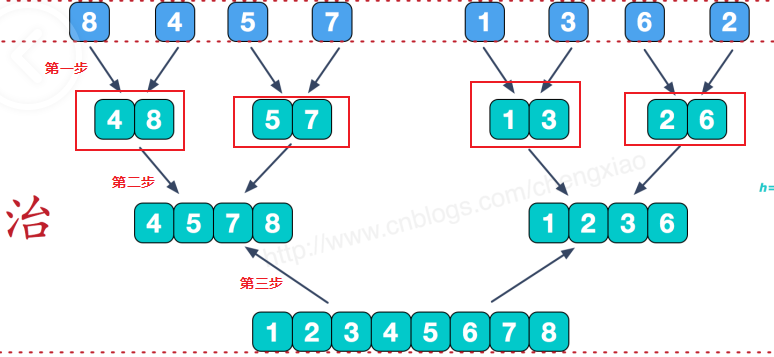
- 第一步对元素进行排序,可以看到直接是求两个单独元素的逆序对,如果是逆序对,答案ans++,然后合并两个数字变成一个有序的数组,
- 第二步,在对两个分组的数字进行求逆序对,此时没有到只剩下两个分组的情况,可以把这些步骤看作是内部之间求逆序对。
- 第三步就是两个分组求逆序对。可以看到此时前后两个分组都是有序的,前面的数组的下边为
l..mid,后面的下标为mid + 1...r,我们可以在归并的时候是需要把两个数组的值重新赋值到原数组中的,所以就可以比较两个数组的值,也就是可以求逆序对。如果A数组的值q[i]大于B数组的值q[j],代表在A数组中i~mid都是大于q[j]的,所以对于q[j]来说他的逆序对数量为mid - i + 1,同理,其他的逆序对也可以这么求。
复杂度分析
-
时间复杂度:O(nlogn)O(n logn)O(nlogn),其中 nnn 是链表的长度。需要遍历链表一次
-
空间复杂度 : O(n)O(n)O(n),因为归并排序需要用到一个临时数组。
C++ 代码
class Solution {
public:int reversePairs(vector<int>& nums) {return merge_sort(nums, 0, nums.size() - 1);}int merge_sort(vector<int>& nums, int l, int r){if (l >= r) return 0;int mid = (l + r) / 2;// 分int res = merge_sort(nums, l, mid) + merge_sort(nums, mid + 1, r);// 并int i = l, j = mid + 1, k = 0;vector<int> temp;while (i <= mid && j <= r){if (nums[i] <= nums[j]) temp.push_back(nums[i ++]);else{res += mid - i + 1;temp.push_back(nums[j ++]);}}while (i <= mid) temp.push_back(nums[i ++]);while (j <= r) temp.push_back(nums[j ++]);i = l;for (auto x : temp) nums[i ++] = x;return res;}
};
相关文章:

剑指 Offer 51. 数组中的逆序对
剑指 Offer 51. 数组中的逆序对 难度:hard\color{red}{hard}hard 题目描述 在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。 示例 1: 输入: [7…...
数字化转型迫在眉睫!药企如何应用AI技术加速创新?
导语 | 近年来,随着 AI 等技术的发展应用,数字化、智能化日渐成为各行各业转型升级的新兴力量,其与医药产业的融合创新也逐渐成为当前的新趋势,众多医药制造企业蓄势待发,搭乘数字化的快车,驶入高速发展的快…...

电脑显示屏是怎么显示出图像的?CPU与GPU又是什么关系?
文章目录电脑显示屏是怎么显示出图像的?CPU与GPU又是什么关系?显卡作用明明有了CPU为什么还要GPU?电脑显示屏是怎么显示出图像的?内存与显存所有运算都交给GPU处理可以吗?参考:电脑显示屏是怎么显示出图像的ÿ…...

报名截至在即 | “泰迪杯”挑战赛最后一场赛前指导直播!
为推广我国高校数据挖掘实践教学,培养学生数据挖掘的应用和创新能力,增加校企交流合作和信息共享,提升我国高校的教学质量和企业的竞争能力,第十一届“泰迪杯”数据挖掘挑战赛(以下简称挑战赛)已于2023年3月…...

经验分享:如何有效应对Facebook广告数据波动问题?
Facebook广告作为一种重要的数字营销工具,可以帮助企业和品牌快速获得目标受众的关注和转化。然而,由于广告投放过程的不稳定性,Facebook广告数据波动问题也经常出现。 对于广告主而言,如何应对Facebook广告数据波动问题…...
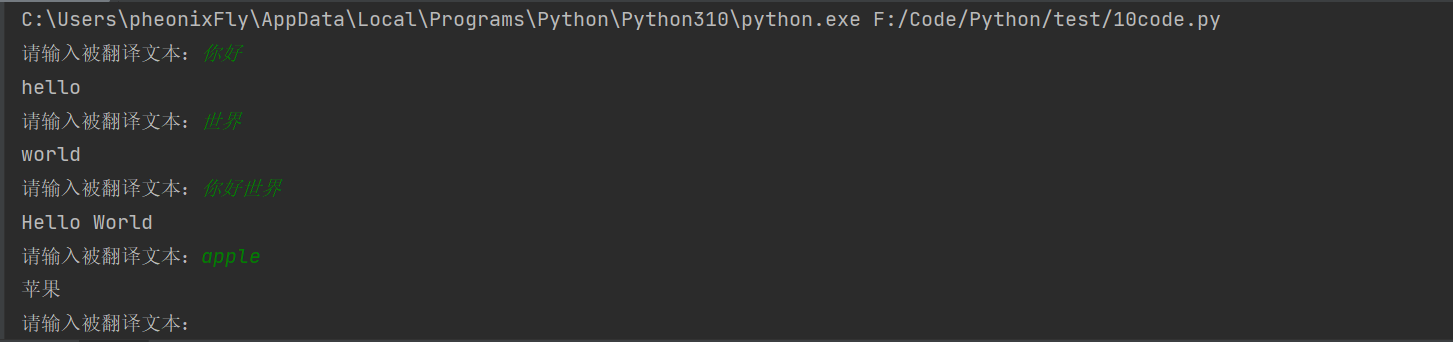
【Python】逆向解析js代码
目录 1. 打开百度翻译网页,查找翻译结果的网络资源包 2. 获取翻译结果网络资源包的url、请求头、请求体,解析json文件数据 3. 观察请求体字段,发现 query 字段便是我们输入的需要翻译的值 4. ctrl F 快捷键搜索sign值的网络资源包&#x…...
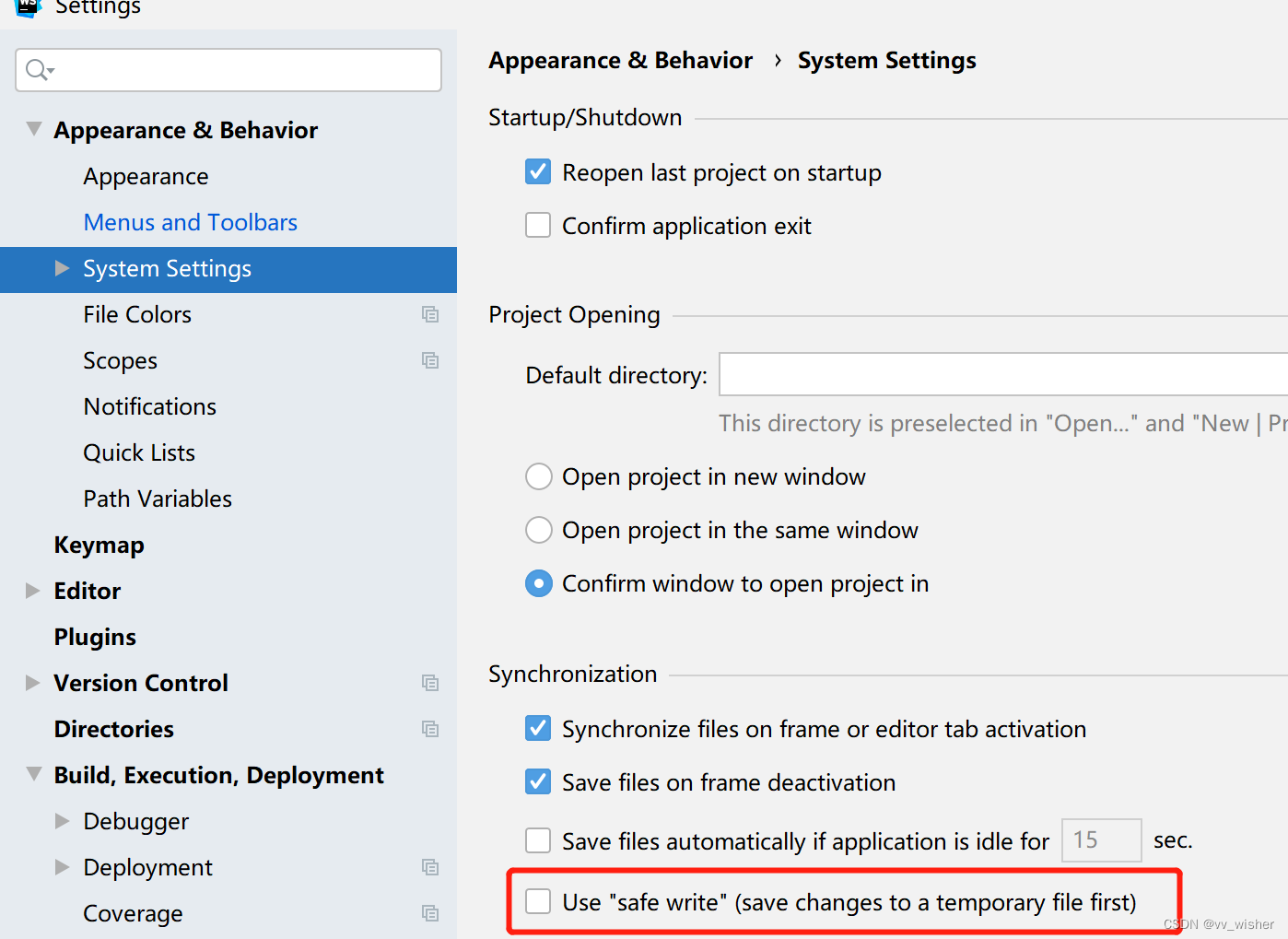
websorm启动vue项目修改内容后自动运行内存溢出
手动启动vue项目正常运行,修改部分内容保存后会自动重新run一下, 这个时候就报错内存溢出,然后很悲伤的需要再手动重启一下。 (在网上查了好多方法就不单独加链接了) 前3个方法都试过对于我的项目无效,第4…...
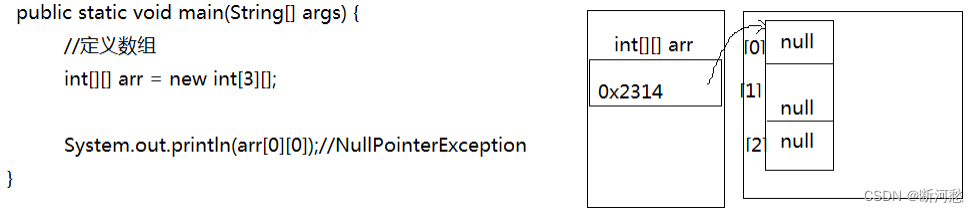
第05章_数组
第05章_数组 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 本章专题与脉络 1. 数组的概述 1.1 为什么需要数组 需求分析1: 需要统计某公司50个员工的工资情况,例如计…...
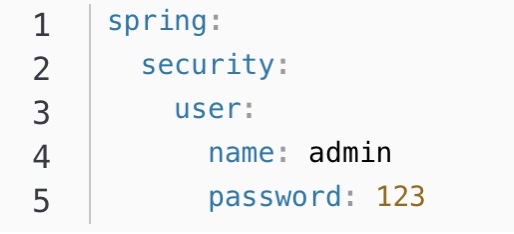
Spring Security --- 快速入门
概念 Spring Security是一个功能强大且高度可定制的,主要负责为Java程序提供声明式的 身份验证和访问控制 的安全框架Spring Security的底层主要是 基于 Spring AOP 和 Servlet 过滤器 来实现安全控制它提供了全面的安全解决方案同时授权粒度可以在 Web请求级和方法…...
程序员挣够了钱,到中年失业真的很可怕吗?
借用最近很火的一张图,看看没有工作,你手里的存款够用几年(按每年年化3.5%,利息继续放入理财计算): 如果每年花销在10万左右(折合每个月8333元,应该是比较富足的)&#x…...

【Log and Dump Summary】
开各模块log前,建议先关闭selinux权限,并确定camera logD是已经有打印的,如果没有打印可以用如下命令开启: adb shell setenforce 0adb shell setprop persist.vendor.mtk.camera.log_level 3 adb shell pkill camera*再按以下方法开对应模块的 log: 1. 开MTK Camera2 …...

软考证书找工作有用吗?软考找工作用处大吗
软考证书是衡量IT技术人才能力的一种重要评价标准。 一、软考高级证书对找工作的帮助 1. 竞争力增强 软考高级证书具有一定难度和较高的专业技能要求,拥有该证书的人的技术水平和专业能力会得到认可和尊重,从而增强求职者的竞争力。 2. 拓宽职业发展…...

JavaWeb之谈论项目编码规范_Java版
1. 关于DDD项目结构约定 1.1 项目结构使用DDD整洁架构进行分包 maven项目结构遵从DDD整洁架构分为如下四个顶级包: application - 应用层代码,一般为接口层定义API的实现类和一些结构转化,application不应该承载业务逻辑 domain - 领域层&a…...

Map排序
(一)treeHap 特点:treeMap中的元素根据键的大小自然排序(默认是升序) 1、treeHap遍历测试 import java.io.IOException; import java.util.*; public class Main {public static void main(String[] args)throws IOException {…...

mycat读写分离
1.准备工作 tar包 http://dl.mycat.org.cn/2.0/install-template/mycat2-install-template-1.20.zip jar包 http://dl.mycat.org.cn/2.0/1.21-release/ (下载最新的jar包) 将下载好的jar放到tar中的lib目录下并放入linux系统中 2.创建逻辑库 连接mycat端口8066 账号root 密码12…...

[Linux]环境变量
目录 基本概念 常见的环境变量 PATH测试 HOME测试 SHELL测试 和环境变量相关的命令 main函数的三个参数 环境变量的组织方式 通过代码如何获取环境变量 通过系统调用获取或设置环境变量 基本概念 环境变量(environment variables)一般是指在操作系统中用来指定操作系…...

次优二叉查找树(次优查找树)_递归和非递归实现_20230414
次优二叉查找树(次优查找树)-递归和非递归实现 前言 当有序表中的各记录的查找概率相等的时候,采用折半查找效率可以提升查找性能;如果有序表中的各记录的查找概率不相等,那么折半查找就不再适用。 如果只考虑查找成功的情况&a…...

贯穿设计模式第八话--设计原则总结篇
🥳🥳🥳 茫茫人海千千万万,感谢这一刻你看到了我的文章,感谢观赏,大家好呀,我是最爱吃鱼罐头,大家可以叫鱼罐头呦~🥳🥳🥳 从今天开始,将…...
在水文水资源、水环境中的实践技术应用及案例分析)
地理信息系统(ArcGIS)在水文水资源、水环境中的实践技术应用及案例分析
目录 专题一 ArcGIS:数据管理 专题二 ArcGIS:数据转换 专题三 ArcGIS:地图制作 专题四 水文水环境数据编辑与管理 专题五 水文水环境数据处理与分析 专题六 ArcGIS水文分析及流域特征提取 专题七 湖泊水库水环境监测及评价 专题八 河…...
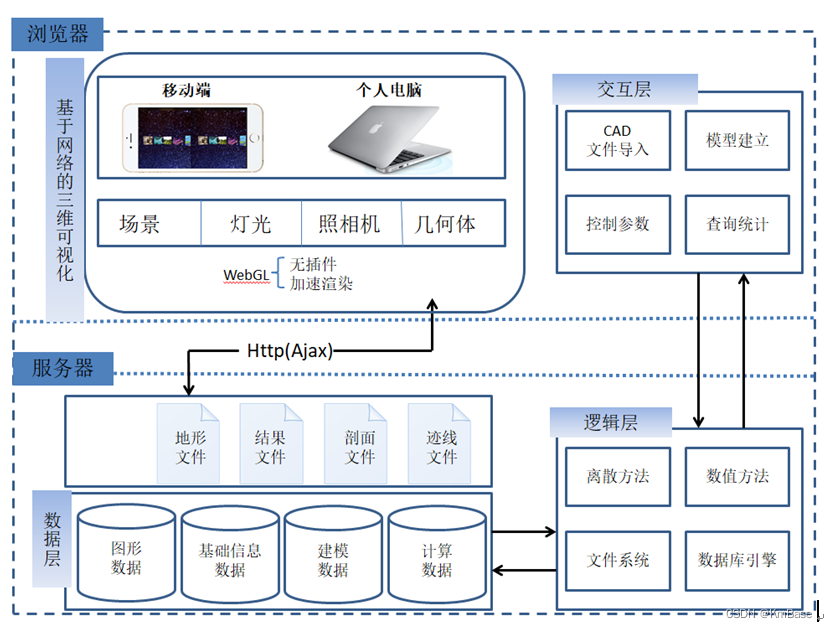
部分国产水文水动力模型介绍
一、HydroMPM模型 1、模型介绍 2016年度自立项目HydroMPM系统开发与集成完成的洪水分析模拟软件等成果经权威专家鉴定整体达到国际领先水平,HydroMPM_FloodRisk入选国家防总《全国重点地区洪水风险图编制项目可选软件名录》。成果应用项目100余项,累计…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
