期权价格上下限与期权平价关系
目录
1. 期权的基本概念
2. 期权的上下限
3. 期权的平价关系
1. 期权的基本概念
期权:是一种选择权,期权买方向卖方支付一定数额的 期权费 后,可获得在 一定时间(到期日)内以 一定价格(执行价格)买入或者卖出 一定数量标的物 的 权利。
1. 到期日 Expire:期权合约预先指定的将来履行合约的具体时间,又称偿还日。
2. 执行价 Strike:期权合约确定的标的资产的交割价格,又称履约价格。
3. 期权费:期权是花钱买/卖未来买/卖标的物的权利,期权合约代表着一种主动权。所以期权本身是有其价值的,这个价值就是期权费,即这个权利值多少钱。
4. 期权买方 Long:买入期权的一方,期权多头。
5. 期权卖方 Short:卖出期权的一方,期权空头。
6. 买权 Call option:持有者拥有未来按执行价买入标的物的权利,也叫看涨期权。
7. 卖权 Put option:持有者拥有未来按执行价卖出标的物的权利,也叫看跌期权。
8. 欧式期权:持有者只能在到期日才能履行合约。
9. 美式期权:持有者在到期日之前的任何时间(包括到期日)都可以履行合约。
10. 实值期权:持有者通过执行期权会产生正现金流的期权,价内期权。
11. 平值期权:现金流接近于零的期权为平值期权,平价期权。
12. 虚值期权:现金流为负的期权,价外期权。
是实值还是虚值仅取决于执行期权权利的现金流收入为正还是为负,与总收益为正还是为负无关,即不考虑期权费。
13. 内在价值:期权如果现在就执行(假如可以的话),执行期权给持有人带来的损益与 0 比较,更大的那个。
- 买权的内在价值:max(S - X, 0)
- 卖权的内在价值:max(X - S, 0)
14. 时间价值:期权费减去内在价值的部分。
期权的价值来自于不确定性,距离到期时间越长不确定性越大。这部分不确定性的价值体现在对期权卖方承担无限风险的补偿,或者表现为期权持有者获得收益的可能性,这就是期权费减去期权内在价值的部分。
2. 期权的上下限
(上限)
欧式或美式看涨期权 的持有者有权以某一价格买入某标的物,看涨期权价格的 C 不会超过标的物价格 S:C ≤ S
C 是买东西的一项权利,如果这个权利的价格比标的物还贵,那么直接去市场买标的物就完事儿了。比如,买入价值为 S 的标的物,再卖出价值为 C 的权利,则目前的收益是 C - S 。如果到时候标的物跌了,那么对方不履约,我可以啥都不用做,最终收益也为 C - S;如果到时候标的物涨了,对方履约以 X 价买我的标的物,我直接把手里的标的物给 TA,还能得到 X,最终收益为 C - S + X 。
欧式或美式看跌期权 的持有者有权以 X 的价格卖出某标的物,不论标的物的市场价降为多少,看跌期权的价格 P 不会超过执行价格 X:P ≤ X
P 是卖东西的一项权利,如果这个权利的价格比执行价格还高,那么直接卖掉这个权利就完事儿了,我还能留着我的标的物。
对于欧式期权,现在期权的价格 p:
因为欧式期权不能提前执行,所以需要把执行价格 X 按连续复利方式进行折现。
(下限)
在不支付红利的情况下,欧式看涨期权 的下限为:
假设现在借入一份股票并卖出得到
,再花费
买入一份看涨期权,剩余
,将这笔钱进行无风险投资。在 T 时刻,这笔钱变为 X,恰好能够以 X 买入一份股票进行平仓。如果 c 小于
,则在 T 时刻,这笔钱将会大于 X,平仓后还有剩余的钱。
在支付红利的情况下,欧式看涨期权 的下限为:
其中 是标的资产在 t 时刻的价格,D 是期权有效期内标的资产收益的折现。
至于为什么是 - D,这个在远期合约定价里面讲过。
在不支付红利的情况下,欧式看跌期权 的下限为:
在支付红利的情况下,欧式看跌期权 的下限为:
其中 是标的资产在 t 时刻的价格,D 是期权有效期内标的资产收益的折现。
3. 期权的平价关系
假设持有执行价格为 X 的,一份欧式 看跌期权多头 P,一份欧式 看涨期权空头 C,加一单位现价为 S 的 股票多头,即总价值是 S+P-C 的投资组合。
为什么做空头就是减号?因为 C 对应的是看涨期权的价值,如果到期日股价高于执行价格,那么期权持有者将会执行期权,TA 倒是获得了价值为 C 的收益,但你这个空头就要损失 C,因此这里使用的减号。

整理可得:
或者:
这就是 期权的平价关系,也就是看涨期权和看跌期权价格会保持在一个均衡水平。(如果知道一种期权价格,可以用平价关系求另一种期权价格)
但在实际中,考虑到交易成本等因素,期权平价关系左右两边并不相等,而是有一定误差。只要误差在可接受范围内都算期权平价关系成立。
相关文章:
期权价格上下限与期权平价关系
目录 1. 期权的基本概念 2. 期权的上下限 3. 期权的平价关系 1. 期权的基本概念 期权:是一种选择权,期权买方向卖方支付一定数额的 期权费 后,可获得在 一定时间(到期日)内以 一定价格(执行价格&#x…...
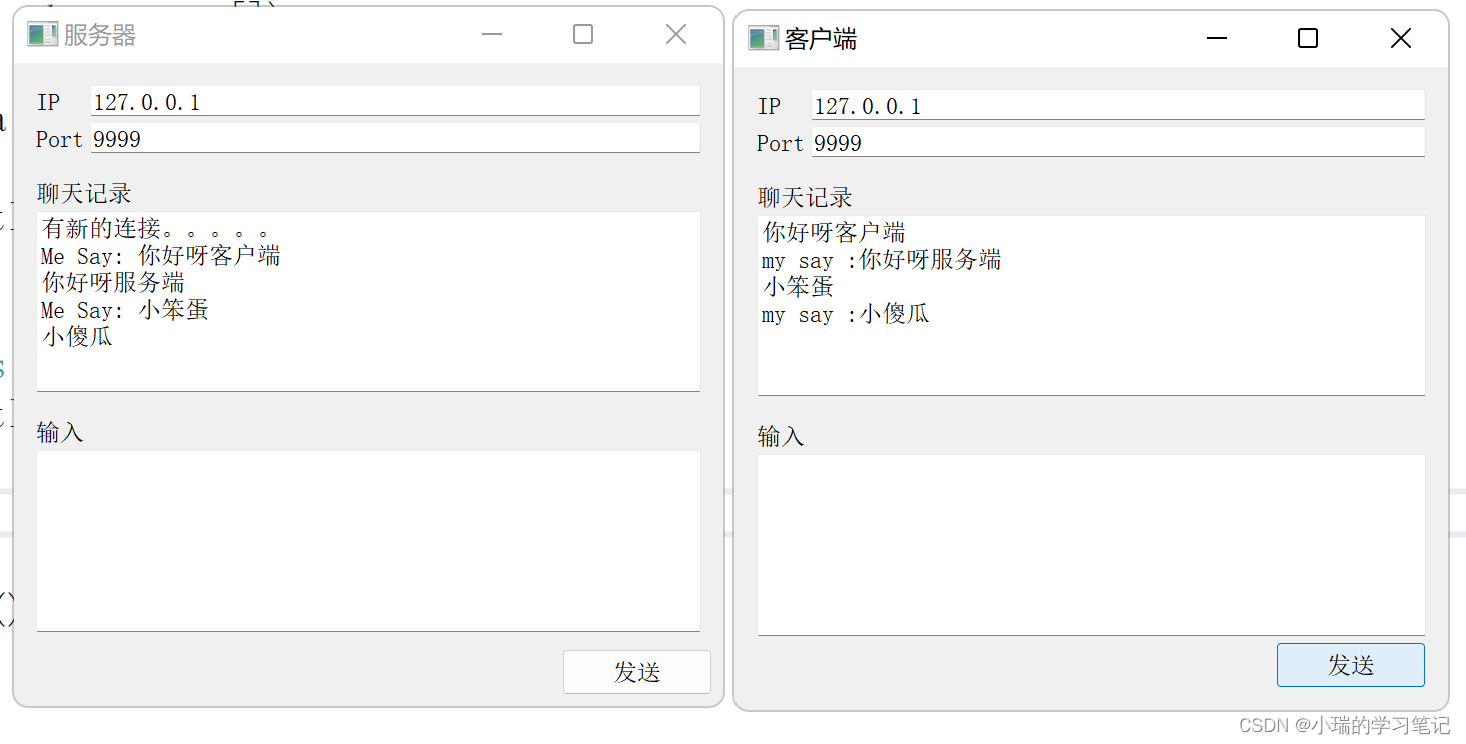
QT中TCP的学习
文章目录 qt中TCP的实现 qt中TCP的实现 学习视频 QT中可以通过TCP协议让服务器和客户端之间行通信。服务器和客户端的具体流程 下方的信号都是系统提供的,我们只需要写相应的槽函数 A、服务器: 创建QTcpServer对象启动服务器(监听&…...

编译选项与常用环境变量
一、编译选项与常用环境变量 1、命令选项 -D 相当于就是定义,-D 可以理解为告诉cmake 后边我要定义一些参数,每定义一个就在前边加上-D就可以了,示例: #!/bin/shcmake -DTEST_DEBUGON . cmake --build .2、编译选项 下面列出来的…...
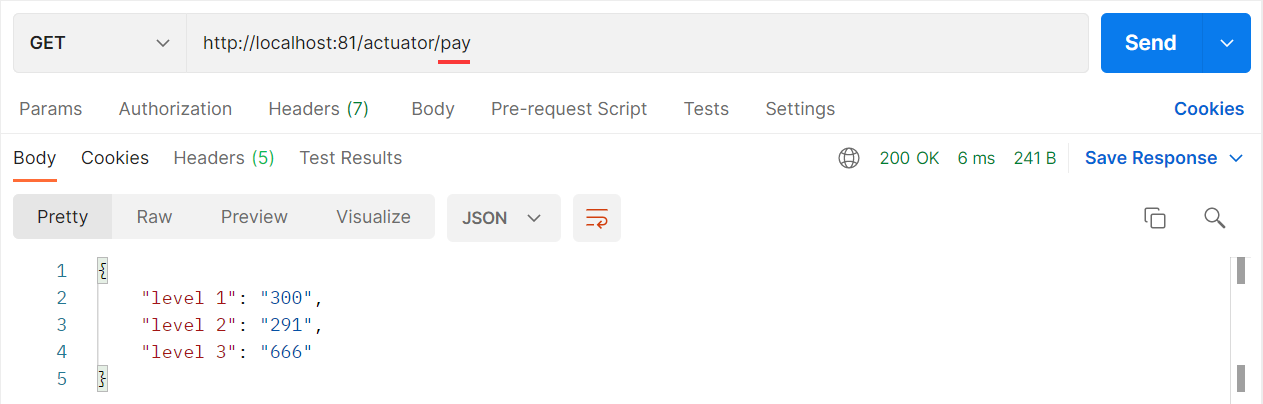
【SpringBoot2】SpringBoot开发实用篇
SpringBoot开发实用篇 KF-1.热部署 什么是热部署?简单说就是你程序改了,现在要重新启动服务器,嫌麻烦?不用重启,服务器会自己悄悄的把更新后的程序给重新加载一遍,这就是热部署。 热部署的功能是如…...

接口自动化测试框架搭建全部过程
思想: 1、基本目录的搭建 report:静态输出目录(报告或者日志) data:静态输入目录(可以存放Excel数据,被读取的一些数据) utils:实用方法层(这里存放的是项目的公共方法,一般拿到别…...
--DML_多表查询(针对数据表记录的join查询、子查询的操作))
SQL学习(十)--DML_多表查询(针对数据表记录的join查询、子查询的操作)
目录 1. 多表查询 -- 内连接查询 1.1 显示内连接 1.2 隐式内连接 2. 多表连接 -- 外连接查询...

Docker容器部署
Docker容器部署 为什么使用Docker什么是Docker类比用途 Docker基于Windows集成IDEA在window上安装docker设置Docker配置IDEA连接Docker测试启动SpringBoot应用测试 Docker基于Linux集成IDEA连接宿主机redis服务连接Docker中redis服务 为什么使用Docker 在和前端联调的过程中&a…...

26岁转行网络安全,成功上岸安全开发!
前言 我是去年 9 月 22 日才正式学习网络安全的,之前在国营单位工作了 4 年,在长沙一个月工资只有 5000 块,而且看不到任何晋升的希望,如果想要往上走,那背后就一定要有关系才行。 而且国营单位的气氛是你干的多了&a…...

涨点技巧: 谷歌强势推出优化器Lion,引入到Yolov8,内存更小、效率更高,秒杀Adam(W)
1.Lion优化器介绍 论文:https://arxiv.org/abs/2302.06675 代码:automl/lion at master google/automl GitHub 1.1 简单、内存高效、运行速度更快 1)与 AdamW 和各种自适应优化器需要同时保存一阶和二阶矩相比,Lion 只需要动量,将额外的内存占用减半; 2)由于 Lion…...

5年测试经验,自动化都不会?月薪11K都难拿....
我接触了太多测试同行,由于多数同行之前一直做手工测试,现在很迫切希望做自动化测试,其中不乏工作5年以上的同行。 我从事软件自动化测试已经近十年,接触过底层服务端、API 、Web、APP、H5 等等,对自动化算是比较了解…...
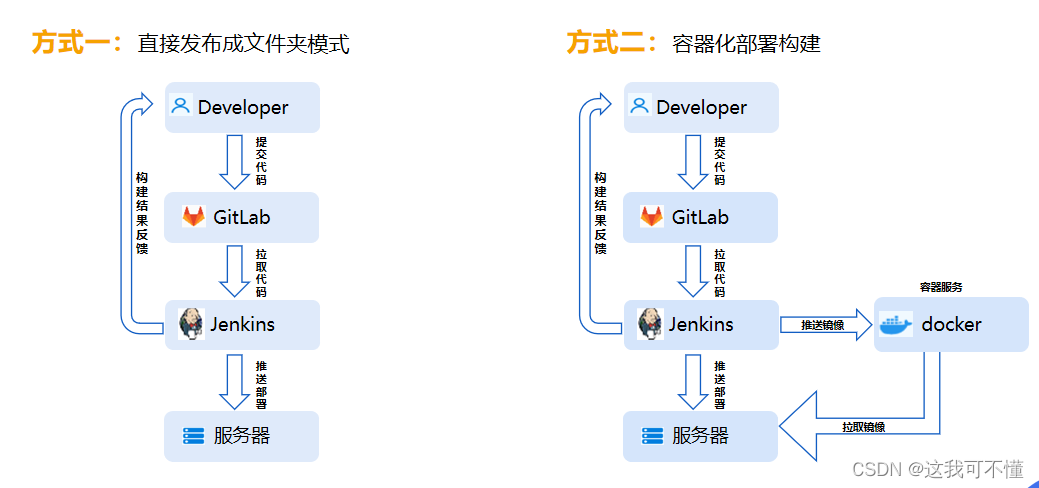
低代码平台名声臭,用起来却真香——60%开发者不敢承认
群体盲从意识会淹没个体的理性,个体一旦将自己归入该群体,其原本独立的理性就会被群体的无知疯狂所淹没。——《乌合之众》 不知道从什么时候开始,“低代码不行”的论调充斥着整个互联网圈子,csdn、掘金、知乎、B站、脉脉……到处…...
)
PHP 的代码简洁之道(Clean Code PHP)
介绍 Robert C.Martin’s 的 软件工程师准则 Clean Code 同样适用于 PHP。它并不是一个编码风格指南,它指导我们用 PHP 写出具有可读性,可复用性且可分解的代码。 并非所有的准则都必须严格遵守,甚至一些已经成为普遍的约定。这仅仅作为指导方…...

delphi在两个窗口间用消息通讯
用SendMessage在窗口间通讯: 发送方 var HWD: THandle; str1,str2:string; sData: TCopyDataStruct; begin HWD:FindWindow(nil,pchar(aaaaaa)); // Integer(pchar(self.Edit2.Text)) str2:我来了中玉人; str1:我来了中玉人; sData.cbDa…...
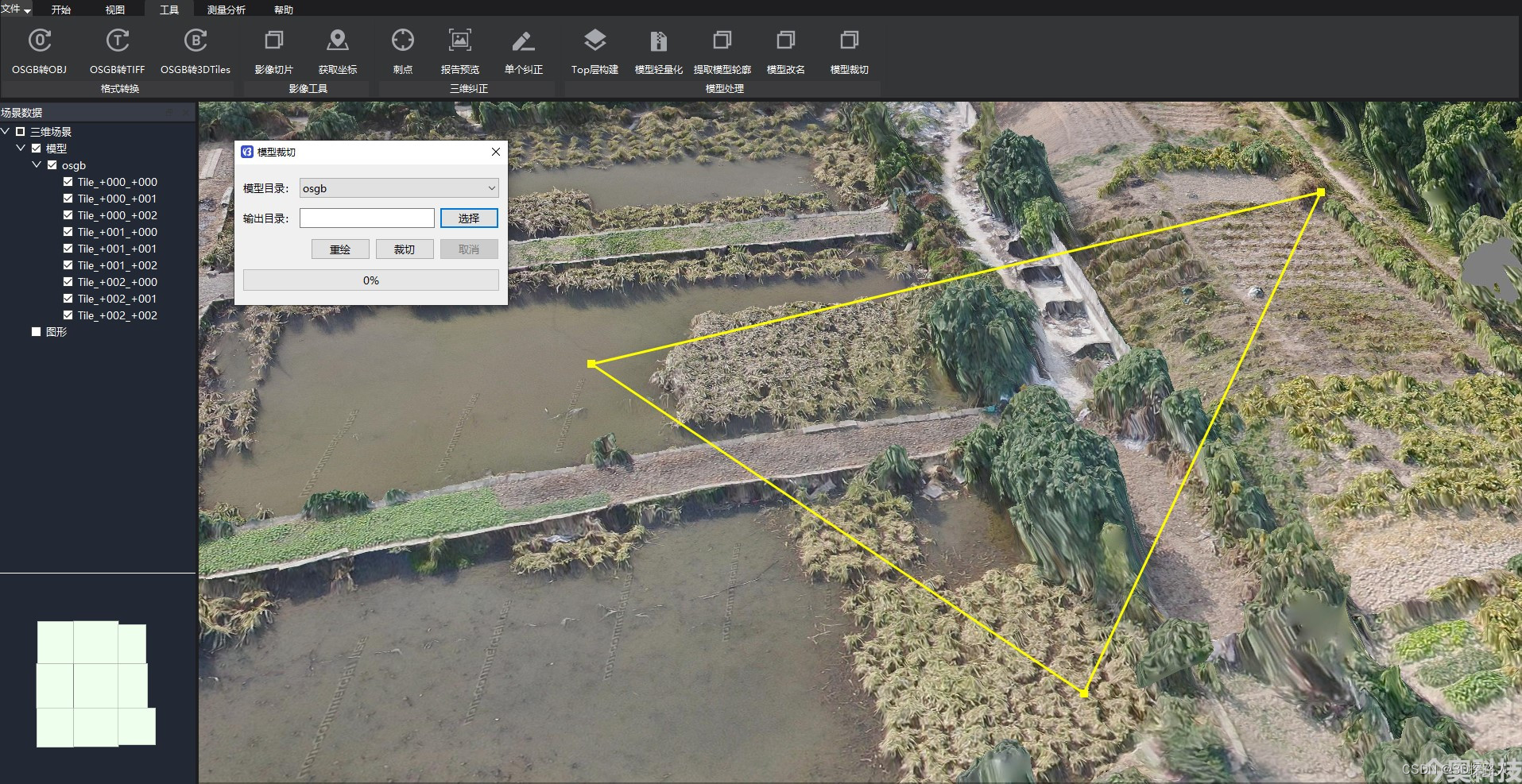
如何高效提高倾斜摄影三维模型顶层合并的技术方法分析
如何高效提高倾斜摄影三维模型顶层合并的技术方法分析 1、倾斜摄影三维模型顶层合并 1.1倾斜摄影三维模型是一种基于倾斜摄影技术,通过多个角度拍摄同一区域的影像,利用计算机图像处理和三维重建技术生成的三维地理信息数据。由于一个大区域可能需要多块…...
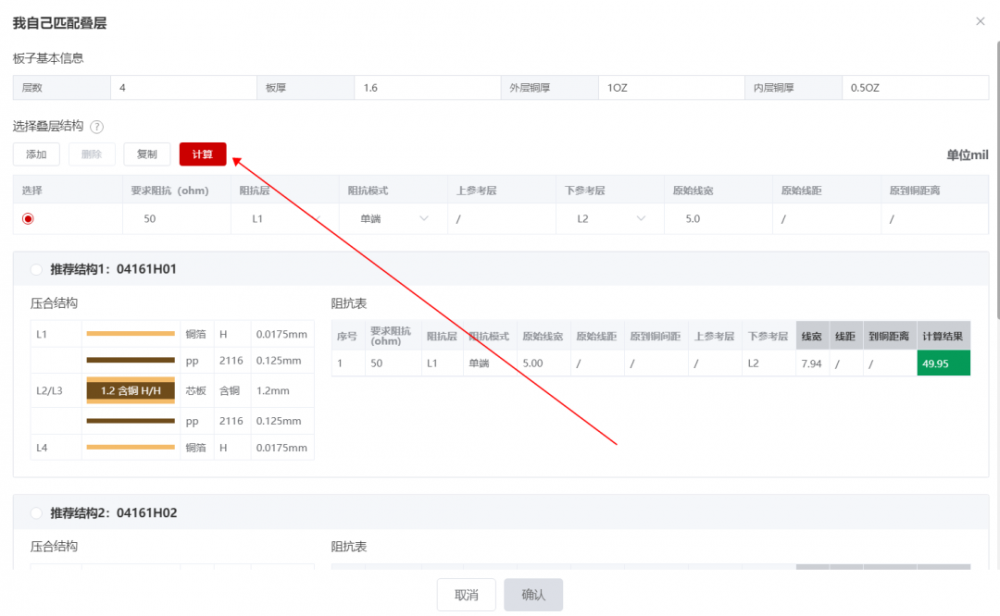
【科普】PCB为什么常用50Ω阻抗?6大原因
在PCB设计中,阻抗通常是指传输线的特性阻抗,这是电磁波在导线中传输时的特性阻抗,与导线的几何形状、介质材料和导线周围环境等因素有关。 对于一般的高速数字信号传输和RF电路,50Ω是一个常用的阻抗值。 为什么是50Ω?…...

Linux嵌入式uboot使用tftp网络启动加载zImage、设备树
文章目录 一、前言二、Linux U-boot 相关命令(1)help 命令(2)printenv 命令(3)setenv 函数(4)saveenv 函数 三、tftp启动linux内核步骤(1)进入u-boot模式&…...

使用Serv-U搭建FTP服务器并公网访问【内网穿透】
文章目录 1. 前言2. 本地FTP搭建2.1 Serv-U下载和安装2.2 Serv-U共享网页测试2.3 Cpolar下载和安装 3. 本地FTP发布3.1 Cpolar云端设置3.2 Cpolar本地设置 4. 公网访问测试5. 结语 1. 前言 科技日益发展的今天,移动电子设备似乎成了我们生活的主角,智能…...
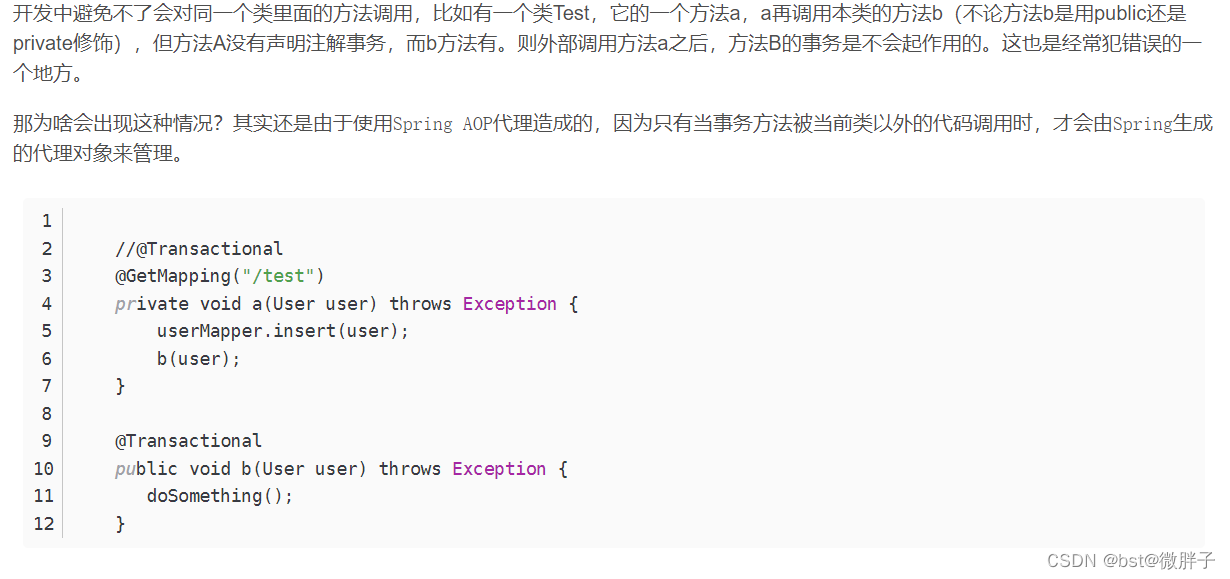
后端大厂面试总结大全六
目录: 1、Transactional注解控制事务有哪些不生效的场景2、MySQL的优化 1、Transactional注解控制事务有哪些不生效的场景 数据库引擎不支持事务数据源没有配置事务管理器没有被spring管理方法不是public的同一个类中方法调用,导致Transactional失效 举…...

2023五一数学建模A题B题C题思路模型代码
占个位置吧,开始在本帖实时更新五一数学建模赛题思路代码,文章末尾获取! 持续为更新参考思路 赛题思路 会持续进行思路模型分析,下自行获取。 A题思路: (比赛开始后第一时间更新) B题思路…...
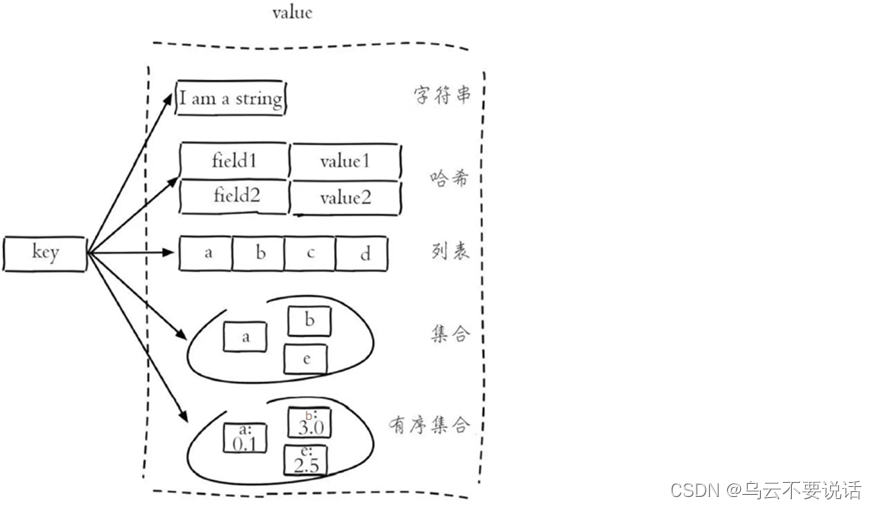
Redis --- 入门、数据类型
一、前言 1.1、什么是Redis Redis是一个基于内存的key-value结构数据库。Redis 是互联网技术领域使用最为广泛的存储中间件,它是「Remote Dictionary Service」的首字母缩写,也就是「远程字典服务」。 基于内存存储,读写性能高适合存储热点…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

