David Silver Reinforcement Learning -- Markov process
1 Introduction
这个章节介绍关键的理论概念。
马尔科夫过程的作用:
1)马尔科夫过程描述强化学习环境的方法,环境是完全能观测的;
2)几乎所有的RL问题可以转换成MDP的形式;
2 Markov Processes
2.1 Markov 属性
属性1:未来和过去无关,只受当前的状态影响
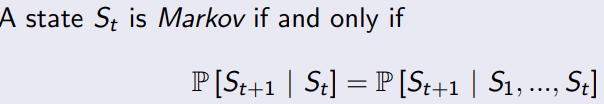
2.2 转移概率矩阵
从当前状态S转移到S’状态的概率,每行的概率之和为1.
2.3 markov chains
马尔科夫过程是无记忆的随机过程,一串状态以及markov的属性。一个马尔科夫过程,只要有有限个状态,以及他们之间相互转换的概率,就可以构建。

课程上给出了一个例子:
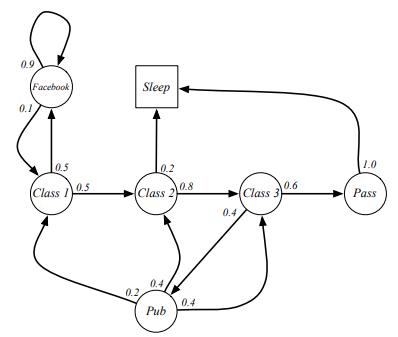
对应的转移概率矩阵

从class1 到 sleep有很多的链条

3 markov decision process
3.1 定义
马尔科夫奖励过程就是markov链和每个状态的reward
在马尔可夫决策过程(Markov Decision Process, MDP)中,奖励函数(reward function)是一个用于表示智能体在执行某个动作后所获得的即时奖励的函数。奖励函数通常用于指导智能体的行为,使其学会在面对不同的状态时做出对其最有利的决策。

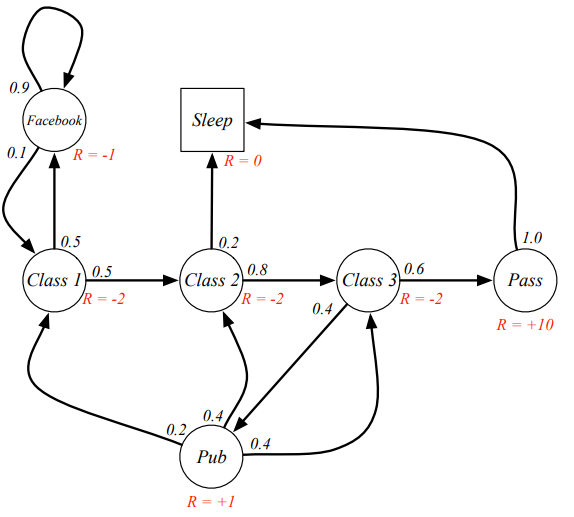
3.2 return
从时刻t开始的总折扣奖励是Gt。这里的折扣奖励是指将未来的奖励按照一定的比例进行打折,以体现当前奖励的价值。通过调整 γ \gamma γ调整未来reward的权重。
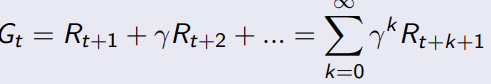
通过这个公式,可以算出来,从当前C1到最后SLEEP这个链的reward,比如可以用来选择走那条路径更优。

为什么要对后续的reward的添加权重
1.添加权重计算上比较简单;
2.避免循环马尔科夫链出现无穷大的情况
3.倾向于对眼前的利益
4.有时候也可能出现权重不衰减的情况;
3.3 value function
本质上还是用来评价当前这个状态好不好的,如何去评价,从当前状态到最终状态,可以积多少分
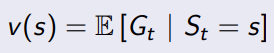
最简单的情况, γ = 0 \gamma=0 γ=0,完全不考虑未来
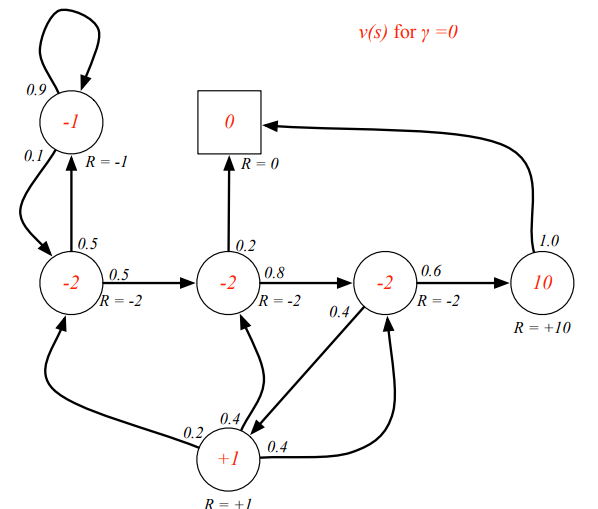
求一下S1 = C1, γ = 0.5 \gamma=0.5 γ=0.5的value值
问题:从S1=C1到最终的Sleep有很多条路径,那就有很多个结果,因为有状态概率矩阵,所以可以得到一个期望值?
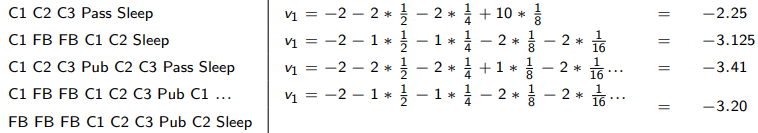
value function 必然选择最好的一条路径作为评价当前state的数值,这是一个典型的动态规划问题。
动态规划问题的思路就是将问题拆成更小的问题,当前 S t S_t St的value function不知道,但是只要知道 S t + 1 S_{t+1} St+1的状态,很容易得到当前时刻的value function。
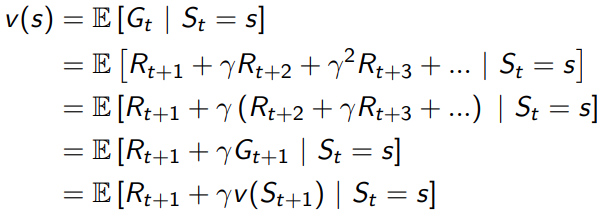
用图表示就是这个样子的
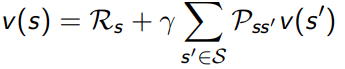
用动态规划的方法进行求解,且 γ = 1 \gamma=1 γ=1,得到一下的markov 状态的value function.
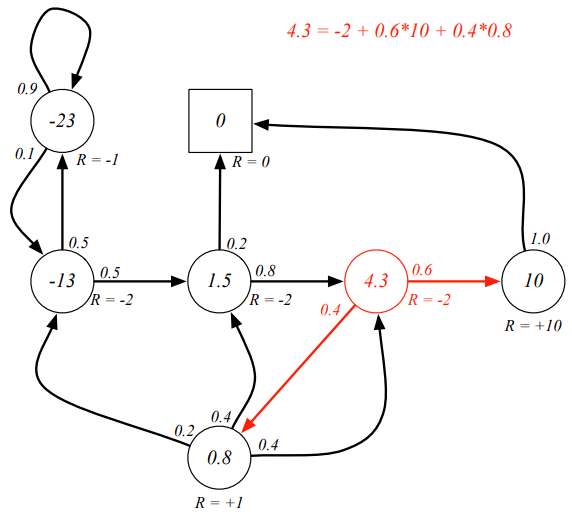
用矩阵的形式进行求解,
v = R + γ ∗ P ∗ v v = ( I − γ ∗ P ) − 1 R \begin{aligned} v &= R + \gamma * P* v \\ v &= (I - \gamma *P)^{-1}R \end{aligned} vv=R+γ∗P∗v=(I−γ∗P)−1R
验算一下上面的结果,因为$ (I - \gamma *P)$不可逆,比较悲剧,和上面这个结果差距很大,所以只能用其他方法来进行计算
,用value iteration的方法进行求解,因为我们这个问题维度比较小,只要最终状态收敛了就行。
function state_value = valueIterator(transition_matrix, reward_vector, discount_factor, tolerance)n = size(transition_matrix, 1);state_value = zeros(n, 1);delta = inf;while delta > tolerancenew_state_value = reward_vector + discount_factor * transition_matrix * state_value;delta = max(abs(new_state_value - state_value));state_value = new_state_value;end
end
求解结果: -12.5432, 1.4568, 4.3210, 10.0000, 0.8025, -22.5432, 0
1)动态规划,对于我们这个问题,可以尝试用动态规划
2)monte-carlo evaluation
3) temporal difference learning
4 Markov decision processes
马尔科夫奖励过程上再加上决策;

从S到S’,是因为有action的推动。
问题:既然有action主动的去推动,还需要状态转移概率矩阵吗?
一种理解方式:处于当前状态S,有 P s s ′ a P^a_{ss'} Pss′a的概率去执行动作a;
4.1 policies
在马尔可夫决策过程(MDP)的环境中,策略是一个从状态到动作的映射,表示代理(Agent)在每个状态下选择采取哪个动作的规则。通常用π表示策略,即π(a|s)表示在状态s下采取动作a的概率

再来理解一下状态转移矩阵和policy矩阵的区别
状态转移矩阵(Transition Matrix):它表示在给定状态下执行某个动作后到达下一个状态的概率。状态转移矩阵的元素P(s’|s, a)表示在状态s下执行动作a,然后到达状态s’的概率。状态转移矩阵是MDP中一个固定的特性,与策略无关。它描述了在执行一个动作后,环境如何变化。
策略(Policy)矩阵:它表示在给定状态下选择执行某个动作的概率。策略矩阵的元素π(a|s)表示在状态s下选择执行动作a的概率。策略矩阵是MDP中的一个可调整的特性,可以根据需要选择不同的策略。它描述了在给定状态下,智能体如何选择执行动作。
考虑policy之后,从状态s到状态s’,要先经过一个状态概率输出动作a,然后再由 P s s ′ a P_{ss'}^a Pss′a的状态转移矩阵过去。
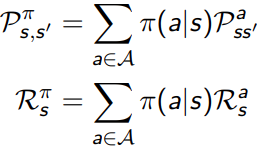
书中给的这两个关系,不太能理解
4.2 Value functions
4.2.1 state-value function
状态之间的转移如今不是单纯的确定概率了,而且可以通过策略进行调整了,在新策略之下,衡量当前S的状态评分。
状态价值函数 V(s):在状态 s 下遵循策略π的预期回报。即在状态 s 下,智能体采取策略π所能获得的长期回报的期望值。
使用公式进行计算,
V π ( s ) = ∑ a ∈ A π ( a ∣ s ) [ R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V π ( s ′ ) ] V_{\pi}(s) = \sum_{a \in \mathcal{A}} \pi(a|s) \left[R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P(s'|s, a) V_{\pi}(s')\right] Vπ(s)=a∈A∑π(a∣s)[R(s,a)+γs′∈S∑P(s′∣s,a)Vπ(s′)]
从用下图去表示,
转换成矩阵形式, v π ( s ) v_{\pi}(s) vπ(s)是一个
找一个简单的问题:
假设一个机器人处于一个4x4的网格世界,每个网格代表一个状态,共有16个状态(S1至S16)。机器人可以采取四个动作:上(U)、下(D)、左(L)和右(R)。假设机器人在状态S1(左上角),试图向右移动。然而,由于地面湿滑,机器人执行动作的不确定性使得实际移动方向可能发生偏移。
在这个例子中,当机器人试图从状态S1向右移动时,实际状态转移概率分布可能如下:
转移到状态S2(向右)的概率:0.8
转移到状态S5(向下)的概率:0.2
我们用一个4x4x4的张量来表示状态转移矩阵,第一维表示动作(上、下、左、右),第二维表示起始状态,第三维表示目标状态。这里我们仅提供一个概要的状态转移矩阵,仅包含部分非零元素
% 参数设置
num_states = 16;
num_actions = 4;
gamma = 0.9; % 折扣因子
theta = 1e-6; % 阈值,用于判断价值函数收敛
max_iter = 1000; % 最大迭代次数% 状态转移矩阵 (4x16x16,对应于动作的顺序是:上、下、左、右)
P = zeros(num_actions, num_states, num_states);% 定义状态转移矩阵的函数
% 省略了具体的状态转移矩阵实现,您可以根据之前的讨论来定义状态转移矩阵% 奖励函数(16x4,行表示状态,列表示动作)
% 您可以根据实际问题自定义奖励函数
R = ...;% 策略(16x4,行表示状态,列表示动作),均匀随机策略
policy = ones(num_states, num_actions) / num_actions;% 初始化状态价值函数(1x16)
V = zeros(1, num_states);% 迭代计算状态价值函数
for iter = 1:max_iterV_old = V;for s = 1:num_statesV_temp = 0;for a = 1:num_actionsV_temp = V_temp + policy(s, a) * (R(s, a) + gamma * sum(P(a, s, :) .* V_old));endV(s) = V_temp;end% 判断价值函数是否收敛if max(abs(V - V_old)) < thetabreak;end
end% 输出状态价值函数
disp(V);
4.2.2 action value function
用于评估在给定策略下,一个状态下采取某个动作的长期价值。它表示从当前状态开始,首先执行某一特定动作,然后遵循给定策略,预期累计奖励的期望值。用Q(s, a)表示动作价值函数,其中s为状态,a为动作,Q(s, a)为在状态s下执行动作a的动作价值。
动作价值函数的意义在于,它可以帮助智能体在给定状态下选择最优的动作。通过比较不同动作的动作价值函数,智能体可以选择具有最高长期价值的动作,从而实现策略的优化。
为了选择最优的动作,智能体可以比较这些动作的动作价值函数Q(s, a),并选择具有最高价值的动作。例如,如果在当前位置,向右移动的动作价值函数Q(s, 右)最高,智能体将选择向右移动,以期望获得最大的累计奖励。
总之,状态价值函数V(s)用于评估在给定策略下,一个状态的长期价值;动作价值函数Q(s, a)用于评估在给定策略下,一个状态下采取某个动作的长期价值。动作价值函数对智能体具有重要意义,因为它可以帮助智能体在给定状态下选择最优的动作,从而实现策略的优化。
用action value function的定义就能看出,跟后续的状态的state value是相关的,接下来推导他们的关系。
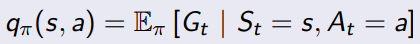
从公式来看,执行一连串的
Q π ( s , a ) = R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V π ( s ′ ) Q^{\pi}(s, a) = R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V^{\pi}(s') Qπ(s,a)=R(s,a)+γs′∈S∑P(s′∣s,a)Vπ(s′)
这个公式很容易理解,
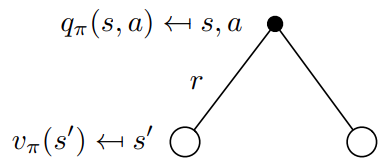
4.2.3 用bellman function 总结上面的关系
V π ( s ) = ∑ a ∈ A π ( a ∣ s ) [ R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V π ( s ′ ) ] R π ( s ) = ∑ a ∈ A π ( a ∣ s ) R ( s , a ) P π ( s ′ ∣ s ) = ∑ a ∈ A ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V π ( s ) = R π ( s ) + γ P π ( s ′ ∣ s ) V π ( s ) \begin{aligned} V_{\pi}(s) &= \sum_{a \in \mathcal{A}} \pi(a|s) \left[R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P(s'|s, a) V_{\pi}(s')\right] \\ R^{\pi} (s)& = \sum_{a \in \mathcal{A}} \pi(a|s) R(s, a) \\ P^{\pi}(s'|s) & = \sum_{a \in \mathcal{A}} \sum_{s' \in \mathcal{S}} P(s'|s, a) \\ V_{\pi}(s) & = R^{\pi}(s)+\gamma P^{\pi}(s'|s) V_{\pi}(s) \end{aligned} Vπ(s)Rπ(s)Pπ(s′∣s)Vπ(s)=a∈A∑π(a∣s)[R(s,a)+γs′∈S∑P(s′∣s,a)Vπ(s′)]=a∈A∑π(a∣s)R(s,a)=a∈A∑s′∈S∑P(s′∣s,a)=Rπ(s)+γPπ(s′∣s)Vπ(s)
看一下带policy的reward的应该如何定义,R(s,a)表示处于状态s情况下,采用动作a的奖励,
R π R^{\pi} Rπ表示在给定策略π下,智能体在状态s采取不同动作a的期望奖励。
4.3 optimal value functions
4.3.1 optimal state value function
找一个最好的policy去最大化状态value function
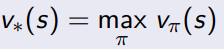
找一个最好的policy去最大化action value function
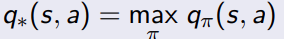
定义什么是最优的policy
所有的state, 取得了最大的value function
所有的action,取得了最大的action value 数值
4.3.2 如何寻找optimal policy
简单理解就是要最大化action value的期望。
要确定全局的最优策略,我们需要关注的是状态-动作价值函数(state-action value function),也被称为Q-function。Q-function 衡量了在特定策略下,从某一状态(state)采取某一动作(action)开始所能获得的期望累积奖励。我们可以使用贝尔曼最优方程(Bellman optimality equation)来寻找最优策略。
再来回顾一下action value function的定义,
Q π ( s , a ) = R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V π ( s ′ ) V π ( s ) = ∑ a ∈ A π ( a ∣ s ) [ R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V π ( s ′ ) ] Q ∗ ( s , a ) = R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V ∗ ( s ′ ) V ∗ ( s ) = max a ( R ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V ∗ ( s ′ ) ) \begin{aligned} Q^{\pi}(s, a) &= R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V^{\pi}(s') \\ V_{\pi}(s) &= \sum_{a \in \mathcal{A}} \pi(a|s) \left[R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P(s'|s, a) V_{\pi}(s')\right]\\ Q^{*}(s, a) &= R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V^{*}(s') \\ V^*(s) & = \max_a \left( R(s, a) + \gamma \sum_{s'} P(s'|s, a) V^*(s') \right) \\ \end{aligned} Qπ(s,a)Vπ(s)Q∗(s,a)V∗(s)=R(s,a)+γs′∈S∑P(s′∣s,a)Vπ(s′)=a∈A∑π(a∣s)[R(s,a)+γs′∈S∑P(s′∣s,a)Vπ(s′)]=R(s,a)+γs′∈S∑P(s′∣s,a)V∗(s′)=amax(R(s,a)+γs′∑P(s′∣s,a)V∗(s′))
重要的公式1,optimal value function 和optimal action value function的关系
V ∗ ( s ) = max a Q ∗ ( s , a ) V^*(s) = \max_a Q^*(s, a) V∗(s)=amaxQ∗(s,a)
它表示在状态 s s s下,最优状态价值函数 V ∗ ( s ) V^*(s) V∗(s)等于所有可能动作的最优状态-动作价值函数 Q ∗ ( s , a ) Q^*(s, a) Q∗(s,a)的最大值。换句话说,如果我们遵循最优策略,在状态 s s s下,我们会选择那个能让我们获得最大期望累积奖励的动作。
从理解的角度, state的value和最优的action的结果相同,
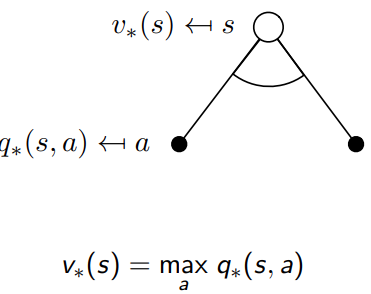
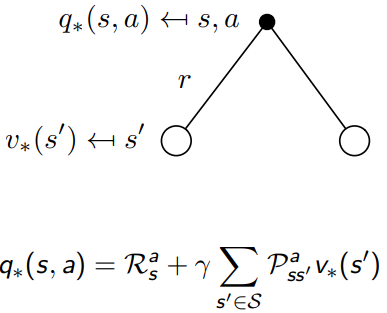
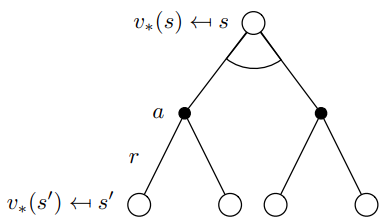
重要的公式2,optimal value function 和optimal action value function的关系
Q ∗ ( s , a ) = R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V ∗ ( s ′ ) V ∗ ( s ) = max a ( R ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V ∗ ( s ′ ) ) \begin{aligned} Q^{*}(s, a) &= R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V^{*}(s') \\ V^*(s) & = \max_a \left( R(s, a) + \gamma \sum_{s'} P(s'|s, a) V^*(s') \right) \\ \end{aligned} Q∗(s,a)V∗(s)=R(s,a)+γs′∈S∑P(s′∣s,a)V∗(s′)=amax(R(s,a)+γs′∑P(s′∣s,a)V∗(s′))
Q ∗ ( s , a ) = R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V ∗ ( s ′ ) Q ∗ ( s , a ) = R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) max a ′ q ∗ ( s ′ , a ′ ) \begin{aligned} Q^{*}(s, a) &= R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V^{*}(s') \\ Q^{*}(s, a) &= R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) \max_{a'} q^*(s',a') \end{aligned} Q∗(s,a)Q∗(s,a)=R(s,a)+γs′∈S∑P(s′∣s,a)V∗(s′)=R(s,a)+γs′∈S∑P(s′∣s,a)a′maxq∗(s′,a′)
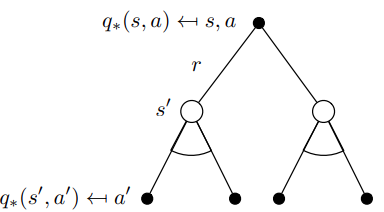
求解的办法
1)value iteration
2) Policy iteration
3) Q-learning
4) Sarsa
5 Extensions to MDPs
5.1 infinite and continuous mdps
- Countably infinite state and/or action spaces
- Straightforward
- Continuous state and/or action spaces
- closed form for linear quadratic model
- continuous time
- 需要微分动态方程
- HJB 方程
- limiting case of Bellman equation as time-step
5.2 Partially observable MDPs

5.2.1 belief states
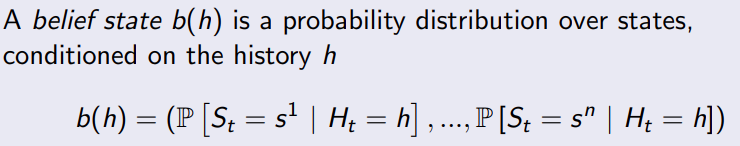
5.3 Undiscounted, average reward MDP
相关文章:
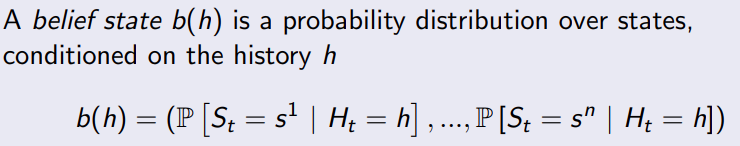
David Silver Reinforcement Learning -- Markov process
1 Introduction 这个章节介绍关键的理论概念。 马尔科夫过程的作用: 1)马尔科夫过程描述强化学习环境的方法,环境是完全能观测的; 2)几乎所有的RL问题可以转换成MDP的形式; 2 Markov Processes 2.1 Mark…...
项目结束倒数2
今天,解决了,多个点的最短路问题 用的dfs,配上了floyed计算出的广源距离 难点是要记录路线,dfs记录路线就很烦 但是好在结束了,经过无数的测试,确保没啥问题(应该把) 来看看我的代码 void dfs(int b[], int x, int* sum, int last, int sums, int a[], BFS& s, Floyd_A…...
VBA智慧办公9——图例控件教程
如图,利用VBA进行可视化交互界面的设计,在界面中我们用到了label,button,text,title等多个工具,在进行框图效果的逐一实现后可进行相应的操作和效果实现。 VBA(Visual Basic for Applications&a…...

Presto VS Spark
环境配置 5个节点,每个节点10G内存。 测试SQL,每个执行3次,求平均,对比计算性能。 版本信息 Spark:2.3.1Presto: 0.208 10亿量级查询性能对别 Spark: spark-sql> select sex,count(1) from conta…...
为什么我们能判断声音的远近
想象一下,当我们走在路上时,听到了头顶的鸟儿在树梢间的叫声,即使无法透过浓密的树叶看见它,也可以大致知道鸟儿的距离。此时身后传来由远到近自行车铃铛声,我们并不需要回过头去看,便为它让开了道路。这些…...

那些关于DIP器件不得不说的坑
了解什么是DIP DIP就是插件,采用这种封装方式的芯片有两排引脚,可以直接焊在有DIP结构的芯片插座上或焊在有相同焊孔数的焊位中。其特点是可以很方便地实现PCB板的穿孔焊接,和主板有很好的兼容性,但是由于其封装面积和厚度都比较…...
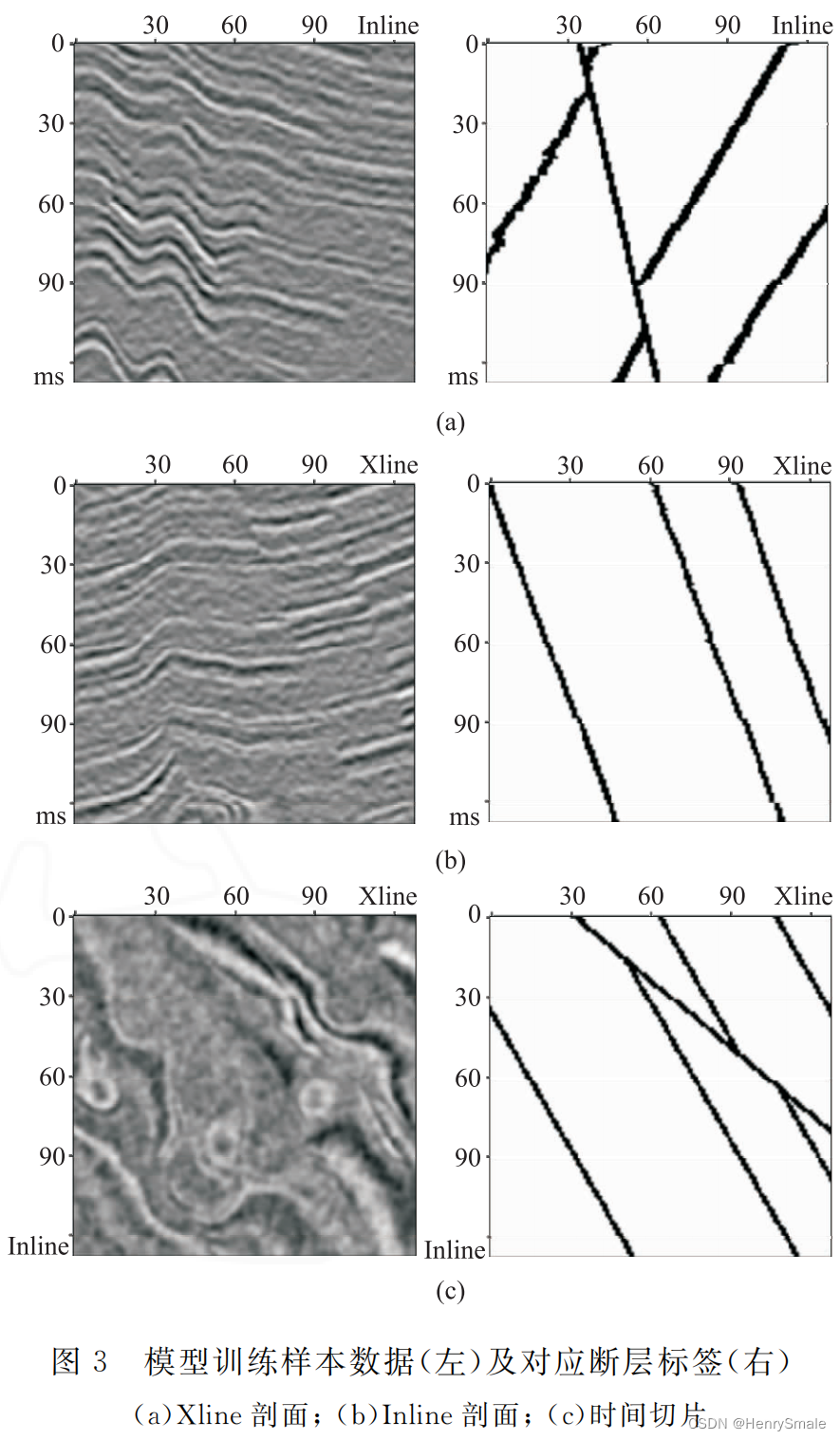
论文笔记:基于U-Net深度学习网络的地震数据断层检测
0 论文简介 论文:基于U-Net深度学习网络的地震数据断层检测 发表:2021年发表在石油地球物理勘探 1 问题分析和主要解决思路 问题:断层智能识别,就是如何利用人工智能技术识别出断层。 解决思路:结合U-N…...
kafka单节点快速搭建
1.搭建使用centos7主机,关闭防火墙和selinux服务 2.创建kafka存放目录 mkdir /etc/kafka 3.从kafka官网下载安装包 我这里下载了3.3.1版本的kafka,放到kafka目录中 下载地址:Apache Kafka 4.解压安装包并更改名称 tar -zxvf /etc/kaf…...
常用函数)
【MySQL】(6)常用函数
文章目录 日期函数获取日期日期计算 字符串函数charsetconcatlengthsubstringreplaceinstrstrcmpltrim, rtrim, trim 数学函数absbin, hexconvceiling, floorrandformatmod 其他函数user() 查询当前用户密码加密md5()password() database() 查看当前数据库ifnull() 日期函数 函…...

Linux学习 Day1
注意: 以下内容均为本人初学阶段学习的内容记录,所以不要指望当成查漏补缺的字典使用。 目录 1. ls指令 2. pwd指令 3. cd指令 4. touch指令 5. mkdir指令(重要) 6. rmdir指令 && rm 指令(重要ÿ…...

Hibernate中的一对多和多对多关系
Hibernate的一对多和多对多 Hibernate是一个优秀的ORM框架,它简化了Java应用程序与关系型数据库之间的数据访问。在Hibernate中,我们可以使用一对多和多对多的关系来处理复杂的数据模型。本文将介绍Hibernate中的一对多和多对多,包括配置和操…...
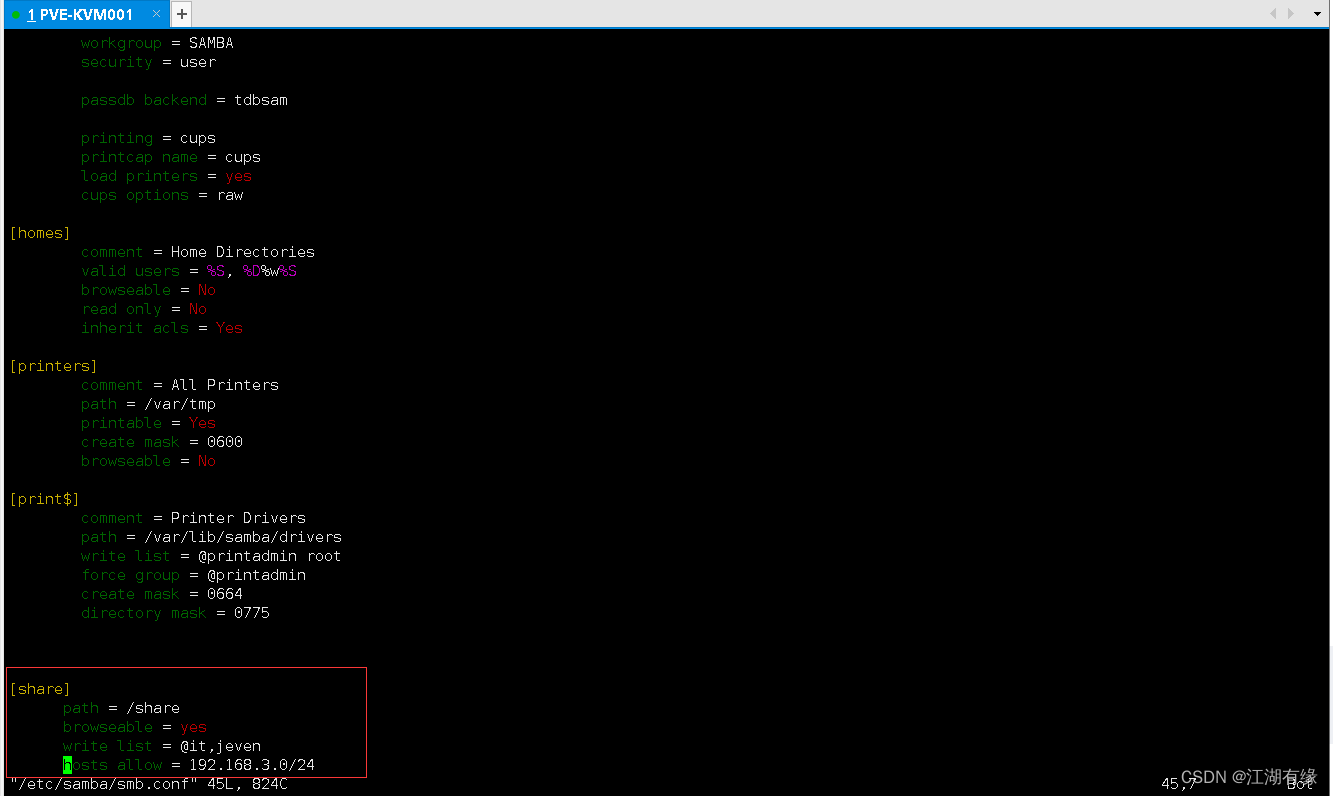
Linux系统之部署Samba服务
Linux系统之部署Samba服务 一、Samba服务介绍1.Samba服务简介2.NFS和CIFS简介3.Smaba服务相关包4.samba监听端口4.samba相关工具及命令 二、环境规划介绍1.环境规划2.本次实践介绍 三、Samba服务端配置1.检查yum仓库2.安装smaba相关软件包3.创建共享目录4.设置共享目录权限5.新…...

回顾产业互联网的发展历程,技术的支撑是必不可少的
从以新零售、全真互联网为代表的产业互联网的概念诞生的那一天开始,互联网的玩家们就一直都在寻找着它们的下一站。尽管在这个过程当中,遭遇到了很多的困难,走过了很多的弯路,但是,产业互联网的大方向,却始…...

关于gas费优化问题
关于gas费优化问题 首先我们先来看一下这段代码 // SPDX-License-Identifier: MIT pragma solidity ^0.8.0; contract GasGolf{uint public total;//[1,2,3,4,5,100]function sum(uint[] memory nums) external{for(uint i 0;i<nums.length;i1){bool isEven nums[i] % 2…...
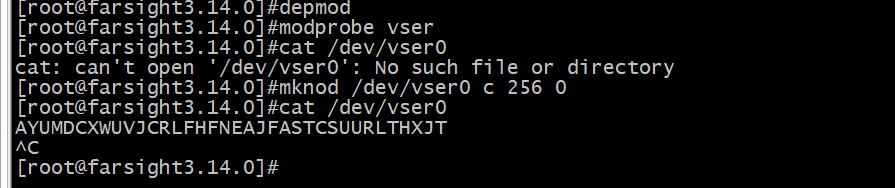
Linux——中断和时间管理(中)
目录 驱动中的中断处理 中断下半部 软中断 tasklet 工作队列 驱动中的中断处理 通过上一节的分析不难发现,要在驱动中支持中断,则需要构造一个 struct irqaction的结构对象,并根据IRQ 号加入到对应的链表中(因为 irq_des 已经在内核初始…...

嵌入式软件中常见的 8 种数据结构详解
目录 第一:数组 1、数组的应用 第二:链表 1、链表操作 2、链表的应用 第三:堆栈 1、堆栈操作 2、堆栈的应用 第四:队列 1、队列操作 2、队列的应用 第五:哈希表 1、哈希函数 2、哈希表的应用 第六&#…...

vue 修改当前路由参数并刷新界面
项目中经常用到的需求是在当前页面修改路由中的参数,并刷新页面。 我们只用this. r o u t e r . r e p l a c e 或者 t h i s . router.replace或者this. router.replace或者this.router.go是不行的,需配合下面的代码 方法一: this.$router.…...

视频处理之视频抽帧的python脚本
在计算机视觉研究中,处理视频的时候,往往需要将视频抽帧成图片。如果多个视频都存放在一个文件夹里,并且希望抽帧出来的图片,以一个视频对应一个文件夹的形式存放,可以用以下代码,抽帧频率可自己手动修改&a…...

【youcans 的 OpenCV 学习课】22. Haar 级联分类器
专栏地址:『youcans 的图像处理学习课』 文章目录:『youcans 的图像处理学习课 - 总目录』 【youcans 的 OpenCV 学习课】22. Haar 级联分类器 3. Haar 特征及其加速计算3.1 Haar 特征3.2 Haar 特征值的计算3.3 积分图像3.4 基于积分图像加速计算 Haar 特…...

如何避免知识盲区 《人生处处是修行》 读书笔记
如何避免知识盲区 多元化学习:不要只关注自己擅长的领域,应该尝试学习其他领域的知识,例如文学、艺术、科学等。 拓宽阅读:阅读不同领域的书籍、文章、博客等,可以帮助你了解更多的知识和观点。 参加培训和课程&…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...