代码随想录算法训练营第四十三天
代码随想录算法训练营第四十三天| 1049. 最后一块石头的重量 II,494. 目标和,474. 一和零
- 1049. 最后一块石头的重量 II
- 494. 目标和
- 474. 一和零
1049. 最后一块石头的重量 II
题目链接:最后一块石头的重量 II
重点:
本题其实就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小
和 416. 分割等和子集比较相似
0-1背包要素:
- 背包体积:sum//2
- 物品价值:stones[i]
- 物品重量:stones[i]
- 物品可以用一次
动态规划要素:
- dp[i][j] = [0,i]任选石头在背包容量为j的前提下可以达到的最大体积。
- 之后的都和经典0-1问题一样
class Solution:def lastStoneWeightII(self, stones: List[int]) -> int:# dp[i][j] = [0,i]任选石头在背包容量为j的前提下可以达到的最大体积。target = sum(stones)//2dp = [[0]*(target+1) for _ in range(len(stones))]# 初始化for j in range(target+1):if stones[0] <= j:dp[0][j] = stones[0]for i in range(1,len(stones)):for j in range(1,(target+1)):if stones[i] > j: # 放不进去,就用i之前的元素dp[i][j] = dp[i-1][j]else:dp[i][j] = max(dp[i-1][j], dp[i-1][j-stones[i]]+stones[i])#print(dp[-1][-1])return abs(2*dp[-1][-1]-sum(stones))
一维:
dp[j] = 在背包容量为j的前提下可以达到的最大体积。
class Solution:def lastStoneWeightII(self, stones: List[int]) -> int:# dp[j] = 任选石头在背包容量为j的前提下可以达到的最大体积。target = sum(stones)//2dp = [0]*(target+1)for i in range(len(stones)):for j in range(target,0,-1):if stones[i] <= j:dp[j] = max(dp[j],dp[j-stones[i]]+stones[i])return abs(2*dp[-1]-sum(stones))
494. 目标和
题目链接:目标和
- dp[i][j] = [0,i]任选元素可以达到
j-t的不同表达数目 - 由于只能加减,范围是
-sum(nums)到sum(nums) - 初始化:dp的第一行,只有一个元素,所以-i或者i等于j代表的和时,就加一
- 递推公式:每次多加一个元素可以
+nums[i]或者-nums[i],所有如果之前的元素可以组成j-t+nums[i]或者j-t-nums[i]的就可以达到j-t,也就是说在如果在dp下标范围内,dp[i][j]的次数就是j-t+nums[i]的次数加上j-t-nums[i]的次数。
先不降成一维了,自己都搞不清
class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:# dp[i][j] = [0,i]任选元素可以达到j的不同表达数目t = sum(nums)if target > t or target < -t:return 0dp = [[0]*(2*t+1) for _ in range(len(nums))]for j in range(2*t+1):if nums[0] == j-t:dp[0][j] += 1if -nums[0] == j-t:dp[0][j] += 1for i in range(1,len(nums)):for j in range(2*t+1):#print(j-target-nums[i],j-target+nums[i])if j-t-nums[i] >= -t and j-t+nums[i] <= t:#print(1)dp[i][j] += dp[i-1][j-nums[i]] + dp[i-1][j+nums[i]] elif j-t-nums[i] < -t and j-t+nums[i] <= t:#print(2)dp[i][j] += dp[i-1][j+nums[i]] elif j-t-nums[i] >= -t and j-t+nums[i] > t:#print(3)dp[i][j] += dp[i-1][j-nums[i]]return dp[-1][sum(nums)+target]
474. 一和零
题目链接:一和零
这个背包的重量是两维的需要满足0的数量和1的数量。为了不让dp变成三维的试一下之前的一维累加吧。
dp[i][j] = 拥有最多i个0和j个1的最长子集长度。
class Solution:def findMaxForm(self, strs: List[str], m: int, n: int) -> int:# dp[i][j] = 最多拥有i个0和j个1的最长子集长度。dp = [[0]*(m+1) for _ in range(n+1)]for i in range(len(strs)):one = strs[i].count('1')zero = strs[i].count('0')for j in range(n,-1,-1):for k in range(m,-1,-1):if one <= j and zero <= k:dp[j][k] = max(dp[j][k],dp[j-one][k-zero]+1)return dp[-1][-1]
相关文章:

代码随想录算法训练营第四十三天
代码随想录算法训练营第四十三天| 1049. 最后一块石头的重量 II,494. 目标和,474. 一和零 1049. 最后一块石头的重量 II494. 目标和474. 一和零 1049. 最后一块石头的重量 II 题目链接:最后一块石头的重量 II 重点: 本题其实就是…...
如何在 Mac 和 Windows 上恢复未保存或删除的 PDF
Adobe Acrobat PDF 是一种常用格式。我们可能会在不同的 PDF 编辑器中编辑和保存 PDF 文件。但是,如果不保存 PDF 文件或不小心将其删除,那将是一种令人不安的体验。 保持冷静!首先,尽可能多地停止运行应用程序,这样它…...

windows开机不自动挂载磁盘的方法
本人的电脑系统为win11 写作时间20230430 开机不挂载某块磁盘的理由 1.本人电脑上有个仓库盘是机械硬盘,并不是每次开机都要用到,开机不挂载也许有利于增加数据盘的寿命 2.挂载了数据盘,有时候打开文件页面会比较慢,不够丝滑 …...

5 款 AI 老照片修复工具的横向比较
在大语言模型和各类 AI 应用日新月异的今天,我终于下定决心,趁着老照片们还没有完全发黄褪色、受潮粘连抑或损坏遗失,将上一代人实体相册里的纸质胶卷照片全部数字化,并进行一次彻底的 AI 修复,好让这些珍贵的记忆能更…...

2023企业服务的关键词:做强平台底座
作者 | 曾响铃 文 | 响铃说 4月下旬,软件行业相关的大会紧锣密鼓地开了好几场,不仅有政府主办的2023中国国际软件发展大会、中国软件创新发展大会,也有用友、浪潮等服务商举办的品牌活动,让软件业的话题一直保持热度。 以用友为…...
【Linux基本指令和权限(1)】
本文思维导图: 文章目录 一、Linux操作的特点二、使用指令从Xhell登录云服务器三、基本指令1.ls指令2. pwd指令:3.cd指令4. touch指令5. rm指令 写在最后 Linux是一个操作系统,操作系统是一款做软硬件管理的软件。 一、Linux操作的特点 Li…...

虹科新品 | 用于医疗应用的压力和气体流量传感器
ES Systems在创新MEMS方面拥有丰富的经验,设计了高质量和高性能的气体流量和压力传感器,由于其技术规格,出色的可靠性和有竞争力的价格,这些传感器在竞争产品中具有独特的品质。 Part.01 应用背景 众所周知,在医疗领域…...
原生小程序如何使用pdf.js实现查看pdf,以及关键词检索高亮
1.下载pdf.js库文件 前往 pdf.js 的 官网 下载库文件,下哪个版本都可以,后者适用于旧版浏览器,所以我下载的是后者 下载完成后,因为微信小程序打包的限制,我将库文件放到项目的后台系统了,在h5端处理会比在…...

「数据架构」MDM实现失败的主要原因
我经常参与一个组织的MDM程序,当他们在一个失败的项目之后向InfoTrellis请求帮助进行清理,或者开始尝试X,以实现对某些人来说非常困难的目标时。主数据管理实现失败的原因有很多,但是没有一个是由于在这些场景中使用的责备游戏的原…...
【Java基础 1】Java 环境搭建
🍊 欢迎加入社区,寒冬更应该抱团学习:Java社区 📆 最近更新:2023年4月22日 文章目录 1 java发展史及特点1.1 发展史1.2 Java 特点1.2.1 可以做什么?1.2.2 特性 2 Java 跨平台原理2.1 两种核心机制2.2 JVM…...

2023-4-26-C++11新特性之正则表达式
🍿*★,*:.☆( ̄▽ ̄)/$:*.★* 🍿 💥💥💥欢迎来到🤞汤姆🤞的csdn博文💥💥💥 💟💟喜欢的朋友可以关注一下…...
python接口自动化测试 requests库的基础使用
目录 简单介绍 Get请求 Post请求 其他类型请求 自定义headers和cookies SSL 证书验证 响应内容 获取header 获取cookies 简单介绍 requests库简单易用的HTTP库 Get请求 格式: requests.get(url) 注意:若需要传请求参数,可直接在 …...
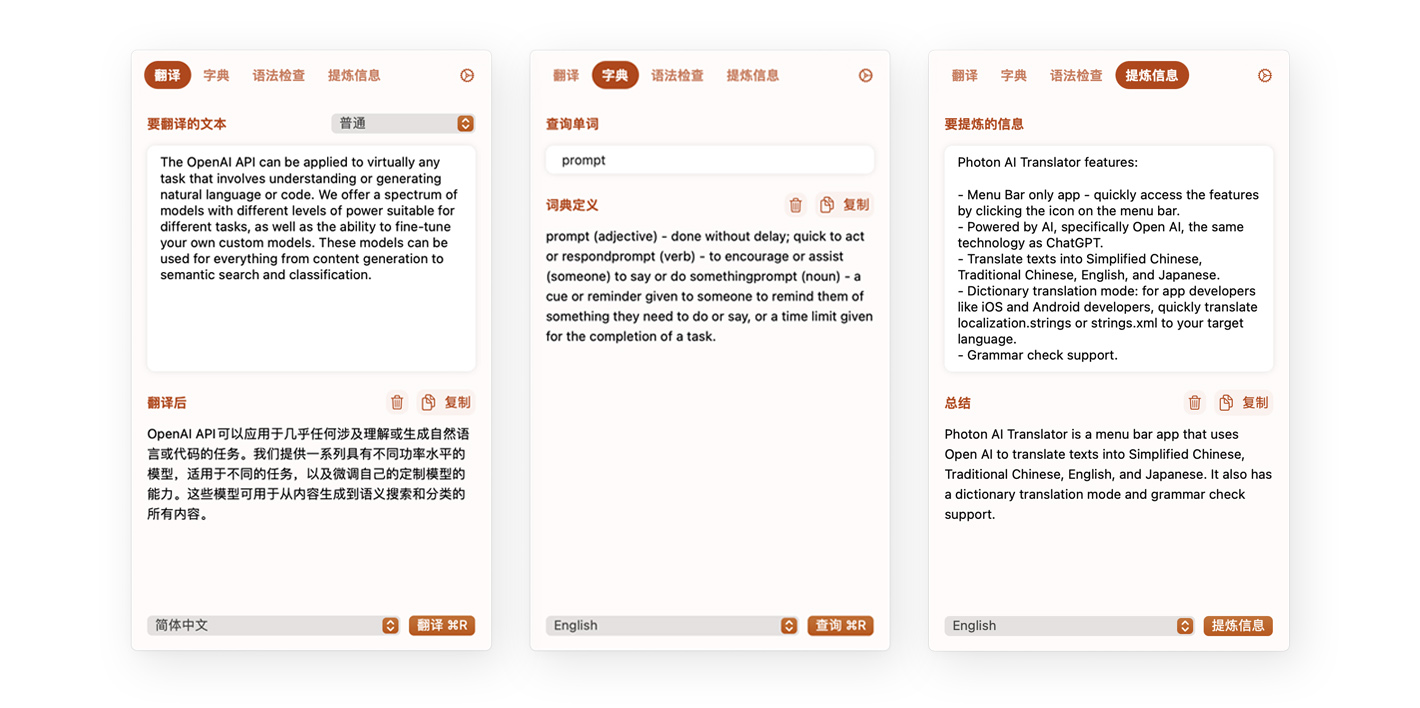
Photon AI Translator 和做产品的一些思考
近 4 个月内我一直在做 Apple 平台的产品,虽然从使用量来说「简体中文」用户是占多数,但我一直有做多语言的支持:英语、简体中文和繁体中文。习惯上 Google 翻译的我,基本上在使用 Xcode 过程中也会一直在浏览器开着 Google Trans…...
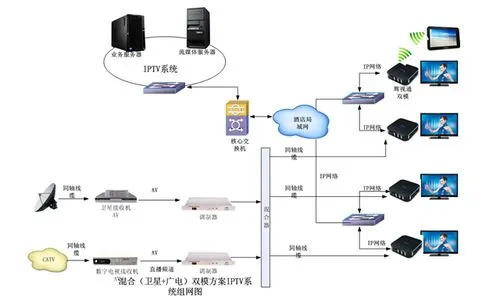
IPTV系统架构的分析与研究
1 引言 IPTV业务是伴随着宽带互联网的飞速发展而兴起的一项新兴的互联网增值业务,它利用宽带互联网的基础设施,以家用电视机和电脑作为主要终端 ,利用网络机顶盒(STB,Set -TopBox) ,通过互联网协议来传送电视信号.提供包括 电视节 目在 内…...
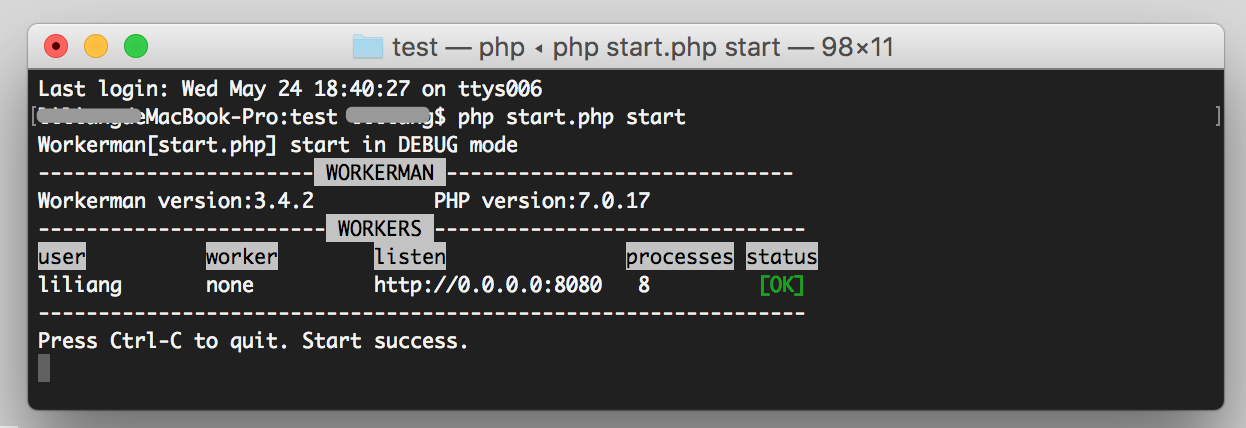
workerman开发者必须知道的几个问题
1、windows环境限制 windows系统下workerman单个进程仅支持200个连接。 windows系统下无法使用count参数设置多进程。 windows系统下无法使用status、stop、reload、restart等命令。 windows系统下无法守护进程,cmd窗口关掉后服务即停止。 windows系统下无法在一个…...
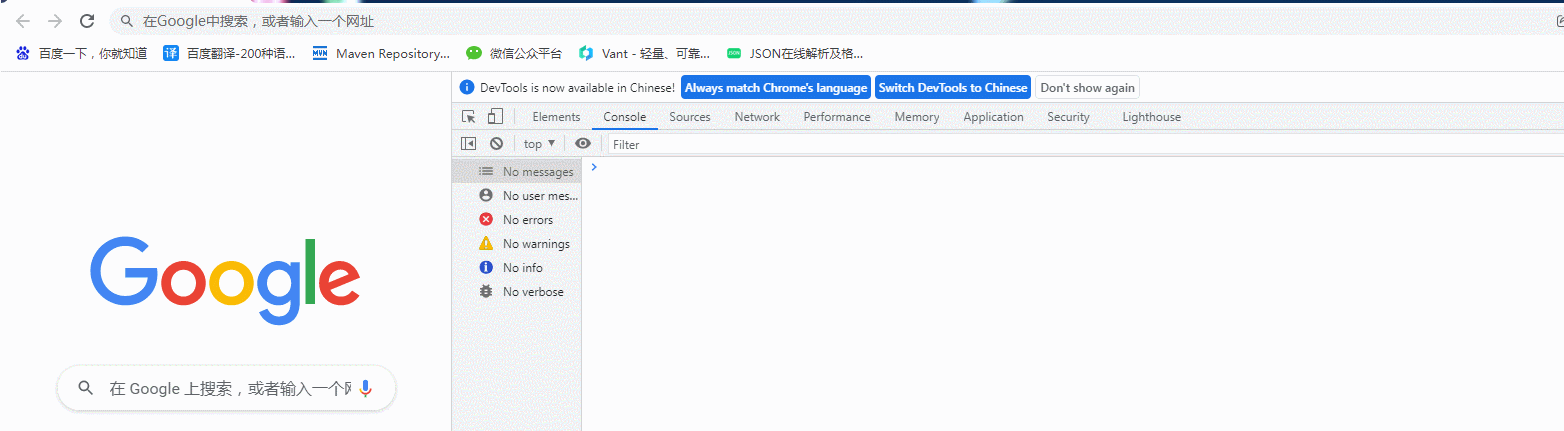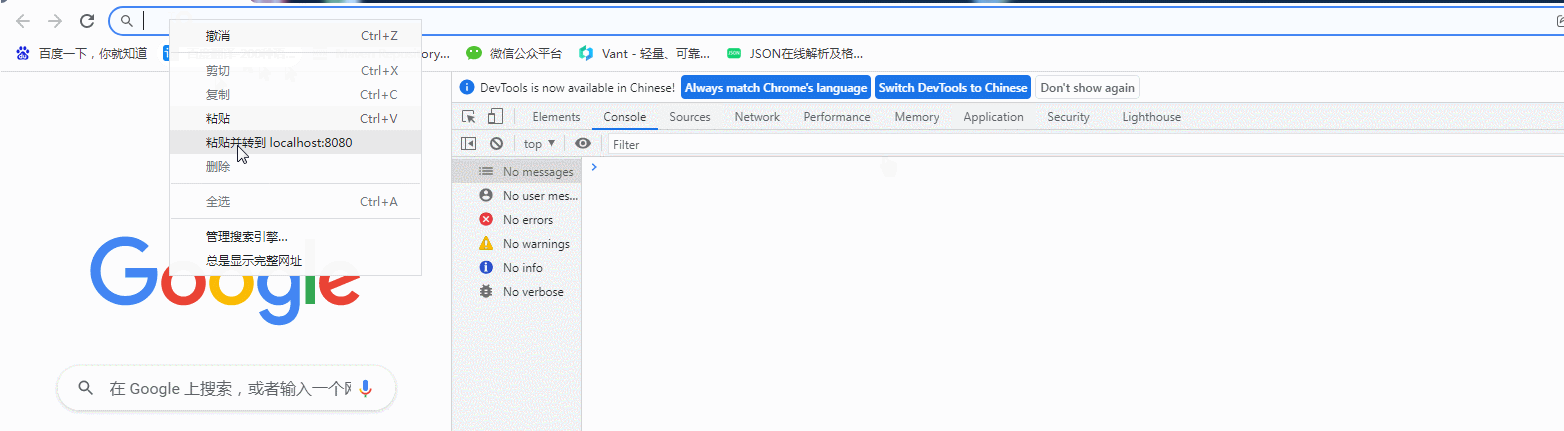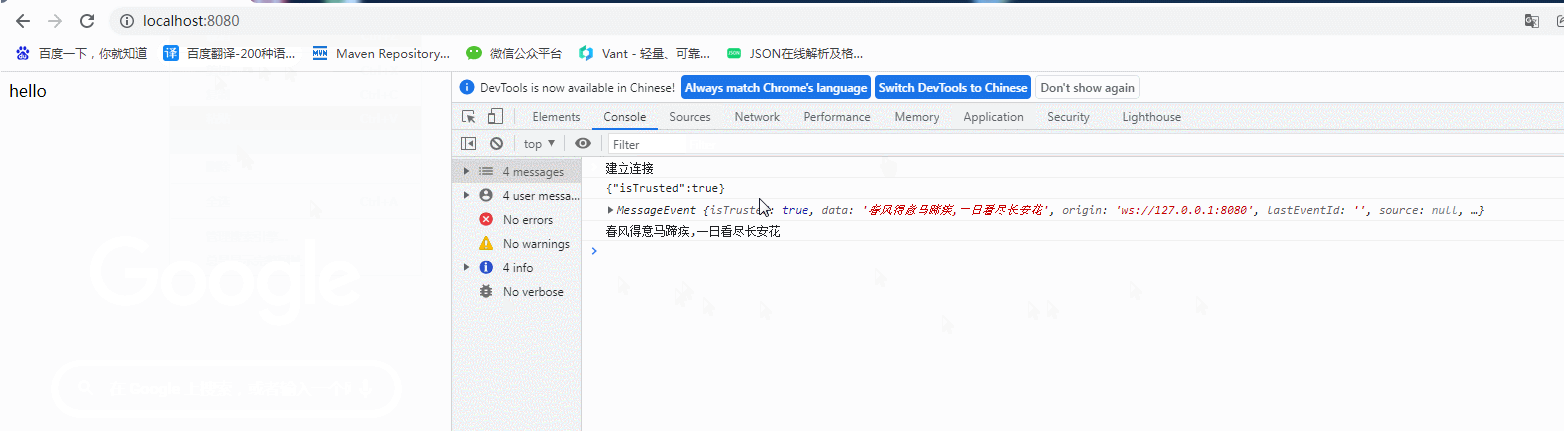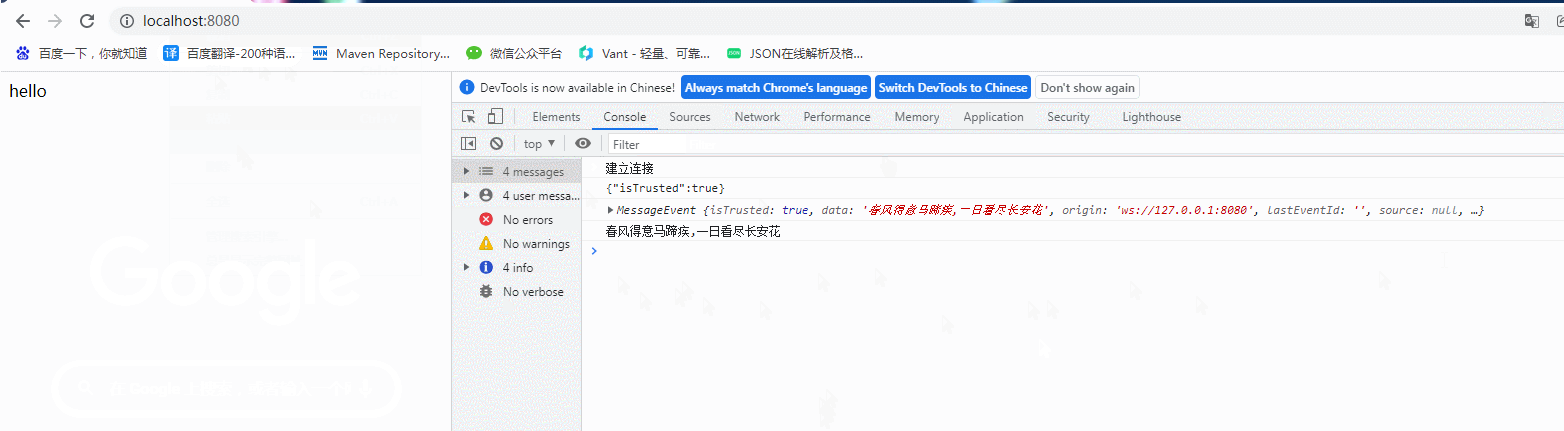
golang Gin实现websocket
golang使用 Gin实现 websocket,这里笔者重新搭建一个项目 1、创建项目安装依赖 项目名为 go-gin-websocket 在指定文件夹下,新建项目文件夹 go-gin-websocket 进入项目文件夹,打开cmd窗口,在项目(go-gin-websocket&a…...
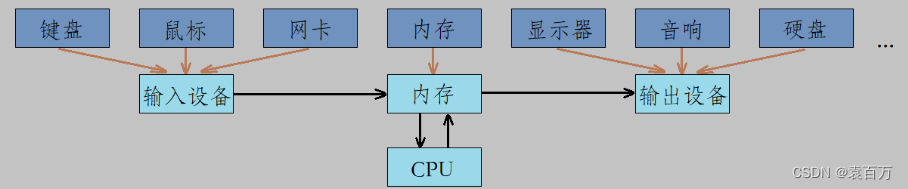
冯·诺依曼体系结构与初始操作系统
目录 冯诺依曼体系结构 冯诺依曼体系结构图 内存 外存 网卡和磁盘 结构之间运算速度的差异 缓冲区 初始操作系统 概念 操作系统上边与下边分别有什么 从上到下依次顺序解析 用户 用户操作接口 系统调用接口 操作系统四项管理 驱动 硬件 冯诺依曼体系结构 冯诺…...
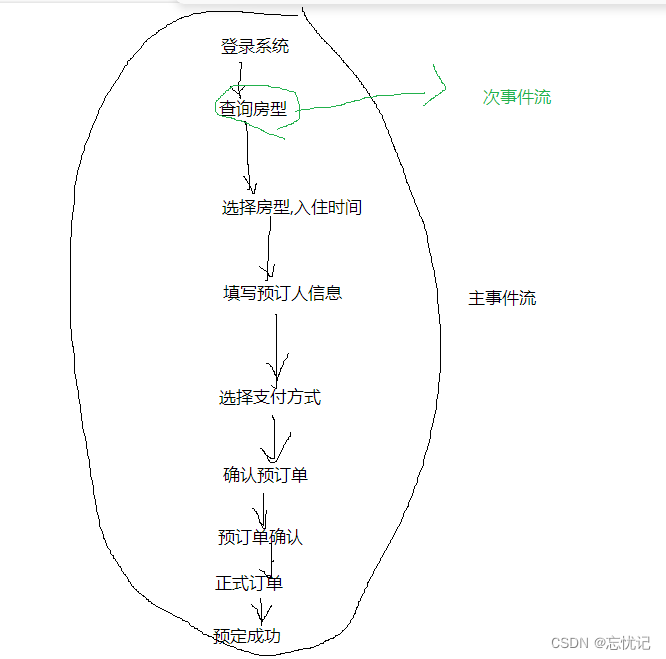
软件测试之黑盒测试的具体方法详解
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一.基于需求的设计方法二.等价类三.边界值四.判定表4.1 **关系**4.2 如何设计测试用例4.3 实际案例第一步第二步第三步第四步 五.正交排列5.1 什么是正交表5.2 …...

图形编辑器:历史记录设计
大家好,我是前端西瓜哥。今天讲一下图形编辑器如何实现历史记录,做到撤销重做。 其实就是版本号的更替。每个版本保存一个状态。 数据结构 要记录图形编辑器的历史记录,支持撤销重做功能,需要两个栈:撤销࿰…...
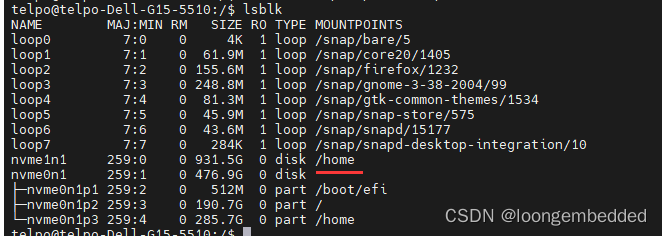
ubuntu22.04下挂载第二块硬盘
文章目录 一、查看硬盘情况二、找到nvme1n1三、挂载四、修改分区文件 一、查看硬盘情况 首先要查看一下系统识别出来的设备。也就是说,我希望知道,ubuntu到底发现了几块硬盘。用命令:lsblk 显示结果如下: 有两块硬盘:…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
