关联爆破-RSA分解
今天遇到一个RSA题,给出n和p+q求分解,翻箱倒柜也没找着原来写的程序,这里重写一下。都是编程的活。
第1种情况,给出p^q
这种情况当p,q相同位相同时为0,不同时为1,爆破的时候只需要逐位判断两种情况,
当为0时p,q都置0或者都置1,
当为1时p,q分别置1
如果给出的p^q是全的可以从低位爆破,爆破的同时跟n的尾数位比较。
这个题我按今天这题的样子把后400位删掉,用的同一个N
N有2048位,所以p,q大概都是1024位,而gift给出是1023位,显然p,q首位为1。然后爆破到400位时用coppersmith方法求剩余部分。
N = 19913283586978731272870374837854045562790864804312115658302463830117436116219931849180682454814957654994095500743161455669517742683196683945049694888375426558735311269294662060482717191409995553476857418604462748567614908456839975140435522714312533340013676955820372105156740228641356206825881138276471973278761948406726062399175269553184359236859175084438349221553915085882218661560890322526503741457647907788204833926214096369428913779871365689037671018942683561649187089844083798834324075157252488088496084629641115161544547506935703532950490109236586524242732310854674446718076810611730874295399180178401471353663
#gift = (P^Q)>>400
gift = 24974037914540444972174719514588697024841724043425510822527893809737860155273716656719332610821905216284030065533729927837282940938990333355929462102999310764824139677295638873649726744154
gift <<=400PR.<x> = PolynomialRing(Zmod(N))
ok = False
def pq_xor(tp,tq,idx):global ok if ok:return if tp*tq>N:return if (tp+(2<<idx))*(tq+(2<<idx))<N:return if idx<=400:try:f = tp + x rr = f.monic().small_roots(X=2^400, beta=0.4)if rr != []:print(rr)print(tp)print('p = ',f(rr[0]))ok = Truereturnexcept:passreturnidx -=1b = (gift >>idx)&1one = 1<<idx if b==0:pq_xor(tp,tq,idx) pq_xor(tp+one,tq+one,idx) else: #1pq_xor(tp+one,tq,idx)pq_xor(tp,tq+one,idx)#N.nbits()=2048 gift.nbits()=1023 p,q的1024位为1
tp = 1<<1023
tq = 1<<1023
pq_xor(tp,tq,1023)
第2种情况,给出p+q
也就是今天遇到的这个题,程序前边基本相同,只在处理下一步分支时有区别。
因为加法有进位,所以两数相加时有8种情况(从高位开始爆破会涉及到有进位的情况)
对应的和有3种情况:0,1,2,3(两数都是1,还有1个进位),然后反过来,
当gift当位剩余b
b==0,p,q都不变进行下一步
b==1,三种情况(p+1,q,gift-1)(p,q+1,gift-1)(p,q,gift)
b==2,三种情况(p+1,q,gift-1)(p,q+1,gift-1)(p+1,q+1,gift-2)
b==3,最后一种(p+1,q+1,gift-2)
这个理起来很绕,好在绕过来了
N = 19913283586978731272870374837854045562790864804312115658302463830117436116219931849180682454814957654994095500743161455669517742683196683945049694888375426558735311269294662060482717191409995553476857418604462748567614908456839975140435522714312533340013676955820372105156740228641356206825881138276471973278761948406726062399175269553184359236859175084438349221553915085882218661560890322526503741457647907788204833926214096369428913779871365689037671018942683561649187089844083798834324075157252488088496084629641115161544547506935703532950490109236586524242732310854674446718076810611730874295399180178401471353663
gift = 112012823249741273956420414320152024086394551241563686416444057368708038459572554871491781707278127933195689073127882065060125127295041489653572915729848455155059117821290550157606860744547
gift = gift<<400PR.<x> = PolynomialRing(Zmod(N))
ok = False
def pq_add(tp,tq,tgift,idx):global ok if ok:return if tp*tq>N:#print('>')return if (tp+(2<<idx))*(tq+(2<<idx))<N:#print('<', hex((tp+(1<<(idx+2))))[:20], hex(tq+(2<<idx))[:20], hex(N)[:20])return if idx<=400:try:f = tp + x rr = f.monic().small_roots(X=2^400, beta=0.4)if rr != []:print(rr)print(tp)print('p = ',f(rr[0]))ok = Truereturnexcept:passreturnidx -=1b = tgift >>idx one = 1<<idx#print(hex(tp)[:20],hex(tq)[:20],hex(tgift)[:20],idx,b)if b==0 or b==1:pq_add(tp,tq,tgift,idx) if b==1 or b==2:pq_add(tp+one,tq,tgift-one,idx)pq_add(tp,tq+one,tgift-one,idx)if b==2 or b==3:pq_add(tp+one,tq+one,tgift-(one<<1),idx)tp = 1<<1023
tq = 1<<1023
tgift = gift -tp -tq
pq_add(tp,tq,tgift,1023)
第三个小题,是p^rev(q)
就是把q反过来再和p异或,这里为了迷惑人用p+q-2*(p&q)来代替p^q
def system_two(m: bytes):p, q = [getPrime(NBITS // 2) for _ in range(2)]n = p * qe = 0x10001ct = pow(bytes_to_long(m), e, n)print(f"n = {n}")print(f"e = {e}")print(f"ct = {ct}")# what if q is reversed?q = int('0b' + ''.join(reversed(bin(q)[2:])), 2)hint = p + q - 2 * (p & q) # hint = p^qprint(f"hint = {hint}")
这个从两端爆破,我分了16种情况,后来整理成一个数组来处理
n = 153342396916538105228389844604657707491428056788672847550697727306332965113688161734184928502340063389805944751606853233980691631740462201365232680640173140929264281005775085463371950848223467977601447652530169573444881112823791610262204408257868244728097216834146410851717107402761308983285697611182983074893
hint = 3551084838077090433831900645555386063043442912976229080632434410289074664593196489335469532063370582988952492150862930160920594215273070573601780382407014bits = 512def get_pq(p,q, idx):t = p*qif t == n:print('!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1')print('p = ', p)print('q = ', q)exit()return Trueif idx>=bits//2:return Falseif t > n:return Falseif ((t^n)&((1<<idx)-1)) != 0:return False#中间全写1,不能小于nk = (1<<(bits - idx) ) - (1<<idx)if (p+k)*(q+k) < n:return False b1 = int(hint[idx])b2 = int(hint[-idx-1])bleft = 1<<(bits-idx-1)bright = 1<<idx'''if (b1 == 1) and (b2 == 1):get_pq(p + bleft + bright, q, idx+1)get_pq(p + bleft, q + bleft, idx+1)get_pq(p + bright, q + bright, idx+1)get_pq(p, q + bleft + bright, idx+1)elif (b1 == 0) and (b2 == 0):get_pq(p + bleft + bright, q + bleft + bright, idx+1)get_pq(p + bleft, q + bright, idx+1)get_pq(p + bright, q + bleft, idx+1)get_pq(p, q, idx+1)elif (b1 == 1) and (b2 == 0):get_pq(p + bleft + bright, q + bleft, idx+1)get_pq(p + bleft, q, idx+1)get_pq(p + bright, q + bleft + bright, idx+1)get_pq(p, q + bright, idx+1)elif (b1 == 0) and (b2 == 1):get_pq(p + bleft + bright, q + bright, idx+1)get_pq(p + bleft, q + bleft + bright, idx+1)get_pq(p + bright, q, idx+1)get_pq(p, q + bleft, idx+1)else:pass''' way = [[[1,1,1,1],[1,0,0,1],[0,1,1,0],[0,0,0,0]], #00左右都相同[[1,1,0,1],[1,0,1,1],[0,1,0,0],[0,0,1,0]], #01左同右不同[[1,1,1,0],[1,0,0,0],[0,1,1,1],[0,0,0,1]], #10右同左不同[[1,1,0,0],[1,0,1,0],[0,1,0,1],[0,0,1,1]], #11左右都不同]for v in way[b1*2+b2]:get_pq(p + v[0]*bleft + v[1]*bright, q + v[2]*bleft + v[3]*bright, idx+1)return Falsehint = bin(hint)[2:].zfill(bits)
print('h:',hint)
p = (1<<(bits-1))+1
q = (1<<(bits-1))+1
get_pq(p,q,1)第四个小题给出p+q,p*q都是10进制无进位
这里运算的时候直接用ascii码运算然后模10(+2,+4)
def add(a,b):if(a<b):a0 = str(b).encode()b0 = str(a).encode()else:a0 = str(a).encode()b0 = str(b).encode()ans = 0for i in range(len(a0)-len(b0)):ans = ans*10+a0[i]-48for i in range(len(b0)):ans = ans*10+(a0[i+len(a0)-len(b0)]+b0[i]+4)%10return ansdef mul(a,b):if(a<b):a0 = str(b).encode()b0 = str(a).encode()else:a0 = str(a).encode()b0 = str(b).encode()ans = 0for i in range(len(b0)):ans = ans*10+((a0[i+len(a0)-len(b0)]+2)*(b0[i]+2))%10return ans
这个虽然是10进制,但处理方式也一样由于给的倍数是全部(尾部完整)所以直接从尾部爆破,与n进行比较,这样每位都都与n的对应位比较,可以裁剪掉大量错误分支,爆破更快。
ppq = '10399034381787849923326924881454040531711492204619924608227265350044149907274051734345037676383421545973249148286183660679683016947030357640361405556516408'[::-1]
ptq = '06004903250672248020273453078045186428048881010508070095760634049430058892705564009054400328070528434060550830050010084328522605000400260581038846465000861'[::-1]
n = 100457237809578238448997689590363740025639066957321554834356116114019566855447194466985968666777662995007348443263561295712530012665535942780881309520544097928921920784417859632308854225762469971326925931642031846400402355926637518199130760304347996335637140724757568332604740023000379088112644537238901495181p,q = [0],[0]
a = [[0 for i in range(10)] for i in range(10)]for i in range(10):for j in range(10):if a[(i+j)%10][(i*j)%10] != 0:a[(i+j)%10][(i*j)%10].extend([i,j])else:a[(i+j)%10][(i*j)%10] = [i,j]l = len(ptq)
mask = 1
for i in range(0, l):tmp, tmq = [],[]for k in range(len(p)):for j in range(0, len(a[int(ppq[i])][int(ptq[i])]), 2):if (a[int(ppq[i])][int(ptq[i])][j] * mask + p[k]) * \(a[int(ppq[i])][int(ptq[i])][j+1] * mask + q[k]) % mask \== n % mask:tmp.append(p[k] + a[int(ppq[i])][int(ptq[i])][j] * mask)tmq.append(q[k] + a[int(ppq[i])][int(ptq[i])][j+1] * mask)p = tmpq = tmq# print(i, len(p), len(q))mask *= 10for i in q+p:if i != 0 and n % i == 0:p = iq = n // ibreak
相关文章:

关联爆破-RSA分解
今天遇到一个RSA题,给出n和pq求分解,翻箱倒柜也没找着原来写的程序,这里重写一下。都是编程的活。 第1种情况,给出p^q 这种情况当p,q相同位相同时为0,不同时为1,爆破的时候只需要逐位判断两种情况&#x…...
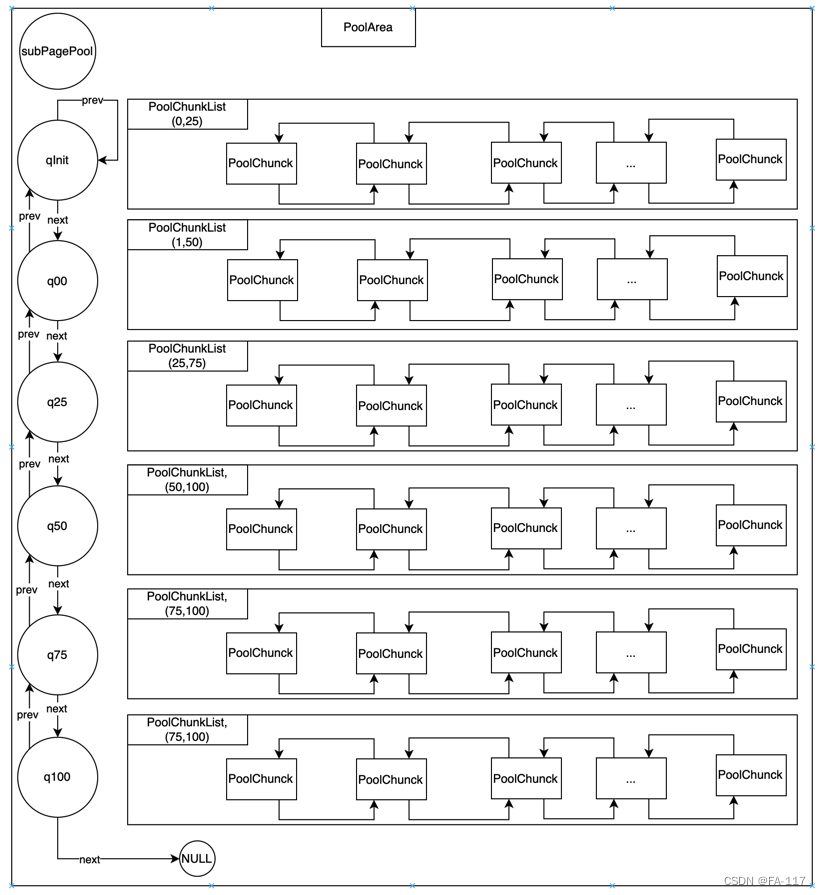
Netty内存管理--内存池PoolArena
一、写在前面 到这里, 想必你已知道了Netty中的内存规格化(SizedClass), Page和SubPage级别的内存分配, 但是具体使用者不应该关心应该申请page还是subpage。而且从过去的经验来说, 申请page/subpage的数量也是个动态值, 如果申请使用完之后就释放那使用内存池的意义就不大。N…...

RabbitMQ 发布订阅模式,routing路由模式,topic模式
发布订阅模式 一个消息可以由多个消费者消费同一个消息 消费者1和2同时消费了该消息 举例 public static void main(String[] args) throws IOException, TimeoutException {//1 创建连接工厂ConnectionFactory connectionFactorynew ConnectionFactory();//2 设置rabbitmq …...
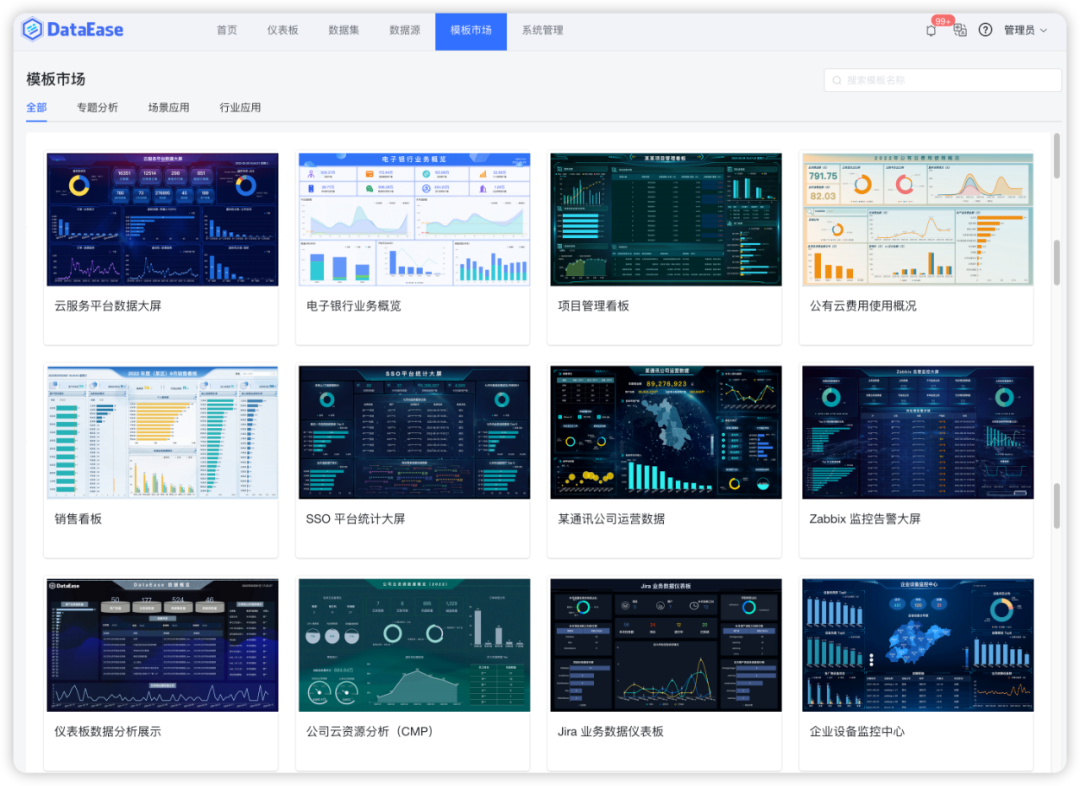
又一款可视化神器,开源了!
在互联网数据大爆炸的这几年,各类数据处理、数据可视化的需求使得 GitHub 上诞生了一大批高质量的 BI 工具。 借助这些 BI 工具,我们能够大幅提升数据分析效率、生成更高质量的项目报告,让用户通过直观的数据看到结果,减低沟通成…...

干货 | 中科院心理所考研复试经验分享
Hello,大家好! 这里是壹脑云科研圈,我是喵君姐姐~ 此时此刻,23年考研的小伙伴估计正在为复试进行准备吧,大家都准备得怎么样了呢? 今天为大家带来的就是我国顶级心理学研究结构—中科院心理所…...
Redis基础知识概述
Redis基础知识概述 文章目录 Redis基础知识概述一、Redis简介二、NoSQL技术三、Redis的高并发和快速原因四、Redis为什么是单线程的 五、单线程的优劣势1、优势2、劣势 六、Redis高并发总结七、在java中使用Redis1、添加Jedis依赖 八、Redis在Java Web中的应用1、存储缓存用的数…...

开心档之C++ 引用
C 引用 引用变量是一个别名,也就是说,它是某个已存在变量的另一个名字。一旦把引用初始化为某个变量,就可以使用该引用名称或变量名称来指向变量。 C 引用 vs 指针 引用很容易与指针混淆,它们之间有三个主要的不同:…...

后台优化主要分为哪些?工作内容及流程是什么?
什么是5G网络优化? 顾名思义就是对4G/5G无线网络进行测试,分析,优化的专业技术工作。网络优化工作的进展程度,直接关系着我们对4G/5G无线网络的使用体验。 网络优化工程师通过对现已运行的手机通话网络进行话务数据分析、现场测…...

二叉树及其遍历
文章目录 二叉树树的定义二叉树的定义遍历先序遍历中序遍历后序遍历层次遍历定义队列层次创建二叉树层次遍历 二叉树 树是一种非线性的数据结构,由若干个节点组成,节点之间存在一种父子关系,具有层次结构。二叉树是一种特殊的树结构ÿ…...
java 版本企业电子招投标采购系统源码之登录页面
信息数智化招采系统 服务框架:Spring Cloud、Spring Boot2、Mybatis、OAuth2、Security 前端架构:VUE、Uniapp、Layui、Bootstrap、H5、CSS3 涉及技术:Eureka、Config、Zuul、OAuth2、Security、OSS、Turbine、Zipkin、Feign、Monitor、…...

第五章 使用RAID与LVM磁盘阵列技术
第五章 使用RAID与LVM磁盘阵列技术 一、RAID磁盘冗余阵列 1、部署磁盘阵列 (1)、RAID0、1、5、10方案技术对比 RAID级别最少硬盘可用容量读写性能安全性特点02nn低追求最大容量和速度,任何一块盘损坏,数据全部异常。12n/2n高追…...

LeetCode 560. 和为 K 的子数组
LeetCode 560. 和为 K 的子数组 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。 示例 1: 输入:nums [1,1,1], k 2 输出:2示例 2: 输入:nums [1,2,3], k 3 …...

后端要一次性返回我10万条数据
问题描述 面试官:后端一次性返回10万条数据给你,你如何处理?我:歪嘴一笑,what the f**k! 问题考察点 看似无厘头的问题,实际上考查候选人知识的广度和深度,虽然在工作中这种情况很少遇到... …...

汽车智能化「出海」红利
在高阶智能座舱中,车载导航产品作为与用户体验息息相关的模块之一,同样也进入了升级迭代周期。 基于高精度地图渲染、高精度定位算法、AR等技术的车道级导航、AR导航等产品快速上车,但同时随着人机交互多模发展以及3D沉浸式用户体验需求趋势下…...
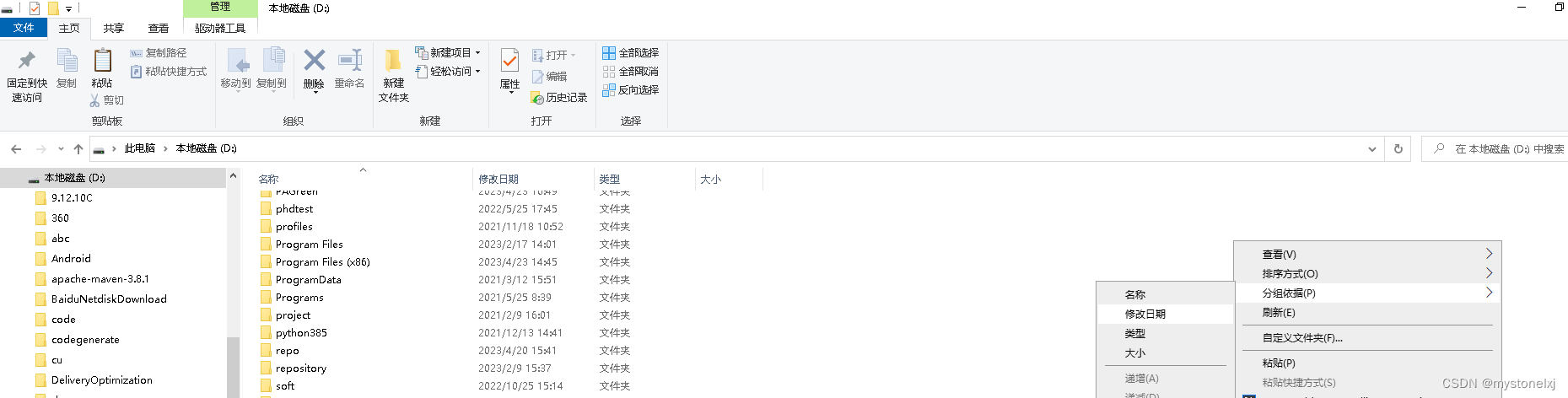
Windows10资源管理器使用
文章目录 前言二、关联菜单操作1.分组展示2.添加选择复选框3.使用窗格模式4.功能区折叠二、“文件夹选项”对话框操作1.访问模式调整2.状态栏控制总结前言 目前Windows系统中的使用较多当属Windows10,资源管理器属于Windows系统中一个常用工具。本文总结了Windows 10 专业版下…...

【视频教程解读】Window上安装和使用autogluon V0.7
1.使用conda安装的python环境 教程使用的是极简版miniconda,由于我们的电脑中安装了anaconda,所以不需要进行进一步安装。python版本为3.9,博客里面有anaconda和python版本的对应关系。注意查看版本autogluon V0.4需要3.8或者3.9和3.10,pip版…...

10、Java继承与多态 - 内部类的概念与分类 1
10、Java继承与多态 - 内部类的概念与分类 1 什么是内部类? 如果一个事物的内部包含另一个事物,那么这就是一个内部包含另一个类,称作内部类; 例如:身体和心脏的关系,又如 -> 汽车和发动机的关系&#x…...

Java SE 面试题
文章目录 Java SE 面试题基本知识请简要介绍 Java SE。请解释 Java 的垃圾回收机制。请解释 Java 中的访问修饰符。 面向对象请解释封装、继承和多态。请解释接口和抽象类的区别。 集合框架请解释 ArrayList 和 LinkedList 的区别。请解释 Set 和 Map 接口。 异常处理请解释 Ja…...
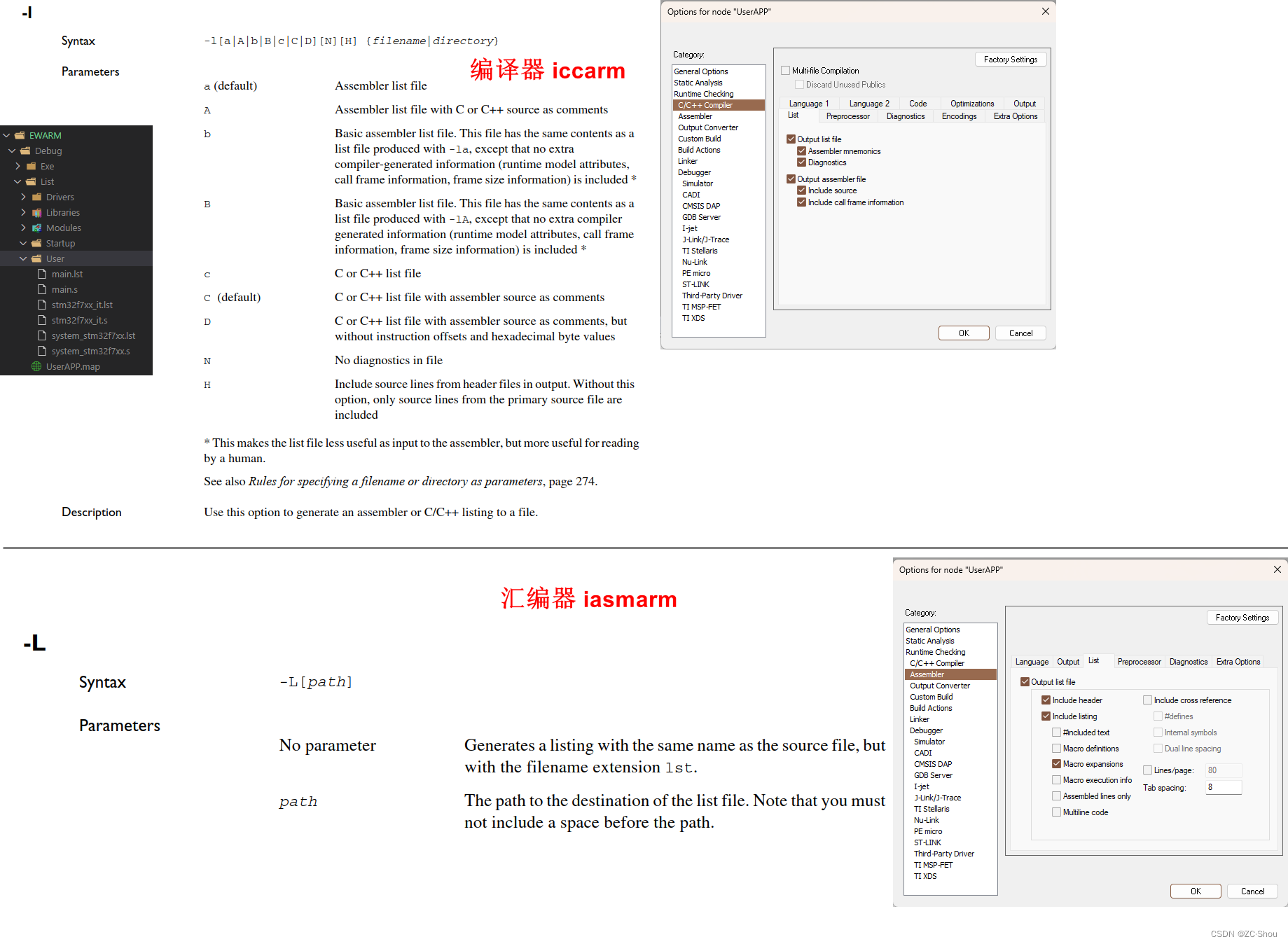
Linux 之十九 编译工具链、.MAP 文件、.LST 文件
.map 文件和 .lst 文件是嵌入式开发中最有用的俩调试辅助文件。现在主要从事 RISC-V 架构,开始与 GCC 打交道,今天就重点学习一下 GCC 的 .map 文件、.lst 文件,并辅助以 ARMCC 和 IAR 作为对比。 编译工具链 .map 文件和 .lst 文件都是由编…...

小 C 的数学(math)
祝大家劳动节快乐!!小手动起来 言归正传┏ (゜ω゜)☞ 题目描述 小 C 想要成为一名 OIer,于是他提前学习数学,为 OI 做好铺垫。这一天,他的数学老师给了一道题:给定正整数 a,以及给定一个区间 …...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
