范数详解-torch.linalg.norm计算实例
文章目录
- 二范数
- F范数
- 核范数
- 无穷范数
- L1范数
- L2范数
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。
范数是一种数学概念,可以将向量或矩阵映射到非负实数上,通常被用来衡量向量或矩阵的大小或距离。在机器学习和数值分析领域中,范数是一种重要的工具,常用于正则化、优化、降维等任务中。
本文以torch.linalg.norm()函数举例,详细讲解F范数、核范数、无穷范数等范数的定义和计算。
参考官方文档https://pytorch.org/docs/stable/generated/torch.linalg.norm.html
由于torch.norm()已弃用,所以以torch.linalg.norm()讲解,也可以使用 NumPy 或者 SciPy 库中的 numpy.linalg.norm 或 scipy.linalg.norm 函数。下图是其支持的各种范数:
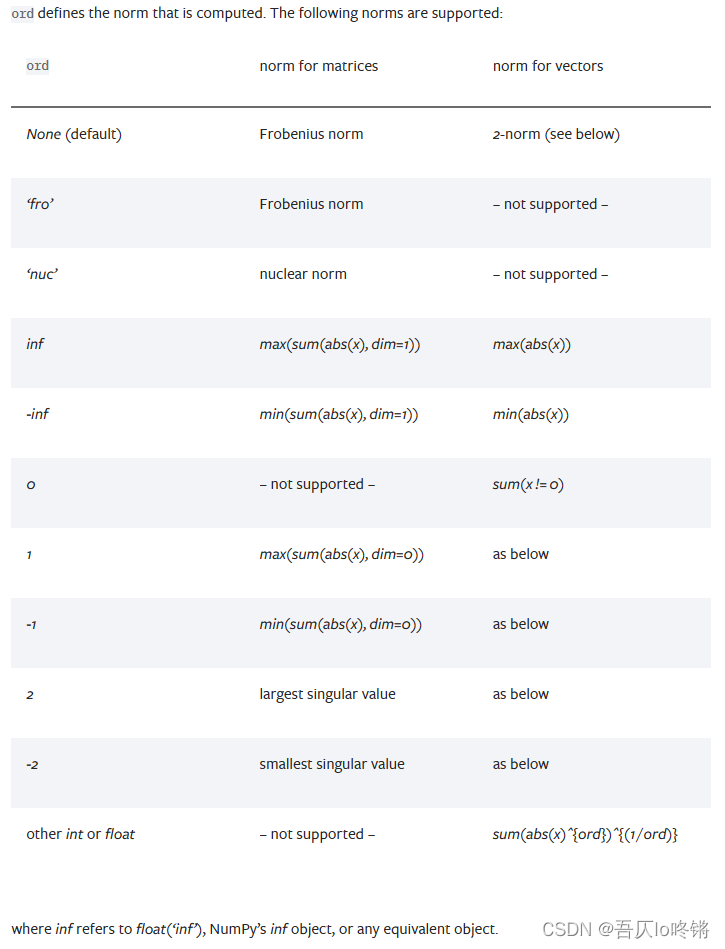
二范数
标准二范数(2-norm)是向量的一种范数,通常用来衡量向量的大小。二范数可以说是出场率最高的了,比如在最小二乘法中,还有如线性代数中的向量空间、矩阵分解等。
标准二范数的一些重要性质包括:
- 非负性:
对于任意向量 x x x,它的标准二范数都是非负的,即 ∣ ∣ x ∣ ∣ 2 ≥ 0 ||x||_2 \geq 0 ∣∣x∣∣2≥0。 - 齐次性:
对于任意向量 x x x和任意实数 k k k,有 ∣ ∣ k x ∣ ∣ 2 = ∣ k ∣ ∣ ∣ x ∣ ∣ 2 ||kx||_2 = |k|||x||_2 ∣∣kx∣∣2=∣k∣∣∣x∣∣2。 - 三角不等式:
对于任意向量 x 和 y,有 ∣ ∣ x + y ∣ ∣ 2 ≤ ∣ ∣ x ∣ ∣ 2 + ∣ ∣ y ∣ ∣ 2 ||x+y||_2\leq ||x||_2+||y||_2 ∣∣x+y∣∣2≤∣∣x∣∣2+∣∣y∣∣2。 - 向量的 Cauchy-Schwarz 不等式:
对于任意向量 x x x和 y y y,有 ∣ x ⋅ y ∣ ≤ ∣ ∣ x ∣ ∣ 2 ∣ ∣ y ∣ ∣ 2 |x·y| \leq ||x||_2 ||y||_2 ∣x⋅y∣≤∣∣x∣∣2∣∣y∣∣2。
对于一个 n n n维向量 x x x,它的标准二范数定义如下:
∣ ∣ x ∣ ∣ 2 = ( ∑ i = 1 n x i 2 ) 1 2 ||x||_2 = (\sum_{i=1}^n x_i^2)^{\frac{1}{2}} ∣∣x∣∣2=(i=1∑nxi2)21
其中, x i x_i xi表示向量 x x x的第 i i i个元素的值。
标准二范数的计算方法类似于欧几里得距离,都是将所有元素的平方和开根号。标准二范数也可以表示为向量的点积和向量的模长的乘积,即:
∣ ∣ x ∣ ∣ 2 = x ⋅ x = ∣ x ∣ x ∣ x ∣ ⋅ x ∣ x ∣ ||x||_2 = \sqrt{x·x}= |x|\sqrt{\frac{x}{|x|}·\frac{x}{|x|}} ∣∣x∣∣2=x⋅x=∣x∣∣x∣x⋅∣x∣x
其中, ⋅ · ⋅表示点积, ∣ x ∣ |x| ∣x∣表示向量 x x x的模长, x ∣ x ∣ \frac{x}{|x|} ∣x∣x表示向量 x x x的单位向量。
在 PyTorch 中,可以使用 torch.linalg.norm 函数来计算向量的标准二范数,例如:
x = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float)norm_2 = torch.linalg.norm(x)print(norm_2)# 输出 7.4162,即 (√(1^2 + 2^2 + 3^2 + 4^2 + 5^2))
F范数
F范数(Frobenius范数)是一种矩阵的范数,用来衡量矩阵的大小。F范数在很多应用中都有重要的作用,例如矩阵近似、矩阵压缩、矩阵分解等。
F范数的一些重要性质包括:
- 非负性
对于任意矩阵 A A A,它的F范数都是非负的,即 ∣ ∣ A ∣ ∣ F ≥ 0 ||A||_F\geq 0 ∣∣A∣∣F≥0。 - 齐次性
对于任意矩阵 A A A和任意实数 k k k,有 ∣ ∣ k A ∣ ∣ F = ∣ k ∣ ∣ ∣ A ∣ ∣ F ||kA||_F = |k|||A||_F ∣∣kA∣∣F=∣k∣∣∣A∣∣F。 - 三角不等式
对于任意矩阵 A A A和 B B B,有 ∣ ∣ A + B ∣ ∣ F ≤ ∣ ∣ A ∣ ∣ F + ∣ ∣ B ∣ ∣ F ||A+B||_F\leq ||A||_F + ||B||_F ∣∣A+B∣∣F≤∣∣A∣∣F+∣∣B∣∣F。 - 特殊性质
对于一个正交矩阵 Q Q Q,它的F范数等于 1,即 ∣ ∣ Q ∣ ∣ F = 1 ||Q||_F=1 ∣∣Q∣∣F=1。
对于一个 n n n行 m m m列的矩阵 A A A,它的F范数定义如下:
∣ ∣ A ∣ ∣ F = ( ∑ i = 1 n ∑ j = 1 m A i j 2 ) 1 2 ||A||_F = (\sum_{i=1}^n\sum_{j=1}^mA_{ij}^2)^{\frac{1}{2}} ∣∣A∣∣F=(i=1∑nj=1∑mAij2)21
其中, A i j A_{ij} Aij表示矩阵 A A A的第 i i i行第 j j j列元素的值。
F范数的计算方法类似于标准二范数,都是将所有元素的平方和开根号。与标准二范数不同的是,F范数的加和是在矩阵的所有元素上进行的,而不是在向量的所有元素上进行的。
在 PyTorch 中,可以使用 torch.linalg.norm 函数来计算矩阵的F范数,其对应的参数为 ord='fro',例如:
A = torch.tensor([[1, 2],[3, 4],[5, 6]], dtype=torch.float)norm_F = torch.linalg.norm(A, ord='fro')print(norm_F) # 输出 9.5394,即 (√(1^2 + 2^2 + 3^2 + 4^2 + 5^2 + 6^2))
核范数
核范数(nuclear norm),也称为矩阵1-范数(matrix 1-norm),也是一种用于衡量矩阵的大小的范数。核范数在矩阵分解、矩阵压缩、矩阵近似等方面有广泛的应用。例如在矩阵分解中,核范数可以用于衡量原始矩阵与分解后的矩阵的差异程度,从而可以优化分解的结果。
核范数的一些重要性质包括:
- 非负性:
对于任意矩阵 A A A,它的核范数都是非负的,即 ∣ ∣ A ∣ ∣ ∗ ≥ 0 ||A||_* \geq 0 ∣∣A∣∣∗≥0。 - 齐次性:
对于任意矩阵 A A A和任意实数 k k k,有 ∣ ∣ k A ∣ ∣ ∗ = ∣ k ∣ ∣ ∣ A ∣ ∣ ∗ ||kA||_* = |k| ||A||_* ∣∣kA∣∣∗=∣k∣∣∣A∣∣∗。 - 子加性:
对于任意矩阵 A A A和 B B B,有 ∣ ∣ A + B ∣ ∣ ∗ ≤ ∣ ∣ A ∣ ∣ ∗ + ∣ ∣ B ∣ ∣ ∗ ||A+B||_* \leq ||A||_* + ||B||_* ∣∣A+B∣∣∗≤∣∣A∣∣∗+∣∣B∣∣∗。 - 矩阵的谱范数性质:
对于任意矩阵 A A A,有 ∣ ∣ A ∣ ∣ ∗ = ∣ ∣ A T ∣ ∣ ∗ = ∣ ∣ A H ∣ ∣ ∗ ||A||_* = ||A^T||_* = ||A^H||_* ∣∣A∣∣∗=∣∣AT∣∣∗=∣∣AH∣∣∗,其中 A H A^H AH是矩阵 A A A的共轭转置。
对于一个矩阵 A A A,它的核范数定义如下:
∣ ∣ A ∣ ∣ ∗ = ∑ i σ i ||A||_* = \sum_i\sigma_i ∣∣A∣∣∗=i∑σi
其中, σ i \sigma_i σi是矩阵 A A A的奇异值(singular value),表示矩阵 A A A的第 i i i大的奇异值。核范数的计算方法是将矩阵 A 奇异值的绝对值相加。
奇异值分解(singular value decomposition,SVD)是一种常用的矩阵分解方法,用于将一个矩阵分解为三个矩阵的乘积,即
A = U Σ V T A = UΣVᵀ A=UΣVT
具体求解这里不过多展开,可以理解为一种压缩分解技术,原本很大的矩阵,现在只需3个小矩阵就能存储,可以使用torch.svd()进行奇异值分解。
在 PyTorch 中,可以使用 torch.linalg.norm 函数来计算矩阵的核范数,其对应的参数为 ord='nuc',例如:
A = torch.tensor([[1, 2, 3],[4, 5, 6],[7, 8, 9]], dtype=torch.float)norm_nuclear = torch.linalg.norm(A, ord='nuc')u, s, v = torch.svd(A)print(s)print(norm_nuclear)# 输出 17.9165,即 1.6848e+01 + 1.0684e+00 + 2.3721e-07

注:不同函数封装的奇异值分解算法可能不同,得到奇异值可能有些许出入,但应都在一个数量级。
(
插播反爬信息)博主CSDN地址:https://wzlodq.blog.csdn.net/
无穷范数
无穷范数是矩阵的一种范数,也称为最大值范数或者列范数。无穷范数在矩阵计算和优化中有广泛的应用。例如,在矩阵乘法中,可以使用无穷范数来衡量矩阵乘积的大小;在优化问题中,可以使用无穷范数作为约束条件或者目标函数。
无穷范数也有一些重要的性质,包括:
- 非负性
对于任意矩阵 A A A,它的无穷范数都是非负的,即 ∣ ∣ A ∣ ∣ ∞ ≥ 0 ||A||_\infty \geq 0 ∣∣A∣∣∞≥0。 - 齐次性
对于任意矩阵 A A A和任意实数 k k k,有 ∣ ∣ k A ∣ ∣ ∞ = ∣ k ∣ ∣ ∣ A ∣ ∣ ∞ ||kA||_\infty = |k| ||A||_\infty ∣∣kA∣∣∞=∣k∣∣∣A∣∣∞。 - 三角不等式
对于任意矩阵 A A A和 B B B,有 ∣ ∣ A + B ∣ ∣ ∞ ≤ ∣ ∣ A ∣ ∣ ∞ + ∣ ∣ B ∣ ∣ ∞ ||A+B||_\infty \leq ||A||_\infty + ||B||_\infty ∣∣A+B∣∣∞≤∣∣A∣∣∞+∣∣B∣∣∞。 - 矩阵乘法性质
对于任意矩阵 A A A和 B B B,有 ∣ ∣ A B ∣ ∣ ∞ ≤ ∣ ∣ A ∣ ∣ ∞ ∣ ∣ B ∣ ∣ ∞ ||AB||_\infty \leq ||A||_\infty ||B||_\infty ∣∣AB∣∣∞≤∣∣A∣∣∞∣∣B∣∣∞。
对于一个 m × n m\times n m×n的矩阵 A A A,它的无穷范数定义为:
∣ ∣ A ∣ ∣ ∞ = max 1 ≤ i ≤ m ∑ j = 1 n ∣ a i j ∣ ||A||{\infty} = \max_{1\leq i\leq m} \sum_{j=1}^{n} |a_{ij}| ∣∣A∣∣∞=1≤i≤mmaxj=1∑n∣aij∣
其中, i i i的取值范围是 [ 1 , m ] [1, m] [1,m],表示矩阵 A A A的第 i i i行; j j j的取值范围是 [ 1 , n ] [1, n] [1,n],表示矩阵 A A A的第 j j j列。换句话说,无穷范数是将每一列的绝对值相加,然后取其中的最大值。
PyTorch 中其对应的参数为ord='inf',例如:
A = torch.tensor([[1, 2, 3],[4, 5, 6],[7, 8, 9]], dtype=torch.float)norm_inf = np.linalg.norm(A, ord=np.inf)print(norm_inf)# 输出 24,即 max{1+2+3, 4+5+6, 7+8+9}
同理,ord='-inf'表示取最小值。
需要注意的是,计算矩阵的无穷范数比计算其他范数更加简单和快速,因为只需要对每一列的绝对值相加,然后取其中的最大值即可。
L1范数
L1 范数(L1 norm)是指向量中各个元素的绝对值之和,也称为曼哈顿距离(Manhattan distance)或城市街区距离(city block distance)。
L1 范数可以被用于衡量向量或矩阵中各个元素的绝对大小,具有一些特殊的性质,例如对于稀疏向量,它的 L1 范数更容易被最小化,因为它倾向于将向量的一些元素设为 0。
与无穷范数类似,L1 范数也具有一些重要的性质,包括非负性、齐次性、三角不等式和矩阵乘法性质。在矩阵计算和优化中,L1 范数也有广泛的应用。例如,在稀疏信号处理中,可以使用 L1 范数来促进信号的稀疏性;在机器学习中,可以使用 L1 范数作为正则化项来防止过拟合。
对于一个 m × n m \times n m×n的矩阵 A A A,它的 L1 范数定义为:
∣ A ∣ 1 = max 1 ≤ j ≤ n ∑ i = 1 m ∣ a i j ∣ |A|_1 = \max_{1\leq j\leq n} \sum_{i=1}^{m} |a_{ij}| ∣A∣1=1≤j≤nmaxi=1∑m∣aij∣
其中, j j j表示矩阵 A A A的第 j j j列, ∑ i = 1 m ∣ a i j ∣ \sum_{i=1}^{m} |a_{ij}| ∑i=1m∣aij∣表示第 j j j 列中各个元素的绝对值之和。换句话说,L1 范数是将每一列的绝对值相加,然后取其中的最大值。
PyTorch 中其对应的参数为ord='1',例如:
A = torch.tensor([[1, 2, 3],[4, 5, 6],[7, 8, 9]],dtype=torch.float)norm_1 = np.linalg.norm(A, ord=1)print(norm_1)# 输出 18,即 max{1+4+7, 2+5+8, 3+6+9}
同理ord=-1表示取最小值。
L2范数
L2范数(L2 norm)也称为谱范数(spectral norm),或者最大奇异值范数(maximum singular value norm),是矩阵范数中的一种。
L2范数可以被用于衡量向量的大小,也可以被用于衡量向量之间的距离,具有一些特殊的性质,例如在最小化误差的时候,L2范数可以找到唯一的最小化点,而L1范数可能有多个最小化点。
对于一个 m × n m \times n m×n 的矩阵 A A A,它的L2范数定义为:
∣ A ∣ 2 = σ max ( A ) |A|_2 = \sigma_{\max}(A) ∣A∣2=σmax(A)
其中, ∣ ⋅ ∣ 2 |\cdot|_2 ∣⋅∣2 表示向量的 L2 范数, σ max ( A ) \sigma{\max}(A) σmax(A) 表示矩阵 A A A 的最大奇异值(singular value)。
在实际应用中,计算矩阵的 L2 范数可以使用 SVD 分解,例如:
PyTorch 中其对应的参数为ord='2',例如:
A = torch.tensor([[1, 2, 3],[4, 5, 6], [7, 8, 9]], dtype=torch.float)norm_2 = torch.linalg.norm(A, ord=2)u, s, v = torch.svd(A)print(s)print(norm_2)# 输出 16.84810352325432
同理ord=-2表示取最小奇异值。
原创不易,请勿转载(
本不富裕的访问量雪上加霜)
博主首页:https://wzlodq.blog.csdn.net/
来都来了,不评论两句吗👀
如果文章对你有帮助,记得一键三连❤
相关文章:

范数详解-torch.linalg.norm计算实例
文章目录 二范数F范数核范数无穷范数L1范数L2范数 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 范数是一种数学概念,可以将向量或矩阵映射到非负实数上,通常被…...

postgresdb备份脚本
以下是一个简单的postgresdb备份脚本示例: 复制 #!/bin/bash # 设置备份目录和文件名 BACKUP_DIR/path/to/backup BACKUP_FILEdb_backup_$(date %F_%H-%M-%S).sql # 设置数据库连接参数 DB_HOSTlocalhost DB_PORT5432 DB_NAMEmydatabase DB_USERmyusername DB_PA…...

MATLAB程序员投简历的技巧解析,如何写出有亮点的简历
如果你想在简历中展示你的项目经验,一定要有亮点。一个导出的 Excel 文件过大导致浏览器卡顿的例子就是一个很好的亮点。你可以在简历中写明这个例子。如果面试官问起,可以用浏览器的原理来解释。浏览器内核可以简单地分为以下 5 个线程:GUI …...

颜色空间转换RGB-YCbCr
颜色空间 颜色空间(Color Space)是描述颜色的一种方式,它是一个由数学模型表示的三维空间,通常用于将数字表示的颜色转换成可见的颜色。颜色空间的不同取决于所选的坐标轴和原点,以及用于表示颜色的色彩模型。在计算机…...

年薪40万程序员辞职炒股,把一年工资亏光了,得了抑郁症,太惨了
年薪40万的程序员辞职全职炒股 把一年的工资亏光了 得了抑郁症 刚才在网上看了一篇文章 是一位北京的一位在互联网 大厂上班的程序员 在去年就是股市行情比较好的时候 他买了30多万股票 结果连续三个月都赚钱 然后呢 他是就把每天就996这种工作就辞掉了 然后在家全是炒股 感觉炒…...
10分钟如何轻松掌握JMeter使用方法?
目录 引言 安装jmeter HTTP信息头管理器 JMeter断言 HTTP请求默认值来代替所有的域名与端口 JSON提取器来替换变量 结语 引言 想要了解网站或应用程序的性能极限,JMeter是一个不可或缺的工具。但是,对于初学者来说,该如何上手使用JMe…...
[NLP]如何训练自己的大型语言模型
简介 大型语言模型,如OpenAI的GPT-4或Google的PaLM,已经席卷了人工智能领域。然而,大多数公司目前没有能力训练这些模型,并且完全依赖于只有少数几家大型科技公司提供技术支持。 在Replit,我们投入了大量资源来建立从…...
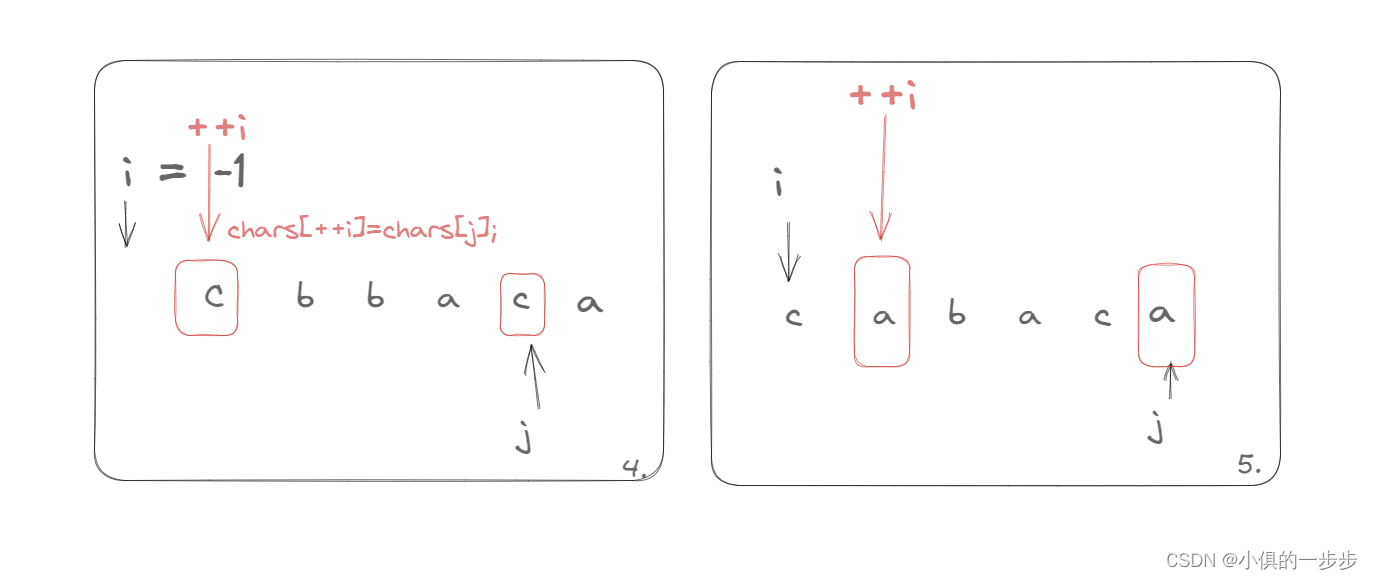
LeetCode1047. 删除字符串中的所有相邻重复项
1047. 删除字符串中的所有相邻重复项 给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。 在 S 上反复执行重复项删除操作,直到无法继续删除。 在完成所有重复项删除操作后返回最终的字符串。答案保证唯一…...
)
3。数据结构(3)
嵌入式软件开发第三部分,各类常用的数据结构及扩展,良好的数据结构选择是保证程序稳定运行的关键,(1)部分包括数组,链表,栈,队列。(2)部分包括树,…...

QT停靠窗口QDockWidget类
QT停靠窗口QDockWidget类 QDockWidget类简介函数和方法讲解 QDockWidget类简介 QDockWidget 类提供了一个部件,它可以停靠在 QMainWindow 内或作为桌面上的顶级窗口浮动。 QDockWidget 提供了停靠窗口部件的概念,也称为工具面板或实用程序窗口。 停靠窗…...

【LeetCode】139. 单词拆分
139. 单词拆分(中等) 思路 首先将大问题分解成小问题: 前 i 个字符的子串,能否分解成单词;剩余子串,是否为单个单词; 动态规划的四个步骤: 确定 dp 数组以及下标的含义 dp[i] 表示 s…...

【三维重建】NeRF原理+代码讲解
文章目录 一、技术原理1.概览2.基于神经辐射场(Neural Radiance Field)的体素渲染算法3.体素渲染算法4.位置信息编码(Positional encoding)5.多层级体素采样 二、代码讲解1.数据读入2.创建nerf1.计算焦距focal与其他设置2.get_emb…...
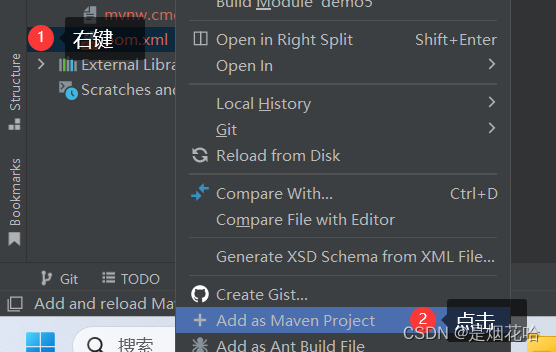
IntelliJ IDEA 社区版2021.3配置SpringBoot项目详细教程及错误解决方法
目录 一、SpringBoot的定义 二、Spring Boot 优点 三、创建一个springboot的项目 四、使用IDEA创建SpringBoot失败案例 一、SpringBoot的定义 Spring 的诞⽣是为了简化 Java 程序的开发的,⽽ Spring Boot 的诞⽣是为了简化 Spring 程序开发的。 Spring Boot 翻…...
Qt中QDebug的使用
QDebug类为调试信息(debugging information)提供输出流。它的声明在<QDebug>中,实现在Core模块中。将调试或跟踪信息(debugging or tracing information)写出到device, file, string or console时都会使用QDebug。 此类的成员函数参考:https://doc…...

vue使用路由的query配置项时如何清除地址栏的参数
写vue项目时,如果想通过路由的query配置项把参数从一个组件传到另一个组件,但是又不希望?idxxx显示在地址栏(如:http://localhost:8080/test?idxxx的?idxxx),该怎么做: 举一个案例࿱…...
)
Redis-列表(List)
Redis列表(List) 介绍 单键多值Redis 列表是简单的字符串列表,按照插入顺序排序。你可以添加一个元素到列表的头部(左边)或者尾部(右边)它的底层实际是个双向链表,对两端的操作性能很高,通过索…...

ripro主题修改教程-首页搜索框美化教程
先看效果图: 我们来看怎么实现: 1、找到wp-content/themes/ripro/assets/css/diy.css并将下面的内容整体复制进去并保存 /*首页搜索框*/ .bgcolor-fff {background-color: #fff; } .row,.navbar .menu-item-mega>.sub-menu{margin-left:-10px;margin-right:-10px;} .home…...

写作业用白光还是暖光?盘点色温4000K的护眼台灯
台灯的白光或者暖光指的是台灯的色温,低色温的光线看起来发黄发红,高色温的光线发白发蓝。 如果灯光的光源是高品质光源,本身没有蓝光问题,那么色温的选择对护眼的影响是比较少的,更多的是对人学习工作状态,…...
-- SimpleDateFormat类)
Java时间类(一)-- SimpleDateFormat类
目录 1. SimpleDateFormat的构造方法: 时间模式字母: 2. SimpleDateFormat的常用方法: “工欲善其事,必先利其器”。学习时间类之前,需要先学习SimpleDateFormat类。 java.text.SimpleDateFormat类是以与语言环境有关的方式来格式...
07 Kubernetes 网络与服务管理
课件 Kubernetes Service是一个抽象层,用于定义一组Pod的访问方式和访问策略,其作用是将一组Pod封装成一个服务,提供一个稳定的虚拟IP地址和端口号,以便于其他应用程序或服务进行访问。 以下是Kubernetes Service YAML配置文件的…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
