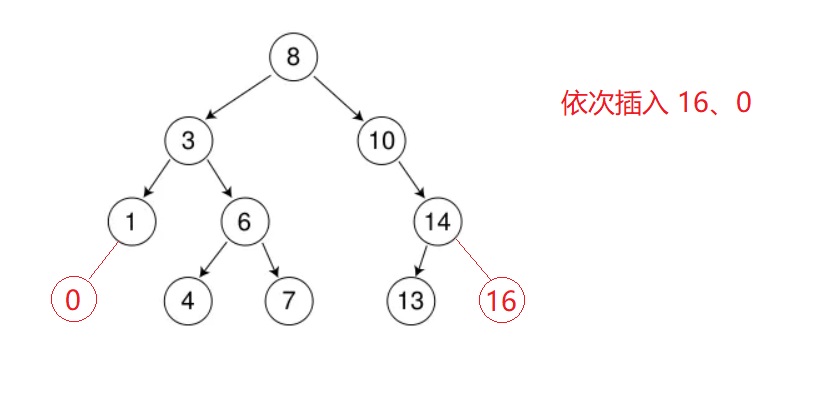
二叉搜索树
1.二叉搜索树
1.1.二叉搜索树概念
二叉搜索树又称二叉排序树,它或者是一颗空树,或者是具有一下性质的二叉树。
- 若它的左子树不为空,则左子树上的所有节点的值都小于根节点的值。
- 若它的右子树不为空,则右子树上的所有节点的值都大于根节点的值。
- 它的左右子树也分别为二叉搜索树。
1.2.二叉搜索树操作
- 二叉搜索树的查找
a. 从根开始比较,查找,比根大则往右边查找,比跟小则往左边走查找。b. 最多查找高度次,走到空,还没找到,这个值不存在。
- 二叉搜索树的插入
树为空,则直接增加节点,赋值给root指针,树不为空,按二叉搜索树性质查找插入位置,插入新节点。
- 二叉搜索树的删除
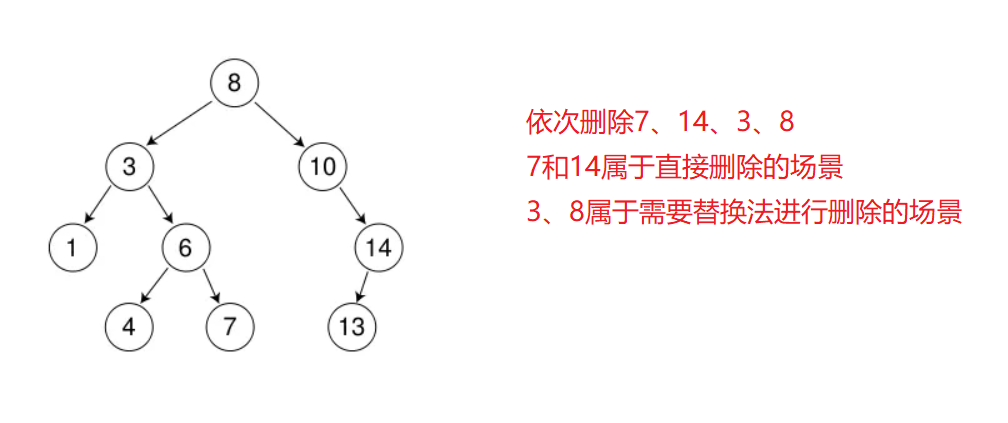
首先查找元素是否在二叉搜索树中,如果不存在,则返回,否则要删除的节点可能分下面四种情况。
- 要删除的节点无孩子节点
- 要删除的节点只有左孩子节点
- 要删除的节点只有右孩子节点
- 要删除的节点有左右孩子节点
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正删除过程如下:
- 情况b:删除该节点且使被删除节点的双亲节点指向被删除节点的左孩子节点-直接删除。
- 情况c:删除该节点且使被删除节点的双亲节点指向被删除节点的右孩子节点-直接删除。
- 情况d:在它的右子树中寻找中序下第一个节点(关键码最小),用它的值填补到被删除节点中,再来处理该节点的删除问题–替换法删除。
1.3.二叉搜索树的模拟实现
template <class K>
struct BSTreeNode
{struct BSTreeNode* left;struct BSTreeNode* right;K key;BSTreeNode(const K& key):key(key),left(nullptr),right(nullptr){}
};template <class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:BSTree():_root(nullptr){}BSTree(const BSTree<K>& t){_root = Copyt(t._root);}BSTree<K>& operator=(BSTree t){swap(_root, t._root);return *this;}~BSTree(){Destory(_root);}bool Insert(const K& key){if (_root == nullptr) {_root = new Node(key);return true;}Node* parent = _root;Node* cur = _root;while (cur != nullptr){if (cur->key < key){parent = cur;cur = cur->right;}else if (cur->key > key){parent = cur;cur = cur->left;}elsereturn false;}if (parent->key < key){parent->right = new Node(key);}else{parent->left = new Node(key);}return true;}void InOrder(){_InOrder(_root);cout << endl;}bool Find(const K& key){if (_root == nullptr)return false;Node* cur = _root;while (cur != nullptr){if (cur->key < key){cur = cur->right;}else if (cur->key < key){cur = cur->left;}elsereturn true;}return false;}bool Erase(const K& key){Node* parent = _root;Node* cur = _root;while (cur != nullptr){if (cur->key > key){parent = cur;cur = cur->left;}else if (cur->key < key){parent = cur;cur = cur->right;}else{Node* del = cur;//到这里,成功的找到这个元素,删除的情况分三种//1.左为空if (cur->left == nullptr){if (cur == _root){_root = cur->right;}else{if (parent->right == cur){parent->right = cur->right;}else{parent->left = cur->right;}}}//2.右为空else if (cur->right == nullptr){if (cur == _root){_root = cur->left;}else{if (parent->right = cur){parent->right = cur->left;}else{parent->left = cur->left;}}}//3.左右都不为空,用的是替换法,左边最大,右边最小(这里用右最小)else{Node* minRight = cur->right;//minRight就是右最大while (minRight->left != nullptr){parent = minRight;minRight = minRight->left;}swap(cur->key, minRight->key);if (parent->left == minRight){parent->left = minRight->right;}else{parent->right = minRight->right;}cur = minRight;}delete cur;return true;}}return false;}bool FindR(const K& key){return _FindR(_root,key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}
private://释放走一个后续遍历void Destory(Node* root){if (root == nullptr)return;Destory(root->left);Destory(root->right);delete root;}Node* Copyt(const Node* root){if (root == nullptr){return nullptr;}Node* parent = new Node(root->key);parent->left = Copyt(root->left);parent->right = Copyt(root->right);return parent;}void _InOrder(Node* _root){if (_root == nullptr)return;_InOrder(_root->left);cout << _root->key << " ";_InOrder(_root->right);}bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->key < key){return _EraseR(root->right, key);}else if (root->key > key){return _EraseR(root->left, key);}else{//三种情况//1.左为空Node* del = root;if (root->left == nullptr){root = root->right;}//2.右为空else if (root->right == nullptr){root = root->left;}//3.左右都不为空else{Node* minRight = root->right;while (minRight->left != nullptr){minRight = minRight->left;}swap(root->key, minRight->key);return _EraseR(root->right, key);}delete del;return true;}}bool _FindR(Node* root,const K& key){if (root == nullptr){return false;}if (root->key < key){_FindR(root->right, key);}else if (root->key > key){_FindR(root->left, key);}else{return true;}}bool _InsertR(Node* &root,const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->key < key){_InsertR(root->right, key);}else if (root->key > key){_InsertR(root->left, key);}else{return false;}return false;}//bool _InsertR(Node* root, const K& key)//{// if (_root == nullptr)// {// _root = new Node(key);// return true;// }// if (root->key < key) {// if (root->right == nullptr)// {// root->right = new Node(key);// return true;// }// _InsertR(root->right, key);// }// else if (root->key > key) {// if (root->left == nullptr)// {// root->left = new Node(key);// return true;// }// _InsertR(root->left, key);// }// else// return false;// return true;//}protected:Node* _root = nullptr;
};
2.二叉搜索树的应用
- K模型:K模型即只有key作为关键码,结构体只需要存储key即可,关键码即为需要搜索到的值。
比如:给一个单词Word,判断该单词是否拼写正确。
在二叉搜索树中检查该单词是否存在,存在则拼写正确,不存在则拼写错误。
- KV模型:每一个关键码key,都有与之对应的值Value,即<Key,Value>的键值对,这种方式在现实生活中非常常见。
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<Word,Chinese>就构成一种键值对;
- 再比如统计单调次数,统计成功后,给定单词就可快速找到出现的次数,单词与其出现次数就是<word,count>就构成一种键值对。
namespace KV
{template <class K,class V>struct BSTreeNode{struct BSTreeNode* left;struct BSTreeNode* right;K key;V value;BSTreeNode(const K& key,const V& value):key(key),value(value), left(nullptr), right(nullptr){}};template <class K,class V>class BSTree{typedef BSTreeNode<K,V> Node;public:bool Insert(const K& key,const V& value){if (_root == nullptr) {_root = new Node(key,value);return true;}Node* parent = _root;Node* cur = _root;while (cur != nullptr){if (cur->key < key){parent = cur;cur = cur->right;}else if (cur->key > key){parent = cur;cur = cur->left;}elsereturn false;}if (parent->key < key){parent->right = new Node(key,value);}else{parent->left = new Node(key,value);}return true;}Node* Find(const K& key){Node* cur = _root;while (cur != nullptr){if (cur->key < key){cur = cur->right;}else if (cur->key > key){cur = cur->left;}elsereturn cur;}return nullptr;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* _root){if (_root == nullptr)return;_InOrder(_root->left);cout << _root->key << ":"<<_root->value;_InOrder(_root->right);}protected:Node* _root = nullptr;};
}void Test4()
{KV::BSTree<string, int> b;string arr[] = { "苹果","苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
"苹果", "香蕉", "苹果", "香蕉" };for (auto& e : arr){auto ret = b.Find(e);if (ret){ret->value++;}else{b.Insert(e, 1);}}b.InOrder();
}int main()
{Test4();
}
3.二叉搜索树的性能分析
插入和删除操作必须先查找,查找效率代表了二叉搜索树中的各个操作的性能。
对于n个节点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是节点在二叉搜索树的深度的函数,即插入节点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树。

最优情况下:二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数log2Nlog_2Nlog2N
最差情况下,二叉搜索树退化为单支树,其平均比较次数为:N2\frac{N}{2}2N
相关文章:

二叉搜索树
1.二叉搜索树 1.1.二叉搜索树概念 二叉搜索树又称二叉排序树,它或者是一颗空树,或者是具有一下性质的二叉树。 若它的左子树不为空,则左子树上的所有节点的值都小于根节点的值。若它的右子树不为空,则右子树上的所有节点的值都…...
数据结构(三):集合、字典、哈希表
数据结构(三)一、集合(Set)1.封装一个集合类2.集合常见的操作(1)并集(2)交集(3)差集(4)子集二、字典(Map)三、…...

Linux内核驱动开发(一)
Linux内核初探 linux操作系统历史 开发模式 git 分布式管理git clone 获取git push 提交git pull 更新 邮件组 mailing list patch 内核代码组成 Makfile arch 体系系统架构相关 block 块设备 crypto 加密算法 drivers 驱动(85%) atm 通信bluet…...

TCP/IP协议二十问
TCP/IP协议二十问 1. 什么是TCP网络分层? TCP网络分层一般分为五层: 应用层(HTTP):组装数据包传输层(TCP):增加TCP头部,包含端口号等信息网络互联层(IP&am…...

常用Array数组操作方法
定义一个测试数组constplayers[{name:科比,num:24},{name:詹姆斯,num:23},{name:保罗,num:3},{name:威少,num:0},{name:杜兰特,num:35}]复制代码1、forEach参数代表含义item:遍历项index:遍历项的索引arr:数组本身Array.prototype.sx_forEach…...
【C++】set/multiset、map/multimap的使用
目录 一、关联式容器 二、set的介绍 1、接口count与容器multiset 2、接口lower_bound和upper_bound 三、map的介绍 1、接口insert 2、接口insert和operator[]和at 3、容器multimap 四、map和set相关OJ 1、前K个高频单词 2、两个数组的交集 一、关联式容器 vector、…...
vue3语法
vue3教程 //ps 这里是基本写法 一般项目不需要ref 因为需要一直return 这里是根据在不使用ts后缀 来在.vue里面写setup 如下图所示:setup setup是启动页面会自动执行的一个函数 项目里定义的所有变量,都要在setup当中 在setup定义的变量和方法,都需要r…...
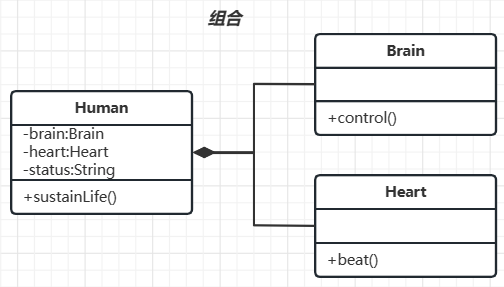
对象之间的关系
目录1. 依赖2. 关联3. 聚合4. 组合Java的对象/类之间有四种关系:依赖、关联、组合、聚合。 1. 依赖 依赖(Dependency): 一个对象的功能依赖于另一个对象。 类比:人类生存依赖食物和空气 体现:被依赖者体…...
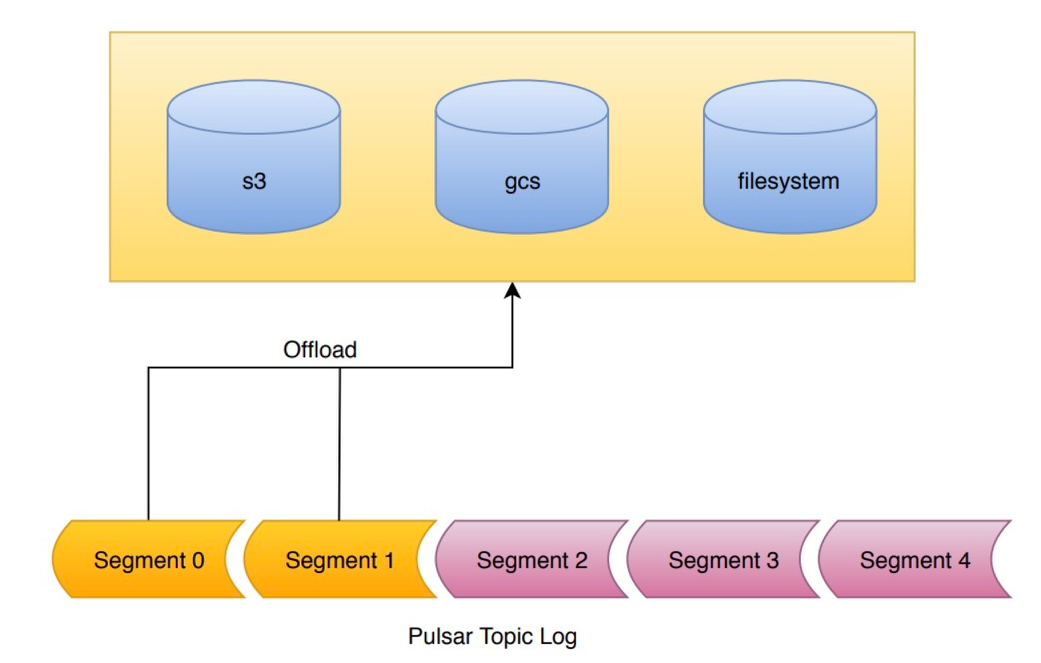
云原生时代顶流消息中间件Apache Pulsar部署实操-上
文章目录安装运行时Java版本推荐Locally Standalone集群启动验证部署分布式集群部署说明初始化集群元数据部署BookKeeper部署BrokerAdmin客户端和验证Tiered Storage(层级存储)概述支持分级存储何时使用工作原理安装 运行时Java版本推荐 Locally Standalone集群 启动 # 下载…...

Python实现基于openCV+百度智能云平台实现《1:N人脸考勤机》文章最后附带源码!
目录 一、 项目介绍 1.1 项目名称 1.2 项目简介 1.3 项目物料 1.4 技术栈 二、 项目架构 三、项目细节 3.1 环境搭建 3.2 利用opencv实现摄像头调取及相关图像的采集 3.3 利用aips上传图像和结果返回 3.4 结果优化和处理 3.5 可扩展性 3.6 遗留问题和…...

因为锁的问题,我们被扣了1万
前言 春节放假期间,一个项目上的积分接口被刷,而且不止一个人在刷,并且东西也被兑走,放假晚上被人叫起来排查问题,通过这个人的积分明细观察,基本一秒就能获取一次,远远超过了积分规则限定的次…...
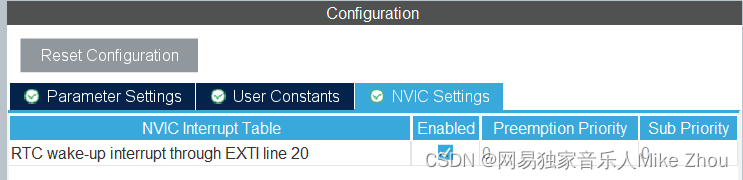
【STM32笔记】低功耗模式下的RTC唤醒(非闹钟唤醒,而是采用RTC_WAKEUPTIMER)
【STM32笔记】低功耗模式下的RTC唤醒(非闹钟唤醒,而是采用RTC_WAKEUPTIMER) 前文: blog.csdn.net/weixin_53403301/article/details/128216064 【STM32笔记】HAL库低功耗模式配置(ADC唤醒无法使用、低功耗模式无法烧录…...

浏览器渲染中的相关概念
渲染 渲染流水线 构建 DOM 树 输入:HTML 文档;处理:HTML 解析器解析;输出:DOM 数据解构。 样式计算 输入:CSS 文本;处理:属性值标准化,每个节点具体样式(…...

【MySQL】数据类型
1、数据类型描述 类型类型举例整数类型TINYINT、SMALLINT、MEDIUMINT、INT(或INTEGER)、BIGINT浮点类型FLOAT、DOUBLE定点数类型DECIMAL位类型BIT日期时间类型YEAR、TIME、DATE、DATETIME、TIMESTAMP文本字符串类型CHAR、VARCHAR、TINYTEXT、TEXT、MEDIUMTEXT、LONGTEXT枚举类…...

L2-037 包装机
一种自动包装机的结构如图 1 所示。首先机器中有 N 条轨道,放置了一些物品。轨道下面有一个筐。当某条轨道的按钮被按下时,活塞向左推动,将轨道尽头的一件物品推落筐中。当 0 号按钮被按下时,机械手将抓取筐顶部的一件物品&#x…...
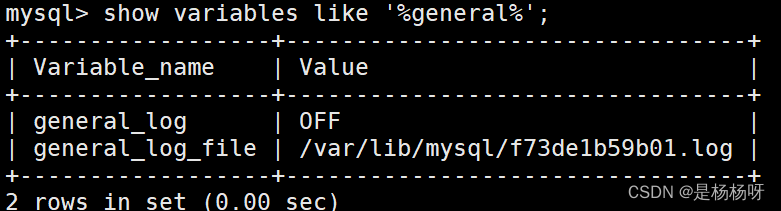
MySQL -查询日志、二进制日志、错误日志、慢查询日志
文章目录1.错误日志2.二进制日志3.查询日志4.慢查询日志1.错误日志 错误日志是 MySOL中最重要的日志之一,它记录了当 mvsald 启动和停止时,以及服务器在运行过程中发生任何严重错误时的相关信息当数据库出现任何故障导致无法正常使用时,建议…...

TCP实现可靠传输的实现
TCP实现可靠传输的实现 目录TCP实现可靠传输的实现ARQ协议停止等待协议(古老)连续ARQ协议累计重传(回退N帧的ARQ协议)缓存确认(选择重传ARQ协议)超时重传的时间选择TCP的流量控制零窗口探测报文段Nagle算法…...

2/14考试总结
时间安排 7:30–7:50 看题,T1可能是个数据结构之类的东西,T2是 dp ,T3 构造。 7:50–8:20 T3,仿照样例的构造,可以通过一部分测试点。 8:20–9:20 T1,发现题目实际上要求子树内各儿子的深度信息,可以 dsu ,对于不能暴…...

程序环境和预处理详解
文章目录一、程序环境1.1 - 翻译环境1.1.1 - 编译1.1.1.1 - 预编译(预处理)1.1.1.2 - 编译1.1.1.3 - 汇编1.1.2 - 链接1.2 - 执行环境二、预处理详解2.1 - 预定义符号2.2 - #define2.2.1 - #define 定义标识符2.2.1.1 - 语法2.2.1.2 - 建议2.2.2 - #defi…...

The Social-Engineer Toolkit(社会工程学工具包)互联网第一篇全模块讲解
一、工具介绍 Social-Engineer Toolkit 是一个专为社会工程设计的开源渗透测试框架,可以帮助或辅助你完成二维码攻击、可插拔介质攻击、鱼叉攻击和水坑攻击等。SET 本身提供了大量攻击选项,可让您快速进行信任型攻击,也是一款高度自定义工具…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...