树的存储和遍历
文章目录
- 6.5 树与森林
- 6.5.1 树的存储结构
- 1. 双亲表示法(顺序存储结构)
- 2 孩子链表表示法
- 3 孩子兄弟表示法(二叉树表示法)
- 6.5.2 森林与二叉树的转换
- 1 树转换成二叉树
- 2 二叉树转换成树
- 3 森林转换成二叉树
- 4 二叉树转换成森林
- 6.5.3 树和森林的遍历
- 1. 树的遍历
- 2. 森林的遍历
- 6.6 赫夫曼树及其应用
- 6.6.1 最优二叉树(Huffman树)
- 1 基本概念
- 2 Huffman树的构造
- 6.6.2 赫夫曼编码及其算法
- 1. Huffman编码
- 2. Huffman编码算法实现
6.5 树与森林
本节将讨论树的存储结构、树及森林与二叉树之间的相互转换、树的遍历等。
6.5.1 树的存储结构
树的存储结构根据应用的不同而不同。
1. 双亲表示法(顺序存储结构)
#define MAX_SIZE 100
typedef struct PTNode
{ElemType data;int parent;
} PTNode;
根据该数据结构的定义,PTNode 是 “Parent Tree Node” 的缩写,即“双亲树节点”。在双亲树中,每个节点在存储自己的数据的同时,也存储了其父节点在数组中的位置。
typedef struct
{PTNode Nodes[MAX_SIZE];int root; /* 根结点位置 */int num; /* 结点数 */
} Ptree;
图6-13所示是一棵树及其双亲表示的存储结构。这种存储结构利用了任一结点的父结点唯一的性质。可以方便地直接找到任一结点的父结点,但求结点的子结点时需要扫描整个数组。

2 孩子链表表示法
树中每个结点有多个指针域,每个指针指向其一棵子树的根结点。其实这么说有点绕口,其实就是每个指针指向
(1) 定长结点结构
指针域的数目就是树的度。
其特点是:链表结构简单,但指针域的浪费明显。结点结构如图6-14(a) 所示。在一棵有 n n n 个结点,度为 k k k 的树中必有 n ( k − 1 ) + 1 n(k-1)+1 n(k−1)+1 空指针域。
(2) 不定长结点结构
树中每个结点的指针域数量不同,是该结点的度,如图6-14(b) 所示。没有多余的指针域,但操作不便。

(3) 复合链表结构
n n n 个结点的树有 n n n 个单链表(叶子结点的孩子链表为空),而 n n n 个头结点又组成一个线性表且以顺序存储结构表示。

#define MAX_NODE 100
typedef struct listnode
{int childno; /* 孩子结点编号 */struct listno *next;
} CTNode; /* 表结点结构 */typedef struct
{ElemType data;CTNode *firstchild;
} HNode; /* 头结点结构 */typedef struct
{HNode nodes[MAX_NODE];int root; /* 根结点位置 */int num; /* 结点数 */
} CLinkList; /* 头结点结构 */
CTNode是 “Child Next Node” 的缩写
CLinkList是 “Child Linked List” 的缩写,即“孩子链表”。它是一种树的链式存储结构

图6-13所示的树T的孩子链表表示的存储结构如图6-16所示。
(考试可能会考,给同学们一棵树,画出若干种表示方法)
3 孩子兄弟表示法(二叉树表示法)
(最重要的表示方法,考试常考)
以二叉链表作为树的存储结构,其结点形式如图6-17(a)所示。

两个指针域:分别指向结点的第一个子结点和下一个兄弟结点。结点类型定义如下:
typedef struct CSnode
{ElemType data;struct CSnode *firstchild, *nextsibing;
} CSNode;
CSNode 是 “Child Sibling Node” 的缩写,即“孩子-兄弟节点” 。在以孩子-兄弟表示法存储树或森林时,每个节点包含一个指向它的第一个孩子节点和下一个兄弟节点的指针,称为孩子-兄弟节点。
6.5.2 森林与二叉树的转换
由于二叉树和树都可用二叉链表作为存储结构,对比各自的结点结构可以看出,以二叉链表作为媒介可以导出树和二叉树之间的一个对应关系。
◆ 从物理结构来看,树和二叉树的二叉链表是相同的,只是对指针的逻辑解释不同而已。
◆ 从树的二叉链表表示的定义可知,任何一棵和树对应的二叉树,其右子树一定为空。
图6-18直观地展示了树和二叉树之间的对应关系。

1 树转换成二叉树
对于一般的树,可以方便地转换成一棵唯一的二叉树与之对应。将树转换成二叉树在“孩子兄弟表示法”中已给出,其详细步骤是:
- 加虚线。在树的每层按从“左至右”的顺序在兄弟结点之间加虚线相连。
- 去连线。除最左的第一个子结点外,父结点与所有其它子结点的连线都去掉。
- 旋转。原有的实线左斜。
- 整型。将旋转后树中的所有虚线改为实线,并向右斜。该转换过程如图6-19所示。
这样转换后的二叉树的特点是:
◆ 二叉树的根结点没有右子树,只有左子树;
◆ 左子结点仍然是原来树中相应结点的左子结点,而所有沿右链往下的右子结点均是原来树中该结点的兄弟结点。

2 二叉树转换成树
对于一棵转换后的二叉树,如何还原成原来的树? 其步骤是:
-
加虚线。若某结点 i i i 是其父结点的左子树的根结点,则将该结点 i i i 的右子结点以及沿右子链不断地搜索所有的右子结点,将所有这些右子结点与 i i i 结点的父结点之间加虚线相连,如图6-20(a)所示。
-
去连线。去掉二叉树中所有父结点与其右子结点之间的连线,如图6-20(b)所示。
-
整型。将图中各结点按层次排列且将所有的虚线变成实线,如图6-20(c)所示。

3 森林转换成二叉树
当一般的树转换成二叉树后,二叉树根节点的右子树必为空。若把森林中的第二棵树(转换成二叉树后)的根结点作为第一棵树(二叉树)的根结点的兄弟结点,则可导出森林转换成二叉树的转换算法如下。
设 F = { T 1 , T 2 , ⋯ , T n } F=\{T_1, T_2,⋯,T_n\} F={T1,T2,⋯,Tn} 是森林,则按以下规则可转换成一棵二叉树 B = ( root , LB , RB ) B=(\operatorname{root},\operatorname{LB},\operatorname{RB}) B=(root,LB,RB)
① 若 $F=\varnothing $,则 B B B 为空树
② 若 F F F 非空,即 n ≠ 0 n\ne 0 n=0,则 B B B 的根 r o o t root root 即为森林中第一棵树的根 r o o t ( T 1 ) root(T_1) root(T1);而其右子树 R B RB RB 是从森林 F ’ = { T 2 , T 3 , ⋯ , T n } F’=\{T_2, T_3,⋯,T_n\} F’={T2,T3,⋯,Tn} 转换而成的二叉树。
4 二叉树转换成森林
若 B = ( r o o t , L B , R B ) B=(root,LB,RB) B=(root,LB,RB) 是一棵二叉树,则可以将其转换成由若干棵树构成的森林: F = { T 1 , T 2 , ⋯ , T n } F=\{T_1, T_2,⋯,T_n\} F={T1,T2,⋯,Tn} 。
转换算法:
① 若 B B B 是空树,则 F F F 为空。
② 若 B B B 非空,则 F F F 中第一棵树 T 1 T_1 T1 的根 r o o t ( T 1 ) root(T_1) root(T1) 就是二叉树的根 r o o t root root, T 1 T_1 T1 中根结点的子森林 F 1 F1 F1 是由树 B B B 的左子树 L B LB LB 转换而成的森林; F F F 中除 T 1 T_1 T1 外其余树组成的的森林 F ’ = { T 2 , T 3 , ⋯ , T n } F’=\{T_2, T_3,⋯,T_n\} F’={T2,T3,⋯,Tn} 是由 B B B 右子树 R B RB RB 转换得到的森林。
上述转换规则是递归的,可以写出其递归算法。以下给出具体的还原步骤。
6.5.3 树和森林的遍历
1. 树的遍历
由树结构的定义可知,树的遍历有二种方法。
- 先序遍历:先访问根结点,然后依次先序遍历完每棵子树。如图6-23的树,先序遍历的次序是:
A B C D E F G I J H K ABCDEFGIJHK ABCDEFGIJHK - 后序遍历:先依次后序遍历完每棵子树,然后访问根结点。如图6-23的树,后序遍历的次序是:
C D B F I J G H E K A CDBFIJGHEKA CDBFIJGHEKA

说明:
◆ 树的先序遍历实质上与将树转换成二叉树后对二叉树的先序遍历相同。
◆ 树的后序遍历实质上与将树转换成二叉树后对二叉树的中序遍历相同。
对于一般的树而言,并没有明显的左右子树之分,因此在树上定义中序遍历并不合理。对于一般的树,我们主要考虑先遍历根节点还是遍历子树。
其实树的先序遍历实质上与将树转换成二叉树后对二叉树的先序遍历逻辑上是很好理解的,根节点是没有右子树的。那么二叉树实际上逻辑理解就是,先访问根结点,然后访问他的其余子树。对于有右节点的子树的根,根左右可以理解成先访问根,然后访问根下的那棵树,最后再去访问子树森林中的其他树。这样的逻辑结果就和树的遍历中的先序遍历完全一致了。
2. 森林的遍历
设 F = { T 1 , T 2 , ⋯ , T n } F=\{T_1, T_2,⋯,T_n\} F={T1,T2,⋯,Tn} 是森林,对 F F F 的遍历有二种方法。
⑴ 先序遍历:按先序遍历树的方式依次遍历 F F F 中的每棵树。
⑵ 中序遍历:按中序遍历树的方式依次遍历 F F F 中的每棵树。
6.6 赫夫曼树及其应用
赫夫曼(Huffman)树又称最优树,是一类带权路径长度最短的树,有着广泛的应用。
6.6.1 最优二叉树(Huffman树)
1 基本概念
① 结点路径:从树中一个结点到另一个结点的之间的分支构成这两个结点之间的路径。
② 路径长度:结点路径上的分支数目称为路径长度。
③ 树的路径长度:从树根到每一个结点的路径长度之和。
例图6-23的树。 A A A 到 F F F :结点路径 A E F AEF AEF ;路径长度(即边的数目) 2 2 2 ;树的路径长度: 3 × 1 + 5 × 2 + 2 × 3 = 19 3\times 1+5\times2+2\times3=19 3×1+5×2+2×3=19

④ 结点的带权路径长度:从该结点的到树的根结点之间的路径长度与结点的权(值)的乘积。
⑤ 树的带权路径长度:树中所有叶子结点的带权路径长度之和,记做:
W P L = w 1 × l 1 + w 2 × l 2 + ⋯ + w n × l n = ∑ w i × l i ( i = 1 , 2 , ⋯ , n ) W P L=w_{1} \times l_{1}+w_{2} \times l_{2}+\cdots+w_{n} \times l_{n}=\sum w_{i} \times l_{i} \quad(i=1,2, \cdots, n) WPL=w1×l1+w2×l2+⋯+wn×ln=∑wi×li(i=1,2,⋯,n)
其中: n n n 为叶子结点的个数; w i w_i wi为第 i i i 个结点的权值; l i l_i li 为第 i i i 个结点的路径长度。
⑥ Huffman树:具有 n n n 个叶子结点(每个结点的权值为 w i w_i wi) 的二叉树不止一棵,但在所有的这些二叉树中,必定存在一棵 W P L WPL WPL 值最小的树,称这棵树为 Huffman 树(或称最优树) 。
在许多判定问题时,利用 Huffman 树可以得到最佳判断算法。如图6-24是权值分别为 2 、 3 、 6 、 7 2、3、6、7 2、3、6、7,具有 4 4 4 个叶子结点的二叉树,它们的带权路径长度分别为:
( a ) W P L = 2 × 2 + 3 × 2 + 6 × 2 + 7 × 2 = 36 ( b ) W P L = 2 × 1 + 3 × 2 + 6 × 3 + 7 × 3 = 47 ( c ) W P L = 7 × 1 + 6 × 2 + 2 × 3 + 3 × 3 = 34 \begin{aligned} &(a) WPL =2 \times 2+3 \times 2+6 \times 2+7 \times 2=36 \\ &(b) WPL=2 \times 1+3 \times 2+6 \times 3+7 \times 3=47 \\ &(c) W P L=7 \times 1+6 \times 2+2 \times 3+3 \times 3=34 \\ \end{aligned} (a)WPL=2×2+3×2+6×2+7×2=36(b)WPL=2×1+3×2+6×3+7×3=47(c)WPL=7×1+6×2+2×3+3×3=34
其中(c)的 W P L WPL WPL 值最小,可以证明是 Huffman 树。

2 Huffman树的构造
① 根据 n n n 个权值 { w 1 , w 2 , ⋯ , w n } \{w_1, w_2, ⋯,w_n\} {w1,w2,⋯,wn},构造成 n n n 棵二叉树的集合 F = { T 1 , T 2 , ⋯ , T n } F=\{T_1, T_2, ⋯,T_n\} F={T1,T2,⋯,Tn},其中每棵二叉树只有一个权值为 w i w_i wi 的根结点,没有左、右子树;
② 在 F F F 中选取两棵根结点权值最小的树作为左、右子树构造一棵新的二叉树,且新的二叉树根结点权值为其左、右子树根结点的权值之和;
③ 在 F F F 中删除这两棵树,同时将新得到的树加入F中;
④ 重复②、③,直到F只含一颗树为止。
构造 Huffman 树时,为了规范,规定 F = { T 1 , T 2 , ⋯ , T n } F=\{T_1, T_2, ⋯,T_n\} F={T1,T2,⋯,Tn} 中权值小的二叉树作为新构造的二叉树的左子树,权值大的二叉树作为新构造的二叉树的右子树;在取值相等时,深度小的二叉树作为新构造的二叉树的左子树,深度大的二叉树作为新构造的二叉树的右子树。
图6-25是权值集合 W = { 8 , 3 , 4 , 6 , 5 , 5 } W=\{8, 3, 4, 6, 5, 5\} W={8,3,4,6,5,5} 构造 Huffman 树的过程。所构造的 Huffman 树的 WPL 是:
W P L = 6 × 2 + 3 × 3 + 4 × 3 + 8 × 2 + 5 × 3 + 5 × 3 = 79 \mathrm{WPL}=6 \times 2+3\times 3+4\times 3+8\times 2+5\times 3+5\times 3 =79 WPL=6×2+3×3+4×3+8×2+5×3+5×3=79
6.6.2 赫夫曼编码及其算法
课本P147页
1. Huffman编码
在电报收发等数据通讯中,常需要将传送的文字转换成由二进制字符0、1组成的字符串来传输。为了使收发的速度提高,就要求电文编码要尽可能地短 。此外,要设计长短不等的编码,还必须保证任意字符的编码都不是另一个字符编码的前缀 ,这种编码称为前缀编码。
Huffman树可以用来构造编码长度不等且译码不产生二义性的编码。
设电文中的字符集 C = { c 1 , c 2 , ⋯ , c i , ⋯ , c n } C=\{c_1,c_2, ⋯,c_i, ⋯,c_n\} C={c1,c2,⋯,ci,⋯,cn},各个字符出现的次数或频度集 W = { w 1 , w 2 , ⋯ , w i , ⋯ , w n } W=\{w_1,w_2, ⋯,w_i, ⋯,w_n\} W={w1,w2,⋯,wi,⋯,wn}。
从根结点到每个叶子结点所经历的路径分支上的“0”或“1”所组成的字符串,为该结点所对应的编码,称之为 Huffman 编码。
若字符集 C = { a , b , c , d , e , f } C=\{a, b, c, d, e, f\} C={a,b,c,d,e,f} 所对应的权值集合为 W = { 8 , 3 , 4 , 6 , 5 , 5 } W=\{8, 3, 4, 6, 5, 5\} W={8,3,4,6,5,5},如图6-25所示,则字符 a , b , c , d , e , f a,b, c,d, e,f a,b,c,d,e,f 所对应的 Huffman 编码分别是: 10 , 010 , 011 , 00 , 110 , 111 10,010,011,00 ,110,111 10,010,011,00,110,111。

2. Huffman编码算法实现
(1) 数据结构设计
Huffman 树中没有度为 1 的结点。若有 n n n 个叶子结点的 Huffman 树共有 2 n − 1 2n-1 2n−1 个结点,则可存储在大小为 2 n − 1 2n-1 2n−1 的一维数组中。实现编码的结点结构如图6-26所示。

#define MAX_NODE 200 /* Max_Node>2n-1 */
typedef struct
{unsigned int Weight; /* 权值域 */unsinged int Parent, Lchild, Rchild;
} HTNode,*HuffmanTree;//动态分配数组存储H树typedef char **HuffmanCode;//动态分配数组存储
(2) Huffman树的生成
算法实现
void Create_Huffman(unsigned n, HuffmanTree &HT[])
/* 创建一棵叶子结点数为n的Huffman树 */
{unsigned int w;m=2*n;int k, j;for (k = 1; k < m; k++){if (k <= n){ printf(“\n Please Input Weight : w=?”);scanf(“% d”, &w);HT[k].weight = w;} /* 输入时,所有叶子结点都有权值 */elseHT[k].weight = 0; /* 非叶子结点没有权值 */HT[k].Parent = HT[k].Lchild = HT[k].Rchild = 0;} /* 初始化Huffman树 HT */for (k = n + 1; k < m; k++){unsigned int w1 = 32767, w2 = w1;/* w1 , w2分别保存权值最小的两个权值 */int p1 = 0, p2 = 0;/* p1 , p2保存两个最小权值的下标 */for (j = 1; j <= k - 1; j++){if (HT[j].Parent == 0) /* 尚未合并 */{/*默认w1是最小的权值*/if (HT[j].Weight < w1){w2 = w1;p2 = p1;w1 = HT[j].Weight;p1 = j;}else if (HT[j].Weight < w2){w2 = HT[j].Weight;p2 = j;}} /* 找到权值最小的两个值及其下标 */}HT[k].Lchild = p1;HT[k].Rchild = p2;HT[k].weight = w1 + w2;HT[p1].Parent = k;HT[p2].Parent = k;}
}
说明:生成 Huffman 树后,树的根结点的下标是 2 n − 1 2n-1 2n−1,即 m − 1 m-1 m−1 。
(3) Huffman编码算法
根据出现频度(权值) Weight,对叶子结点的Huffman 编码有两种方式:
① 从叶子结点到根逆向处理,求得每个叶子结点对应字符的 Huffman 编码。
② 从根结点开始遍历整棵二叉树,求得每个叶子结点对应字符的 Huffman 编码。
算法实现
void Huff_coding(unsigned n, Hnode HT[],Huffmancode &HC)
/* m应为n+1,编码的最大长度n加1 */
{int k, sp, fp, m = n + 1;char *cd, *HC[m];cd = (char *)malloc(n * sizeof(char)); /* 动态分配求编码的工作空间 */cd[n] =‘\0’; /* 编码的结束标志,不加容易出乱码 */for (k = 1; k < n + 1; k++) /* 逐个求字符的编码 */{sp = n;for (p = k, fp = HT[k].parent; fp != 0; p = fp, fp = HT[p].parent)/* 在一次循环中,fp指向的是父结点,p 指向的是当前结点*//* 从叶子结点到根逆向求编码 */if (HT[fp].parent == p)cd[--sp] =‘0’;elsecd[--sp] =‘1’;HC[k] = (char *)malloc((n - sp) * sizeof(char));/* 为第k个字符分配保存编码的空间 */trcpy(HC[k], &cd[sp]);}free(cd);
}
课本P154例子非常重要。
相关文章:

树的存储和遍历
文章目录 6.5 树与森林6.5.1 树的存储结构1. 双亲表示法(顺序存储结构)2 孩子链表表示法3 孩子兄弟表示法(二叉树表示法) 6.5.2 森林与二叉树的转换1 树转换成二叉树2 二叉树转换成树3 森林转换成二叉树4 二叉树转换成森林 6.5.3 树和森林的遍历1. 树的遍历2. 森林的遍历 6.6 赫…...

MySQL的ID用完了,怎么办?
目 录 一 首先首先分情况 二 自增ID 1 mysql 数据库创建一个自增键的表 2 导出表结构 3 重新创建 自增键是4294967295的表 4 查看表结构 5 异常测试 三 填充主键 1 首先创建一个test 表,主键不自增 2 插入主键最大值 3 再次插入主键最大值1 四 没有声明…...
)
JSP基于Iptables图形管理工具的设计与实现(源代码+论文)
Netfilter/Iptables防火墙是Linux平台下的包过滤防火墙,Iptables防火墙不仅提供了强大的数据包过滤能力,而且还提供转发,NAT映射等功能,是个人及企业级Linux用户构建网络安全平台的首选工具。但是,由于种种原因&#x…...

什么是数据库分片?
什么是数据库分片? 数据库分片是指将一个大型数据库拆分成多个小型数据库,每个小型数据库称为一个分片。通过这种方式,可以将数据库的负载分散到多个服务器上,从而提高数据库的性能和可伸缩性。 为什么需要数据库分片?…...
软件工程知识点
软件工程提出的时代和背景 软件工程化的层次 软件开发过程 敏捷与计划开发 演化式开发和DevOps 软件配置管理过程和相关工具名 软件质量和代码异味 能够分析常见的代码异味和bug 代码复杂度和计算圈复杂度 了解代码异味和重构行为的关系 了解自动化单元测试框架xunit…...
)
华为OD机试 - 投篮大赛(Python)
题目描述 你现在是一场采用特殊赛制投篮大赛的记录员。这场比赛由若干回合组成,过去几回合的得分可能会影响以后几回合的得分。 比赛开始时,记录是空白的。 你会得到一个记录操作的字符串列表 ops,其中ops[i]是你需要记录的第i项操作,ops遵循下述规则: 整数x-表示本回合…...

《花雕学AI》讯飞星火认知大模型的特点和优势,与ChatGPT的对比分析
引言: 人工智能是当今科技领域的热门话题,自然语言处理是人工智能的重要分支。自然语言处理的目标是让计算机能够理解和生成自然语言,实现人机交互和智能服务。近年来,随着深度学习的发展,自然语言处理领域出现了许多创…...

【Python入门】Python的判断语句(if else 语句)
前言 📕作者简介:热爱跑步的恒川,致力于C/C、Java、Python等多编程语言,热爱跑步,喜爱音乐的一位博主。 📗本文收录于Python零基础入门系列,本专栏主要内容为Python基础语法、判断、循环语句、函…...
【大数据新闻速递】数字中国峰会成功举办;“浙江数据知识产权登记平台”上线;贵州大数据活跃;AI教父从谷歌离职)
(4.28-5.4)【大数据新闻速递】数字中国峰会成功举办;“浙江数据知识产权登记平台”上线;贵州大数据活跃;AI教父从谷歌离职
01【2023年数字中国建设峰会数字福建分论坛成功举办】 2023年数字中国建设峰会数字福建分论坛由福建省人民政府主办,福建省数字福建建设领导小组办公室、数字中国研究院(福建)和福建省大数据集团承办。分论坛于2023年4月28日下午14:30 -17:3…...
之建立领域模型)
领域驱动设计(Domain Driven Design)之建立领域模型
文章目录 用领域模型表达领域概念建立模型使用通用语言验证模型识别构造块类型设计聚合如何使用领域模型再次思考总结用领域模型表达领域概念 在实际项目中,模型设计者往往过早陷入具体构造块类型的识别,比如实体、聚合、领域服务,而忽略了领域模型表达领域概念的目的。我们…...

有研究员公开了一个解析并提取 Dell PFS BIOS 固件的工具(下)
导语:研究员公开了一个解析并提取 Dell PFS BIOS 固件的工具。 Apple EFI IM4P分配器 介绍 解析苹果多个EFI固件.im4p文件,并将所有检测到的EFI固件分割为单独的SPI/BIOS映像。 使用 你可以拖放或手动输入包含Apple EFI IM4P固件的文件夹的完整路径。…...

iOS开发系列--Swift语言
概述 Swift是苹果2014年推出的全新的编程语言,它继承了C语言、ObjC的特性,且克服了C语言的兼容性问题。Swift发展过程中不仅保留了ObjC很多语法特性,它也借鉴了多种现代化语言的特点,在其中你可以看到C#、Java、Javascript、Pyth…...

【MOMO】高水平期刊目录(持续更新)
高水平期刊目录 引言1 顶级期刊目录(A)1.1 IEEE Transactions on Intelligent Transportation Systems1.2 IEEE Transactions on Neural Networks and Learning Systems1.3 Engineering 2 权威期刊目录(A)2.1 Measurement 3 鼓励期…...

LVS负载均衡集群--DR模式
一、LVS-DR集群介绍 LVS-DR(Linux Virtual Server Director Server)工作模式,是生产环境中最常用的一 种工作模式。 1、LVS-DR 工作原理 LVS-DR 模式,Director Server 作为群集的访问入口,不作为网关使用࿰…...
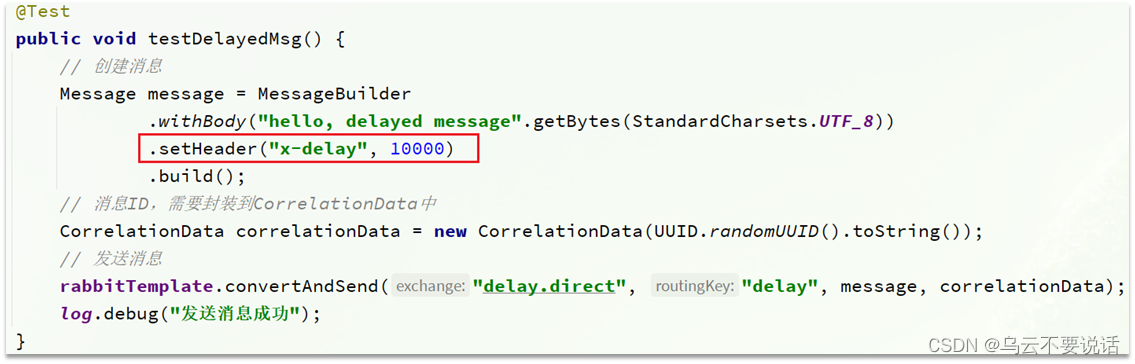
RabbitMQ --- 死信交换机
一、简介 1.1、什么是死信交换机 什么是死信? 当一个队列中的消息满足下列情况之一时,可以成为死信(dead letter): 消费者使用basic.reject或 basic.nack声明消费失败,并且消息的requeue参数设置为false…...
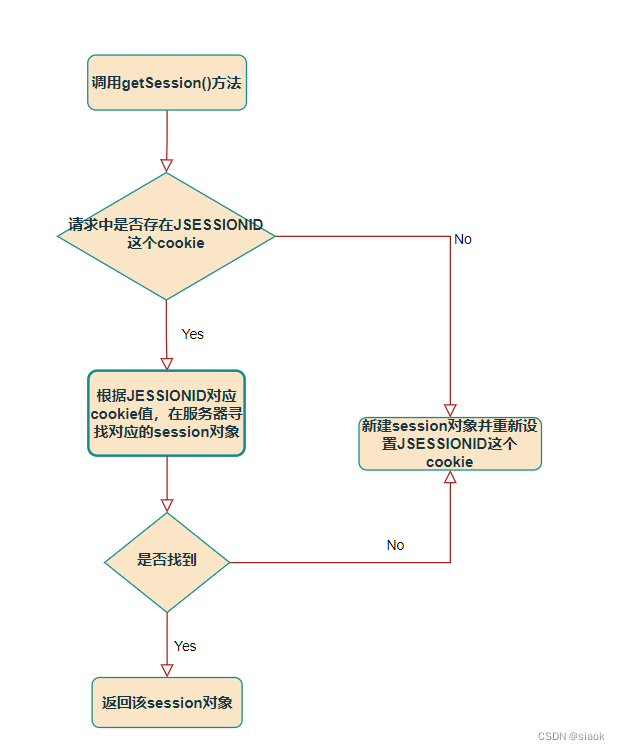
如何在个人web项目中使用会话技术(cookiesession)?
编译软件:IntelliJ IDEA 2019.2.4 x64 操作系统:win10 x64 位 家庭版 服务器软件:apache-tomcat-8.5.27 目录 一. 什么是会话?二. 为什么要使用会话技术?三. 如何使用会话技术?3.1 Cookie(客户端的会话技术…...
创建线索二叉树
创建线索二叉树 一、创建线索二叉树一、案例1、前序线索二叉树2、中序线索二叉树3、后序线索二叉树 一、创建线索二叉树 现将某结点的空指针域指向该结点的前驱后继,定义规则如下: 若结点的左子树为空,则该结点的左孩子指针指向其前驱结点。…...
HNU-操作系统OS-实验Lab2
OS_Lab2_Experimental report 湖南大学信息科学与工程学院 计科 210X wolf (学号 202108010XXX) 前言 实验一过后大家做出来了一个可以启动的系统,实验二主要涉及操作系统的物理内存管理。操作系统为了使用内存,还需高效地管理…...

如何使用HTML和CSS创建有方向感知的按钮
在互联网应用中,按钮是一种常见的控件,用户通过点击按钮来触发相应的操作。考虑到用户体验和交互设计,设计有方向感知的按钮可以使得用户更加易于理解按钮的功能和状态。 在本文中,我们将介绍如何使用HTML和CSS来创建具有方向感知…...

java 线程安全
内部锁 在 Java 中,每个对象都有一个内部锁,也称为监视器锁或对象锁。内部锁是通过在代码块或方法前加上 synchronized 关键字来实现的。当一个线程执行一个带有 synchronized 关键字的方法或代码块时,它必须先获得该对象的内部锁࿰…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...
