P1054 [NOIP2005 提高组] 等价表达式
题目描述
明明进了中学之后,学到了代数表达式。有一天,他碰到一个很麻烦的选择题。这个题目的题干中首先给出了一个代数表达式,然后列出了若干选项,每个选项也是一个代数表达式,题目的要求是判断选项中哪些代数表达式是和题干中的表达式等价的。
这个题目手算很麻烦,因为明明对计算机编程很感兴趣,所以他想是不是可以用计算机来解决这个问题。假设你是明明,能完成这个任务吗?
这个选择题中的每个表达式都满足下面的性质:
- 表达式只可能包含一个变量 �a。
- 表达式中出现的数都是正整数,而且都小于 1000010000。
- 表达式中可以包括四种运算 ++(加),--(减),**(乘),^^(乘幂),以及小括号 ((,))。小括号的优先级最高,其次是 ^^,然后是 **,最后是 ++ 和 --。++ 和 -- 的优先级是相同的。相同优先级的运算从左到右进行。(注意:运算符 ++,--,**,^^ 以及小括号((,)) 都是英文字符)
- 幂指数只可能是 11 到 1010 之间的正整数(包括 11 和 1010)。
- 表达式内部,头部或者尾部都可能有一些多余的空格。
下面是一些合理的表达式的例子:
((a^1) ^ 2)^3,a*a+a-a,((a+a)),9999+(a-a)*a,1 + (a -1)^3,1^10^9………
输入格式
第一行给出的是题干中的表达式。
第二行是一个整数 �n,表示选项的个数。后面�n行,每行包括一个选项中的表达式。这 �n 个选项的标号分别是 �,�,�,�⋯A,B,C,D⋯
输入中的表达式的长度都不超过 5050 个字符,而且保证选项中总有表达式和题干中的表达式是等价的。
输出格式
一行,包括一系列选项的标号,表示哪些选项是和题干中的表达式等价的。选项的标号按照字母顺序排列,而且之间没有空格。
输入输出样例
输入 #1复制
( a + 1) ^2 3 (a-1)^2+4*a a + 1+ a a^2 + 2 * a * 1 + 1^2 + 10 -10 +a -a
输出 #1复制
AC
说明/提示
- 对于 30%30% 的数据,表达式中只可能出现两种运算符 ++ 和 --;
- 对于其它的数据,四种运算符 ++,--,**,^^ 在表达式中都可能出现。
- 对于 100%100% 的数据,表达式中都可能出现小括号 (( 和 )),2≤�≤262≤n≤26。
【题目来源】
NOIP 2005 提高组第四题
余观此题,未生特殊代值之意,徒有多项式运算之情。所以然者何?变量单一,形式有限,假一数组,以次数顺列系数,则神形兼备,功能俱全。遂写结构,用重载。又用栈,以计算。
说明白点,就是直接拿个结构体,用多项式每项前的系数存成一个数组,来表示多项式,然后通过重载运算符来支持多项式的各种运算。但这里有个问题,就是a的最高次数可能远远超过10。事实上,有一个测试点的数据就有
(a -6)^10^10
所以多项式数组的大小不能只开到11。但这样的话,这个数组岂不是要开的非常大?然而既然可以用代特殊值的方法来做,我以为,算一下目标和结果的“较低”次数也可以管中窥豹略见一斑。即:如果两个多项式在�N次以内的系数都相等,并且�N足够大的时候,也可以判定两个多项式是相等的。这里�N取到100就可以过这题了,也不会出现TLE的问题。这个题解之前没有考虑溢出的问题,最近经过评论区提醒,系数数组需要开long long。
但严格来说,将系数对大数(如1e9+7)取模是更严谨的做法。这种做法另一个问题就是代码量比较大,可能需要比较长的编码调试时间。这个思路主要优势是比较直观,也容易想到。另外写的这个struct非常实用。print()稍微完善一下,或者不完善,因为也能看懂,这已经可以用来做数学作业啦!
(原题解发布于2018-09-24,2021-02-25更新)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<vector>
#include<stack>
#include<string>
#define N 100
using namespace std; struct poly{long long p[N+2];void clear(){memset(p, 0, sizeof(p));}poly operator= (const poly &b){this->clear();for (int i=0; i<=N; i++) p[i]=b.p[i];return *this;}poly operator= (const int b){this->clear();p[0]=b;return *this;}poly operator+ (const poly &b) const{poly c;for (int i=0; i<=N; i++){c.p[i]=p[i]+b.p[i];}return c;}poly operator- (const poly &b) const{poly c;for (int i=0; i<=N; i++){c.p[i]=p[i]-b.p[i];}return c;}poly operator* (const poly &b) const {poly c;c.clear();for (int i=0; i<=N; i++){for (int j=0; j<=N; j++){if (i+j>N) continue;int k=i+j;c.p[k]+=p[i]*b.p[j];}}return c;}poly pow(const poly &b) const {//b must be an integer.int t=b.p[0];poly ans; ans=1;poly pas; pas=(*this);while (t){if (t&1) {ans=ans*pas;}pas=pas*pas;t>>=1;}return ans;}void print(){for (int i=N; i>=0; i--){if (p[i]==0) continue;if (i!=N) cout<<'+';cout<<p[i]<<"a^"<<i;}cout<<endl;}bool operator== (const poly&b) const {for (int i=0; i<=N; i++){if (p[i]!=b.p[i]) return false;}return true;}};stack<poly> s1;
stack<char> s2;inline int f(char c){if (c=='^') return 3;if (c=='*' ) return 2;if (c=='+' || c=='-') return 1;else return 0;
}inline void js(){poly a, b; char c;poly ans;b=s1.top(); s1.pop();a=s1.top(); s1.pop();c=s2.top(); s2.pop();if (c=='+') ans=a+b;if (c=='-') ans=a-b;if (c=='*') ans=a*b;if (c=='^') ans=a.pow(b);s1.push(ans);
}const char L[18]="0123456789+-*^a()";inline bool legal(char c){for (int i=0; i<17; i++){if (c==L[i]) return true; }return false;
}inline poly read(){string s;getline(cin, s);int len=s.size();int judge=0; bool ok=1;if (s.empty()) ok=0;for (int i=0; i<len; i++){if (s[i]=='(') judge++;if (s[i]==')') judge--;if (judge<0) ok=0;}if (judge>0) ok=0;if (!ok) {poly wrong; wrong.clear(); wrong.p[N+1]=1; return wrong;}//gets(s);bool flag=0; int temp=0; poly pt;poly a; a.clear(); a.p[1]=1;for (int i=0; i<len; i++){char &n=s[i];if (!legal(n)) continue;if (n=='a') {s1.push(a); continue;}if (n>='0' && n<='9') {temp=(temp<<1)+(temp<<3)+n-'0'; flag=1; continue;}if (flag) {pt=temp; s1.push(pt); temp=0; flag=0;}if (n=='(') {s2.push(n); continue;}if (n==')') {while (s2.top()!='(') js();s2.pop();continue;}while (!s2.empty() && f(s2.top())>=f(n)) js();s2.push(n);}if (flag) {pt=temp; s1.push(pt);}while (!s2.empty()) js();poly res=s1.top();s1.pop();return res;//s1.top().print();
}int main(){poly aim; aim=read();//aim.print();int n; scanf("%d\n", &n); for (int i=0; i<n; i++){poly now=read();//now.print();if (now==aim) {char c='A'+i; cout<<c;}}cout<<endl; return 0;
}
相关文章:

P1054 [NOIP2005 提高组] 等价表达式
题目描述 明明进了中学之后,学到了代数表达式。有一天,他碰到一个很麻烦的选择题。这个题目的题干中首先给出了一个代数表达式,然后列出了若干选项,每个选项也是一个代数表达式,题目的要求是判断选项中哪些代数表达式…...

什么牌子蓝牙耳机好用不贵?国产性价比高的蓝牙耳机推荐
相较于有线耳机,无线蓝牙耳机更便携、功能更丰富,不用受到耳机孔与线的限制。那么,什么牌子的蓝牙耳机好用不贵?针对这个问题,我给大家推荐几款国产性价比高的蓝牙耳机,可以当个参考。 一、南卡小音舱Lite…...

明明花钱上了ERP,为什么还要我装个MES系统
目前, ERP系统依旧是很多制造企业的选择。据统计,ERP系统的应用已经达到70%以上,但是在车间的应用, MES系统的应用比例并不高。那么,为什么现在很多企业又都选择再上个MES呢? MES系统是一个面向…...

JAVA中的集合框架有哪些?
在Java中,集合(Collection)是一组对象的容器,而集合框架(Collection Framework)是一组接口、实现类和算法,用于存储和操作集合。Java集合框架提供了一组通用的、高性能的、可扩展的接口和类&…...
用Jmeter进行接口自动化测试的工作流程你知道吗?
目录 测试流程 接口测试相关文档管理规范 接口测试要点 测试流程 在测试负责人接受到测试任务后,应该按照以下流程规范完成测试工作。 2.1 测试需求分析 产品开发负责人在完成某产品功能的接口文档编写后,在核对无误后下发给对应的接口测试负责人…...
)
Java 中的设计模式有哪些?(十九)
Java设计模式是一套被反复使用、多数人知晓的、经过分类编目的、代码设计经验的总结。 设计模式可以帮助我们解决软件开发过程中面临的一般问题,提高代码的可读性、可复用性和可扩展性。 Java中一般认为有23种设计模式,总体来说设计模式分为三大类&…...

奇数单增序列
题目描述 给定一个长度为 N(不大于 500)的正整数序列,请将其中的所有奇数取出,并按升序输出。 输入格式 第 1 行为 N;第 2 行为 N 个正整数,其间用空格间隔。 输出格式 增序输出的奇数序列,…...
Seata介绍
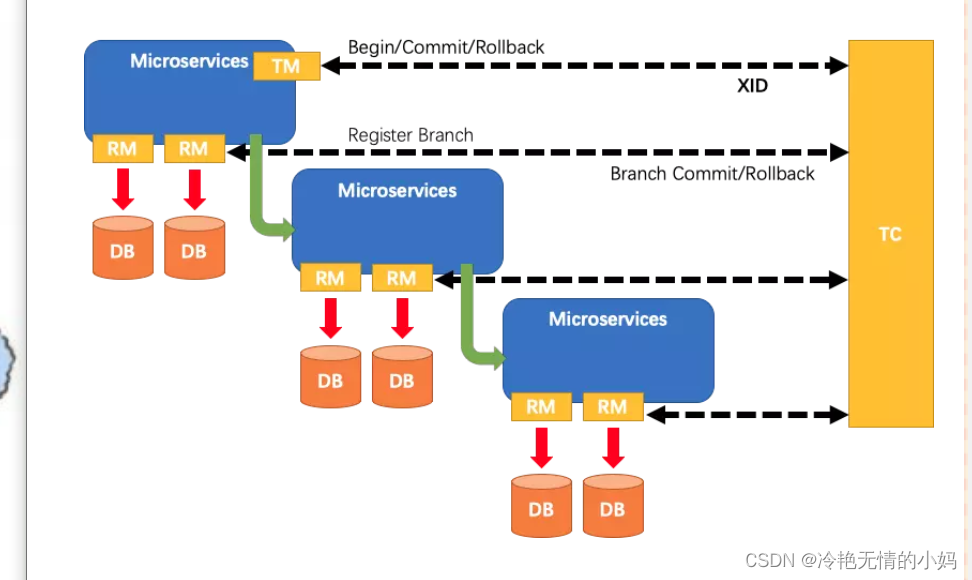
介绍: Seata的设计目标是对这个业务无侵入,因此从业务无侵入的2PC方案开始的,在传统的2PC的基础上演进的。它把一个分布式事务拆分理解成一个包含了若干分支事务的全局事务。全局事务的职责是协调其下管辖的分支事务达成一致性,要…...
VK Cup 2017 - Round 1 A - Bear and Friendship Condition(并查集维护大小 + dfs 遍历图统计边数)
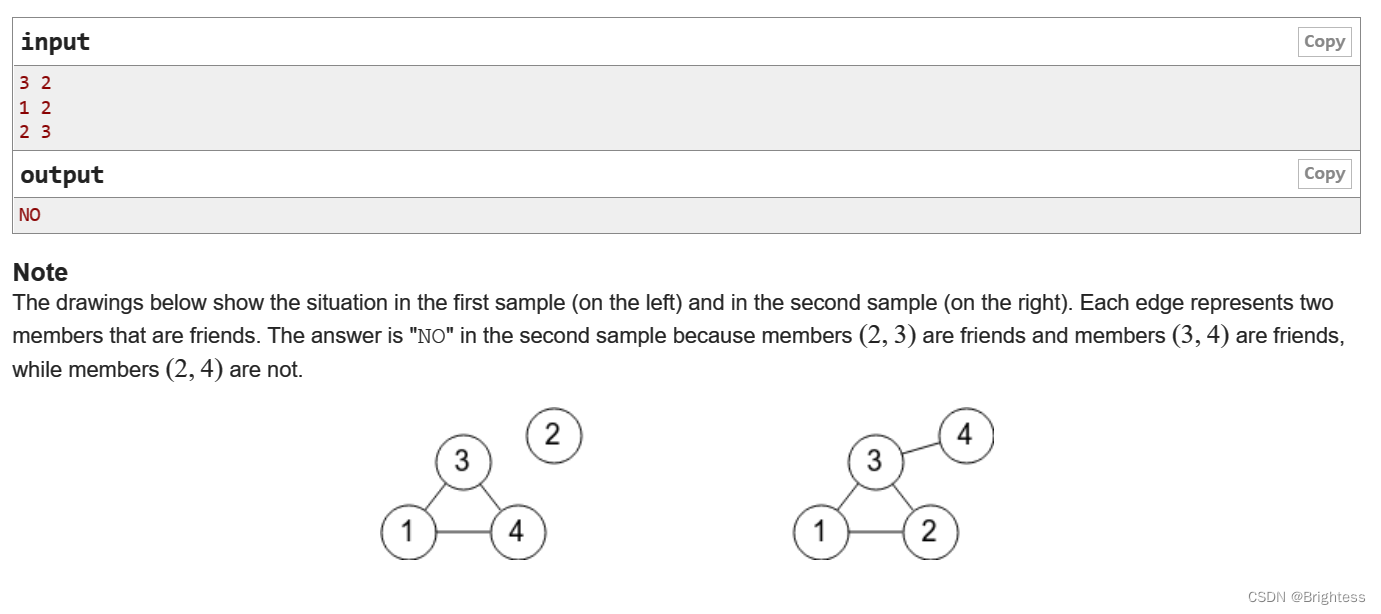
题目大意: 给你一些n个点m条边,如果三个点(a,b,c)是合法的,当且仅当 a-b,b-c,c-a都有一条边,问你这个图是否合法,如果有一个或两个点视为合法 思路 考虑什么图才是个合法图:除了点…...

为UOS启用VNC和Windows远程桌面
1 参考资料 UOS系统中安装x11vnc远程桌面 如何通过windows电脑远程UOS桌面RDP 已在ARM版本和X86版本中验证均可用 2 准备工作 2.1 设置代理(可选) 如果设备本身能和公网通,就不需要了。 由于我们全程需要在root账号下进行,系…...
-- LocalDateTime()类)
Java时间类(七)-- LocalDateTime()类
目录 1. LocalDateTime的概述: 2. LocalDateTime的常用方法: 1. LocalDateTime的概述: 是一个不可变的日期-时间对象,表示日期和时间,而没有时区。 它基于ISO-8601日历系统,是由日期和时间组合而成。它可以存储到纳秒级精度,并提供了各种方法来处理日期和时间的运算…...

卢北辰:数据点亮梦想,能力驱动人生 | 提升之路系列(九)
导读 为了发挥清华大学多学科优势,搭建跨学科交叉融合平台,创新跨学科交叉培养模式,培养具有大数据思维和应用创新的“π”型人才,由清华大学研究生院、清华大学大数据研究中心及相关院系共同设计组织的“清华大学大数据能力提升项…...
数据库基础及用户管理授权
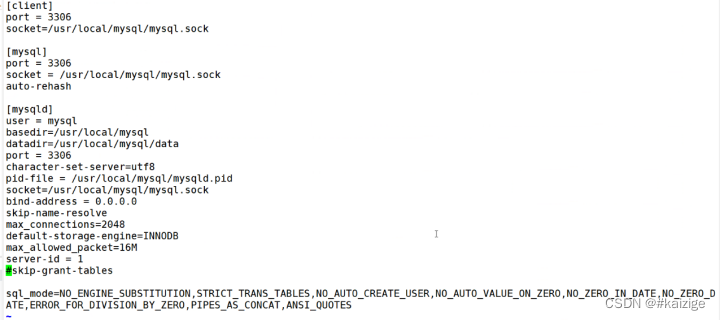
数据库概念 关系型数据库 数据结构二维表格 库 -> 表 -> 列(字段):用来描述对象的的一个属性;行:用来描述一个对象的信息 mysql(5.7/8.0) maridb ocracle postgresql sqlserver(windows…...
比特米盒子刷安卓ATV6.0
最近海鲜市场有很多比特米盒子,50多块包邮,买来的盒子回来折腾下,买回来发现一直卡在“系统启动"中无法进入,不知道原来的是啥系统,看来只能找找线刷的办法,重新拯救救个这盒子。 原文链接地址&#x…...
【用python的QT做信号处理的界面】
文章目录 入口文件界面参数调整数据从dat解析出来的文件从界面点击打开文件夹的功能实现主要功能代码网络参数存图替换功能,比如把倒频谱替换成倒频谱2 入口文件 入口文件,主要用来实例化窗口(不重要),只要知道从这里…...
【Linux】进程间通信 —— 管道
文章目录 📕 进程间通信介绍📕 匿名管道原理使用读写规则特点 📕 命名管道原理使用匿名管道和命名管道的区别 📕 进程间通信介绍 进程间通信,顾名思义,就是两个进程之间的 “交流” ,我们知道&…...

知识管理在企业中的重要性
随着经济全球化和信息化的快速发展,企业面临着越来越多的竞争和挑战。如何把握市场动态、满足客户需求、提高产品质量和效率等,成为了企业发展中亟待解决的问题。而知识管理作为一种新兴的管理方式,逐渐引起了企业们的重视。本文将从以下几个…...

Socks5、网络安全、代理IP技术详解
随着互联网的发展,网络安全问题越来越受到人们的关注。为了保护个人隐私和网络安全,使用代理服务器成为了一种普遍的选择。其中,Socks5协议是一种常见的代理协议,而代理IP是使用代理服务器时经常需要考虑的问题。本文将深入探讨So…...

C++学习day--09 字符串比较、运算符
1、项目练习 第 1 节 项目需求、项目实现 项目实现: #include <iostream> #include <Windows.h> #include <string> using namespace std; int main( void ) { string name; string pwd; std::cout << " 请输入账号&am…...
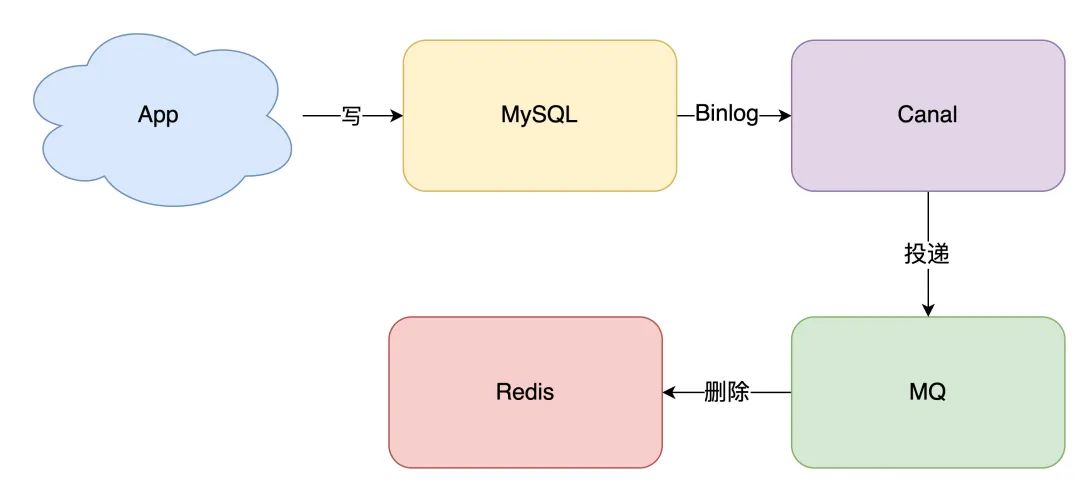
缓存和数据库一致性问题
如何保证缓存和数据库一致性,这是一个老生常谈的话题了。 但很多人对这个问题,依旧有很多疑惑: 到底是更新缓存还是删缓存? 到底选择先更新数据库,再删除缓存,还是先删除缓存,再更新数据库&am…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
