堆及其应用
堆是一种基于树结构的数据结构,通常用于实现优先队列。堆分为最大堆和最小堆两种类型,最大堆的每个节点的值都大于等于其子节点的值,最小堆则相反,每个节点的值都小于等于其子节点的值。
基础算法操作包括:
1. 插入元素:将新元素插入堆的末尾,然后通过上滤操作将其移到正确的位置。
2. 删除堆顶元素:将堆顶元素与堆末尾元素交换,然后将堆末尾元素删除,最后通过下滤操作将堆顶元素移到正确的位置。
3. 上滤操作:将一个新元素插入堆末尾后,将其与其父节点比较,如果大于等于父节点,则不需要操作;否则将其与父节点交换,然后继续向上比较,直到达到堆顶或者不需要交换为止。
4. 下滤操作:将堆顶元素与其子节点比较,如果小于等于子节点,则不需要操作;否则将其与子节点中较大(或较小)的那个交换,然后继续向下比较,直到达到堆底或者不需要交换为止。
5. 建堆操作:将一个无序序列转化为堆的过程,可以通过从最后一个非叶子节点开始进行下滤操作,直到堆顶。
以下是基于数组实现的最小堆,包括插入元素、删除堆顶元素、上滤操作、下滤操作和建堆操作的实现。
应用场景:
堆是一种数据结构,具有动态分配内存、动态扩容等特点,在计算机科学中有许多应用场景。以下是堆的几个应用场景:
1. 内存管理
堆常用于动态分配内存,例如在程序运行时需要创建一个动态数组,但是数组的大小在编译时是未知的,这时可以使用堆来动态分配内存。C语言中的malloc和free函数就是堆的常见应用。
2. 优先队列
堆可以用来实现优先队列,即队列中的元素按照某种优先级排序,每次取出的元素是优先级最高的。堆实现优先队列的时间复杂度为O(logn),比其他实现方式的时间复杂度低,因此在需要高效实现优先队列的场景中,堆是一个常见的选择。
3. 排序算法
堆排序是一种高效的排序算法,它的时间复杂度为O(nlogn),与快速排序、归并排序等常见的排序算法相当。堆排序的基本思路是将待排序的元素构建成一个二叉堆,然后每次取出堆顶的元素,将其放到已排序的序列中,再对剩余的元素重新构建堆。
4. 图算法
在图算法中,堆常用于实现Dijkstra算法和Prim算法。Dijkstra算法是一种求解单源最短路径问题的算法,它通过维护一个距离起点最短的节点集合,不断扩展该集合来求解最短路径。Prim算法是一种求解最小生成树问题的算法,它通过维护一个已经生成的树的节点集合,不断将与该集合相邻的未被访问的节点加入集合中,直到生成一棵最小生成树。
5. 操作系统
堆在操作系统中也有广泛的应用,例如进程管理中的内存分配和释放、虚拟内存管理中的页面置换等。在进程管理中,堆用于动态分配进程的堆内存,以及动态加载和卸载动态链接库。在虚拟内存管理中,堆可以用于实现页面置换算法中的优先队列,以便快速选择需要置换的页面。
```c++
#include <iostream>
#include <vector>using namespace std;class MinHeap {
private:vector<int> heap; // 存储堆的数组// 上滤操作void siftUp(int index) {while (index > 0) {int parent = (index - 1) / 2;if (heap[parent] > heap[index]) {swap(heap[parent], heap[index]);index = parent;} else {break;}}}// 下滤操作void siftDown(int index) {int size = heap.size();while (index * 2 + 1 < size) {int leftChild = index * 2 + 1;int rightChild = index * 2 + 2;int minIndex = leftChild;if (rightChild < size && heap[rightChild] < heap[leftChild]) {minIndex = rightChild;}if (heap[minIndex] < heap[index]) {swap(heap[minIndex], heap[index]);index = minIndex;} else {break;}}}public:// 插入元素void insert(int val) {heap.push_back(val);siftUp(heap.size() - 1);}// 删除堆顶元素void deleteMin() {int size = heap.size();if (size == 0) {return;}heap[0] = heap[size - 1];heap.pop_back();siftDown(0);}// 建堆操作void buildHeap(vector<int>& nums) {heap = nums;int size = heap.size();for (int i = size / 2 - 1; i >= 0; i--) {siftDown(i);}}// 获取堆顶元素int getMin() {return heap.size() == 0 ? -1 : heap[0];}// 获取堆的大小int size() {return heap.size();}// 判断堆是否为空bool empty() {return heap.empty();}
};int main() {MinHeap heap;heap.insert(3);heap.insert(2);heap.insert(1);cout << heap.getMin() << endl; // 1heap.deleteMin();cout << heap.getMin() << endl; // 2heap.insert(0);cout << heap.getMin() << endl; // 0vector<int> nums = {5, 4, 3, 2, 1};heap.buildHeap(nums);while (!heap.empty()) {cout << heap.getMin() << " ";heap.deleteMin();} // 1 2 3 4 5return 0;
}
```
相关文章:

堆及其应用
堆是一种基于树结构的数据结构,通常用于实现优先队列。堆分为最大堆和最小堆两种类型,最大堆的每个节点的值都大于等于其子节点的值,最小堆则相反,每个节点的值都小于等于其子节点的值。 基础算法操作包括: 1. 插入元…...

MySQL数据库备份脚本
PS:此脚本简单易懂,根据实际情况修改个别参数测试后即可使用,如有错误请指出! 1.MySQL数据库备份脚本 #!/bin/bashuser pw ip dateYdate "%Y" date2date "%Y%m%d" date3date "%Y%m%d %H:%M" date…...
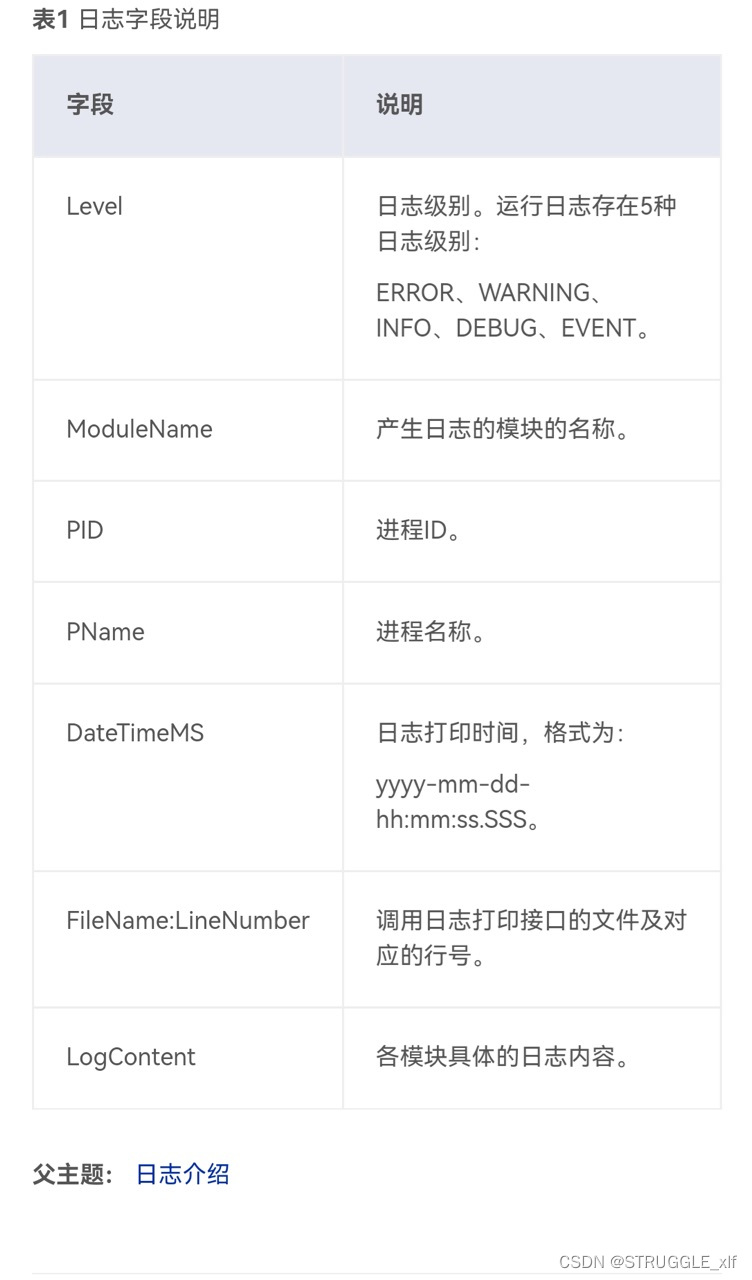
【2023 · CANN训练营第一季】应用开发深入讲解——第三章应用调试
学习资源 日志参考文档 应用开发FAQ 日志主要用于记录系统的运行过程及异常信息,帮助快速定位系统运行过程中出现的问题以及开发过程中的程序调试问题。 日志分为如下两大类: 系统类日志:系统运行产生的日志。主要包括: Contro…...
黎曼几何与黎曼流形
目录 0.黎曼几何 1. 欧几里得几何与黎曼几何的区别 2.黎曼流形 3.黎曼距离 4.切空间 5.黎曼均值 6. SPD矩阵如何形成黎曼流型 7.切线空间映射 8.同余变换和同余不变 9.黎曼对齐 科普性笔记,做了解,不深入。 0.黎曼几何 黎曼几何是一种基于欧几…...

lua | 运算符与字符串
目录 一、运算符 算数运算符 关系运算符 逻辑运算符 其他运算符 运算符优先级 二、字符串 转义字符 方法与用途 字符串截取 字符串大小转换 字符串查找与反转 字符串格式化 字符与整数的转换 匹配模式 本文章为笔者学习分享 学习网站:Lua 基本语法 | …...

NetBackup 10.2 新功能介绍:PostgreSQL 和 MySQL 自动化恢复达成
NetBackup 10.2 新功能介绍:PostgreSQL 和 MySQL 自动化恢复达成 原文来自:VERITAS 中文社区 2023-04-27 在执行恢复任务时,手动提取、更新数据库和实例并将其附加到 PostgreSQL 和 MySQL 是常规操作。而在最新的 NetBackup 10.2 版本中&am…...
ADRV9002官方例程开发过程中遇到的问题
开发环境:Vivado2021.2 HDL版本:hdl_2021_r2 GitHub - analogdevicesinc/hdl at hdl_2021_r2 no-OS版本:no_OS-2021_R2 GitHub - analogdevicesinc/no-OS at 2021_R2 (PS:也可以用Vivado2019.1开发,…...
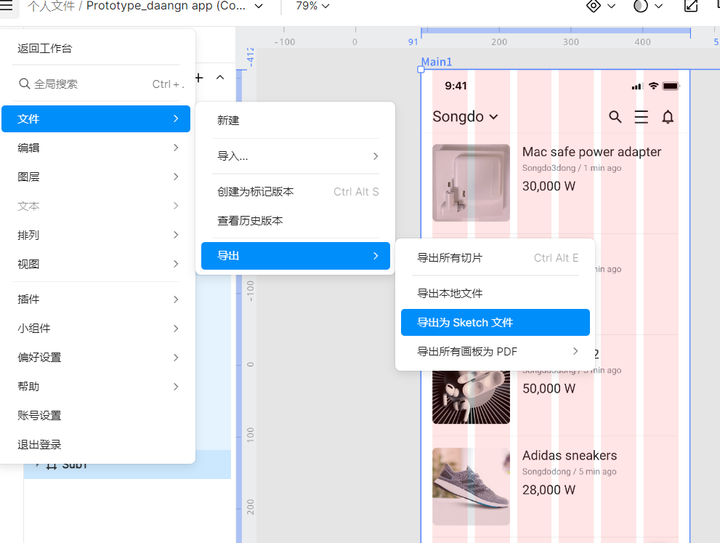
Figma转换为sketch,分享这3款工具
在我们的设计工作中,我们经常会遇到各种各样的设计文件相互转换的问题。 你经常为此头疼吗?当你遇到Figma转换Sketch文件的问题时,你是如何解决的?Figma转换Sketch文件有工具吗? 根据众多设计师的经验,本…...

淘宝天猫1688京东商品详情API接口,封装接口可高并发
要提供商品详情数据需要知道具体的商品信息,但通常商品详情数据应包括以下内容: 商品名称:商品的名称,以方便顾客对其进行识别和区分。 商品描述:一段让顾客能够全面认识商品的描述。应能够有效地展示商品的特性、功能…...
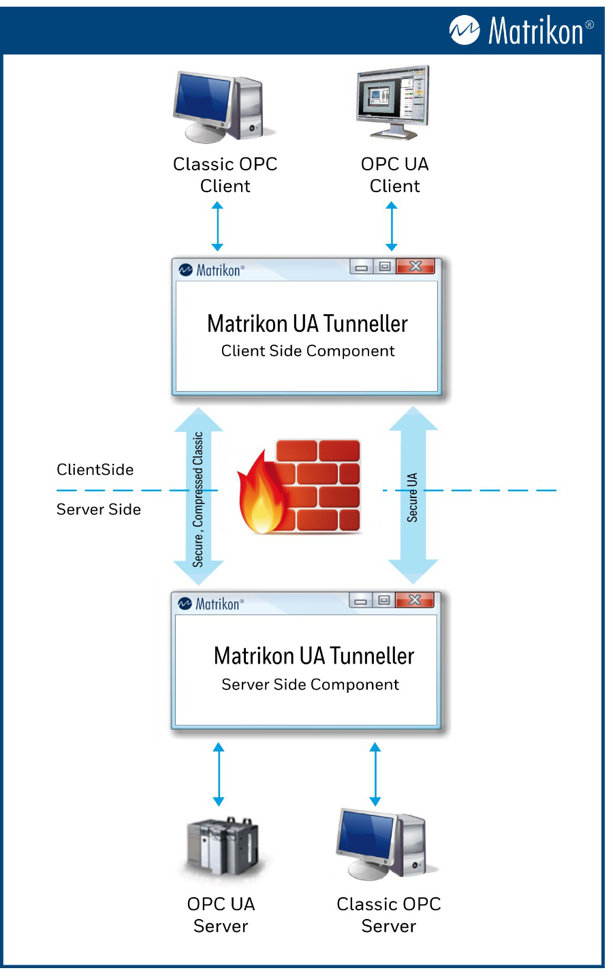
虹科荣誉 | 虹科工业物联网产品荣获中国自动化产业年会用户信赖产品奖!
2023 虹科荣获2021年度中国自动化产业年会用户信赖产品奖 近日,2023中国自动化产业年会于北京隆重举行。虹科工业物联网的产品“OPC UA Tunneller软件”凭借其产品优势和市场美誉度,通过层层选拔,在本次大会中荣获2021年度用户信赖产品奖。…...

SwiftUI 如何让文本自动支持查找和替换功能?
概览 有些情况下,我们需要为文本编辑器实现文本的查找和替换功能(find & replace),如果完全靠自已撸码还是比较棘手的。 所幸的是,从 SwiftUI 4.0 (iOS 16)开始,Apple 已经将查…...
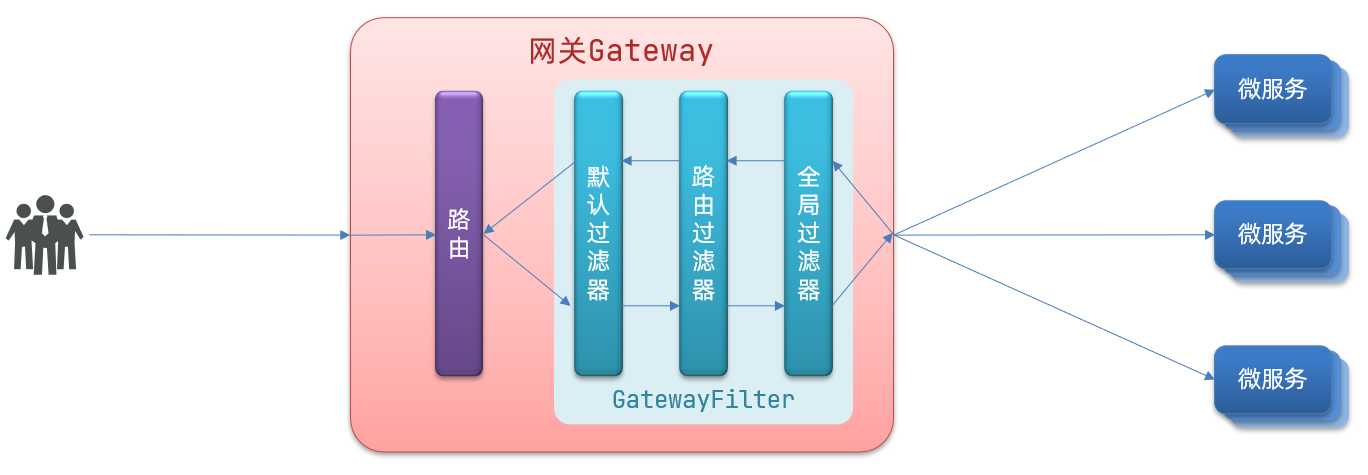
SpringCloud全面学习笔记之初尝美妙篇
目录 前言初识微服务单体架构分布式架构微服务架构初见SpringCloud微服务治理分布式服务架构案例 微服务组件及使用Eureka注册中心提供者和消费者Eureka的结构和作用搭建Eureka服务注册服务服务发现Eureka注册服务总结 Ribbon负载均衡原理负载均衡原理负载均衡策略懒加载 Nacos…...

Spring MVC框架
Spring MVC框架 Spring MVC属于SpringFrameWork的后续产品,已经融合在Spring Web Flow里面。Spring 框架提供了构建 Web 应用程序的全功能 MVC 模块。使用 Spring 可插入的 MVC 架构,从而在使用Spring进行WEB开发时,可以选择使用Spring的Spri…...

Illustrator如何使用图层与蒙版之实例演示?
文章目录 0.引言1.绘制可爱冰淇淋图标2.霓虹渐变立体文字海报3.炫彩花纹背景 0.引言 因科研等多场景需要进行绘图处理,笔者对Illustrator进行了学习,本文通过《Illustrator CC2018基础与实战》及其配套素材结合网上相关资料进行学习笔记总结,…...

Office Tool Plus的使用
是否为安装,卸载,激活Office而烦恼? 下载 地址:Office Tool Plus 官方网站 - 一键部署 Office 安装office 先安装Office,Office_Pro_Plus_2021_LTSCProjectVisio_x64_zh_CN_VL_2022-02 注意,要安装批量…...
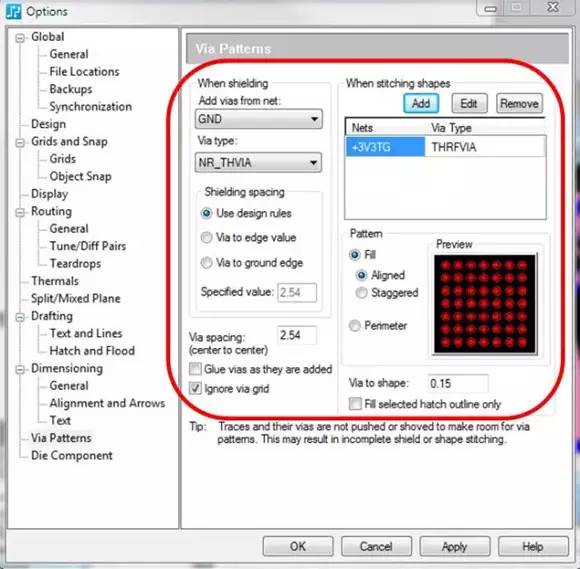
射频PCB 设计的六大条技巧
即使是最自信的设计人员,对于射频电路也往往望而却步,因为它会带来巨大的设计挑战,并且需要专业的设计和分析工具。这里将为您介绍六条技巧,来帮助您简化任何射频PCB 设计任务和减轻工作压力! 1、保持完好、精确的射频…...

优化了成本和安装难度后,UWB信标能否取代蓝牙信标?
1 我们做安U3号是要解决什么问题? (1)信标式设计,解决传统UWB基站安装过程繁琐复杂的问题 传统UWB基站在安装过程中遇上的难题: l 安装位置选取问题:UWB基站的准确度与其安装位置有很大关系,…...

深入理解Java虚拟机——垃圾回收算法
1.前言 垃圾回收需要完成的三件事 首先我们需要明白垃圾回收需要完成的三件事: 哪些内存需要回收 堆内存中的对象所使用的内存方法区中的废弃的常量以及不再使用的类型 什么时候回收 当对象死亡方法区中某些内容(常量和类型)不再被使用 如…...

git-rebase和merge
A-----B----C----D master E----F-----G feature 为了把main分支里新增的代码应用在你的feature分支,你有两种方法:merge 和 rebase。 merge git checkout feature git merge main A-----B----C----D master E----F-----G -----* feature (合并master…...

【JavaWeb 用户认证】Cookie、Session、Token、JWT、Interceptor、SpringBoot、Spring Security
Token基本了解:【详细阐述Token的来源】公钥私钥基本了解:【理解公钥】 文章目录 一、Cookie 经典介绍以及使用案例二、Session 经典介绍以及拦截登录案例三、Token MySQL 的基本介绍及其基本使用四、JWT 基本介绍及其基本讲解五、SpringBoot 使用拦截器…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
