代码随想录算法训练营第五十二天
代码随想录算法训练营第五十二天| 300.最长递增子序列,674. 最长连续递增序列,718. 最长重复子数组
- 300.最长递增子序列
- 674. 最长连续递增序列
- 718. 最长重复子数组
300.最长递增子序列
题目链接:最长递增子序列
这里是不用处理if nums[i] <= nums[j]:的情况的,直接默认了碰到这种情况就直接放弃,有点奇怪,但也说得通。
这样的话其实dp[i]并不是nums[:(i+1)]最长严格递增子序列的长度,而是
以nums[i]为结尾的递增子序列的长度
class Solution:def lengthOfLIS(self, nums: List[int]) -> int:# dp[i] = nums[:(i+1)]最长严格递增子序列的长度dp = [1] * len(nums)for i in range(1,len(nums)):for j in range(i):if nums[i] > nums[j]:dp[i] = max(dp[i],dp[j]+1)#print(dp)return max(dp)
674. 最长连续递增序列
题目链接:最长连续递增序列
和上一题一样这里的dp[i]其实是以nums[i]为结尾的连续递增子序列的长度并不是nums[:(i+1)]里的最长连续递增子序列的长度
class Solution:def findLengthOfLCIS(self, nums: List[int]) -> int:# dp[i] = nums[:(i+1)]中最长且连续递增的子序列dp = [1]*len(nums)for i in range(1,len(nums)):if nums[i] > nums[i-1]:dp[i] = dp[i-1]+1return max(dp)
718. 最长重复子数组
题目链接:最长重复子数组
| i/j | 3 | 2 | 1 | 4 | 7 |
|---|---|---|---|---|---|
| 1 | 1 | ||||
| 2 | 1 | ||||
| 3 | 1 | 1 | |||
| 2 | 2 | ||||
| 1 | 3 |
这个题的顺序是斜着走的,只要能保证左上方是遍历过的就可以了。
class Solution:def findLength(self, nums1: List[int], nums2: List[int]) -> int:#dp[i][j] = nums1[:i]和nums2[:j]的两个数组中公共的长度最长的子数组的长度dp = [[0]*len(nums2) for _ in range(len(nums1))]m = 0for i in range(len(nums1)):if nums1[i] == nums2[0]:dp[i][0] = 1m = 1for j in range(len(nums2)):if nums2[j] == nums1[0]:dp[0][j] = 1m = 1for i in range(1,len(nums1)):for j in range(1,len(nums2)):if nums1[i] == nums2[j]:dp[i][j] = dp[i-1][j-1]+1m = max(dp[i][j],m)#print(dp)#print(m)return m
相关文章:

代码随想录算法训练营第五十二天
代码随想录算法训练营第五十二天| 300.最长递增子序列,674. 最长连续递增序列,718. 最长重复子数组 300.最长递增子序列674. 最长连续递增序列718. 最长重复子数组 300.最长递增子序列 题目链接:最长递增子序列 这里是不用处理if nums[i] &l…...

【Linux网络】传输层中UDP和TCP协议
文章目录 1、再谈端口号2、UDP协议3、TCP协议3.1 TCP协议段格式3.2 TCP的三次握手和四次挥手(连接管理机制)3.3 TCP的滑动窗口3.4 TCP的流量控制3.5 拥塞控制3.6 延迟应答和捎带应答3.7 面向字节流和粘包问题3.8 TCP总结 1、再谈端口号 端口号port标识一…...

工具︱ Web3加密浏览器Brave有什么特别之处?
使用浏览器来上网访问和获取各种信息和资源已经成为传统互联网民的普遍活动,下一代互联网协议Web3的核心特点是去中心化,即不依赖于中心化的服务器和数据中心,而是通过分布式的网络节点来实现数据存储和传输。 浏览器承载着信息网络与用户需求…...

绝对不能错过这份沃尔玛实用插件工具大全
龙哥最近发现很多跨境卖家都比较少运营沃尔玛这个平台。沃尔玛除了是世界500强之外,它的线上商城也弄得很好。它的电商平台主要是售卖自营的,然后你也可以入驻来卖自己的产品,就像是我们国内的京东一样。今天龙哥就给大家分享一些沃尔玛专用插…...

【Java】字符串模板拼接的方法
引 在Java中,构建字符串是非常常见的操作。在很多时候,我们都需要使用变量或输入来定制一个文本输出,例如打印日志、生成HTML代码或构建错误消息。而当需要进行字符串连接时,字符串模板是一种常用的方法。在本篇博客中࿰…...

Vue3项目中使用ECharts图表并实现自适应效果
文章目录 一、Vue3项目安装ECharts二、引入、使用ECharts1.创建图表组件,并在父组件中引入使用2.引入ECharts3.ECharts图表自适应 总结 一、Vue3项目安装ECharts 在项目中输入如下代码: npm install echarts --save安装完成可以在package.json中看到&a…...
快速跑通环信IM Android Demo
1、以Android 4.0.0 Demo为例 https://www.easemob.com/download/demo (下载别的版本的demo 可以修改版本号直接下载就就可以) https://downloadsdk.easemob.com/downloads/easemob-sdk-4.0.0.zip 运行时遇到以下报错在项目build.gradle中添加运行时遇…...
1190 - 1196 题)
leetcode解题思路分析(一百三十九)1190 - 1196 题
反转每对括号间的子串 给出一个字符串 s(仅含有小写英文字母和括号)。请你按照从括号内到外的顺序,逐层反转每对匹配括号中的字符串,并返回最终的结果。注意,您的结果中 不应 包含任何括号。 可以简单的用栈保存当前层…...
PHP+vue基于web的小区物业管理管理系统1995a
小区物业管理系统主要是对小区物业以及居民信息进行管理,方便用户使用该资源的一种有效手段。能有效地对物业以及用户信息进行管理并为广大用户服务是该管理系统的基本要求,同时用户也可以及时了解最新的物业信息,方便地查询相关物业情况。基…...

区间预测 | MATLAB实现QRCNN卷积神经网络分位数回归时间序列区间预测
区间预测 | MATLAB实现QRCNN卷积神经网络分位数回归时间序列区间预测 目录 区间预测 | MATLAB实现QRCNN卷积神经网络分位数回归时间序列区间预测效果一览基本介绍模型描述程序设计参考资料 效果一览 基本介绍 区间预测 | MATLAB实现QRCNN卷积神经网络分位数回归时间序列区间预测…...
【AI 导航网站】为了更好的收集 AI 资源,我开发了一个 AI 导航网站
AI 导航网站 目前 AI 应用正呈迸发式增长,然而一个人获取资源的途径有限,对于目前存在的AI工具不能很好的收集总结,所以基于此,我开发了这个一个AI导航网站,希望通过它,收集出目前存在的热门的AI应用&…...
谈谈HMI 的自动化生成技术
人机界面(HMI)是自动化领域不可或缺重要组成部分。尽管人机界面系统的设计看上去并没有太大的技术门槛,但是设计一个HMI系统的工作量是巨大的。如果你没有足够的耐心便完成不了一个通用的HMI系统。构建UI控件库是一个似乎永远完不成的事情&am…...

docker安装elasticsearch
使用docker部署 部署elasticsearch # 拉取镜像 docker pull elasticsearch# 创建容器 docker run --name es -p 9200:9200 \-p 9300:9300 \-e "discovery.typesingle-node" \-e ES_JAVA_OPTS"-Xms64m -Xmx128m" \-v /home/es/conf/elasticsearch.yml:/…...
)
Docker:使用dockerFile创建镜像(war包和jar包)
1、使用war包打镜像 (1)在war的当前路径下,新建一个文件——Dockerfile (2)编辑Dockerfile文件 vim Dockerfile Dockerfile文件内容: FROM java:8 # 选择项目中要求的版本 MAINTAINER ylb …...
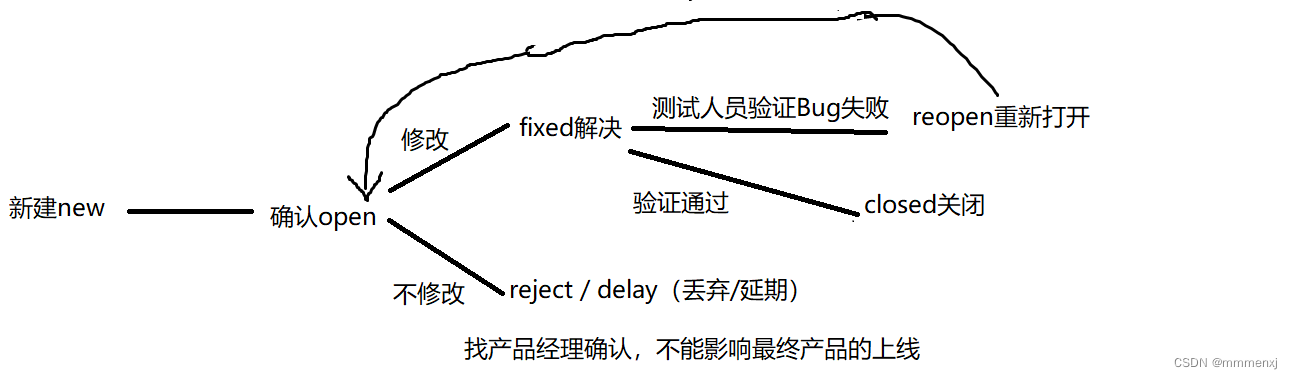
2.基础篇
目录 一、描述软件测试的生命周期(软件测试的流程) 二、如何描述一个bug 三、bug的级别(粗略划分) 四、bug的生命周期 五、因为一个bug和开发人员产生争执怎么办 六、如何设置弱网? 一、描述软件测试的生命周期&a…...
取代你的可能不是AI,而是比你更会使用AI的人
1、背景 从开始了解AI到现在已经1个月了,最明显的就是,产品层出不穷,以前只有技术人员才关系AI,现在各行各业都在关系AI,都希望通过它提高生产力和创造力; 在当今大数据和人工智能时代,职场和企…...

NECCS|全国大学生英语竞赛C类|词汇和语法|语法题|时态 非谓语动词 |19:00~20:15|完形填空·词性转化
14:35~14:45 15:45~16:2019:00~20:15 http://t.csdn.cn/XbsUy 目录 (一)时态 7. 将来进行时 8. 过去将来进行时 9. 现在完成时 10. 过去完成时编辑 11. 将来完成时 12. 现在完成时 13. 过去完成进行时 (…...

【高等数学笔记】Stolz定理
文章目录 Stolz定理 ∗ ∞ \cfrac{*}{\infty} ∞∗型 0 0 \cfrac{0}{0} 00型 例子1. 算术平均数的极限2. Stolz定理可以被理解为“数列的洛必达法则”,它揭示了两个数列之比的极限和相邻两项之差的比的极限的关系。 Stolz定理 ∗ ∞ \cfrac{*}{\infty} ∞∗型…...

【24】核心易中期刊推荐——图像处理研究大数据及智能处理研究
🚀🚀🚀NEW!!!核心易中期刊推荐栏目来啦 ~ 📚🍀 核心期刊在国内的应用范围非常广,核心期刊发表论文是国内很多作者晋升的硬性要求,并且在国内属于顶尖论文发表,具有很高的学术价值。在中文核心目录体系中,权威代表有CSSCI、CSCD和北大核心。其中,中文期刊的数…...
【A、B、C、D】)
Codeforces Round 870 (Div. 2)【A、B、C、D】
文章目录 A. Trust Nobody(暴力)B. Lunatic Never Content(数学)C. Dreaming of Freedom(数学、暴力)D. Running Miles(前缀、后缀) 传送门 A. Trust Nobody(暴力) 题意:给出n个人的陈述,每个人陈述至少有ai个人说谎,让你求出可能是说谎人数…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
