最长递增子序列的长度 _ 贪心+二分查找 _ 20230510
最长递增子序列的长度 _ 贪心+二分查找 _ 20230510
- 前言
最长递增子序列的程序一般采用动态规划方式,使用bottom-up的数组记忆方式比较容易理解,当然也可以采用top-down的递归模式。本文主要讨论如何利用贪心策略,同时辅助以二分查找的方式实现寻找最长递增子序列的长度。
- 问题描述
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,7]是数组[3, 6, 4, 8,7]的子序列。
> >**示例 1:**
输入:nums = [3, 6, 4, 8,7]
输出:3
解释:最长递增子序列是 [3,6,7],因此长度为 3 。
- 贪心策略
如果要获得最长子序列,就需要尾部的元素足够小,同时需要确保执行贪心策略之后,形成的新数组递增有序,由于这两个约束条件同时存在,若设定数组d[i],定义数组的长度len为前i个元素形成的最长子序列的长度。
d[i]数组维护需要涉及到替代操作和尾部插入操作,当原数组中的待考察元素落在当前d[i]的数组区间内,就执行内部替代操作,同时保持d[i]数组长度len保持不变;如果待考察的元素比d[len]值大,那么就进行尾部插入操作,同时数组的长度len增加1。
- 整体算法
首先需要对d[i]数组初始化,并定义其实长度len为1。假定待考察的数组为nums,那么初始化 d[1]=nums[0],根据d[i]数组的单调性,可以采用二分法寻找内部替代的具体位置。假定当前已求出的最长子序列的长度为len,从前往后遍历数组nums,遍历至当前数据元素nums[i]时:
- 如果nums[i]>d[len],则直接插入元素,令d[++len]=nums[i]
- 否则,在d数组中进行二分查找,找到第一个小于nums[i]的数据位置k,并更新d[k+1]=nums[i]
- 过程演示
以nums=[3, 6, 4, 8,7]为例进行示例说明,定义数组d[n+1],数组中储存待维护的元素,数组的长度为截止至下标为i的nums的最长子序列的长度。
第一步操作,进行初始化: dp[1]={3}
第二步操作,插入元素6,由于d[1]<6,所以直接令d[2]=6, d={3,6}
第三步操作,内部替换元素,由于4比d[2]小,所以采用二分法在d中寻找第一个小于4的数据位置k,通过查找k=1,那么更新d[k+1]=d[2]=4, 此时d={3,4}
第四步操作,插入元素8,由于d[2]<8,所以直接在尾部插入元素8,更新d数组,并且数组长度增加1,更新后的d数组为d={3,4,8}
第五步操作,内部元素替换,由于7<d[3],所以采用二分法在d当中寻找第一个小于7的元素位置k,通过查找k=2,更新d数组d={3,4,7}
整个过程完毕后,d数组的长度为3,所以nums数组的最长子序列长度为3,整个流程结束。
- 二分程序实现
程序实现过程中的难点为二分查找方法,这里我们介绍两种实现方式,此两种实现方式差异很小,但是反映了不同的处理思路,
4.1 通过辅助变量定义查找位置
前面我们探讨了k位置查询,实际上k位置要满足的条件为d[k-1]<nums[i]<d[k],它要找的位置为第一个在d数组中小于nums[i]的位置,那么我们可以辅助单变量pos,pos记录这个位置。
对pos初始化为0,处理这样一种情况,如果nums[i]比dp数组中的最小值还要小,那么就需要采用pos的默认值0。
low=1;high=len;pos=0;while(low<=high){mid=(low+high)/2;if (d[mid]<nums[i]){pos=mid;low=mid+1;}else{high=mid-1;}}d[pos+1]=nums[i];}
4.2 通过利用high变量实现
如果仔细研究二分法,就可以看出,辅助变量的位置和high值相等,所以可以在查询结束后,直接采用high的值,此时low>high。
程序实现为:
low=1;high=len;while(low<=high){mid=(low+high)/2;if (d[mid]<nums[i]){low=mid+1;}else{high=mid-1;}}d[high+1]=nums[i];}
- 小结
通过对最长递增子序列的长度的贪心策略回顾,我们使用两种二分查找方式查询带替换元素的位置,加深了对二分查找位置的理解,同时也开阔了最长递增子序列的解题思路。
参考资料:
300. 最长递增子序列 - 力扣(Leetcode)
相关文章:

最长递增子序列的长度 _ 贪心+二分查找 _ 20230510
最长递增子序列的长度 _ 贪心二分查找 _ 20230510 前言 最长递增子序列的程序一般采用动态规划方式,使用bottom-up的数组记忆方式比较容易理解,当然也可以采用top-down的递归模式。本文主要讨论如何利用贪心策略,同时辅助以二分查找的方式实…...

VMware ESXi 7.0 U3m Unlocker OEM BIOS 集成网卡驱动和 NVMe 驱动 (集成驱动版)
ESXi 7 U3 标准版集成 Intel 网卡、USB 网卡 和 NVMe 驱动 请访问原文链接:https://sysin.org/blog/vmware-esxi-7-u3-sysin/,查看最新版。原创作品,转载请保留出处。 作者主页:sysin.org 2023-05-03,发布 ESXi 7.0U…...
Scrum敏捷开发和项目管理流程及工具
Scrum是全球运用最广泛的敏捷管理框架,Leangoo基于Scrum框架提供了一系列的流程和模板,可以帮助敏捷团队快速启动Scrum敏捷开发。 这里可以介绍一下在scrum中单团队敏捷开发如何管理,单团队敏捷开发主要是针对10-15人以下,只有一…...

微服务之配置中心
文章目录 1什么是配置2什么是配置中心3为什么我们要用配置中心4特点 1什么是配置 就是springboot中的application.yml/properties文件 比如:项目名、端口号、数据库连接参数、启动参数等。 2什么是配置中心 配置中心就是用来管理项目当中所有配置的系统ÿ…...
windows下安装OpenCL
由于我的电脑是windows10,显卡是集显Intel UHD Graphics 630。 下载Intel的SDK for OpenCL,下载地址https://software.intel.com/en-us/opencl-sdk/choose-download,也可以在我的资源里面直接下载https://download.csdn.net/download/qq_363…...
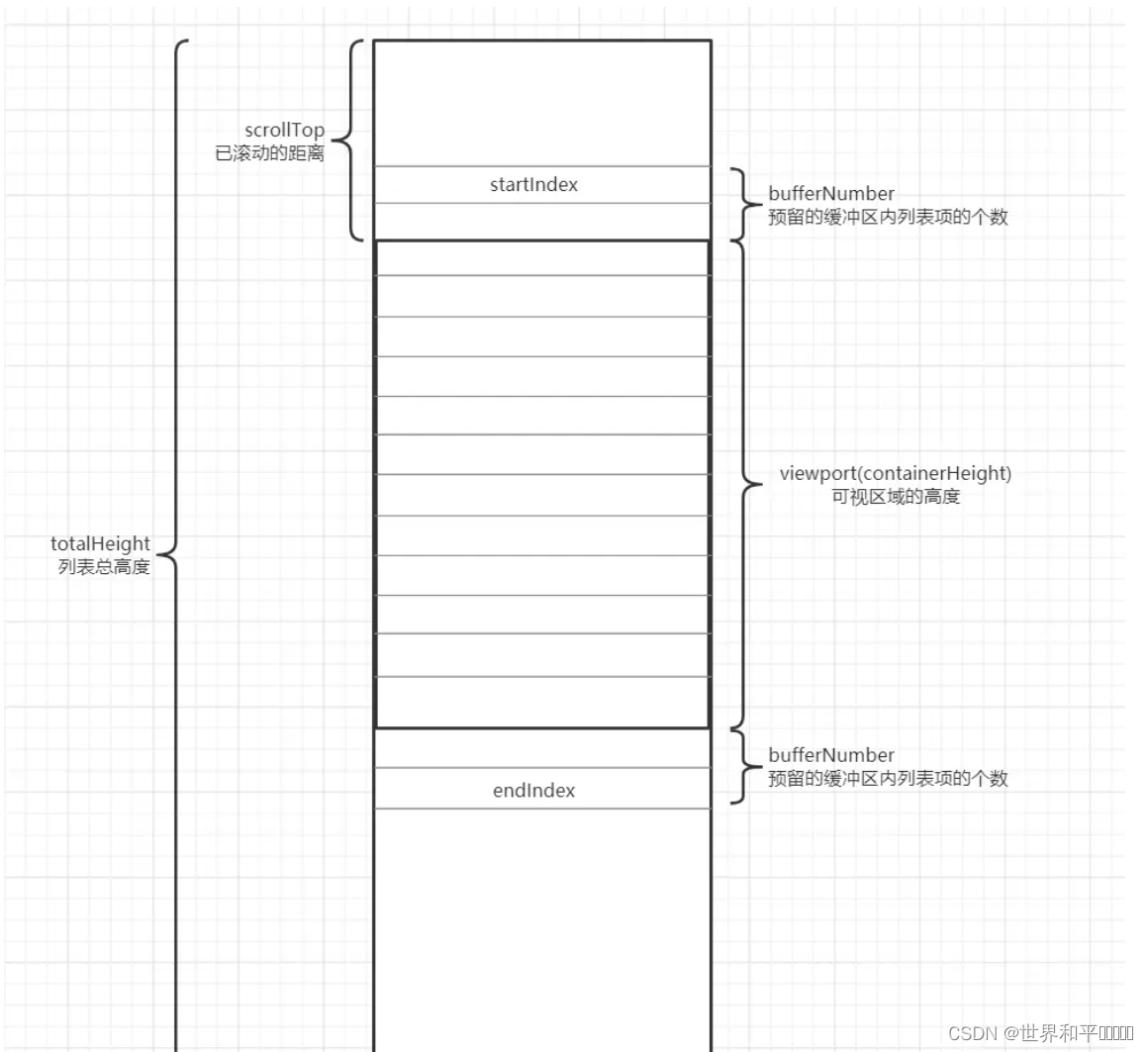
前端项目的通用优化策略
一、虚拟滚动 当我们开发的时候,遇到大数据加载,页面卡顿的问题应该如何处理?大多数情况下,我们都是尽量通过分页的方式处理这类问题,但是总有一些特殊的情况我们必须把数据全部加载到前端进行处理。我曾经遇到过一个…...
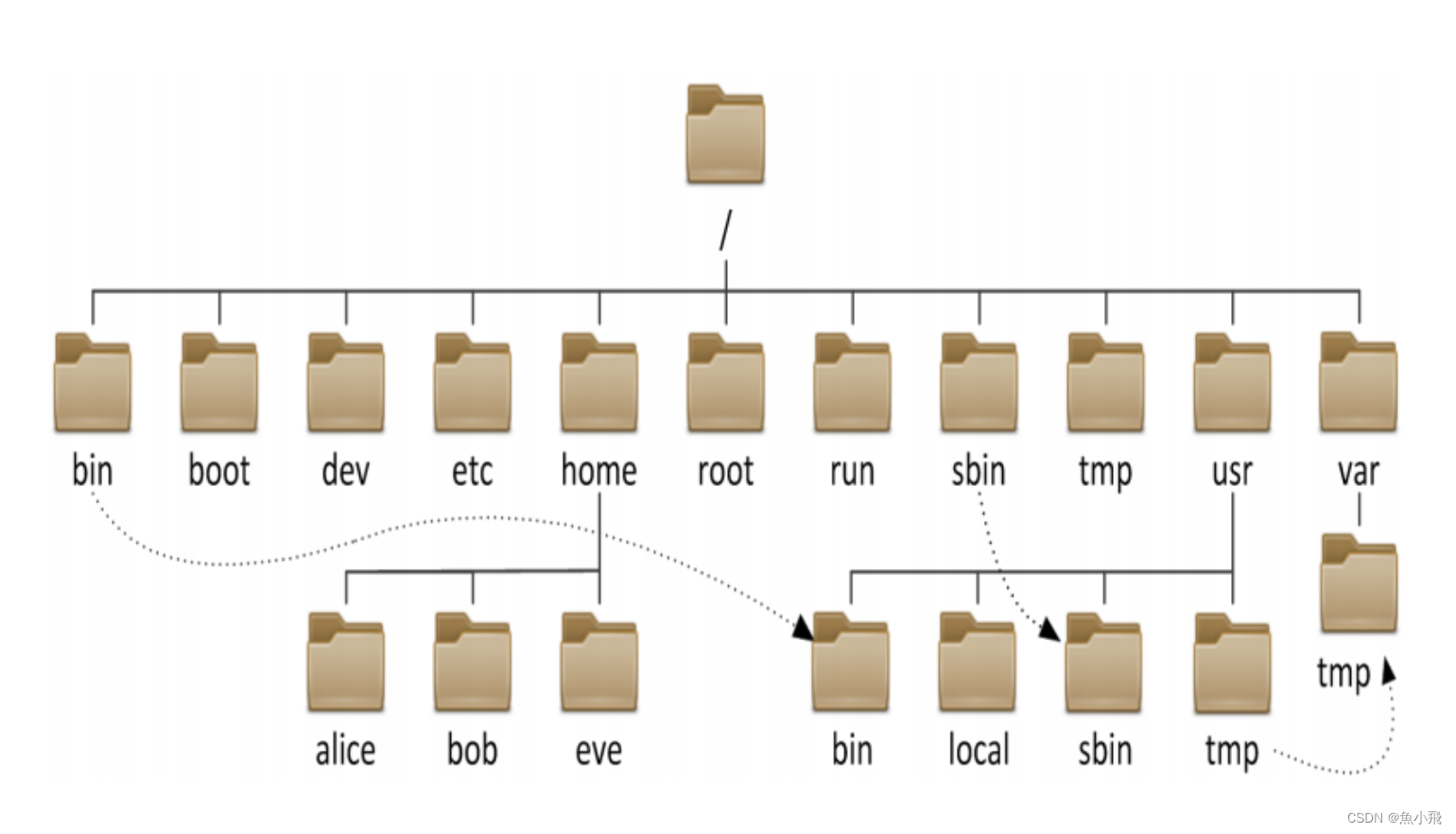
关于 IO、存储、硬盘和文件系统
关于IO、存储、硬盘和文件系统 0.引入1.了解IO1.1.存储器IO1.2.设备IO 2.存储介质和存储类型2.1.内存2.2.硬盘2.3.固态硬盘(SSD)2.4.U盘 3.硬盘的工作原理3.1.磁头3.2.盘片3.3.电动机3.4.硬盘的读写操作 4.文件系统概述4.1.文件系统的类型4.2.文件系统的…...

计算机网络期中复习提纲-酷酷的聪整理版
第一章 概述 1.请介绍计算机网络在逻辑上的组成及其各自的作用。 计算机网络在逻辑上可以分为终端子网和通信子网两部分。 终端子网是指连接计算机与网络的部分,主要负责将数据从计算机发送到通信子网,或将从通信子网接收到的数据传输到计算机。终端子网通常包括物理层和数据…...
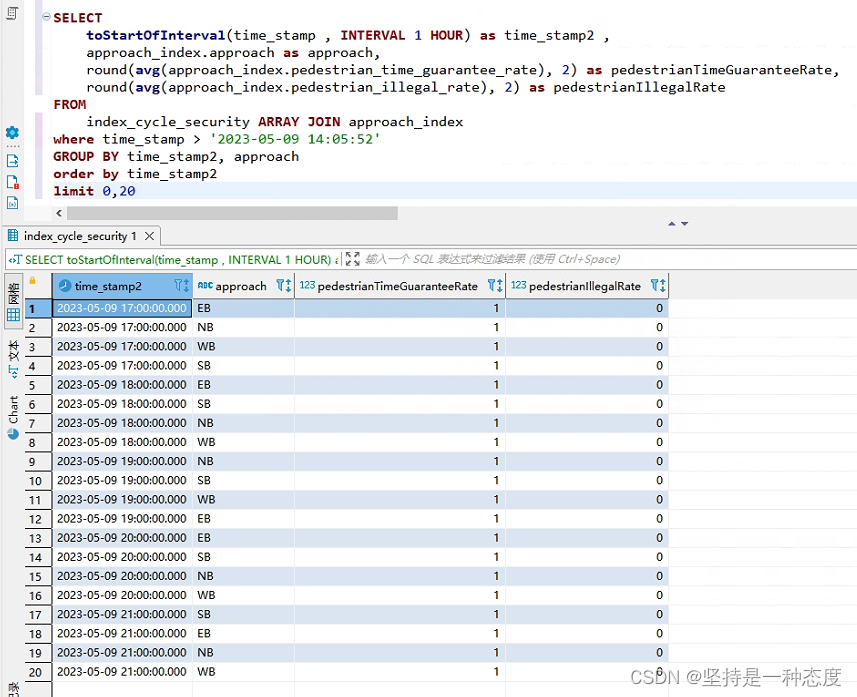
clickhouse的嵌套数据结构Tuple、Array与Nested类型介绍和使用示例
文章目录 Tuple类型Array类型Nested类型使用示例单独使用Tuple数组嵌套 Array(Tuple)Nested类型 生产使用:分组查询 Tuple类型 Tuple是ClickHouse数据库中的一种数据类型,它允许在一个字段中存储由不同数据类型组成的元组(tuple)。元组可以包含任意数量…...

人脸修复增强调研
Real-ESRGAN 工程地址:https://github.com/xinntao/Real-ESRGAN 效果: 人脸增强部分,调用的GFPGAN. GFPGAN 工程地址:https://github.com/TencentARC/GFPGAN 论文效果: BasicSR-ESRGAN: 项目地址&a…...
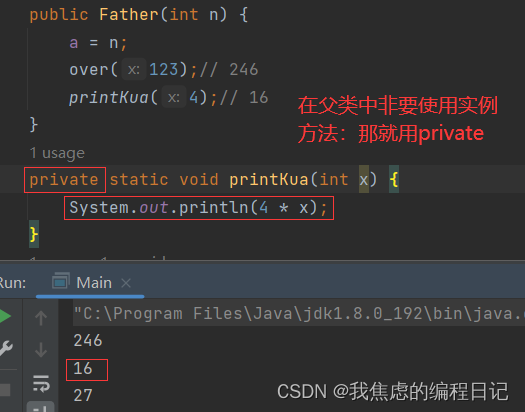
【Java】继承和多态
文章目录 一、继承1.继承的例子(is-a)2.组合的例子(has-a) 二、多态1.重写2.重载 三、继承的语法四、继承的注意事项1.初始化的顺序:2.super关键字 五、继承访问限定符六、多态实现方式七、多态的理解注意事项…...

ThingsBoard集群部署之k8s
1、概述 今天终于有时间去搞这个啦,拖了很久了,一直没时间,因为我本地没有那么多机器资源,开虚拟机不够,如果租用阿里云服务器,需要有充值的时间,因为这个费用是按小时付费,需要有连贯的时间来搞才行,今天恰好有时间,就开始搞了,弄成功搞出来了,特地写博客记录下来…...

【Gorm】如何在 GORM 中实现模型之间的关联?
文章目录 关联1、Belongs To(属于)2、Has One(拥有一个)3、Has Many(拥有多个)4、Many To Many(多对多) 关联 当涉及到 ORM(Object-Relational Mapping)的…...

Linux危险命令
rm -rf 命令 该命令可能导致不可恢复的系统崩坏。 rm -rf / #强制删除根目录下所有东西。rm -rf * #强制删除当前目录的所有文件。rm -rf . #强制删除当前文件夹及其子文件夹。fork 炸弹 :() { :|:& };:不太好理解可以转换成 bomb() {bomb|bomb& }; bomb一旦执行…...
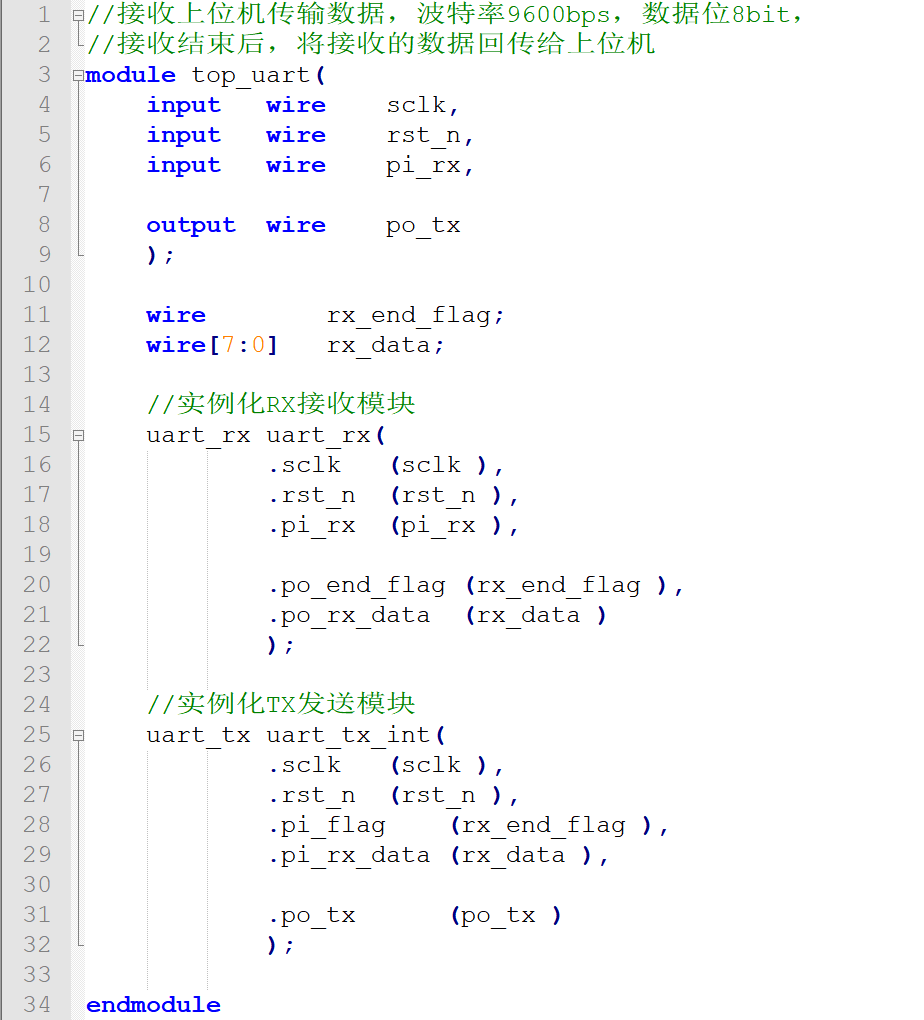
FPGA入门系列13--异步串口通信
文章简介 本系列文章主要针对FPGA初学者编写,包括FPGA的模块书写、基础语法、状态机、RAM、UART、SPI、VGA、以及功能验证等。将每一个知识点作为一个章节进行讲解,旨在更快速的提升初学者在FPGA开发方面的能力,每一个章节中都有针对性的代码…...
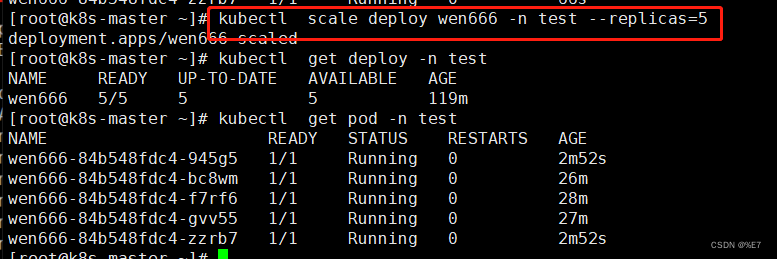
k8s基础4——deployment控制器、应用部署、升级、回滚、水平扩容缩容
文章目录 一、基本介绍二、应用程序生命周期2.1 部署应用2.2 应用升级2.2.1 修改YAML文件升级(交互式)2.2.2 命令指定镜像版本升级(免交互式)2.2.3 调用vim升级 2.3 滚动升级2.3.1 升级流程 2.4 应用回滚2.4.1 查看历史发布版本2.…...
动态规划算法——40道leetcode实例入门到熟练
目录 t0.解题五部曲1.基础入门题目1.509. 斐波那契数2.70. 爬楼梯3.746. 使用最小花费爬楼梯4.62. 不同路径5.63. 不同路径 II6.343. 整数拆分7.96. 不同的二叉搜索树 2.背包问题1.01背包(二维数组实现)2.01背包(滚动数组实现)1.4…...

Nmap入门到高级【第十一章】
预计更新第一章. Python 简介 Python 简介和历史Python 特点和优势安装 Python 第二章. 变量和数据类型 变量和标识符基本数据类型:数字、字符串、布尔值等字符串操作列表、元组和字典 第三章. 控制语句和函数 分支结构:if/else 语句循环结构&#…...
配置本地Angular环境并使用VsCode调试Angular前端项目
配置本地Angular环境并使用VsCode调试Angular前端项目 配置本地Angular环境部署Node.Js本地环境配置一下环境变量 使用vscode调试Angular安装vscode 配置本地Angular环境 部署Node.Js本地环境 1 从官网下载node.js, 本文为(v16.13.0) 下载地址: https://nodejs.org/dist/v16.…...

100ASK_全志V853-PRO开发板支持人形检测和人脸识别
1.前言 V853 芯片内置一颗 NPU核,其处理性能为最大 1 TOPS 并有 128KB 内部高速缓存用于高速数据交换,支持 OpenCL、OpenVX、android NN 与 ONNX 的 API 调用,同时也支持导入大量常用的深度学习模型。本章提供一个例程,展示如何使…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
