LeetCode——子串能表示从 1 到 N 数字的二进制串
1016. 子串能表示从 1 到 N 数字的二进制串 - 力扣(Leetcode)
目录
一、题目
二、题目解读
三、代码
一、题目
给定一个二进制字符串 s 和一个正整数 n,如果对于 [1, n] 范围内的每个整数,其二进制表示都是 s 的 子字符串 ,就返回 true,否则返回 false 。
子字符串 是字符串中连续的字符序列。
示例 1:
输入:s = "0110", n = 3 输出:true
示例 2:
输入:s = "0110", n = 4 输出:false
提示:
1 <= s.length <= 1000s[i]不是'0'就是'1'1 <= n <= 10⁹
二、题目解读
1、暴力Ⅰ
我们可以遍历1到n看是否其二级制是s的子字符串。在这个过程我们可以进行倒序进行判断,先判断较大的数。
可能有人会说这样不会超时吗?
举例说明。如果 n=7,单看闭区间 [4,7],有 4 个互不相同的整数,它们的二进制长度均为 3。如果要让字符串 s 包含这 4 个数,s 中至少要有 4 个长为 3 的互不相同的子串。考虑到这些子串可以有重叠部分,设 s 的长度为 m,则应满足 m≥3+(4−1)=6,否则直接返回false。(想象一个长为 3 的滑动窗口在 s 中滑动,至少要得到 4 个子串。)随着 n 的变大,m 的长度也应当随之变大。本题 m 至多为 1000,而 n 却高达 10⁹ 。
所有如果 n≥2014n,可以直接返回
false。Ⅱ、
反过来想,把 s 的子串都转成二进制数,如果数字在 [1,n] 内,就保存到一个哈希表中。如果哈希表的大小最终为 n,就说明 [1,n] 的二进制都在 s 里面。
2、滑动窗口
1、根据 n 和 m(字符串长度) 的值来提前判断是否要返回 false。
2、只需要考虑长为 k 和 k+1 的这两组二进制数 s 是否都有,因此可以用长为 k 和 k+1 的滑动窗口实现,从而做到线性时间复杂度。
3、进一步地,由于区间 [2ᴷ,n] 内的所有数右移一位可以得到区间 [2ᴷ⁻¹,n/2 ],所以对于 [2ᴷ⁻¹,2ᴷ−1],只需从 n/2+1 开始考虑。
三、代码
代码Ⅰ
class Solution {public boolean queryString(String s, int n) {for (int i = n; i >= 1; i--) {if (!s.contains(Integer.toBinaryString(i))) {return false;}}return true;}
}代码Ⅱ
class Solution {public boolean queryString(String S, int n) {HashSet<Integer> set = new HashSet<>();char[] s = S.toCharArray();for (int i = 0, m = s.length; i < m; ++i) {int x = s[i] - '0';if (x == 0) continue; // 二进制数从 1 开始for (int j = i + 1; x <= n; j++) {set.add(x);if (j == m) break;x = (x << 1) | (s[j] - '0'); // 子串 [i,j] 的二进制数}}return set.size() == n;}
}滑动窗口
class Solution {public boolean queryString(String s, int n) {if (n == 1)return s.contains("1");int k = 31 - Integer.numberOfLeadingZeros(n); // n 的二进制长度减一if (s.length() < Math.max(n - (1 << k) + k + 1, (1 << (k - 1)) + k - 1))return false;return check(s, k, n / 2 + 1, (1 << k) - 1) && check(s, k + 1, 1 << k, n);}// 对于长为 k 的在 [lower, upper] 内的二进制数,判断这些数 s 是否都有private boolean check(String s, int k, int lower, int upper) {if (lower > upper) return true;var seen = new HashSet<Integer>();int mask = (1 << (k - 1)) - 1;int x = Integer.parseInt(s.substring(0, k - 1), 2);for (int i = k - 1, m = s.length(); i < m; i++) {// & mask 可以去掉最高比特位,从而实现滑窗的「出」// << 1 | (s.charAt(i) - '0') 即为滑窗的「入」x = ((x & mask) << 1) | (s.charAt(i) - '0');if (lower <= x && x <= upper)seen.add(x);}return seen.size() == upper - lower + 1;}
}超详细题解可看
1016. 子串能表示从 1 到 N 数字的二进制串 - 力扣(Leetcode)
相关文章:

LeetCode——子串能表示从 1 到 N 数字的二进制串
1016. 子串能表示从 1 到 N 数字的二进制串 - 力扣(Leetcode) 目录 一、题目 二、题目解读 三、代码 一、题目 给定一个二进制字符串 s 和一个正整数 n,如果对于 [1, n] 范围内的每个整数,其二进制表示都是 s 的 子字符串 &…...
看火山引擎DataLeap如何做好电商治理(二):案例分析与解决方案
接上篇,以短视频优质项目为例,火山引擎DataLeap平台治理团队会去对每天发布的这种挂购物车车短视频打上标签,识别这些短视频它是优质的还是低质的,以及具体原因。一个视频经过这个模型识别之后,会给到奖惩中心去做相应…...

MySQL笔记-多表查询
本文标签 : 多表查询 事务四大特性 并发事务问题 事务隔离级别 文章目录 目录 文章目录 一、多表查询 1.多表关系 2.多表查询概念 3.多表查询的分类 4.内连接 5.外连接 6.自连接 7.联合查询 8.子查询 1.标量子查询 2.列子查询 3.行子查询 4.表子查询 9.多表查询案例练习 二…...
如何用100天时间,让CSDN的粉丝数从0狂飙到10000
2022年10月7日,正式开通了CSDN账号。但因为工作忙的原因,一直没有时间写博客文章,也没有投入精力在CSDN上。理所当然的,我的粉丝数量很稳定,一直保持着0的记录。 2023年春节假期过后,有点空闲时间了&#x…...

各种同质图神经网络模型的理论和节点表征学习任务的集合包rgb_experiment
诸神缄默不语-个人CSDN博文目录 最近更新时间:2023.5.10 最早更新时间:2023.5.10 本文仅考虑同质图setting下的模型。 对于异质图场景,可以参考我写的另一篇博文:异质图神经网络(持续更新ing…) node2ve…...

【C++进阶之路】类和对象(中)
文章目录 前言六大默认成员函数 一.构造函数性质默认构造函数构造函数(需要传参) 二.析构函数性质默认析构函数练习 三.拷贝构造函数基本性质:形参必须是引用默认拷贝构造浅拷贝深拷贝自定义类型 四.赋值运算符重载函数基本特征全局的运算符重载函数局部的运算符重载…...
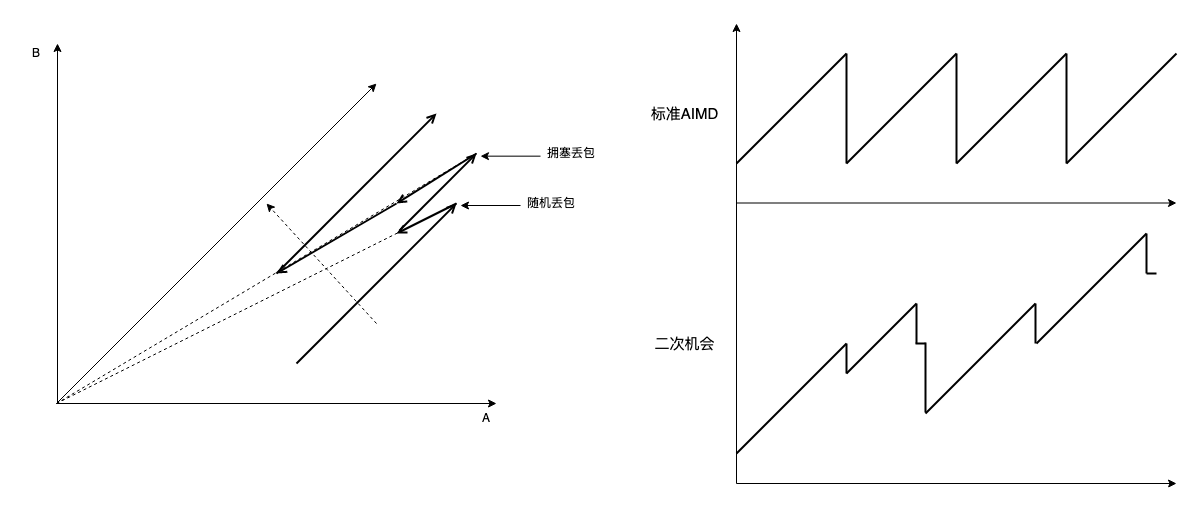
AIMD 为什么收敛(tcp reno/cubic 为什么好)
TCP 拥塞控制目标是缓解并解除网络拥塞,让所有流量公平共享带宽,合在一起就是公平收敛。 AIMD(几乎所有与拥塞控制相关的协议或算法都有 AIMD 的影子,包括 RoCE,BBRv2) 为什么收敛?我一般会给出下面的老图:…...

医院智能导诊系统,医院导航解决方案
随着现代医院规模不断扩大,功能区域越来越细化,面对复杂的楼宇结构,集中的就诊人流,患者在就诊中经常会面临找不到目的地的困境,就诊体验变差。针对这个问题,一些面积和规模都比较大的医院,已经…...
【论文复现】基于区块链的分布式光伏就地消纳交易模式研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
在滴滴和字节跳动划水4年,过于真实了...
先简单交代一下吧,沅哥是某不知名211的本硕,18年毕业加入滴滴,之后跳槽到了头条,一直从事测试开发相关的工作。之前没有实习经历,算是四年半的工作经验吧。 这四年半之间他完成了一次晋升,换了一家公司&am…...
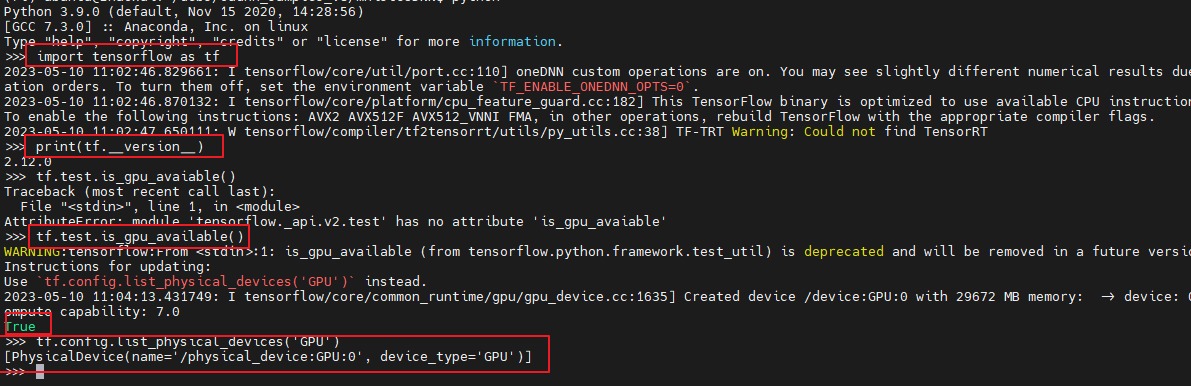
tensorflow GPU训练环境布置
tensorflow GPU训练环境布置 一、显卡驱动安装1.1 如何处理**Failed to initialize NVML: Driver/library version mismatch的问题**1.2 卸载旧的版本1.3 驱动安装 1.3.1 利用apt 安装1.3.2 手动安装 二、安装CUDA2.1 确定CUDA版本2.2 下载文件1. 找匹配版本2. 选合适的平台 2…...

理解和使用Java中的枚举
枚举是一种特殊的数据类型,用于定义一组具名的常量。Java中的枚举类型可以包含多个枚举常量,每个常量都具有唯一的名称和值。本文将详细介绍Java中的枚举,包括为什么要使用枚举、枚举的好处、如何定义和使用枚举等。 为什么要使用枚举&#…...

C++和Java:哪种语言更适合你
C和Java:哪种语言更适合你 一、引言1 背景介绍2 问题阐述3 目的和意义 二、C与Java的介绍1 C的特点和优缺点2 Java的特点和优缺点3 两种语言的比较4 选择C的理由4.1 适合底层开发的特点4.2高效的编译器和运行速度4.3 自由且灵活的语言风格4.4 良好的内存管理能力 5 …...
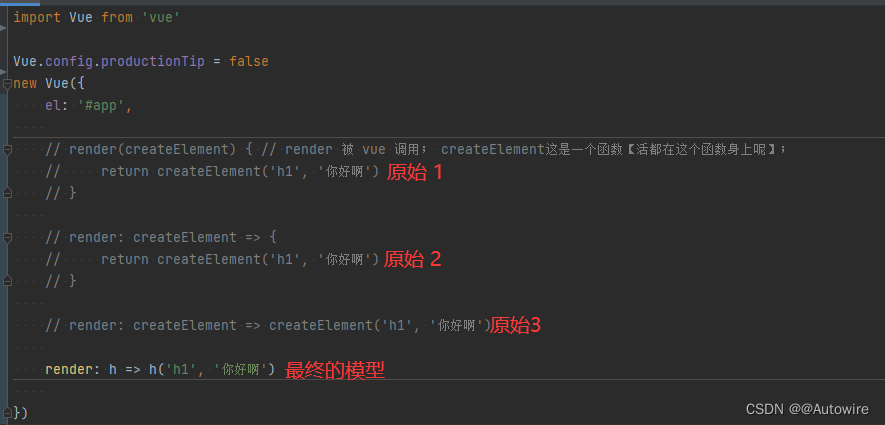
FE_Vue学习笔记 框架的执行流程详解
1 分析脚手架结构 (1)CLI就是 command line interface 的缩写。Vue CLI官网:Vue CLI (2)安装过程: (PS: 提前安装过node.js了,没有安装的可以打开这个:Downl…...

KingbaseES V8R6 等待事件之LWLock Buffer_IO
等待事件含义 当进程同时尝试访问相同页面时,等待其他进程完成其输入/输出(I/O)操作时,会发生LWLock:BufferIO等待事件。其目的是将同一页读取到共享缓冲区中。 每个共享缓冲区都有一个与LWLock:BufferIO等待事件相关联的I/O锁,每次都必须在共…...
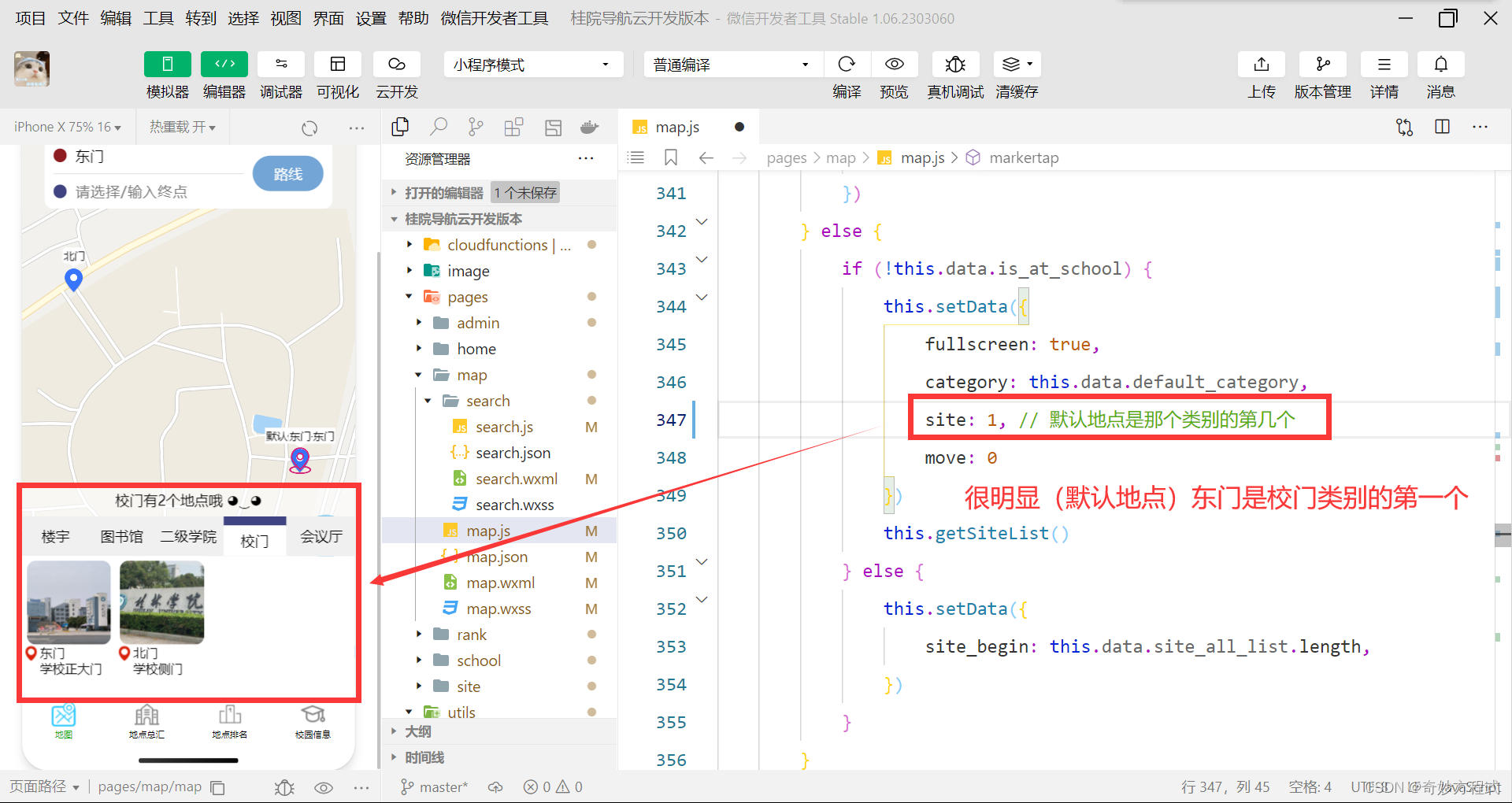
桂院导航小程序 静态项目 二次开发教程
Gitee代码仓库:桂院导航小程序 先 假装 大伙都成功安装了静态项目,并能在 微信开发者工具 和 手机 上正确运行。 接着就是 将项目 改成自己的学校。 代码里的注释我就不说明了,有提到 我的学校 的文字都改成你自己的就行 1. 全局 app.json…...

即时通讯APP开发费用成本多少?
移动互联网的发展,为人们的通讯交流提供了非常多的便利,一些即时通讯APP的出现,将人与人的距离再一次缩短。通过即时通讯APP软件,人们可以随时随地了解身边发生的新鲜事物,以及和朋友探讨各类趣事,甚至可以…...

女生学大数据好找工作么
好不好找工作和性别无关,无论你是男生还是女生,找工作的时候首先要看的都是学历,然后是个人能力,其中还有一定的面试经验和简历加分项~ 不要自己先把这个性别限定死,你有能力都能找到工作,不满足企业要求都…...
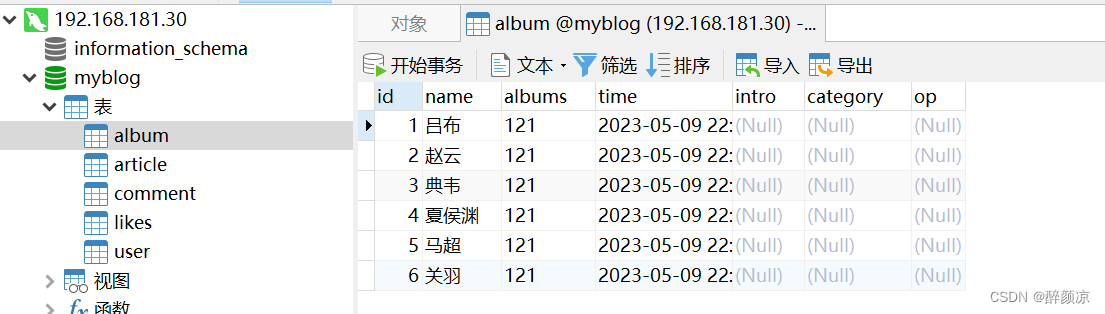
02-mysql升级篇(rpm方式+压缩包升级)
文章目录 升级方式一、二进制方式安装1、下载mysql-5.7.42安装包(mysql-5.7.37升级mysql-5.7.42)2、备份数据库、my.cnf文件,停止mysql服务(重要)3、查看当前数据库版本3、上传 mysql-5.7.42-1.el7.x86_64.rpm-bundle.…...

【Java零基础入门篇】第 ④ 期 - 继承(三)
【Java零基础入门篇】第 ④ 期 - 继承(三) 博主:命运之光专栏:Java零基础入门 学习目标 1.掌握继承性的主要作用、实现、使用限制; 2.掌握this和super的含义及其用法; 3.掌握方法覆写的操作; 4.…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
