动态规划-线性动态规划-最长上升子序列模型
title: 线性动态规划
date: 2023-05-12 08:49:10
categories:
- Algorithm
- 动态规划
tags: - 动态规划
编辑距离
题目描述
设 A A A 和 B B B 是两个字符串。我们要用最少的字符操作次数,将字符串 A A A 转换为字符串 B B B。这里所说的字符操作共有三种:
- 删除一个字符;
- 插入一个字符;
- 将一个字符改为另一个字符。
A , B A, B A,B 均只包含小写字母。
输入格式
第一行为字符串 A A A;第二行为字符串 B B B;字符串 A , B A, B A,B 的长度均小于 2000 2000 2000。
输出格式
只有一个正整数,为最少字符操作次数。
样例 #1
样例输入 #1
sfdqxbw
gfdgw
样例输出 #1
4
提示
对于 100 % 100 \% 100% 的数据, 1 ≤ ∣ A ∣ , ∣ B ∣ ≤ 2000 1 \le |A|, |B| \le 2000 1≤∣A∣,∣B∣≤2000。
思路
状态表示:f[i][j]表示将A的1~i变成B的1~j的操作次数的最小值
状态计算:三种操作方式如下:
-
删除:将
A[i]删除后应该与B[1~j]相同,说明A[1~(i-1)]==B[1~j] -
- 方程为:
f[i-1][j]+1
- 方程为:
-
插入:在
A[i]之后插入后与B[1~j]相同,则说明A[1~i]==B[1~j-1] -
- 方程为:
f[i][j-1]+1
- 方程为:
-
替换:将
A[i]替换后,A[1~i]==B[1~j]分两种情况: -
- 第一种是
A[i]==B[j]已经相等了不需要替换,f[i-1][j-1] - 第二种是不想等,需要替换一次,
f[i-1][j-1]+1
- 第一种是
状态转移方程为上述三个取min
初始化的时候需要将:
f[i][0]=i表示删除i个字符与B相等f[0][i]=i表示添加i个字符与B相等
或者这样考虑:
f[i][j]表示将A的1~i变成B的1~j的操作次数的最小值
如果
A[i]==B[j],则f[i][j]=f[i-1][j-1],如果
A[i]!=B[j], 使用三种操作,取最小值
- 修改:将
a[i]改为b[i],f[i-1][j-1]+1- 插入:在
a[i]后面插入b[i],f[i][j-1]+1- 删除:将
a[i]删除,f[i-1][j]+1
代码
#include <bits/stdc++.h>#define int long long
using namespace std;
const int N = 2010;
int f[N][N];//将A 1-i变成 B 1-j的最小操作次数
string a, b;signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifcin >> a >> b;int n = a.size(), m = b.size();a = " " + a, b = " " + b;for (int i = 1; i <= n; i++) f[i][0] = i;for (int i = 1; i <= m; i++) f[0][i] = i;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (a[i] == b[j]) f[i][j] = f[i - 1][j - 1];else f[i][j]= min(f[i-1][j-1], min(f[i-1][j],f[i][j-1]))+1;}}cout << f[n][m];return 0;
}
899. 编辑距离 - AcWing
给定 n n n 个长度不超过 10 10 10 10 10 10 的字符串以及 m m m次询问,每次询问给出一个字符串和一个操作次数上限。
对于每次询问,请你求出给定的 n n n 个字符串中有多少个字符串可以在上限操作次数内经过操作变成询问给出的字符串。
每个对字符串进行的单个字符的插入、删除或替换算作一次操作。
输入格式
第一行包含两个整数 n n n 和 m m m。
接下来 n n n 行,每行包含一个字符串,表示给定的字符串。
再接下来 m m m 行,每行包含一个字符串和一个整数,表示一次询问。
字符串中只包含小写字母,且长度均不超过 10 10 10 10 10 10。
输出格式
输出共 m m m 行,每行输出一个整数作为结果,表示一次询问中满足条件的字符串个数。
数据范围
1 ≤ n , m ≤ 1000 1 \le n, m \le 1000 1≤n,m≤1000 1 ≤ n , m ≤ 1000 1 \le n, m \le 1000 1≤n,m≤1000,
输入样例:
3 2
abc
acd
bcd
ab 1
acbd 2
输出样例:
1
3
思路
和上一题一样,将dp封装为一个函数即可。暴力统计是否能够转换。
代码
#include <bits/stdc++.h>#define int long long
using namespace std;
const int N = 20;
int f[N][N];int edit(string a, string b) {int n = a.size(), m = b.size();a = " " + a, b = " " + b;for (int i = 1; i <= n; i++) f[i][0] = i;for (int i = 1; i <= m; i++) f[0][i] = i;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (a[i] == b[j]) f[i][j] = f[i - 1][j - 1];else f[i][j] = min(f[i - 1][j - 1], min(f[i][j - 1], f[i - 1][j])) + 1;}}return f[n][m];
}signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifint n, m;cin >> n >> m;vector<string> a(n + 1);for (int i = 1; i <= n; i++) cin >> a[i];while (m--) {string s;int limit;cin >> s >> limit;int res = 0;for (int i = 1; i <= n; i++) {if (edit(a[i], s) <= limit) res++;}cout << res << endl;}return 0;
}
[NOIP1999 普及组] 导弹拦截
题目描述
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度,计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
输入格式
一行,若干个整数,中间由空格隔开。
输出格式
两行,每行一个整数,第一个数字表示这套系统最多能拦截多少导弹,第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
样例 #1
样例输入 #1
389 207 155 300 299 170 158 65
样例输出 #1
6
2
提示
对于前 50 % 50\% 50% 数据(NOIP 原题数据),满足导弹的个数不超过 1 0 4 10^4 104 个。该部分数据总分共 100 100 100 分。可使用 O ( n 2 ) \mathcal O(n^2) O(n2) 做法通过。
对于后 50 % 50\% 50% 的数据,满足导弹的个数不超过 1 0 5 10^5 105 个。该部分数据总分也为 100 100 100 分。请使用 O ( n log n ) \mathcal O(n\log n) O(nlogn) 做法通过。
对于全部数据,满足导弹的高度为正整数,且不超过 5 × 1 0 4 5\times 10^4 5×104。
思路 (LIS+贪心 O ( n 2 ) O(n^2) O(n2))
第一问是LIS问题:
LIS 是 Longest ascending subsequence 的缩写
显然每套导弹拦截系统拦截导弹高度为步上升子序列,也就是最长不上升子序列,只需要求最长不上升子序列的长度就可以了,
状态的计算:
for (int j = 0; j < i; j++) if (q[j] >= q[i]) { // 不高于, 可以等于, 最长下降子序列(不完全下降,可以等于),严格来说是不上升子序列f[i] = max(f[i], f[j] + 1);
第二问是贪心问题:
贪心思路:
- 较大的数的末尾元素比较小的数作为末尾元素的子序列更好,因为这样可以让这个子序列变得更长,如果放了一个较小的数,可能放的数就没有那么长了
贪心步骤:
-
开一个数组
q[]记录所有下降子序列末尾元素 -
遍历每一个数,对于当前的这个数:
-
q[]中所有的数都比这个数大,那么我们就扩大q[]的长度,并且把这个数放到q[]中刚开的地方q[]中存在比这个数小的数,那么我们就把当前的这个数覆盖到找到的比这个数小的最大的数
-
每次将一个较小的数换成一个较大的数作为末尾元素存储到
q[], 随着q[]的长度扩大, 也就表示此时新增x比所有末尾元素都大时;q[]随下标增大元素值也越大, 因此q[]是单调上升的数组
这题的思路和AcWing 896. 最长上升子序列 II 一样,我们可以得出结论:
求解至少需要多少个下降子序列的数目 和
求解至多含有多少个上升子序列的数目是一个对偶问题
注:数组q[]是单调不减的!!!
代码
#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;
int n;
int q[N];
int f[N], g[N];int main() {while (cin >> q[n]) n++;int res = 0;for (int i = 0; i < n; ++i) {f[i] = 1;for (int j = 0; j < i; j++) {if (q[j] >= q[i]) { // 不高于, 可以等于, 最长下降子序列f[i] = max(f[i], f[j] + 1);}}res = max(res, f[i]);}cout << res << endl;int cnt = 0;//当前子序列的个数for (int i = 0; i < n; i++) {int k = 0;//记录下从前往后找到的比当前的数q[i]小的最大的数while (k < cnt && g[k] < q[i]) k++;// 当前的序列结尾的数<=我们的数g[k] = q[i];if (k >= cnt) cnt++;//没有任何一个数是大于等于我们当前数的}cout << cnt << endl;return 0;
}思路2( O ( n 2 ) O(n^2) O(n2))
可以把题目理解为:
- 给定一个序列,求至少包含多少个下降子序列数目
等价于
- 给定一个序列,求至多包含多少个上升子序列数目
也就是将题目转换为求解最长上升子序列的长度。
代码
#include <iostream>
#include <algorithm>
using namespace std;const int N = 1010;
int n;
int a[N], f[N];int main()
{// 第一问:问题是求最长下降子序列的长度while(cin >> a[n])n++;int res = 0;for (int i = 0; i < n; ++i) {f[i] = 1;for (int j = 0; j < i; ++j)if (a[i] <= a[j])f[i] = max(f[i], f[j] + 1);res = max(res, f[i]);}// 第二问:问题转化为求解最长上升子序列的长度int len = 0;for (int i = 0; i < n; ++i) {f[i] = 1;for (int j = 0; j < i; ++j) if (a[i] > a[j])f[i] = max(f[i], f[j] + 1);len = max(len, f[i]);}cout << res << endl;cout << len << endl;return 0;
}
思路3(二分+LIS O ( n l o g n ) O(nlogn) O(nlogn))
注意这里第一问需要倒着求最长上升子序列,这里的上升可以相等,因此使用的是upper_bound函数
代码
#include <bits/stdc++.h>#define int long long
using namespace std;const int N = 1e5 + 10;
int a[N];
int n = 1;signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifwhile (cin >> a[n])n++;n--;vector<int> f;f.push_back(a[n]);for (int i = n - 1; i >= 1; i--) {if (a[i] >= f.back()) f.push_back(a[i]);else {//找到第一个大于a[i]的数,换成a[i]*std::upper_bound(f.begin(), f.end(), a[i]) = a[i];}}cout << f.size() << endl;vector<int> g;g.push_back(a[1]);for (int i = 2; i <= n; i++) {if (a[i] > g.back())g.push_back(a[i]);else *std::lower_bound(g.begin(), g.end(), a[i]) = a[i];}cout << g.size() << endl;return 0;
}
187. 导弹防御系统
题目链接:https://www.acwing.com/problem/content/189/
为了对抗附近恶意国家的威胁, R R R 国更新了他们的导弹防御系统。
一套防御系统的导弹拦截高度要么一直 严格单调 上升要么一直 严格单调 下降。
例如,一套系统先后拦截了高度为 3 3 3 和高度为 4 4 4的两发导弹,那么接下来该系统就只能拦截高度大于 4 4 4 的导弹。
给定即将袭来的一系列导弹的高度,请你求出至少需要多少套防御系统,就可以将它们全部击落。
输入格式
输入包含多组测试用例。
对于每个测试用例,第一行包含整数 n n n,表示来袭导弹数量。
第二行包含 n n n 个不同的整数,表示每个导弹的高度。
当输入测试用例 n = 0 n=0 n=0 时,表示输入终止,且该用例无需处理。
输出格式
对于每个测试用例,输出一个占据一行的整数,表示所需的防御系统数量。
数据范围
1 ≤ n ≤ 50 1 \le n \le 50 1≤n≤50
输入样例:
5
3 5 2 4 1
0
输出样例:
2
样例解释
对于给出样例,最少需要两套防御系统。
一套击落高度为 3 , 4 3,4 3,4 的导弹,另一套击落高度为 5 , 2 , 1 5,2,1 5,2,1 的导弹。
思路(DFS,迭代加深,剪枝,贪心)
用up[k]和down[k]记录第k套上升(下降)系统目前所拦截的最后一个导弹
dfs(u,v,t)意味着已有u个上升,v个下降,正在处理第t个数
代码
#include <bits/stdc++.h>#define int long long
using namespace std;int n;
const int N = 60;
int a[N];
int up[N], down[N];
int ans = 0;/*** @param u 当前第几个导弹* @param s 上* @param x 下*/
void dfs(int u, int s, int x) {if (s + x >= ans) return;if (u >= n + 1) {ans = s + x;return;}//将当前数放到上升子序列中int k = 0;while (k < s && up[k] >= a[u]) k++; //大于等于当前数int t = up[k];up[k] = a[u];if (k < s) dfs(u + 1, s, x);else dfs(u + 1, s + 1, x);up[k] = t;//回溯//将当前数放到下降子序列中k = 0;while (k < x && down[k] <= a[u]) k++;//小于等于当前数t = down[k];down[k] = a[u];if (k < x) dfs(u + 1, s, x);else dfs(u + 1, s, x + 1);down[k] = t;
}void solve() {for (int i = 1; i <= n; i++) cin >> a[i];ans = n;dfs(1, 0, 0);cout << ans << endl;
}signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifwhile (cin >> n, n) {solve();}return 0;
}
AcWing 272. 最长公共上升子序列
题目链接:https://www.acwing.com/problem/content/274/
熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。
小沐沐先让奶牛研究了最长上升子序列,再让他们研究了最长公共子序列,现在又让他们研究最长公共上升子序列了。
小沐沐说,对于两个数列 A 和 B ,如果它们都包含一段位置不一定连续的数,且数值是严格递增的,那么称这一段数是两个数列的公共上升子序列,而所有的公共上升子序列中最长的就是最长公共上升子序列了。
奶牛半懂不懂,小沐沐要你来告诉奶牛什么是最长公共上升子序列。
不过,只要告诉奶牛它的长度就可以了。
数列 A 和 B 的长度均不超过 3000 。
输入格式
第一行包含一个整数 N N N,表示数列 A , B A,B A,B 的长度。
第二行包含 N N N 个整数,表示数列 A A A。
第三行包含 N N N 个整数,表示数列 B B B。
输出格式
输出一个整数,表示最长公共上升子序列的长度。
数据范围
1 ≤ N ≤ 3000 1 \le N \le 3000 1≤N≤3000,序列中的数字均不超过 2 31 − 1 2^{31}-1 231−1。
输入样例:
4
2 2 1 3
2 1 2 3
输出样例:
2
思路
动态规划:
-
状态表示:
f[i][j]代表所有a[1 ~ i]和b[1 ~ j]中以b[j]结尾的公共上升子序列的集合的子序列长度的最大值。 -
状态计算:首先依据公共子序列中是否包含
a[i],将f[i][j]所代表的集合划分成两个不重不漏的子集: -
- 不包含
a[i]的子集,最大值是f[i - 1][j]; - 包含
a[i]的子集,将这个子集继续划分,依据是子序列的倒数第二个元素在b[]中是哪个数:
- 不包含
-
-
- 子序列只包含
b[j]一个数,长度是1; - 子序列的倒数第二个数是
b[1]的集合,最大长度是f[i - 1][1] + 1; - …
- 子序列的倒数第二个数是
b[j - 1]的集合,最大长度是f[i - 1][j - 1] + 1;
- 子序列只包含
-
代码
#include <bits/stdc++.h>#define int long long
using namespace std;const int N = 3010;
int f[N][N];
int a[N], b[N];
int n;signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifcin >> n;for (int i = 1; i <= n; i++) cin >> a[i];for (int i = 1; i <= n; i++) cin >> b[i];for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (a[i] != b[j]) f[i][j] = f[i - 1][j];else {int mx = 0;for (int k = 1; k < j; k++) {if (b[k] < b[j]) mx = max(mx, f[i - 1][k]);}f[i][j] = mx + 1;}}}int res = 0;for (int i = 1; i <= n; i++) res = max(res, f[n][i]);cout << res << endl;return 0;
}
优化:使用define int long long 会内存超限
开一个变量maxn记录下子序列的倒数第二个元素在b[]中是哪个数的最大值,防止每次都去求一次最大值。
代码
#include <bits/stdc++.h>using namespace std;const int N = 3010;
int f[N][N];
int a[N], b[N];
int n;int main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifcin >> n;for (int i = 1; i <= n; i++) cin >> a[i];for (int i = 1; i <= n; i++) cin >> b[i];for (int i = 1; i <= n; i++) {int mx = 0;for (int j = 1; j <= n; j++) {if (a[i] != b[j]) f[i][j] = f[i - 1][j];else f[i][j] = max(f[i][j], mx + 1);if (a[i] > b[j]) mx = max(mx, f[i - 1][j] );}}int res = 0;for (int i = 1; i <= n; i++) res = max(res, f[n][i]);cout << res << endl;return 0;
}
相关文章:

动态规划-线性动态规划-最长上升子序列模型
title: 线性动态规划 date: 2023-05-12 08:49:10 categories: Algorithm动态规划 tags:动态规划 编辑距离 题目描述 设 A A A 和 B B B 是两个字符串。我们要用最少的字符操作次数,将字符串 A A A 转换为字符串 B B B。这里所说的字符操作共有三种࿱…...
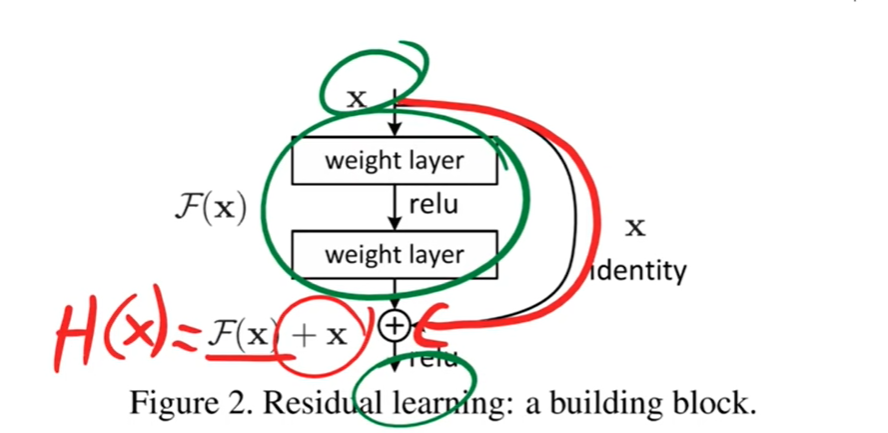
ResNet 论文理解含视频
ResNet 论文理解 论文理解 ResNet 网络的论文名字是《Deep Residual Learning for Image Recognition》,发表在2016年的 CVPR 上,获得了 最佳论文奖。ResNet 中的 Res 也是 Residual 的缩写,它的用意在于基于 残差 学习,让神经网…...

Java8之Stream操作
Java8之Stream操作 stream干啥用的?创建流中间操作终结操作好文推荐----接口优化思想 stream干啥用的? Stream 就是操作数据用的。使用起来很方便 创建流 → 中间操作 → 终结操作 Stream的操作可以分为两大类:中间操作、终结操作 中间操作可…...
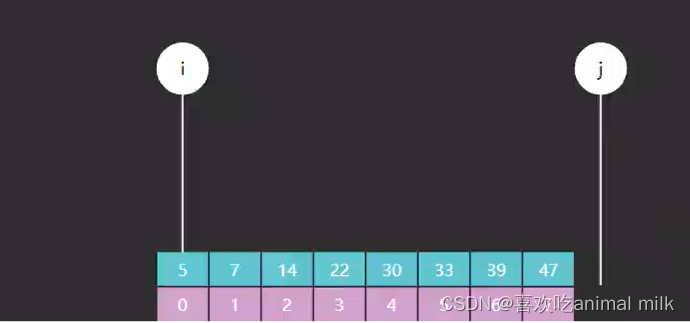
二分查找基础篇-JAVA
文章目录 前言 大家好,我是最爱吃兽奶,这篇博客给大家介绍一下二分查找,我们先从最基本的开始讲解,再慢慢深入,把优化和变形也和大家说一下,那么,跟着我的步伐,我们一起去看看吧! 一、什么是二分查找? 二分查找(Binary Search)也称作折半查找 二分查找的效率很高,每查找一次…...
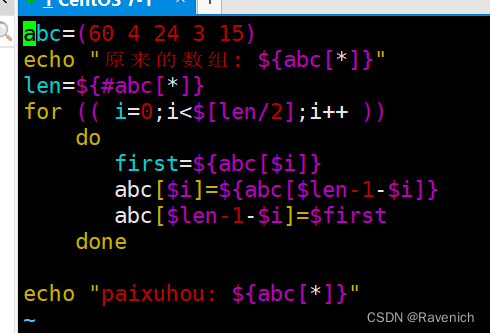
shell脚本5数组
文章目录 数组1 数组定义方法2 获取数组长度2.1 读取数组值2.2 数组切片2.3 数组替换2.4 数组删除2.5 追加数组元素 3 实验3.1 冒泡法3.2 直接选择法3.3 反排序法 数组 1 数组定义方法 数组名(value0 valuel value2 …) 数组名( [0]value [1]value [2]value …) 列表名“val…...
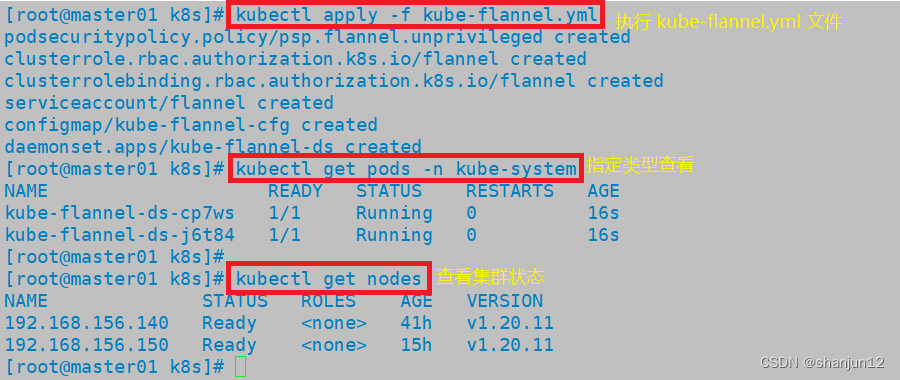
Kubernetes二进制部署 单节点
目录 1.环境准备 1.关闭防火墙和selinux 2.关闭swap 3.设置主机名 4.在master添加hosts 5.桥接的IPv4流量传递到iptables的链 6.时间同步 2.部署etcd集群 1.master节点部署 2.在node1与node2节点修改 3.在master1节点上进行启动 4.部署docker引擎 3.部署 Master 组…...
基于VC + MSSQL实现的县级医院医学影像PACS
一、概述: 基于VC MSSQL实现的一套三甲医院医学影像PACS源码,集成3D后处理功能,包括三维多平面重建、三维容积重建、三维表面重建、三维虚拟内窥镜、最大/小密度投影、心脏动脉钙化分析等功能。 二、医学影像PACS实现功能: 1、…...

Jmeter 压测 QPS
文章目录 1、准备工作1.1 Jmeter的基本概念1.2 Jmeter的作用1.3.Windows下Jmeter下载安装1.4 Jmeter的目录结构1.5 启动1.6 设置中文1.6.1 设置调整1.6.2 配置文件调整(一劳永逸) 2、Jmeter线程组基本操作2.1 线程组是什么2.2 线程组2.2.1 创建线程组2.2…...
如何在云上部署java项目
最近博主接了一波私活,由于上云的概念已经深入人心,客户要求博主也上云,本文将介绍上云的教程。 1.如何选择服务器 这里博主推荐阿里云服务器,阿里云云服务器ECS是一种安全可靠、弹性可伸缩的云计算服务,助您降低 IT…...
IT行业项目管理软件,你知道多少?
IT行业项目管理软件,主要得看用来管理的是软件研发还是做IT运维。如果是做软件研发,那还得看项目经理是用什么思路,是传统的瀑布式方法还是敏捷的方法或者是混合的方法。 如果用来管理的是IT运维工作,那么很多通用型的项目管理软件…...

小爱同学接入chatGPT
大致流程 最近入手了一款小爱音响,想着把小爱音响接入 chatGPT, 在 github 上找了一个非常优秀的开源项目,整个过程还是比较简单的,一次就完成了。 其中最难的技术点是 如何获取与小爱的对话记录?如何让小爱播放文本?…...

java运算符
1.运算符和表达式 运算符: 就是对常量或者变量进行操作的符号。 比如: - * / 表达式: 用运算符把常量或者变量连接起来的,符合Java语法的式子就是表达式。 比如:a b 这个整体就是表达式。 而其…...

StrongSORT_文献翻译
StrongSORT 【摘要】 现有的MOT方法可以被分为tracking-by-detection和joint-detection-association。后者引起了更多的关注,但对于跟踪精度而言,前者仍是最优的解决方案。StrongSORT在DeepSORT的基础之上,更新了它的检测、嵌入和关联等多个…...

Python每日一练(20230512) 跳跃游戏 V\VI\VII
目录 1. 跳跃游戏 V 2. 跳跃游戏 VI 3. 跳跃游戏 VII 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏 1. 跳跃游戏 V 给你一个整数数组 arr 和一个整数 d 。每一步你可以从下标 i 跳到&a…...

k8s部署mysql并使用nfs持久化数据
k8s部署mysql并使用nfs持久化数据 一、配置nfs服务器1.1 修改配置文件1.2. 载入配置1.3. 检查服务配置 二、创建K8S资源文件2.1 mysql-deployment.yml2.2 mysql-svc.yml 一、配置nfs服务器 参考文章: pod使用示例https://cloud.tencent.com/developer/article/1914388nfs配置…...

AI时代的赚钱思路:23岁女网红如何利用AI技术年入4亿?
一、AI技术为网红赚钱创造新途径 23岁美国网红Caryn Marjorie(卡琳玛乔丽)正同时交往1000多个男朋友。 作为一个在Snapchat上坐拥180万粉丝的美女,她利用人工智能(AI)技术,打造了一个AI版本的自己&#x…...

如何修复d3dcompiler_47.dll缺失?多种解决方法分享
在使用Windows操作系统的过程中,有时候会遇到d3dcompiler_47.dll缺失的情况。这个问题可能会导致某些应用程序无法正常运行,因此需要及时解决。本文将介绍如何修复d3dcompiler_47.dll缺失的问题。 一.什么是d3dcompiler_47.dll D3dcompiler_47.dll是Di…...

【项目实训】ATM自助取款系统
文章目录 1. 课程设计目的2. 课程设计任务与要求3. 课程设计说明书3.1 需求分析3.1.1 功能分析3.1.2 性能要求分析 3.2 概要设计3.2.1 功能模块图 3.3 详细设计3.3.1 实体类的设计3.3.2 实现数据库处理 3.4 主要程序功能流程图 4. 课程设计成果4.1 完整代码4.2 运行结果4.2.1 精…...
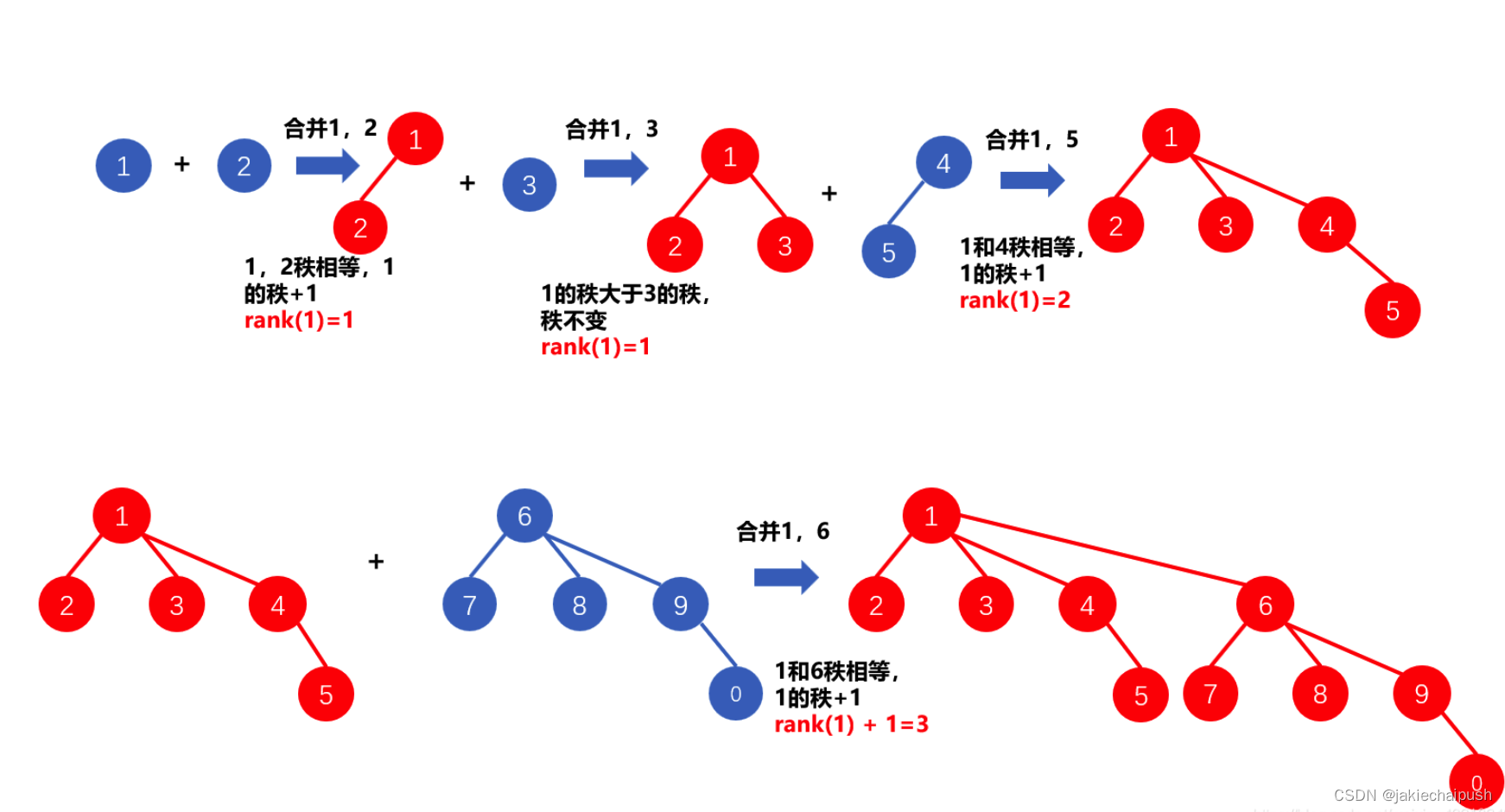
并查集算法
文章目录 1. 原理介绍2. 并查集的应用3. find()函数的定义与实现4. 并查集的join函数5. 路径压缩优化算法-优化find6. 路径压缩优化算法按秩合并算法 1. 原理介绍 并查集是一种用于维护集合关系的数据结构,它支持合并集合和查询元素所在的集合。它的基本思想是将元…...
十分钟在 macOS 快速搭建 Linux C/C++ 开发环境
有一个使用了 Epoll 的 C 项目,笔者平时用的 Linux 主力开发机不在身边,想在 macOS 上开发调试,但是没有 Linux 虚拟机。恰好,JetBrains CLion 的 Toolchains 配置除了使用本地环境,还支持 SSH、Docker。 笔者使用 CL…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
