《统计学习方法》——隐马尔可夫模型(下)
学习算法
HMM的学习,在有观测序列的情况下,根据训练数据是否包含状态序列,可以分别由监督学习算法和无监督学习算法实现。
监督学习算法
监督学习算法就比较简单,基于已有的数据利用极大似然估计法来估计隐马尔可夫模型的参数。分为以下几步:
1.转移概率 a i j a_{ij} aij的估计
设样本中时刻 t t t处于状态 i i i,时刻 t + 1 t+1 t+1转到到状态 j j j的频数为 A i j A_{ij} Aij,那么状态转移概率 a i j a_{ij} aij的估计是
a ^ i j = A i j ∑ j N A i j , i = 1 , 2 , ⋯ , N ; j = 1 , 2 , ⋯ , N (10.30) \hat a_{ij} = \frac{A_{ij}}{\sum_j^N A_{ij}},\quad i=1,2,\cdots,N; \quad j=1,2,\cdots,N \tag{10.30} a^ij=∑jNAijAij,i=1,2,⋯,N;j=1,2,⋯,N(10.30)
2.观测概率 b j ( k ) b_j(k) bj(k)的估计
设样本中状态为 j j j并观测为 k k k的频数是 B j k B_{jk} Bjk,那么状态为 j j j观测为 k k k的概率 b j ( k ) b_j(k) bj(k)的估计是
b ^ j ( k ) = B j k ∑ k = 1 M B j k , j = 1 , 2 , ⋯ , N ; k = 1 , 2 , ⋯ , M (10.31) \hat b_j(k) = \frac{B_{jk}}{\sum_{k=1}^M B_{jk}}, \quad j=1,2,\cdots,N; \quad k=1,2,\cdots, M \tag{10.31} b^j(k)=∑k=1MBjkBjk,j=1,2,⋯,N;k=1,2,⋯,M(10.31)
3.初始状态概率 π i \pi_i πi的估计 π ^ i \hat \pi_i π^i为 S S S个样本中初始状态为 q i q_i qi的频率
一般没有这么多标注的训练数据,因此通常采用的是无监督学习方法,下面介绍一种。
Baum-Welch算法
假设给定训练数据只包含 S S S个长度为 T T T的观测序列 { O 1 , ⋯ , O S } \{O_1,\cdots,O_S\} {O1,⋯,OS}而没有对应的状态序列,目标是学习隐马尔可夫模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)的参数。我们将观测序列数据看作观测数据 O O O,状态序列数据看作不可观测的隐数据 I I I,那么隐马尔可夫模型事实上是一个含有隐变量的概率模型
P ( O ∣ λ ) = ∑ I P ( O , I ∣ λ ) = ∑ I P ( O ∣ I , λ ) P ( I ∣ λ ) (10.32) P(O|\lambda) =\sum_I P(O,I|\lambda) = \sum_I P(O|I,\lambda) P(I|\lambda) \tag{10.32} P(O∣λ)=I∑P(O,I∣λ)=I∑P(O∣I,λ)P(I∣λ)(10.32)
它的参数学习可以由EM算法实现。
1.确定完全数据的对数似然函数
所有观测数据写成 O = ( o 1 , ⋯ , o T ) O=(o_1,\cdots,o_T) O=(o1,⋯,oT),所有隐数据写成 I = ( i 1 , ⋯ , i T ) I=(i_1,\cdots,i_T) I=(i1,⋯,iT),完全数据是 ( O , I ) = ( o 1 , o 2 , ⋯ , o T , i 1 , i 2 , ⋯ , i T ) (O,I)=(o_1,o_2,\cdots,o_T,i_1,i_2,\cdots,i_T) (O,I)=(o1,o2,⋯,oT,i1,i2,⋯,iT)。完全数据的对数似然函数是 log P ( O , I ∣ λ ) \log P(O,I|\lambda) logP(O,I∣λ)。
2.EM算法的E步:求 Q Q Q函数 Q ( λ , λ ˉ ) Q(\lambda,\bar \lambda) Q(λ,λˉ)
按照 Q Q Q函数的定义,
Q ( λ , λ ˉ ) = E I [ log P ( O , I ∣ λ ) ∣ O , λ ˉ ] = ∑ I log P ( O , I ∣ λ ) P ( I ∣ O , λ ˉ ) = ∑ I log P ( O , I ∣ λ ) P ( O , I ∣ λ ˉ ) P ( O ∣ λ ˉ ) = 1 P ( O ∣ λ ˉ ) ∑ I log P ( O , I ∣ λ ) P ( O , I ∣ λ ˉ ) 与 I 无 关 可 以 提 出 去 \begin{aligned} Q(\lambda,\bar \lambda) &= E_I[\log P(O,I|\lambda)|O,\bar \lambda] \\ &= \sum_I \log P(O,I|\lambda)P(I|O,\bar \lambda) \\ &= \sum_I \log P(O,I|\lambda)\frac{P(O,I|\bar \lambda)}{P(O|\bar \lambda)} \\ &= \frac{1}{P(O|\bar \lambda)}\sum_I \log P(O,I|\lambda)P(O,I|\bar \lambda) & 与I无关可以提出去\\ \end{aligned} Q(λ,λˉ)=EI[logP(O,I∣λ)∣O,λˉ]=I∑logP(O,I∣λ)P(I∣O,λˉ)=I∑logP(O,I∣λ)P(O∣λˉ)P(O,I∣λˉ)=P(O∣λˉ)1I∑logP(O,I∣λ)P(O,I∣λˉ)与I无关可以提出去
其中 λ ˉ \bar \lambda λˉ是隐马尔可夫模型参数的当前估计值, λ \lambda λ是要极大化的隐马尔可夫模型参数。
λ ˉ \bar \lambda λˉ是一个常量,上式中 P ( O ∣ λ ˉ ) P(O|\bar \lambda) P(O∣λˉ)对于 λ \lambda λ而言是一个常数项,省去该项就得到了:
Q ( λ , λ ˉ ) = ∑ I log P ( O , I ∣ λ ) P ( O , I ∣ λ ˉ ) (10.33) Q(\lambda,\bar \lambda) =\sum_I \log P(O,I|\lambda)P(O,I|\bar \lambda) \tag{10.33} Q(λ,λˉ)=I∑logP(O,I∣λ)P(O,I∣λˉ)(10.33)
而根据式 ( 10.12 ) (10.12) (10.12):
P ( O , I ∣ λ ) = π i 1 b i 1 ( o 1 ) a i 1 , i 2 b i 2 ( o 2 ) ⋯ a i T − 1 , i T b i T ( o T ) P(O,I|\lambda) = \pi_{i_1} b_{i_1}(o_1)a_{i_1,i_2}b_{i_2}(o_2)\cdots a_{i_{T-1},i_T}b_{i_T}(o_T) P(O,I∣λ)=πi1bi1(o1)ai1,i2bi2(o2)⋯aiT−1,iTbiT(oT)
我们要求的就是 π , A , B \pi,A,B π,A,B,因此对上式按这三个参数分开。
于是函数 Q ( λ , λ ˉ ) Q(\lambda, \bar \lambda) Q(λ,λˉ)可以写成:
Q ( λ , λ ˉ ) = ∑ I log P ( O , I ∣ λ ) P ( O , I ∣ λ ˉ ) = ∑ I log [ π i 1 b i 1 ( o 1 ) a i 1 , i 2 b i 2 ( o 2 ) ⋯ a i T − 1 , i T b i T ( o T ) ] P ( O , I ∣ λ ˉ ) = ∑ I [ log ( π i 1 ) + log ( a i 1 , i 2 a i 2 , i 3 a i T − 1 , i T ) + log ( b i 1 ( o 1 ) b i 2 ( o 2 ) ⋯ b i T ( o T ) ] P ( O , I ∣ λ ˉ ) 根 据 三 个 参 数 分 开 = ∑ I log ( π i 1 ) P ( O , I ∣ λ ˉ ) + ∑ I ( ∑ t = 1 T − 1 log a i t , i t + 1 ) P ( O , I ∣ λ ˉ ) + ∑ I ( ∑ t = 1 T b i t ( o t ) ) P ( O , I ∣ λ ˉ ) (10.34) \begin{aligned} Q(\lambda,\bar \lambda) &= \sum_I \log P(O,I|\lambda)P(O,I|\bar \lambda) \\ &= \sum_I \log [ \pi_{i_1} b_{i_1}(o_1)a_{i_1,i_2}b_{i_2}(o_2)\cdots a_{i_{T-1},i_T}b_{i_T}(o_T)]P(O,I|\bar \lambda) \\ &= \sum_I [\log(\pi_{i_1}) + \log(a_{i_1,i_2}a_{i_2,i_3}a_{i_{T-1},i_T}) + \log(b_{i_1}(o_1)b_{i_2}(o_2)\cdots b_{i_T}(o_T) ] P(O,I|\bar \lambda) & 根据三个参数分开\\ &=\sum_I \log (\pi_{i_1}) P(O,I|\bar \lambda) + \sum_I \left( \sum_{t=1}^{T-1} \log a_{i_t,i_{t+1}} \right) P(O,I|\bar \lambda) + \sum_I \left( \sum_{t=1}^{T} b_{i_t}(o_t) \right) P(O,I|\bar \lambda) \end{aligned}\tag{10.34} Q(λ,λˉ)=I∑logP(O,I∣λ)P(O,I∣λˉ)=I∑log[πi1bi1(o1)ai1,i2bi2(o2)⋯aiT−1,iTbiT(oT)]P(O,I∣λˉ)=I∑[log(πi1)+log(ai1,i2ai2,i3aiT−1,iT)+log(bi1(o1)bi2(o2)⋯biT(oT)]P(O,I∣λˉ)=I∑log(πi1)P(O,I∣λˉ)+I∑(t=1∑T−1logait,it+1)P(O,I∣λˉ)+I∑(t=1∑Tbit(ot))P(O,I∣λˉ)根据三个参数分开(10.34)
3.EM算法的M步: 极大化 Q Q Q函数 Q ( λ , λ ˉ ) Q(\lambda,\bar \lambda) Q(λ,λˉ) 求模型参数 A , B , π A,B,\pi A,B,π
我们上一步已经把要极大化的参数单独地分开成三个项,所以只需要对各项分别极大化。
(1)式 ( 10.34 ) (10.34) (10.34)第1项可以写成:
∑ I log ( π i 1 ) P ( O , I ∣ λ ˉ ) = ∑ i = 1 N log ( π i ) P ( O , i 1 = i ∣ λ ˉ ) \sum_I \log (\pi_{i_1}) P(O,I|\bar \lambda) = \sum_{i=1}^N \log (\pi_{i}) P(O,i_1=i|\bar \lambda) I∑log(πi1)P(O,I∣λˉ)=i=1∑Nlog(πi)P(O,i1=i∣λˉ)
π i \pi_i πi满足约束条件 ∑ i = 1 N π i = 1 \sum_{i=1}^N \pi_i =1 ∑i=1Nπi=1,利用拉格朗日乘子法,可以写出拉格朗日函数:
∑ i = 1 N log ( π i ) P ( O , i 1 = i ∣ λ ˉ ) + γ ( ∑ i = 1 N π i − 1 ) \sum_{i=1}^N \log (\pi_{i}) P(O,i_1=i|\bar \lambda) + \gamma \left(\sum_{i=1}^N \pi_i -1 \right) i=1∑Nlog(πi)P(O,i1=i∣λˉ)+γ(i=1∑Nπi−1)
上式对 π i \pi_i πi求偏导并令结果为0:
∂ ∂ π i [ ∑ i = 1 N log ( π i ) P ( O , i 1 = i ∣ λ ˉ ) + γ ( ∑ i = 1 N π i − 1 ) ] = 0 (10.35) \frac{\partial}{\partial \pi_i} \left[ \sum_{i=1}^N \log (\pi_{i}) P(O,i_1=i|\bar \lambda) + \gamma \left(\sum_{i=1}^N \pi_i -1 \right) \right] = 0 \tag{10.35} ∂πi∂[i=1∑Nlog(πi)P(O,i1=i∣λˉ)+γ(i=1∑Nπi−1)]=0(10.35)
得
1 π i P ( O , i 1 = i ∣ λ ˉ ) + γ = 0 ⇒ P ( O , i 1 = i ∣ λ ˉ ) + π i γ = 0 \frac{1}{\pi_i} P(O,i_1=i|\bar \lambda) + \gamma = 0 \Rightarrow P(O,i_1=i|\bar \lambda) + \pi_i\gamma = 0 πi1P(O,i1=i∣λˉ)+γ=0⇒P(O,i1=i∣λˉ)+πiγ=0
对 i i i求和得到 γ \gamma γ:
π i γ = − P ( O , i 1 = i ∣ λ ˉ ) ∑ i π i γ = ∑ i − P ( O , i 1 = i ∣ λ ˉ ) γ = − P ( O ∣ λ ˉ ) \begin{aligned} \pi_i\gamma &= -P(O,i_1=i|\bar \lambda) \\ \sum_i \pi_i\gamma &= \sum_i -P(O,i_1=i|\bar \lambda) \\ \gamma &= -P(O|\bar \lambda) \end{aligned} πiγi∑πiγγ=−P(O,i1=i∣λˉ)=i∑−P(O,i1=i∣λˉ)=−P(O∣λˉ)
代入式 ( 10.35 ) (10.35) (10.35)得
P ( O , i 1 = i ∣ λ ˉ ) + π i γ = 0 π i = − P ( O , i 1 = i ∣ λ ˉ ) γ π i = P ( O , i 1 = i ∣ λ ˉ ) P ( O ∣ λ ˉ ) (10.36) \begin{aligned} P&(O,i_1=i|\bar \lambda) + \pi_i\gamma = 0 \\ \pi_i &= -\frac{P(O,i_1=i|\bar \lambda) }{\gamma} \\ \pi_i &= \frac{P(O,i_1=i|\bar \lambda) }{P(O|\bar \lambda)} \end{aligned} \tag{10.36} Pπiπi(O,i1=i∣λˉ)+πiγ=0=−γP(O,i1=i∣λˉ)=P(O∣λˉ)P(O,i1=i∣λˉ)(10.36)
(2) 式 ( 10.34 ) (10.34) (10.34)的第2项可以写成
∑ I ( ∑ t = 1 T − 1 log a i t , i t + 1 ) P ( O , I ∣ λ ˉ ) = ∑ i = 1 N ∑ j = 1 N ∑ t = 1 T − 1 log a i j P ( O , i t = i , i t + 1 = j ∣ λ ˉ ) \sum_I \left( \sum_{t=1}^{T-1} \log a_{i_t,i_{t+1}} \right) P(O,I|\bar \lambda) = \sum_{i=1}^{N} \sum_{j=1}^{N} \sum_{t=1}^{T-1} \log a_{ij} P(O,i_t=i,i_{t+1}=j|\bar \lambda) I∑(t=1∑T−1logait,it+1)P(O,I∣λˉ)=i=1∑Nj=1∑Nt=1∑T−1logaijP(O,it=i,it+1=j∣λˉ)
a i j a_{ij} aij满足约束条件 ∑ j = 1 N a i j = 1 \sum_{j=1}^N a_{ij} =1 ∑j=1Naij=1,利用拉格朗日乘子法,可以写出拉格朗日函数:
∑ i = 1 N ∑ j = 1 N ∑ t = 1 T − 1 log a i j P ( O , i t = i , i t + 1 = j ∣ λ ˉ ) + γ ( ∑ i = 1 N a i j − 1 ) \sum_{i=1}^{N} \sum_{j=1}^{N} \sum_{t=1}^{T-1} \log a_{ij} P(O,i_t=i,i_{t+1}=j|\bar \lambda)+ \gamma \left(\sum_{i=1}^N a_{ij} -1 \right) i=1∑Nj=1∑Nt=1∑T−1logaijP(O,it=i,it+1=j∣λˉ)+γ(i=1∑Naij−1)
上式对 a i j a_{ij} aij求偏导并令结果为0得:
1 a i j ∑ t = 1 T − 1 P ( O , i t = i , i t + 1 = j ∣ λ ˉ ) + γ = 0 a i j γ = − ∑ t = 1 T − 1 P ( O , i t = i , i t + 1 = j ∣ λ ˉ ) \frac{1}{a_{ij}} \sum_{t=1}^{T-1} P(O,i_t=i,i_{t+1}=j|\bar \lambda) +\gamma = 0 \\ a_{ij}\gamma = - \sum_{t=1}^{T-1} P(O,i_t=i,i_{t+1}=j|\bar \lambda) aij1t=1∑T−1P(O,it=i,it+1=j∣λˉ)+γ=0aijγ=−t=1∑T−1P(O,it=i,it+1=j∣λˉ)
两边对 j j j求和:
∑ j a i j γ = − ∑ j ∑ t = 1 T − 1 P ( O , i t = i , i t + 1 = j ∣ λ ˉ ) γ = − ∑ t = 1 T − 1 P ( O , i t = i ∣ λ ˉ ) \sum_j a_{ij} \gamma = -\sum_j \sum_{t=1}^{T-1} P(O,i_t=i,i_{t+1}=j|\bar \lambda) \\ \gamma = - \sum_{t=1}^{T-1} P(O,i_t=i|\bar \lambda) j∑aijγ=−j∑t=1∑T−1P(O,it=i,it+1=j∣λˉ)γ=−t=1∑T−1P(O,it=i∣λˉ)
代入得
a i j = ∑ t = 1 T − 1 P ( O , i t = i , i t + 1 = j ∣ λ ˉ ) ∑ t = 1 T − 1 P ( O , i t = i ∣ λ ˉ ) (10.37) a_{ij} = \frac{ \sum_{t=1}^{T-1} P(O,i_t=i,i_{t+1}=j|\bar \lambda)}{\sum_{t=1}^{T-1} P(O,i_t=i|\bar \lambda)} \tag{10.37} aij=∑t=1T−1P(O,it=i∣λˉ)∑t=1T−1P(O,it=i,it+1=j∣λˉ)(10.37)
(3) 式 ( 10.34 ) (10.34) (10.34)的第3项为
∑ I ( ∑ t = 1 T b i t ( o t ) ) P ( O , I ∣ λ ˉ ) = ∑ j = 1 N ∑ t = 1 T log b j ( o t ) P ( O , i t = j ∣ λ ˉ ) \sum_I \left( \sum_{t=1}^{T} b_{i_t}(o_t) \right) P(O,I|\bar \lambda) = \sum_{j=1}^N \sum_{t=1}^T \log b_j(o_t) P(O,i_t=j|\bar \lambda) I∑(t=1∑Tbit(ot))P(O,I∣λˉ)=j=1∑Nt=1∑Tlogbj(ot)P(O,it=j∣λˉ)
约束条件是 ∑ k = 1 M b j ( k ) = 1 \sum_{k=1}^M b_j(k)=1 ∑k=1Mbj(k)=1,回顾一下,有 M M M个观测变量; b j ( k ) b_j(k) bj(k)表示状态为 q j q_j qj的情况下观测为 v k v_k vk的概率。
注意,只有在 o t = v k o_t=v_k ot=vk时 b j ( o t ) b_j(o_t) bj(ot)对 b j ( k ) b_j(k) bj(k)的偏导数才不为0,以 I ( o t = v k ) I(o_t=v_k) I(ot=vk)表示。
利用拉格朗日乘子法,写出拉格朗日函数:
∑ j = 1 N ∑ t = 1 T log b j ( o t ) P ( O , i t = j ∣ λ ˉ ) + γ ( ∑ k = 1 M b j ( k ) − 1 ) \sum_{j=1}^N \sum_{t=1}^T \log b_j(o_t) P(O,i_t=j|\bar \lambda) + \gamma \left(\sum_{k=1}^M b_j(k) -1 \right) j=1∑Nt=1∑Tlogbj(ot)P(O,it=j∣λˉ)+γ(k=1∑Mbj(k)−1)
上式对 b j ( k ) b_j(k) bj(k)求偏导并令结果为0得:
1 b j ( k ) ∑ t = 1 T P ( O , i t = j ∣ λ ˉ ) I ( o t = v k ) + γ = 0 b j ( k ) γ = − ∑ t = 1 T P ( O , i t = j ∣ λ ˉ ) I ( o t = v k ) \frac{1}{b_j(k)} \sum_{t=1}^T P(O,i_t=j|\bar \lambda) I(o_t=v_k) + \gamma = 0 \\ b_j(k) \gamma = -\sum_{t=1}^T P(O,i_t=j|\bar \lambda) I(o_t=v_k) bj(k)1t=1∑TP(O,it=j∣λˉ)I(ot=vk)+γ=0bj(k)γ=−t=1∑TP(O,it=j∣λˉ)I(ot=vk)
两边对 k k k求和,注意右边本来通过指示函数 I ( o t = v k ) I(o_t=v_k) I(ot=vk)限制 o t = v k o_t=v_k ot=vk,对 k k k求和的话,相当于整个指示函数没了。
γ = − ∑ t = 1 T P ( O , i t = j ∣ λ ˉ ) \gamma =-\sum_{t=1}^T P(O,i_t=j|\bar \lambda) γ=−t=1∑TP(O,it=j∣λˉ)
代入得
b j ( k ) = ∑ t = 1 T P ( O , i t = j ∣ λ ˉ ) I ( o t = v k ) ∑ t = 1 T P ( O , i t = j ∣ λ ˉ ) (10.38) b_j(k) = \frac{\sum_{t=1}^T P(O,i_t=j|\bar \lambda) I(o_t=v_k)}{\sum_{t=1}^T P(O,i_t=j|\bar \lambda)} \tag{10.38} bj(k)=∑t=1TP(O,it=j∣λˉ)∑t=1TP(O,it=j∣λˉ)I(ot=vk)(10.38)
Baum-Welch模型参数估计公式
将式 ( 10.36 ) (10.36) (10.36)~式 ( 10.38 ) (10.38) (10.38)中的各概率分别用式 ( 10.23 ) , ( 10.25 ) (10.23),(10.25) (10.23),(10.25)中的 γ t ( i ) , ξ t ( i , j ) \gamma_t(i),\xi_t(i,j) γt(i),ξt(i,j)表示,则可以写成:
a i j = ∑ t = 1 T − 1 P ( O , i t = i , i t + 1 = j ∣ λ ˉ ) ∑ t = 1 T − 1 P ( O , i t = i ∣ λ ˉ ) = ∑ t = 1 T − 1 P ( i t = i , i t + 1 = j ∣ O , λ ˉ ) P ( O ∣ λ ˉ ) ∑ t = 1 T − 1 P ( O , i t = i ∣ λ ˉ ) = ∑ t = 1 T − 1 P ( i t = i , i t + 1 = j ∣ O , λ ˉ ) ∑ t = 1 T − 1 P ( O , i t = i ∣ λ ˉ ) / P ( O ∣ λ ˉ ) = ∑ t = 1 T − 1 ξ t ( i , j ) ∑ t = 1 T − 1 γ t ( i ) (10.39) \begin{aligned} a_{ij} &= \frac{ \sum_{t=1}^{T-1} P(O,i_t=i,i_{t+1}=j|\bar \lambda)}{\sum_{t=1}^{T-1} P(O,i_t=i|\bar \lambda)} \\&= \frac{\sum_{t=1}^{T-1} P(i_t=i,i_{t+1}=j|O,\bar \lambda)P(O|\bar \lambda)}{\sum_{t=1}^{T-1} P(O,i_t=i|\bar \lambda) } \\ &= \frac{\sum_{t=1}^{T-1} P(i_t=i,i_{t+1}=j|O,\bar \lambda)}{\sum_{t=1}^{T-1} P(O,i_t=i|\bar \lambda) / P(O|\bar \lambda) } \\ &= \frac{\sum_{t=1}^{T-1} \xi_t(i,j)}{\sum_{t=1}^{T-1} \gamma_t(i)} \end{aligned} \tag{10.39} aij=∑t=1T−1P(O,it=i∣λˉ)∑t=1T−1P(O,it=i,it+1=j∣λˉ)=∑t=1T−1P(O,it=i∣λˉ)∑t=1T−1P(it=i,it+1=j∣O,λˉ)P(O∣λˉ)=∑t=1T−1P(O,it=i∣λˉ)/P(O∣λˉ)∑t=1T−1P(it=i,it+1=j∣O,λˉ)=∑t=1T−1γt(i)∑t=1T−1ξt(i,j)(10.39)
b j ( k ) = ∑ t = 1 T P ( O , i t = j ∣ λ ˉ ) I ( o t = v k ) ∑ t = 1 T P ( O , i t = j ∣ λ ˉ ) = ∑ t = 1 T P ( i t = j ∣ O , λ ˉ ) I ( o t = v k ) ∑ t = 1 T P ( i t = j ∣ O , λ ˉ ) = ∑ t = 1 , o t = v k T γ t ( j ) ∑ t = 1 T γ t ( j ) (10.40) \begin{aligned} b_j(k) &= \frac{\sum_{t=1}^T P(O,i_t=j|\bar \lambda) I(o_t=v_k)}{\sum_{t=1}^T P(O,i_t=j|\bar \lambda)} \\ &= \frac{\sum_{t=1}^T P(i_t=j|O,\bar \lambda) I(o_t=v_k)}{\sum_{t=1}^T P(i_t=j|O,\bar \lambda)} \\ &= \frac{\sum_{t=1,o_t=v_k}^T \gamma_t(j)}{\sum_{t=1}^T \gamma_t(j)} \end{aligned} \tag{10.40} bj(k)=∑t=1TP(O,it=j∣λˉ)∑t=1TP(O,it=j∣λˉ)I(ot=vk)=∑t=1TP(it=j∣O,λˉ)∑t=1TP(it=j∣O,λˉ)I(ot=vk)=∑t=1Tγt(j)∑t=1,ot=vkTγt(j)(10.40)
π i = γ 1 ( i ) (10.41) \pi_i = \gamma_1(i) \tag{10.41} πi=γ1(i)(10.41)
然后就可以基于这种形式得到Baum-Welch算法的步骤。
预测算法
预算算法是用来解决预测问题的,即给定模型参数和观测序列,求出最有可能的状态序列。
近似算法
近似算法的思想是,在每个时刻 t t t选择在该时刻最有可能出现的状态 i t ∗ i_t^* it∗,从而得到一个状态序列 I ∗ = ( i 1 ∗ , i 2 ∗ , ⋯ , i T ∗ ) I^*=(i_1^*,i_2^*,\cdots,i_T^*) I∗=(i1∗,i2∗,⋯,iT∗),将它作为预测的结果。
(从式 ( 10.24 ) (10.24) (10.24))给定隐马尔可夫模型 λ \lambda λ和观测序列 O O O,在时刻 t t t处于状态 q i q_i qi的概率 γ t ( i ) \gamma_t(i) γt(i)是
γ t ( i ) = α t ( i ) β t ( i ) P ( O ∣ λ ) = α t ( i ) β t ( i ) ∑ j = 1 N α t ( i ) β t ( i ) (10.42) \gamma_t(i) = \frac{\alpha_t(i)\beta_t(i)}{P(O|\lambda)} = \frac{\alpha_t(i)\beta_t(i)}{\sum_{j=1}^N \alpha_t(i)\beta_t(i)} \tag{10.42} γt(i)=P(O∣λ)αt(i)βt(i)=∑j=1Nαt(i)βt(i)αt(i)βt(i)(10.42)
在每一时刻 t t t最有可能的状态 i t ∗ i^*_t it∗是
i t ∗ = arg max 1 ≤ i ≤ N [ γ t ( i ) ] , t = 1 , 2 , ⋯ , T (10.43) i^*_t = \arg \max_{1 \leq i \leq N} [\gamma_t(i)],\quad t=1,2,\cdots,T \tag{10.43} it∗=arg1≤i≤Nmax[γt(i)],t=1,2,⋯,T(10.43)
从而得到状态序列 I ∗ = ( i 1 ∗ , i 2 ∗ , ⋯ , i T ∗ ) I^* = (i^*_1,i^*_2,\cdots,i^*_T) I∗=(i1∗,i2∗,⋯,iT∗)。
近似算法的优点是计算简单,缺点是不能保证预测的状态序列整体是最有可能的状态序列。
维特比算法
维特比算法实际是用动态规划解决隐马尔可夫模型预测问题,即用动态规划求概率最大路径(最优路径)。这时一条路径对应着一个状态序列。
依据动态规划原理,我们从时刻 t = 1 t=1 t=1开始,递推地计算在时刻 t t t状态为 i i i的各条部分路径的最大概率,直到得到时刻 t = T t=T t=T状态为 i i i的各条路径的最大概率。然后,在时刻 t = T t=T t=T的最大概率即为最优路径的概率 P ∗ P^* P∗,最优路径的终结点 i T ∗ i_T^* iT∗也同时得到。然后从终结点开始,由后向前逐步求得结点 i T − 1 ∗ , ⋯ , i 1 ∗ i^*_{T-1},\cdots,i_1^* iT−1∗,⋯,i1∗,得到最优路径。
首先导入两个变量 δ \delta δ和 Ψ \Psi Ψ,定义在时刻 t t t状态为 i i i的所有单个路径 ( i 1 , i 2 , ⋯ , i t ) (i_1,i_2,\cdots,i_t) (i1,i2,⋯,it)中概率最大值为
δ t ( i ) = max i 1 , ⋯ , i t − 1 P ( i t = i , i t − 1 , ⋯ , i 1 , o t , ⋯ , o 1 ∣ λ ) , i = 1 , 2 , ⋯ , N (10.44) \delta_t(i) = \max_{i_1,\cdots,i_{t-1}} P(i_t=i,i_{t-1},\cdots,i_1,o_t,\cdots,o_1|\lambda),\quad i=1,2,\cdots,N \tag{10.44} δt(i)=i1,⋯,it−1maxP(it=i,it−1,⋯,i1,ot,⋯,o1∣λ),i=1,2,⋯,N(10.44)
由定义可得变量 δ \delta δ的递推公式:
δ t + 1 ( i ) = max i 1 , ⋯ , i t P ( i t + 1 = i , i t , ⋯ , i 1 , o t + 1 , ⋯ , o 1 ∣ λ ) = max i 1 , ⋯ , i t − 1 , i t P ( i t + 1 = i , i t , ⋯ , i 1 , o t + 1 , ⋯ , o 1 ∣ λ ) = max 1 ≤ j ≤ N max i 1 , ⋯ , i t − 1 P ( i t + 1 = i , i t = j , ⋯ , i 1 , o t + 1 , ⋯ , o 1 ∣ λ ) = max 1 ≤ j ≤ N max i 1 , ⋯ , i t − 1 P ( o t + 1 , i t + 1 = i ∣ i t = j , ⋯ , i 1 , o t , ⋯ , o 1 , λ ) P ( i t = j , ⋯ , i 1 , o t , ⋯ , o 1 ∣ λ ) = max 1 ≤ j ≤ N δ t ( j ) P ( o t + 1 , i t + 1 = i ∣ i t = j , ⋯ , i 1 , o t , ⋯ , o 1 , λ ) = max 1 ≤ j ≤ N δ t ( j ) P ( o t + 1 , i t + 1 = i ∣ i t = j , λ ) D − 划 分 = max 1 ≤ j ≤ N δ t ( j ) P ( o t + 1 ∣ i t + 1 = i , i t = j , λ ) P ( i t + 1 = i ∣ i t = j , λ ) = max 1 ≤ j ≤ N δ t ( j ) P ( o t + 1 ∣ i t + 1 = i , λ ) P ( i t + 1 = i ∣ i t = j , λ ) = max 1 ≤ j ≤ N δ t ( j ) b i ( o t + 1 ) a j i = max 1 ≤ j ≤ N [ δ t ( j ) a j i ] b i ( o t + 1 ) , i = 1 , 2 , ⋯ , N ; t = 1 , 2 , ⋯ , T − 1 (10.45) \begin{aligned} \delta_{t+1}(i) &= \max_{i_1,\cdots,i_{t}} P(i_{t+1}=i,i_{t},\cdots,i_1,o_{t+1},\cdots,o_1|\lambda) \\ &= \max_{i_1,\cdots,i_{t-1},i_t} P(i_{t+1}=i,i_{t},\cdots,i_1,o_{t+1},\cdots,o_1|\lambda) \\ &= \max_{1 \leq j \leq N} \max_{i_1,\cdots,i_{t-1}} P(i_{t+1}=i,i_{t}=j,\cdots,i_1,o_{t+1},\cdots,o_1|\lambda) \\ &= \max_{1 \leq j \leq N} \max_{i_1,\cdots,i_{t-1}} P(o_{t+1},i_{t+1}=i|i_{t}=j,\cdots,i_1,o_{t},\cdots,o_1,\lambda) P(i_{t}=j,\cdots,i_1,o_{t},\cdots,o_1|\lambda)\\ &= \max_{1 \leq j \leq N} \delta_t(j) P(o_{t+1},i_{t+1}=i|i_{t}=j,\cdots,i_1,o_{t},\cdots,o_1,\lambda) \\ &= \max_{1 \leq j \leq N} \delta_t(j) P(o_{t+1},i_{t+1}=i|i_{t}=j,\lambda) & D-划分\\ &= \max_{1 \leq j \leq N} \delta_t(j) P(o_{t+1}|i_{t+1}=i,i_{t}=j,\lambda)P(i_{t+1}=i|i_{t}=j,\lambda) \\ &= \max_{1 \leq j \leq N} \delta_t(j) P(o_{t+1}|i_{t+1}=i,\lambda)P(i_{t+1}=i|i_{t}=j,\lambda) \\ &= \max_{1 \leq j \leq N} \delta_t(j) b_{i}(o_{t+1})a_{ji} \\ &= \max_{1 \leq j \leq N} [\delta_t(j)a_{ji}] b_{i}(o_{t+1}) ,\quad i=1,2,\cdots,N;\quad t=1,2,\cdots,T-1 \end{aligned} \tag{10.45} δt+1(i)=i1,⋯,itmaxP(it+1=i,it,⋯,i1,ot+1,⋯,o1∣λ)=i1,⋯,it−1,itmaxP(it+1=i,it,⋯,i1,ot+1,⋯,o1∣λ)=1≤j≤Nmaxi1,⋯,it−1maxP(it+1=i,it=j,⋯,i1,ot+1,⋯,o1∣λ)=1≤j≤Nmaxi1,⋯,it−1maxP(ot+1,it+1=i∣it=j,⋯,i1,ot,⋯,o1,λ)P(it=j,⋯,i1,ot,⋯,o1∣λ)=1≤j≤Nmaxδt(j)P(ot+1,it+1=i∣it=j,⋯,i1,ot,⋯,o1,λ)=1≤j≤Nmaxδt(j)P(ot+1,it+1=i∣it=j,λ)=1≤j≤Nmaxδt(j)P(ot+1∣it+1=i,it=j,λ)P(it+1=i∣it=j,λ)=1≤j≤Nmaxδt(j)P(ot+1∣it+1=i,λ)P(it+1=i∣it=j,λ)=1≤j≤Nmaxδt(j)bi(ot+1)aji=1≤j≤Nmax[δt(j)aji]bi(ot+1),i=1,2,⋯,N;t=1,2,⋯,T−1D−划分(10.45)
P ( o t + 1 , i t + 1 = i ∣ i t = j , ⋯ , i 1 , o t , ⋯ , o 1 , λ ) = P ( o t + 1 , i t + 1 = i ∣ i t = j , λ ) P(o_{t+1},i_{t+1}=i|i_{t}=j,\cdots,i_1,o_{t},\cdots,o_1,\lambda)=P(o_{t+1},i_{t+1}=i|i_{t}=j,\lambda) P(ot+1,it+1=i∣it=j,⋯,i1,ot,⋯,o1,λ)=P(ot+1,it+1=i∣it=j,λ)利用了D-划分:
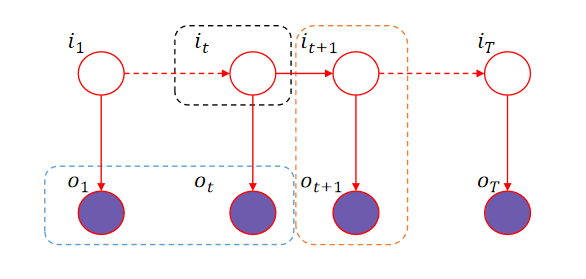
维特比算法很像前向算法除了前者取上个时刻路径概率的最大值,而后者取的是求和。
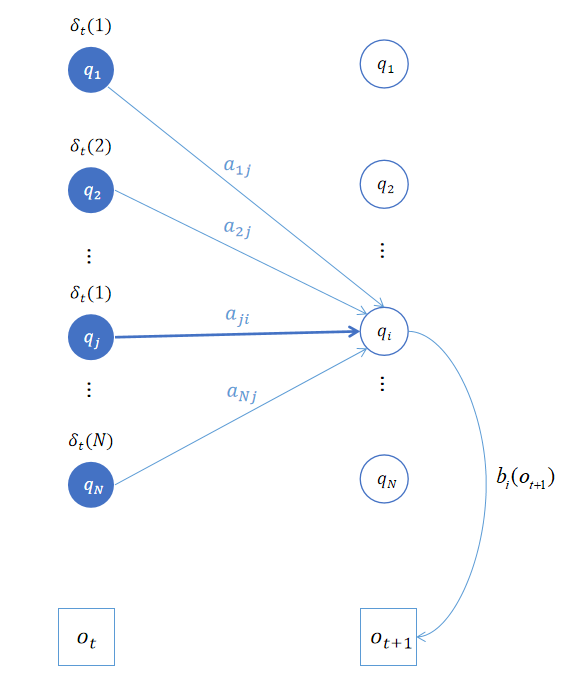
该递推公式除了通过推导,还可以通过画图来理解。如上图所示,已知 t t t时刻各个状态下的 δ t ( j ) , 1 ≤ j ≤ N \delta_t(j),\,\, 1\leq j\leq N δt(j),1≤j≤N。那么 δ t + 1 ( i ) \delta_{t+1}(i) δt+1(i)即在 t t t时刻状态为 j j j的 δ t ( j ) \delta_t(j) δt(j)乘以由状态 j j j转移到 t + 1 t+1 t+1时刻状态 i i i的概率的最大者,再乘以由状态 i i i观测到输出 o t + 1 o_{t+1} ot+1的概率。
定义在时刻 t t t状态为 i i i的所有单个路径 ( i 1 , i 2 , ⋯ , i t ) (i_1,i_2,\cdots,i_t) (i1,i2,⋯,it)中概率最大的路径的第 t − 1 t-1 t−1个结点为
Ψ t ( i ) = arg max 1 ≤ j ≤ N [ δ t ( j ) a j i ] , i = 1 , 2 , ⋯ , N (10.46) \Psi_t(i) = \arg \max_{1 \leq j \leq N} [\delta_t(j)a_{ji}],\quad i=1,2,\cdots,N \tag{10.46} Ψt(i)=arg1≤j≤Nmax[δt(j)aji],i=1,2,⋯,N(10.46)
算法 10.5 (维特比算法)
输入: 模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)和观测 O = ( o 1 , o 2 , ⋯ , o T ) O=(o_1,o_2,\cdots,o_T) O=(o1,o2,⋯,oT);
输出: 最优路径 I ∗ = ( i 1 ∗ , i 2 ∗ , ⋯ , i T ∗ ) I^* = (i^*_1,i^*_2,\cdots,i^*_T) I∗=(i1∗,i2∗,⋯,iT∗)。
(1) 初始化
δ 1 ( i ) = π i b i ( o 1 ) , i = 1 , 2 , ⋯ , N Ψ 1 ( i ) = 0 , i = 1 , 2 , ⋯ , N \delta_1(i) = \pi_ib_i(o_1), \quad i=1,2,\cdots,N \\ \Psi_1(i) = 0, \quad i=1,2,\cdots,N δ1(i)=πibi(o1),i=1,2,⋯,NΨ1(i)=0,i=1,2,⋯,N
在时刻 t = 1 t=1 t=1状态为 i i i的概率最大值即为初始概率乘以 b i ( o 1 ) b_i(o_1) bi(o1), Ψ 1 ( i ) = 0 \Psi_1(i)=0 Ψ1(i)=0表示未知,或者说后面回溯时的终止条件。
(2) 递推。对 t = 2 , 3 , ⋯ , T t=2,3,\cdots,T t=2,3,⋯,T
δ t ( i ) = max 1 ≤ j ≤ N [ δ t − 1 ( j ) a j i ] b i ( o t ) , i = 1 , 2 , ⋯ , N Ψ t ( i ) = arg max 1 ≤ j ≤ N [ δ t − 1 ( j ) a j i ] , i = 1 , 2 , ⋯ , N \delta_t(i) = \max_{1 \leq j \leq N} [\delta_{t-1}(j)a_{ji}]b_i(o_{t}),\quad i=1,2,\cdots,N \\ \Psi_t(i) = \arg \max_{1 \leq j \leq N} [\delta_{t-1}(j)a_{ji}],\quad i=1,2,\cdots,N δt(i)=1≤j≤Nmax[δt−1(j)aji]bi(ot),i=1,2,⋯,NΨt(i)=arg1≤j≤Nmax[δt−1(j)aji],i=1,2,⋯,N
根据递归公式由前一时刻的最大值来计算当前时刻。
(3) 终止
终止就是计算各个状态的最大概率:
P ∗ = max 1 ≤ i ≤ N δ T ( i ) i T ∗ = arg max 1 ≤ i ≤ N [ δ T ( i ) ] P^* = \max_{1 \leq i \leq N} \delta_T(i) \\ i^*_T = \arg \max_{1 \leq i \leq N} [\delta_T(i)] P∗=1≤i≤NmaxδT(i)iT∗=arg1≤i≤Nmax[δT(i)]
(4) 最优路径回溯。对 t = T − 1 , T − 2 , ⋯ , 1 t=T-1,T-2,\cdots,1 t=T−1,T−2,⋯,1
上一步得到的 T T T时刻的终结点,然后从 T − 1 T-1 T−1时刻利用 i T − 1 ∗ = Ψ T ( i T ∗ ) i^*_{T-1}=\Psi_{T}(i^*_{T}) iT−1∗=ΨT(iT∗)求得 T T T时刻状态为 i T ∗ i^*_T iT∗概率最大路径的前一个时刻最优结点 i T − 1 ∗ i^*_{T-1} iT−1∗,以此类推:
i t ∗ = Ψ t + 1 ( i t + 1 ∗ ) i_t^* = \Psi_{t+1}(i^*_{t+1}) it∗=Ψt+1(it+1∗)
求得最优路径 I ∗ = ( i 1 ∗ , i 2 ∗ , ⋯ , i T ∗ ) I^*=(i_1^*,i_2^*,\cdots,i_T^*) I∗=(i1∗,i2∗,⋯,iT∗)。
下面通过书上的例子,并画图来理解一下维特比算法。
例 10.3 已知模型参数 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)和观测序列 O = ( 红 , 白 , 红 ) O=(红,白,红) O=(红,白,红),试求最优状态序列,即最优路径。
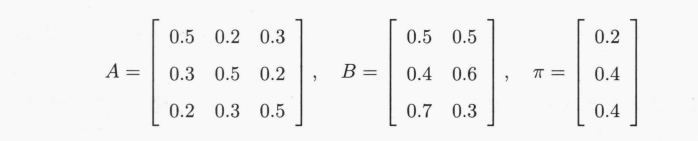
按照上面介绍的维特比算法一步一步来求。
对于 t = 1 t=1 t=1,即初始化时,对所有的状态 i ( i = 1 , 2 , 3 ) i\,\,(i=1,2,3) i(i=1,2,3)求状态为 i i i观测 o 1 o_1 o1为红球的概率 δ 1 ( i ) \delta_1(i) δ1(i):
δ 1 ( 1 ) = π 1 b 1 ( o 1 ) = 0.2 × 0.5 = 0.10 δ 1 ( 2 ) = π 2 b 2 ( o 1 ) = 0.4 × 0.4 = 0.16 δ 1 ( 3 ) = π 3 b 3 ( o 1 ) = 0.4 × 0.7 = 0.28 \delta_1(1) = \pi_1b_1(o_1) = 0.2 \times 0.5 = 0.10 \\ \delta_1(2) = \pi_2b_2(o_1) = 0.4 \times 0.4 = 0.16 \\ \delta_1(3) = \pi_3b_3(o_1) = 0.4 \times 0.7 = 0.28 δ1(1)=π1b1(o1)=0.2×0.5=0.10δ1(2)=π2b2(o1)=0.4×0.4=0.16δ1(3)=π3b3(o1)=0.4×0.7=0.28
且 Ψ 1 ( i ) = 0 , i = 1 , 2 , 3 \Psi_1(i) = 0, \quad i=1,2,3 Ψ1(i)=0,i=1,2,3。
此时,如下图所示:

对于 t = 2 t=2 t=2,对所有的状态 i ( i = 1 , 2 , 3 ) i\,\,(i=1,2,3) i(i=1,2,3)求状态为 i i i观测 o 2 o_2 o2为白球的概率 δ 2 ( i ) \delta_2(i) δ2(i)。
对于 i = 1 i=1 i=1有:
δ 2 ( 1 ) = max 1 ≤ j ≤ 3 [ δ 1 ( j ) a j 1 ] b 1 ( o 2 ) = max [ 0.1 × 0.5 , 0.16 × 0.3 , 0.28 × 0.2 ] × 0.5 = 0.056 × 0.5 = 0.028 \delta_2(1) = \max_{1 \leq j \leq 3} [\delta_{1}(j)a_{j1}]b_1(o_{2}) = \max [0.1 \times 0.5,0.16 \times 0.3,0.28 \times 0.2] \times 0.5 = 0.056 \times 0.5 = 0.028 δ2(1)=1≤j≤3max[δ1(j)aj1]b1(o2)=max[0.1×0.5,0.16×0.3,0.28×0.2]×0.5=0.056×0.5=0.028
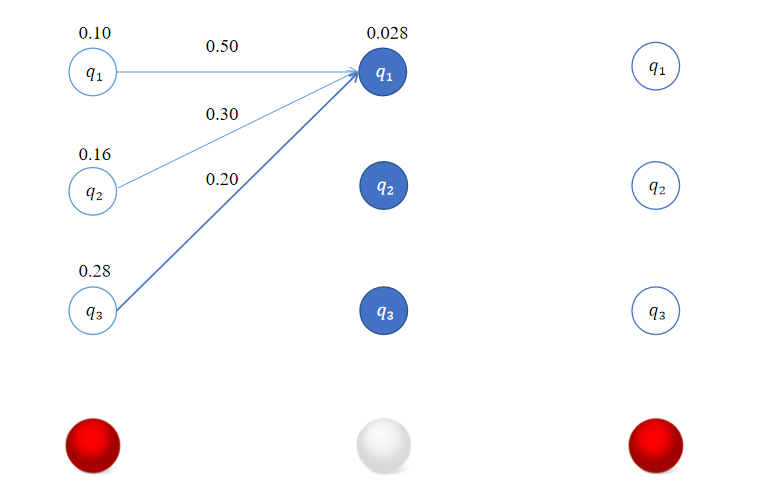
类似地,对于 i = 2 i=2 i=2有:
δ 2 ( 2 ) = max 1 ≤ j ≤ 3 [ δ 1 ( j ) a j 2 ] b 2 ( o 2 ) = max [ 0.1 × 0.2 , 0.16 × 0.5 , 0.28 × 0.3 ] × 0.6 = 0.084 × 0.6 = 0.0504 \delta_2(2) = \max_{1 \leq j \leq 3} [\delta_{1}(j)a_{j2}]b_2(o_{2}) = \max [0.1\times 0.2,0.16 \times 0.5,0.28 \times 0.3] \times 0.6 = 0.084 \times 0.6 = 0.0504 δ2(2)=1≤j≤3max[δ1(j)aj2]b2(o2)=max[0.1×0.2,0.16×0.5,0.28×0.3]×0.6=0.084×0.6=0.0504
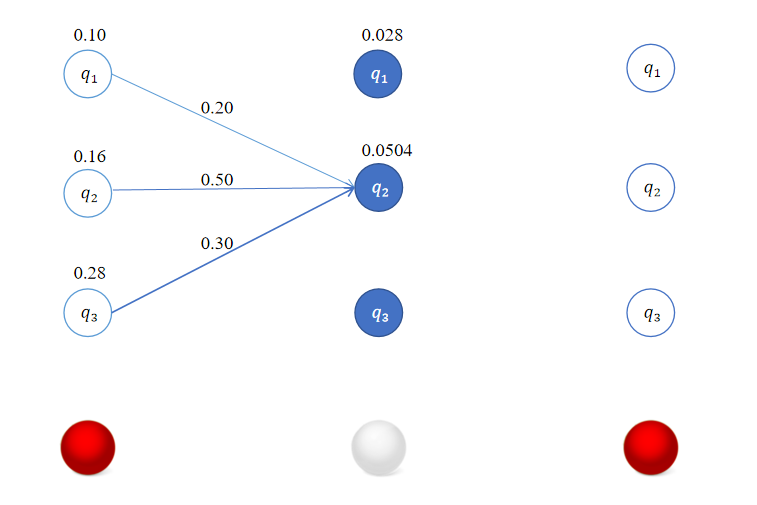
对于 i = 3 i=3 i=3有:
δ 2 ( 3 ) = max 1 ≤ j ≤ 3 [ δ 1 ( j ) a j 3 ] b 3 ( o 2 ) = max [ 0.1 × 0.3 , 0.16 × 0.2 , 0.28 × 0.5 ] × 0.3 = 0.14 × 0.3 = 0.042 \delta_2(3) = \max_{1 \leq j \leq 3} [\delta_{1}(j)a_{j3}]b_3(o_{2}) = \max [0.1\times 0.3,0.16 \times 0.2,0.28 \times 0.5] \times 0.3 = 0.14 \times 0.3 = 0.042 δ2(3)=1≤j≤3max[δ1(j)aj3]b3(o2)=max[0.1×0.3,0.16×0.2,0.28×0.5]×0.3=0.14×0.3=0.042
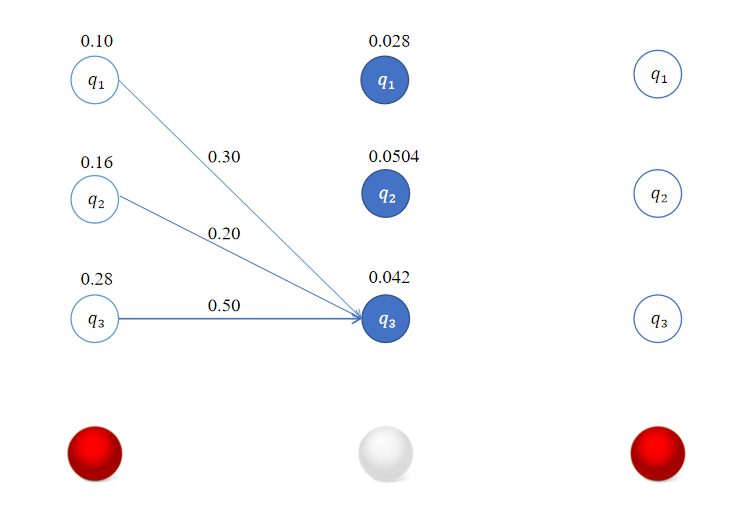
这样我们得到了在时刻 t = 2 t=2 t=2时,转移到各个状态的最优路径,这里恰巧它们都是从 t = 1 t=1 t=1时状态 q 3 q_3 q3出发的。
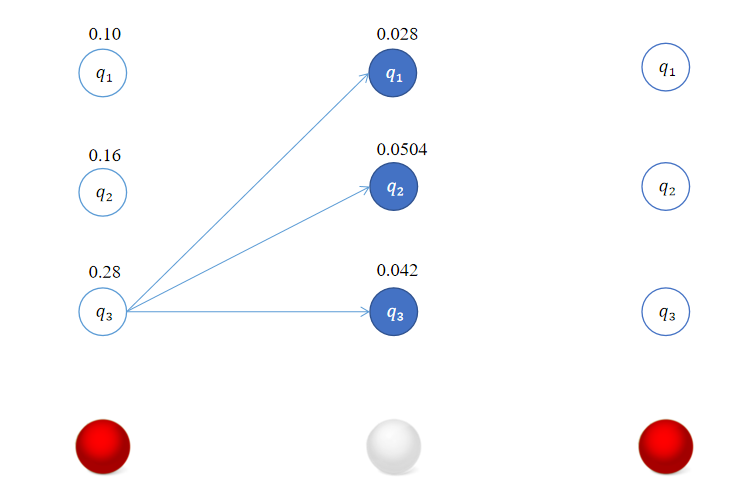
同理,对于 t = 3 t=3 t=3,对所有的状态 i ( i = 1 , 2 , 3 ) i\,\,(i=1,2,3) i(i=1,2,3)求状态为 i i i观测 o 3 o_3 o3为红球的概率 δ 3 ( i ) \delta_3(i) δ3(i)。
δ 3 ( 1 ) = max 1 ≤ j ≤ 3 [ δ 2 ( j ) a j 1 ] b 1 ( o 3 ) = max [ 0.028 × 0.5 , 0.0504 ‾ × 0.3 , 0.042 × 0.2 ] × 0.5 = 0.01512 × 0.5 = 0.000756 δ 3 ( 2 ) = max 1 ≤ j ≤ 3 [ δ 2 ( j ) a j 2 ] b 2 ( o 3 ) = max [ 0.028 × 0.2 , 0.0504 ‾ × 0.5 , 0.042 × 0.3 ] × 0.4 = 0.02520 × 0.4 = 0.001008 δ 3 ( 3 ) = max 1 ≤ j ≤ 3 [ δ 2 ( j ) a j 3 ] b 3 ( o 3 ) = max [ 0.028 × 0.3 , 0.0504 × 0.2 , 0.042 ‾ × 0.5 ] × 0.7 = 0.02100 × 0.7 = 0.001470 \delta_3(1) = \max_{1 \leq j \leq 3} [\delta_{2}(j)a_{j1}]b_1(o_{3}) = \max [0.028 \times 0.5,\overline{0.0504} \times 0.3,0.042 \times 0.2] \times 0.5 = 0.01512 \times 0.5 = 0.000756 \\ \delta_3(2) = \max_{1 \leq j \leq 3} [\delta_{2}(j)a_{j2}]b_2(o_{3}) = \max [0.028 \times 0.2,\overline{0.0504} \times 0.5,0.042 \times 0.3] \times 0.4 = 0.02520 \times 0.4 = 0.001008 \\ \delta_3(3) = \max_{1 \leq j \leq 3} [\delta_{2}(j)a_{j3}]b_3(o_{3}) = \max [0.028 \times 0.3,0.0504 \times 0.2,\overline{0.042} \times 0.5] \times 0.7 = 0.02100 \times 0.7 = 0.001470 δ3(1)=1≤j≤3max[δ2(j)aj1]b1(o3)=max[0.028×0.5,0.0504×0.3,0.042×0.2]×0.5=0.01512×0.5=0.000756δ3(2)=1≤j≤3max[δ2(j)aj2]b2(o3)=max[0.028×0.2,0.0504×0.5,0.042×0.3]×0.4=0.02520×0.4=0.001008δ3(3)=1≤j≤3max[δ2(j)aj3]b3(o3)=max[0.028×0.3,0.0504×0.2,0.042×0.5]×0.7=0.02100×0.7=0.001470
最终我们得到的结果如下:
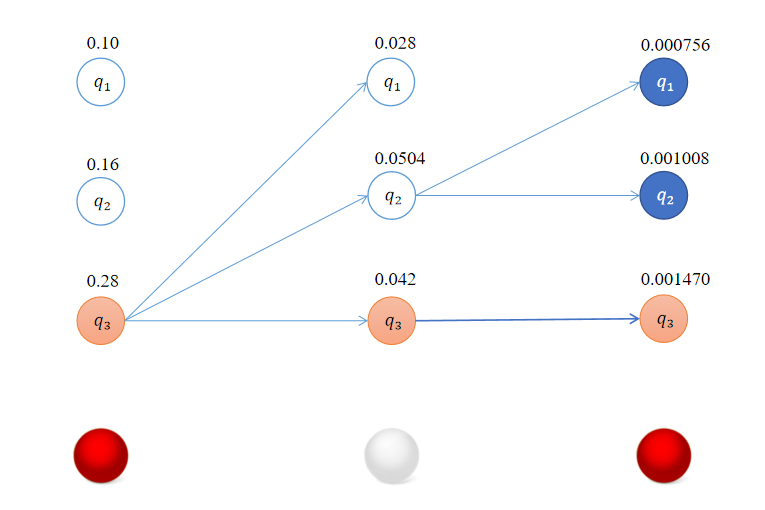
回溯得到最优路径的状态序列 ( q 3 , q 3 , q 3 ) (q_3,q_3,q_3) (q3,q3,q3)。
参考
- 统计学习方法 第二版
- 概率导论
- 维基百科
- PRML
- MLAPP
相关文章:

《统计学习方法》——隐马尔可夫模型(下)
学习算法 HMM的学习,在有观测序列的情况下,根据训练数据是否包含状态序列,可以分别由监督学习算法和无监督学习算法实现。 监督学习算法 监督学习算法就比较简单,基于已有的数据利用极大似然估计法来估计隐马尔可夫模型的参数。…...

Liunx top 命令详解
文章目录 top补充说明语法选项top交互命令实例 top 显示或管理执行中的程序 补充说明 top命令 可以实时动态地查看系统的整体运行情况,是一个综合了多方信息监测系统性能和运行信息的实用工具。通过top命令所提供的互动式界面,用热键可以管理。 语法…...

基于 SpringBoot 的医院固定资产系统
本文将介绍基于 SpringBoot 技术的医院固定资产系统的设计和实现。医院固定资产管理是医疗机构管理工作的重要组成部分,它对医院的正常运营和管理具有重要的意义。本系统的设计和实现将有助于医疗机构更好地管理和维护其固定资产。 1. 系统需求分析 医院固定资产管…...

【企业信息化】第2集 免费开源ERP: Odoo 16 销售管理系统
文章目录 前言一、概览二、使用功能1.通过清晰报价提高销售效率2.创建专业报价单3.管理订单及合同4.简化沟通5.维护产品&价格6.直观的报告7.集成 三、总结 前言 世界排名第一的免费开源ERP: Odoo 16 销售管理系统。通过Odoo Sign应用程序和在线支付,发送报价。…...

浅谈数据治理
大家好 ,近年来,数据治理成为挖掘数据价值的重要手段和工具。随着大数据平台和工业互联网兴起,数据治理平台主要采用数据中台技术和微服务架构初步替代传统架构,面向大数据架构下,为数据资源中心与外部数据系统提供数据…...

Matlab入门教程003|MATLAB变量|MATLAB命令
MATLAB变量 每个MATLAB变量可以是数组或者矩阵。 用一个简单的方法指定变量。例如: x 3 % defining x and initializing it with a value MATLAB执行上述语句,并返回以下结果: x 3 上述的例子创建了一个1-1的矩阵名为x和的值存储…...

【啃书C++Primer5】-编写一个简单C++程序
每个C程序都包含一个或多个函数(function),其中一个必须命名为main。操作系统通过调用main来运行C程序。下面是一个非常简单的main函数,它什么也不干,只是返回给操作系统一个值: int main() {return 0; }一个函数的定义包含四部分:返回类型(r…...
GoView 是一个Vue3搭建的低代码数据可视化开发平台
一、总览 开源、精美、便捷的「数据可视化」低代码开发平台 二、整体介绍 框架:基于 Vue3 框架编写,使用 hooks 写法抽离部分逻辑,使代码结构更加清晰; 类型:使用 TypeScript 进行类型约束,减少未知错误…...

【面试篇】Redis持久化面试题
文章目录 Redis持久化🙎♂️面试官:什么是Redis持久化? AOF日志AOF日志原理🙎♂️面试官:AOF日志是怎么工作的/AOF写入磁盘的流程?🙎♂️面试官: 刚刚说到了Redis先执行写入的…...
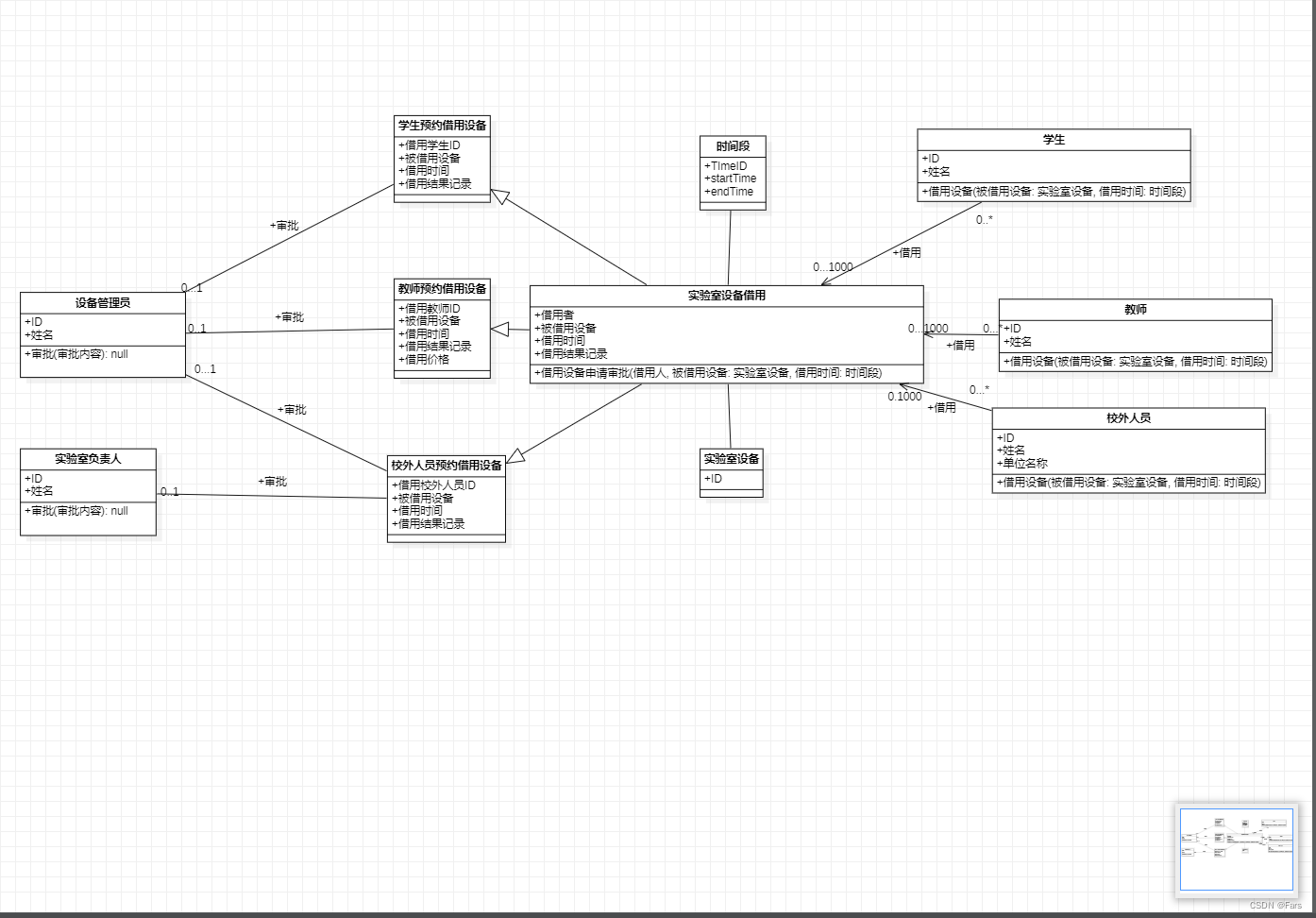
哈工大软件过程与工具作业2
云原生技术云原生技术 哈尔滨工业大学 计算机科学与技术学院/国家示范性软件学院 2022年秋季学期 《软件过程与工具》课程 作业报告 作业 2:需求分析UML建模 姓名 学号 联系方式 石卓凡 120L021011 944613709qq.com/18974330318 目 录 1 需求概述...........…...
)
SDN控制器三平面(软件定义网络、OOB)
目录 又名 三个独立的平面或层 SDN数据流 控制流量的带外(OOB) 优势 技术...

嘉兴桐乡会计考证实操-考初级会计真的有用吗?
一边说着:考初级会计门槛太低了,谁都能考;一边又争先恐后的去报考,考初级会计真的是有用的吗?为什么这么多人一边说考了没用却一直在努力备考呢? 关于这类的话题,其实一直都存在,但不…...

约翰霍普金斯大学诺奖得主涉嫌造假,撤回5篇PNAS论文
2019年,约翰霍普金斯大学的著名基因医学科学家Gregg L. Semenza博士因为“发现细胞如何感知和适应氧气供应”,和另外两名科学家( William Kaelin Jr. and Peter J. Ratcliffe)分享当年的生理医学诺贝尔奖。 近期,Gregg…...
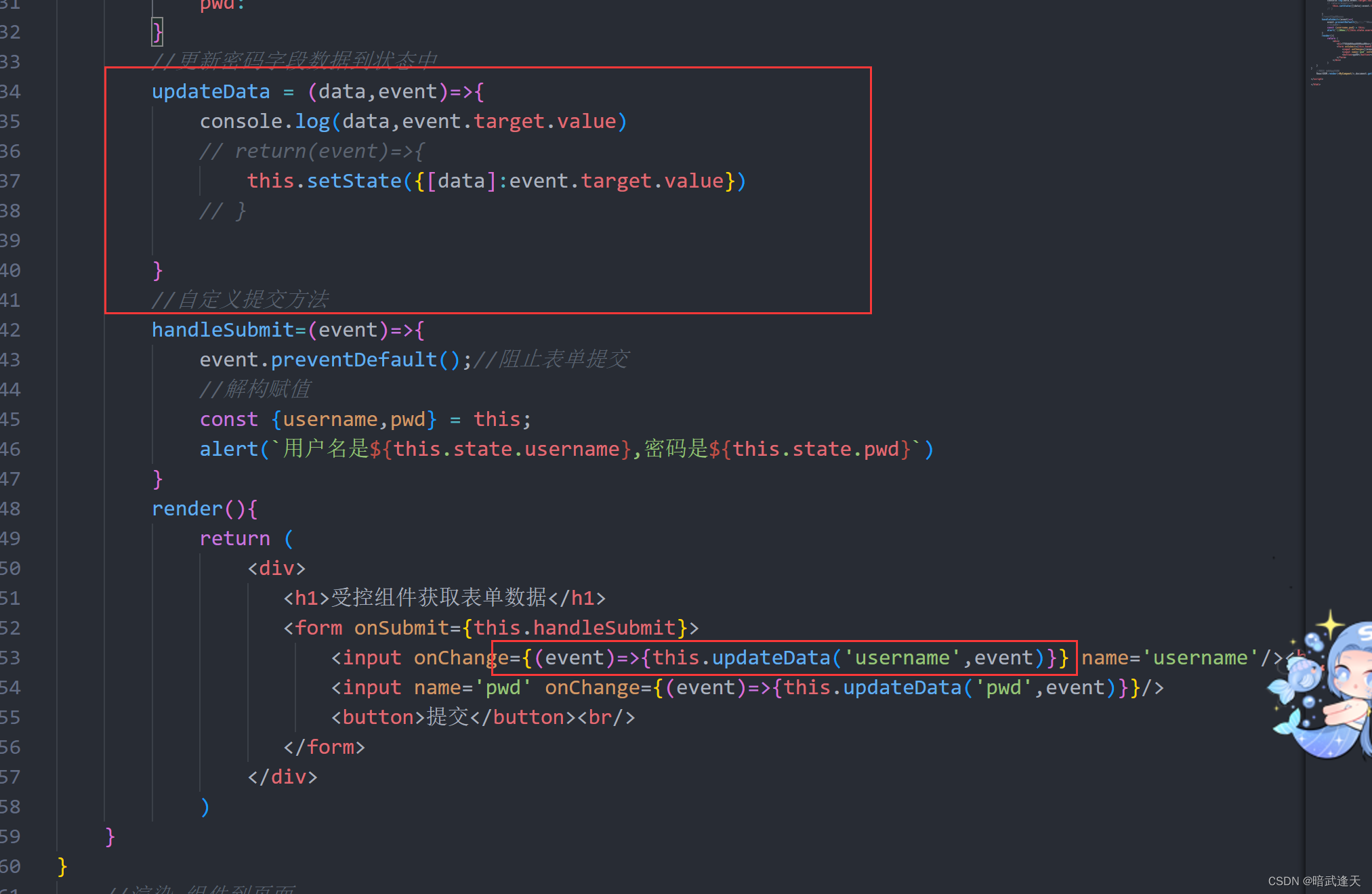
React的表单数据绑定
当我们在页面中使用表单提交数据时,react是如何拿取表单数据的呢 这里通过两种方式来实现 非受控组件实现 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" conte…...

Dubbo——微服务框架(单体式->分布式->微服务)
是什么? Dubbo是阿里巴巴开源的基于Java的高性能RPC(一种远程调用)分布式服务框架,致力于提供高性能和透明化的RPC远程服务调用方案,以及SOA服务治理方案,它提供了三大核心能力:面向接口的远程…...

【Spring Cloud】Feign传递HttpServletRequest
这里我的业务场景是:在请求头中获取服务端登录时传给客户端的token,并且客户端将token放在请求头中。以至于我需要在参数传递上传入HttpServletRequest。如果你非要向我一样传入HttpServletRequest对象那么就往下看,当然你如果可以改成其他参…...
烟火识别智能监测系统 yolov5
烟火识别智能监测系统基于pythonyolov5网络模型算法智能分析技术,烟火识别智能监测算法模型对现场画面进行实时分析,发现现场出现烟火立即抓拍实时告警。我们选择当下卷积神经网络YOLOv5来进行火焰识别检测。6月9日,Ultralytics公司开源了YOL…...

【Python入门】Python循环语句(while循环的基础语法)
前言 📕作者简介:热爱跑步的恒川,致力于C/C、Java、Python等多编程语言,热爱跑步,喜爱音乐的一位博主。 📗本文收录于Python零基础入门系列,本专栏主要内容为Python基础语法、判断、循环语句、函…...

JS中 Math 和 Number 内置对象常用的一些方法
JS中 Math 和 Number 内置对象常用的一些方法 Math.abs(num)Math.ceil(num)Math.floor(num)Math.max(num1, num2, ... , numN)Math.min(num1, num2, ... , numN)Math.pow(base, exponent)Math.random()Math.round(num)Math.sqrt(num)Number.toFixed(digits)Number.toString(rad…...
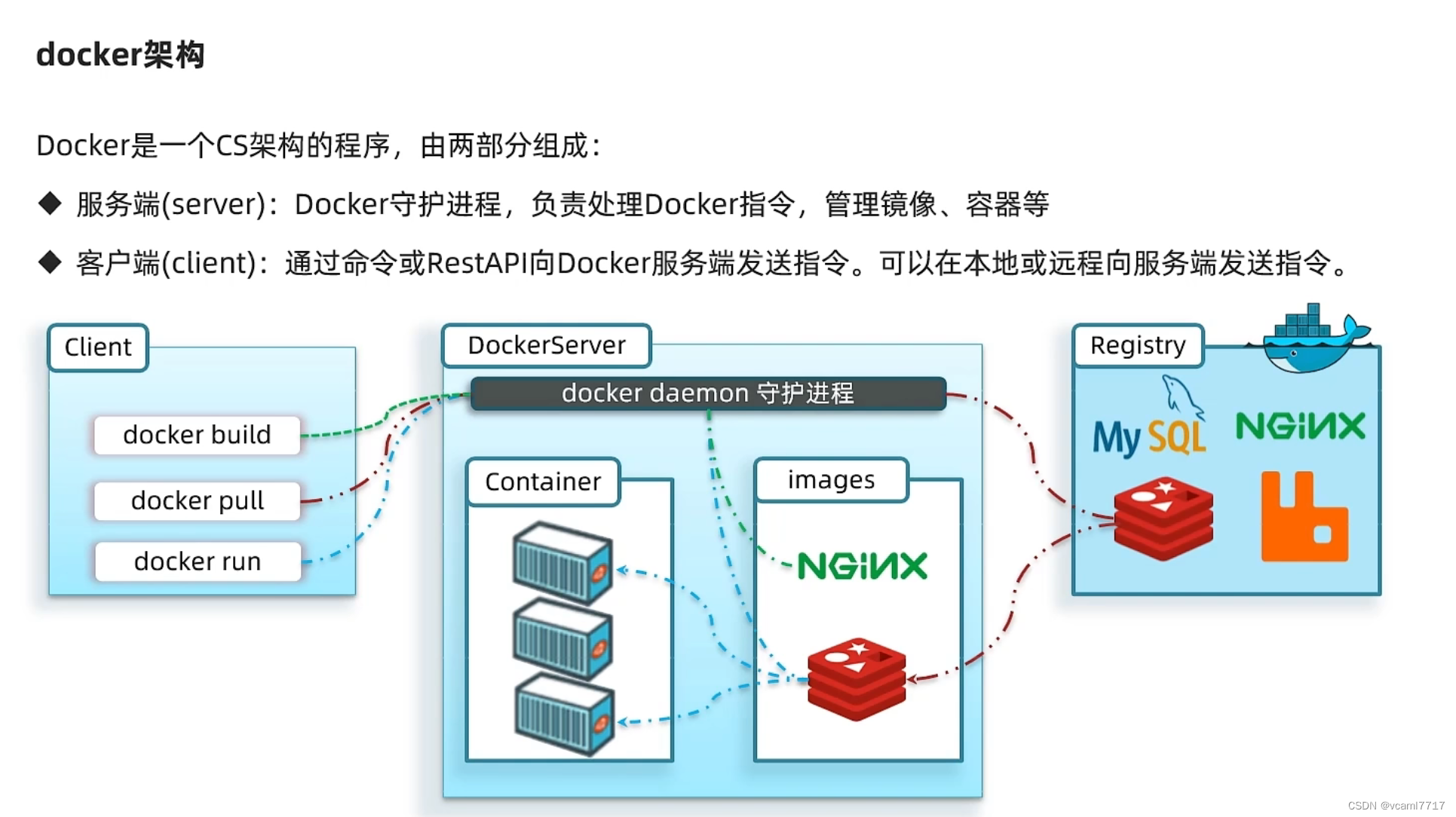
Docker的使用 (1.什么是docker)
前言 这个系列是我自己学习使用docker的记录和分享,作为一名开发人员,你需要了解这个东西并且学会它的简单使用,但是作为一名开发而不是运维,不要花过多的时间去深究它的原理,而是把它当作一个工具即可 docker Docke…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
