使用底层代码(无框架)实现卷积神经网络理解CNN逻辑
首先将数据集放入和底下代码同一目录中,然后导入一些相关函数的文件cnn_utils.py:
import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.python.framework import ops
def load_dataset():train_dataset = h5py.File('datasets/train_signs.h5', "r")train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set featurestrain_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labelstest_dataset = h5py.File('datasets/test_signs.h5', "r")test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set featurestest_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labelsclasses = np.array(test_dataset["list_classes"][:]) # the list of classestrain_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):"""Creates a list of random minibatches from (X, Y)Arguments:X -- input data, of shape (input size, number of examples) (m, Hi, Wi, Ci)Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples) (m, n_y)mini_batch_size - size of the mini-batches, integerseed -- this is only for the purpose of grading, so that you're "random minibatches are the same as ours.Returns:mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)"""m = X.shape[0] # number of training examplesmini_batches = []np.random.seed(seed)# Step 1: Shuffle (X, Y)permutation = list(np.random.permutation(m))shuffled_X = X[permutation,:,:,:]shuffled_Y = Y[permutation,:]# Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionningfor k in range(0, num_complete_minibatches):mini_batch_X = shuffled_X[k * mini_batch_size : k * mini_batch_size + mini_batch_size,:,:,:]mini_batch_Y = shuffled_Y[k * mini_batch_size : k * mini_batch_size + mini_batch_size,:]mini_batch = (mini_batch_X, mini_batch_Y)mini_batches.append(mini_batch)# Handling the end case (last mini-batch < mini_batch_size)if m % mini_batch_size != 0:mini_batch_X = shuffled_X[num_complete_minibatches * mini_batch_size : m,:,:,:]mini_batch_Y = shuffled_Y[num_complete_minibatches * mini_batch_size : m,:]mini_batch = (mini_batch_X, mini_batch_Y)mini_batches.append(mini_batch)return mini_batches
def convert_to_one_hot(Y, C):Y = np.eye(C)[Y.reshape(-1)].Treturn Y
def forward_propagation_for_predict(X, parameters):"""Implements the forward propagation for the model: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SOFTMAXArguments:X -- input dataset placeholder, of shape (input size, number of examples)parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3"the shapes are given in initialize_parametersReturns:Z3 -- the output of the last LINEAR unit"""# Retrieve the parameters from the dictionary "parameters" W1 = parameters['W1']b1 = parameters['b1']W2 = parameters['W2']b2 = parameters['b2']W3 = parameters['W3']b3 = parameters['b3'] # Numpy Equivalents:Z1 = tf.add(tf.matmul(W1, X), b1) # Z1 = np.dot(W1, X) + b1A1 = tf.nn.relu(Z1) # A1 = relu(Z1)Z2 = tf.add(tf.matmul(W2, A1), b2) # Z2 = np.dot(W2, a1) + b2A2 = tf.nn.relu(Z2) # A2 = relu(Z2)Z3 = tf.add(tf.matmul(W3, A2), b3) # Z3 = np.dot(W3,Z2) + b3return Z3
def predict(X, parameters):W1 = tf.convert_to_tensor(parameters["W1"])b1 = tf.convert_to_tensor(parameters["b1"])W2 = tf.convert_to_tensor(parameters["W2"])b2 = tf.convert_to_tensor(parameters["b2"])W3 = tf.convert_to_tensor(parameters["W3"])b3 = tf.convert_to_tensor(parameters["b3"])params = {"W1": W1,"b1": b1,"W2": W2,"b2": b2,"W3": W3,"b3": b3}x = tf.placeholder("float", [12288, 1])z3 = forward_propagation_for_predict(x, params)p = tf.argmax(z3)sess = tf.Session()prediction = sess.run(p, feed_dict = {x: X})return prediction
padding
卷积网络通常会出现两大问题:
- 图像缩小问题。正常卷积后会缩小高度和宽度,特别如果是深层的CNN,这样的问题会影响网络性能。
- 边缘信息丢失,因为边缘的值被卷积核卷积的次数较。
而padding可以很好的解决这两个问题。
首先实现padding填充的代码:
def zero_pad(X, pad):"""把数据集X的图像边界全部使用0来扩充pad个宽度和高度。参数:X - 图像数据集,维度为(样本数,图像高度,图像宽度,图像通道数)pad - 整数,每个图像在垂直和水平维度上的填充量返回:X_paded - 扩充后的图像数据集,维度为(样本数,图像高度 + 2*pad,图像宽度 + 2*pad,图像通道数)"""X_paded = np.pad(X, ((0, 0), # 样本数,不填充(pad, pad), # 图像高度,你可以视为上面填充x个,下面填充y个(x,y)(pad, pad), # 图像宽度,你可以视为左边填充x个,右边填充y个(x,y)(0, 0)), # 通道数,不填充'constant', constant_values=0) # 连续一样的值填充return X_paded
可以测试代码看padding后的效果:
np.random.seed(1)
x = np.random.randn(4, 3, 3, 2)
x_paded = zero_pad(x, 2)
# 查看信息
print("x.shape =", x.shape)
print("x_paded.shape =", x_paded.shape)
print("x[1, 1] =", x[1, 1])
print("x_paded[1, 1] =", x_paded[1, 1])# 绘制图
fig, axarr = plt.subplots(1, 2) # 一行两列
axarr[0].set_title('x')
axarr[0].imshow(x[0, :, :, 0])
axarr[1].set_title('x_paded')
axarr[1].imshow(x_paded[0, :, :, 0])
plt.show()
输出:
x.shape = (4, 3, 3, 2)
x_paded.shape = (4, 7, 7, 2)
x[1, 1] = [[ 0.90085595 -0.68372786][-0.12289023 -0.93576943][-0.26788808 0.53035547]]
x_paded[1, 1] = [[0. 0.][0. 0.][0. 0.][0. 0.][0. 0.][0. 0.][0. 0.]]

Conv
前向传播
单个卷积核的卷积过程如图(2D),3D则是相同通道的卷积核的每个通道与输入对应通道的进行2D的卷积然后相加,3D卷积的输出的通道数=卷积核的个数。

n × n × n c − − C o n v ( f × f × n c , n 1 c 个 , s t r i d e , p a d d i n g ) − − > m × m × n 1 c n×n×n_c--Conv(f×f×n_c,n1_c个, stride, padding)-->m×m×n1_c n×n×nc−−Conv(f×f×nc,n1c个,stride,padding)−−>m×m×n1c
m = ⌊ n − f + 2 × p a d d i n g s t r i d e ⌋ + 1 m = ⌊ \frac{n − f + 2 × p a dding }{ st r i d e }⌋ + 1 m=⌊striden−f+2×padding⌋+1
若除以步幅不为整数时要向下取整。
因为卷积核的个数决定输出的通道数,第l层的卷积核通道数=第l-1层的输出(即l层的输入)的通道数,第l层的卷积核的个数=第l+1层的输入(即第l层的输出)的通道数,所以l层的卷积核(大小×通道数×个数)为:
f × f × n c l − 1 × n c l f×f×n^{l-1}_c×n^{l}_c f×f×ncl−1×ncl
n c l − 1 为 l − 1 层的卷积核个数, n c l 为 l 层的卷积核个数 n^{l-1}_c为l-1层的卷积核个数,n^{l}_c为l层的卷积核个数 ncl−1为l−1层的卷积核个数,ncl为l层的卷积核个数
# 单个卷积操作
def conv_single_step(a_slice_prev, W, b):"""在前一层的激活输出的一个片段上应用一个由参数W定义的过滤器。这里切片大小和过滤器大小相同参数:a_slice_prev - 输入数据的一个片段,维度为(过滤器大小,过滤器大小,上一通道数)W - 权重参数,包含在了一个矩阵中,维度为(过滤器大小,过滤器大小,上一通道数)b - 偏置参数,包含在了一个矩阵中,维度为(1,1,1)返回:Z - 在输入数据的片X上卷积滑动窗口(w,b)的结果。"""s = np.multiply(a_slice_prev, W) + bZ = np.sum(s)return Zdef conv_forward(A_prev, W, b, hparameters):"""实现卷积函数的前向传播参数:A_prev - 上一层的激活输出矩阵,维度为(m, n_H_prev, n_W_prev, n_C_prev),(样本数量,上一层图像的高度,上一层图像的宽度,上一层过滤器数量)W - 权重矩阵,维度为(f, f, n_C_prev, n_C),(过滤器大小,过滤器大小,上一层的过滤器数量,这一层的过滤器数量)b - 偏置矩阵,维度为(1, 1, 1, n_C),(1,1,1,这一层的过滤器数量)hparameters - 包含了"stride"与 "pad"的超参数字典。返回:Z - 卷积输出,维度为(m, n_H, n_W, n_C),(样本数,图像的高度,图像的宽度,过滤器数量)cache - 缓存了一些反向传播函数conv_backward()需要的一些数据"""# 获取来自上一层数据的基本信息(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape# 获取权重矩阵的基本信息(f, f, n_C_prev, n_C) = W.shape# 获取超参数hparameters的值stride = hparameters["stride"]pad = hparameters["pad"]# 计算卷积后的图像的宽度高度,参考上面的公式,使用int()来进行板除n_H = int((n_H_prev - f + 2 * pad) / stride) + 1n_W = int((n_W_prev - f + 2 * pad) / stride) + 1# 使用0来初始化卷积输出ZZ = np.zeros((m, n_H, n_W, n_C))# 通过A_prev创建填充过了的A_prev_padA_prev_pad = zero_pad(A_prev, pad)for i in range(m): # 遍历样本a_prev_pad = A_prev_pad[i] # 选择第i个样本的扩充后的激活矩阵for h in range(n_H): # 在输出的垂直轴上循环for w in range(n_W): # 在输出的水平轴上循环for c in range(n_C): # 循环遍历输出的通道# 定位当前的切片位置vert_start = h * stride # 竖向,开始的位置vert_end = vert_start + f # 竖向,结束的位置horiz_start = w * stride # 横向,开始的位置horiz_end = horiz_start + f # 横向,结束的位置# 切片位置定位好了我们就把它取出来,需要注意的是我们是“穿透”取每层通道的(3D层面)# 自行脑补一下吸管插入一层层的橡皮泥就明白了a_slice_prev = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]# 执行单步卷积,遍历到的切片与第c个卷积核进行单卷集操作,得到输出的第c层的对应的一个值Z[i, h, w, c] = conv_single_step(a_slice_prev, W[:, :, :, c], b[0, 0, 0, c])# 数据处理完毕,验证数据格式是否正确assert (Z.shape == (m, n_H, n_W, n_C))# 存储一些缓存值,以便于反向传播使用cache = (A_prev, W, b, hparameters)return (Z, cache)'''
卷积层的最后应该要进行激活的,activation可以是sigmoid、relu、tanh等,但这里我们就不这么做了,
只是用无框架代码解释其底层逻辑
A[i, h, w, c] = activation(Z[i, h, w, c])
'''
这里遍历切片的位置定义可参考下图:

测试代码:
np.random.seed(1)A_prev = np.random.randn(10, 4, 4, 3)
W = np.random.randn(2, 2, 3, 8)
b = np.random.randn(1, 1, 1, 8)hparameters = {"pad": 2, "stride": 1}Z, cache_conv = conv_forward(A_prev, W, b, hparameters)print("np.mean(Z) = ", np.mean(Z))
print("A_prev.shape =", cache_conv[0].shape)
print("W.shape =", cache_conv[1].shape)
print("b.shape =", cache_conv[2].shape)
输出:
np.mean(Z) = 0.15585932488906465
A_prev.shape = (10, 4, 4, 3)
W.shape = (2, 2, 3, 8)
b.shape = (1, 1, 1, 8)
可以看到输入、卷积核及偏差的shape与测试代码中的一致。
反向传播
若是使用DL框架,只需要写出前向传播框架就会自动计算出反向传播的梯度值。
首先列出反向传播所需要的计算公式:
- 计算dA的:
d A + = ∑ h = 0 n H ∑ w = 0 n W W c × d Z h w (1) dA += \sum ^{n_H} _{h=0} \sum ^{n_W} _{w=0} W_{c} \times dZ_{hw} \tag{1} dA+=h=0∑nHw=0∑nWWc×dZhw(1)
其中 W c W_c Wc是过滤器, Z h w Z_{hw} Zhw是一个标量,是卷积层第h行第w列的使用点乘计算后的输出Z的梯度(即输出Z的每个切片对应的梯度)。
需要注意的是在每次更新dA的时候,都会用第c个过滤器 W c W_c Wc乘以对应的第c层通道的dZ,因为在前向传播的时候,每个过滤器都与a_slice进行了点乘相加得到某一层通道的一个值(即输入的每一块切片都是用不同的卷积核卷积过,第c个卷积核与其卷积得到第c层通道的一个值),所以在计算dA的每一块的切片的梯度的时候,我们是计算每个卷积核与对应层的dZ的反向操作的结果之和。公式可以如下表示:
da_perv_pad[vert_start:vert_end,horiz_start:horiz_end,:] += W[:,:,:,c] * dZ[i,h,w,c]

如图(网图加上自己的画笔)是一个单个卷积操作的正向过程,可以看到是一个卷积核对一个切片(3D)进行卷积是得到了某一层的一个值(2D)(图中的红蓝框);而反向计算我们也按这个顺序反向,每个卷积核与dZ对应层(通道)的一个值(2D)相乘然后每个结果相加,就得到对应切片的范围的dA(3D)。大概更直观的过程就是:
正向过程: 3 D ∗ 卷积核 − − > 2 D 正向过程:3D * 卷积核 --> 2D 正向过程:3D∗卷积核−−>2D
反向过程: 2 D ∗ 卷积核 − − > 3 D 反向过程:2D * 卷积核 --> 3D 反向过程:2D∗卷积核−−>3D
- 计算dW的:
d W c + = ∑ h = 0 n H ∑ w = 0 n W a s l i c e × d Z h w (2) dW_c += \sum^{n_H}_{h=0} \sum^{n_W}_{w=0}a_{slice} \times dZ_{hw} \tag{2} dWc+=h=0∑nHw=0∑nWaslice×dZhw(2)
其中, a s l i c e a_{slice} aslice 对应着 Z i j Z_{ij} Zij的激活值。由此,我们就可以推导W的梯度,因为我们使用了卷积核来对数据进行窗口滑动,在这里,我们实际上是切出了和过滤器一样大小的切片,切了多少次就产生了多少个梯度,所以我们需要把它们加起来得到这个数据集的整体dW。用公式概括:
dW[:,:,:, c] += a_slice * dZ[i , h , w , c]
同样可以参考上面的dA求解过程即配图。单步卷积的正向是一个切片与一个卷积核卷积得到一层的一个值,而输入的每个切片都是用到这个卷积核(但一个卷积层有一个或多个卷积核),所以反向操作是每个卷积核的梯度是所有切片与某一层通道(这个卷积核卷积后得到的对应层)的所有值一一对应相乘后相加。大概更直观的过程就是:
正向过程:卷积核 1 − − > 输出结果的第 1 层通道,卷积核 2 − − > 输出结果的第 2 层通道 正向过程:卷积核1-->输出结果的第1层通道,卷积核2-->输出结果的第2层通道 正向过程:卷积核1−−>输出结果的第1层通道,卷积核2−−>输出结果的第2层通道
反向过程:输出结果的第 1 层通道 − − > 卷积核 1 ,输出结果的第 2 层通道 − − > 卷积核 2 反向过程:输出结果的第1层通道-->卷积核1,输出结果的第2层通道-->卷积核2 反向过程:输出结果的第1层通道−−>卷积核1,输出结果的第2层通道−−>卷积核2
- 计算db的:
每个卷积核只对应一个b的值,所以b的梯度比较好计算:
d b = ∑ h ∑ w d Z h w (3) db = \sum^{}_{h} \sum^{}_{w}dZ_{hw} \tag{3} db=h∑w∑dZhw(3)
可以用一行代码进行概括:
db[:,:,:,c] += dZ[ i, h, w, c]
因为一个卷积核对应一个b,输出结果的每一层对应的是一个卷积核,所以输出结果的每一层对应的是一个b。
接下来用这3个公式求卷积的反向过程:
def conv_backward(dZ, cache):"""实现卷积层的反向传播参数:dZ - 卷积层的输出Z的 梯度,维度为(m, n_H, n_W, n_C) 取决于使用的是什么激活函数cache - 反向传播所需要的参数,conv_forward()的输出之一返回:dA_prev - 卷积层的输入(A_prev)的梯度值,维度为(m, n_H_prev, n_W_prev, n_C_prev)dW - 卷积层的权值的梯度,维度为(f,f,n_C_prev,n_C)db - 卷积层的偏置的梯度,维度为(1,1,1,n_C)"""# 获取cache的值(A_prev, W, b, hparameters) = cache# 获取A_prev的基本信息(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape# 获取dZ的基本信息(m, n_H, n_W, n_C) = dZ.shape# 获取权值的基本信息(f, f, n_C_prev, n_C) = W.shape# 获取hparaeters的值pad = hparameters["pad"]stride = hparameters["stride"]# 初始化各个梯度的结构dA_prev = np.zeros((m, n_H_prev, n_W_prev, n_C_prev))dW = np.zeros((f, f, n_C_prev, n_C))db = np.zeros((1, 1, 1, n_C))# 前向传播中我们使用了pad,反向传播也需要使用,这是为了保证数据结构一致A_prev_pad = zero_pad(A_prev, pad)dA_prev_pad = zero_pad(dA_prev, pad)# 现在处理数据for i in range(m):# 选择第i个扩充了的数据的样本,降了一维。a_prev_pad = A_prev_pad[i]da_prev_pad = dA_prev_pad[i]for h in range(n_H):for w in range(n_W):for c in range(n_C):# 定位切片位置vert_start = hvert_end = vert_start + fhoriz_start = whoriz_end = horiz_start + f# 定位完毕,开始切片a_slice = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]# 切片完毕,使用上面的公式计算梯度,第c个卷积核与dZ的第c层通道反向计算得到对应的3D切片da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:, :, :, c] * dZ[i, h, w, c]dW[:, :, :, c] += a_slice * dZ[i, h, w, c]db[:, :, :, c] += dZ[i, h, w, c]# 设置第i个样本最终的dA_prev,即把非填充的数据取出来。dA_prev的shape要和A_prev的保持一致才是正确的,下面assert验证dA_prev[i, :, :, :] = da_prev_pad[pad:-pad, pad:-pad, :]# 数据处理完毕,验证数据格式是否正确assert (dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))return (dA_prev, dW, db)
测试上面的代码:
np.random.seed(1)
# 初始化参数
A_prev = np.random.randn(10, 4, 4, 3)
W = np.random.randn(2, 2, 3, 8)
b = np.random.randn(1, 1, 1, 8)
hparameters = {"pad": 2, "stride": 1}# 前向传播
Z, cache_conv = conv_forward(A_prev, W, b, hparameters)
# 反向传播
dA, dW, db = conv_backward(Z, cache_conv)
print("dA.shape =", dA.shape)
print("dW.shape =", dW.shape)
print("db.shape =", db.shape)
输出:
dA.shape = (10, 4, 4, 3)
dW.shape = (2, 2, 3, 8)
db.shape = (1, 1, 1, 8)
可以看到输入的dA、卷积核的dW及偏差的db的shape都与之相对应,从正向传播的输出输入到反向传播过程中而产生的结果无误。
pooling
正向传播
池化层可以减小图像的宽高(通道数不变),池化核对每层分别进行池化操作。池化层是CNN的静态属性,没有参数进行学习更新,只需要设置超参即可(size、stride、pooling等)。
池化层可以缩减模型大小,提高计算速度;提高提取特征的鲁棒性。
池化分为最大值池化和均值池化:
- max pooling:取池化核区域内的最大值
- 项目2取池化核区域内的平均值


池化操作后的高宽的计算跟卷积一样,不同的是输出的通道数不变:
n c l = n c l − 1 n^l_c = n^{l-1}_c ncl=ncl−1
def pool_forward(A_prev, hparameters, mode="max"):"""实现池化层的前向传播参数:A_prev - 输入数据,维度为(m, n_H_prev, n_W_prev, n_C_prev)hparameters - 包含了 "f" 和 "stride"的超参数字典mode - 模式选择【"max" | "average"】返回:A - 池化层的输出,维度为 (m, n_H, n_W, n_C)cache - 存储了一些反向传播需要用到的值,包含了输入和超参数的字典。"""# 获取输入数据的基本信息(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape# 获取超参数的信息f = hparameters["f"]stride = hparameters["stride"]# 计算输出维度n_H = int((n_H_prev - f) / stride) + 1n_W = int((n_W_prev - f) / stride) + 1n_C = n_C_prev# 初始化输出矩阵A = np.zeros((m, n_H, n_W, n_C))for i in range(m): # 遍历样本for h in range(n_H): # 在输出的垂直轴上循环for w in range(n_W): # 在输出的水平轴上循环for c in range(n_C): # 循环遍历输出的通道# 定位当前的切片位置vert_start = h * stride # 竖向,开始的位置vert_end = vert_start + f # 竖向,结束的位置horiz_start = w * stride # 横向,开始的位置horiz_end = horiz_start + f # 横向,结束的位置# 遍历到的区域切片,这里是对c层通道进行切片(2D层面)a_slice_prev = A_prev[i, vert_start:vert_end, horiz_start:horiz_end, c]# 对切片进行池化操作,对遍历到的第c层的区域进行池化操作if mode == "max":A[i, h, w, c] = np.max(a_slice_prev)elif mode == "average":A[i, h, w, c] = np.mean(a_slice_prev)# 池化完毕,校验数据格式assert (A.shape == (m, n_H, n_W, n_C))# 校验完毕,开始存储用于反向传播的值cache = (A_prev, hparameters)return A, cache
测试代码:
np.random.seed(1)
A_prev = np.random.randn(2, 4, 4, 3)
hparameters = {"f": 4, "stride": 1}A, cache = pool_forward(A_prev, hparameters, mode="max")
print("mode = max")
print("A =", A)
print("----------------------------")
A, cache = pool_forward(A_prev, hparameters, mode="average")
print("mode = average")
print("A =", A)
输出结果:
mode = max
A = [[[[1.74481176 1.6924546 2.10025514]]][[[1.19891788 1.51981682 2.18557541]]]]
----------------------------
mode = average
A = [[[[-0.09498456 0.11180064 -0.14263511]]][[[-0.09525108 0.28325018 0.33035185]]]]
4×4×3的输入经过stride为1的4×4的池化之后输出为1×1×3,样本数为2,输出的shape为(2, 1, 1, 3),没有错误。
反向传播
即使池化层没有反向传播过程中要更新的参数,我们仍然需要通过池化层反向传播梯度,以便为在池化层之前的层(比如卷积层)计算梯度。
- max pooling的反向传播:
创建一个create_mask_from_window()的函数,用来记池化核区域的最大值的位置。因为正向的操作是取输入的池化核区域内的最大值一个值,而反向操作是还是取这个输入,在对应的池化核区域内只保留最大值的值其余置0,所以我们先记录最大值位置的矩阵通过相乘来达到我们的目的。
X = [ 1 3 4 2 ] → M = [ 0 0 1 0 ] X = \begin{bmatrix} 1 && 3 \\ 4 && 2 \end {bmatrix} \quad \rightarrow \quad M = \begin{bmatrix} 0 && 0 \\ 1 && 0 \end {bmatrix} X=[1432]→M=[0100]
正向传播首先是经过卷积层,然后滑动地取卷积层最大值构成了池化层,要记录最大值的位置,才能反向传播到卷积层。
def create_mask_from_window(x):"""从输入矩阵中创建掩码,以保存最大值的矩阵的位置。参数:x - 一个维度为(f,f)的矩阵返回:mask - 包含x的最大值的位置的矩阵"""mask = x == np.max(x)return mask
测试一下代码,看输出结果:
np.random.seed(1)x = np.random.randn(2, 3)mask = create_mask_from_window(x)print("x = " + str(x))
print("mask = " + str(mask))
输出:
x = [[ 1.62434536 -0.61175641 -0.52817175][-1.07296862 0.86540763 -2.3015387 ]]
mask = [[ True False False][False False False]]
是以布尔值为矩阵来记录最大值的位置。
- average pooling的反向传播:
而均值池化的正向操作是取池化核内的平均值得到一个值,所以反向操作就根据后一层的梯度的其中一个值来得到对应区域内的所有平均值。
d Z = 1 → d Z = [ 1 4 1 4 1 4 1 4 ] dZ=1 \quad \rightarrow \quad dZ = \begin{bmatrix} \frac{1}{4} & \frac{1}{4} \\ \frac{1}{4} & \frac{1}{4} \\ \end{bmatrix} dZ=1→dZ=[41414141]
def distribute_value(dz, shape):"""给定一个值,为按矩阵大小平均分配到每一个矩阵位置中。参数:dz - 输入的实数shape - 元组,两个值,分别为n_H , n_W返回:a - 已经分配好了值的矩阵,里面的值全部一样。"""# 获取矩阵的大小(n_H, n_W) = shape# 计算平均值average = dz / (n_H * n_W)# 填充入矩阵a = np.ones(shape) * averagereturn a
测试:
dz = 2
shape = (2, 2)a = distribute_value(dz, shape)
print("a = " + str(a))
输出:
a = [[0.5 0.5][0.5 0.5]]
可以看到2平均分为2×2=4份平均值为0.5验正确。
池化层的反向操作的实现:
def pool_backward(dA, cache, mode="max"):"""实现池化层的反向传播参数:dA - 池化层的输出的梯度,和池化层的输出的维度一样cache - 池化层前向传播时所存储的参数。mode - 模式选择,【"max" | "average"】返回:dA_prev - 池化层的输入的梯度,和A_prev的维度相同"""# 获取cache中的值(A_prev, hparaeters) = cache# 获取hparaeters的值f = hparaeters["f"]stride = hparaeters["stride"]# 获取A_prev和dA的基本信息(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape(m, n_H, n_W, n_C) = dA.shape# 初始化输出的结构dA_prev = np.zeros_like(A_prev)# 开始处理数据for i in range(m):a_prev = A_prev[i]for h in range(n_H):for w in range(n_W):for c in range(n_C):# 定位切片位置vert_start = hvert_end = vert_start + fhoriz_start = whoriz_end = horiz_start + f# 选择反向传播的计算方式if mode == "max":# 开始切片a_prev_slice = a_prev[vert_start:vert_end, horiz_start:horiz_end, c]# 创建掩码mask = create_mask_from_window(a_prev_slice)# 计算dA_prev,一层一层对应的反操作dA_prev[i, vert_start:vert_end, horiz_start:horiz_end, c] += np.multiply(mask, dA[i, h, w, c])elif mode == "average":# 获取dA的值da = dA[i, h, w, c]# 定义过滤器大小shape = (f, f)# 平均分配dA_prev[i, vert_start:vert_end, horiz_start:horiz_end, c] += distribute_value(da, shape)# 数据处理完毕,开始验证格式assert (dA_prev.shape == A_prev.shape)return dA_prev
测试一下代码:
np.random.seed(1)
A_prev = np.random.randn(5, 5, 3, 2)
hparameters = {"stride": 1, "f": 2}
A, cache = pool_forward(A_prev, hparameters)
dA = np.random.randn(5, 4, 2, 2)dA_prev = pool_backward(dA, cache, mode="max")
print("mode = max")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1, 1])
print()
dA_prev = pool_backward(dA, cache, mode="average")
print("mode = average")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1, 1])
输出:
mode = max
mean of dA = 0.14571390272918056
dA_prev[1,1] = [[ 0. 0. ][ 5.05844394 -1.68282702][ 0. 0. ]]mode = average
mean of dA = 0.14571390272918056
dA_prev[1,1] = [[ 0.08485462 0.2787552 ][ 1.26461098 -0.25749373][ 1.17975636 -0.53624893]]
无报错证明通过了assert验证,dA_prev[1, 1]输出的是第二个样本的第二行的切片,因为宽度为3,通道数为2,所以输出了个shape为(3, 2)的矩阵也没问题。
因为池化是对每一层分别池化进行池化操作(不改变通道数的操作),所以反操作也是一层一层对应的反操作。
相关文章:

使用底层代码(无框架)实现卷积神经网络理解CNN逻辑
首先将数据集放入和底下代码同一目录中,然后导入一些相关函数的文件cnn_utils.py: import math import numpy as np import h5py import matplotlib.pyplot as plt import tensorflow as tf from tensorflow.python.framework import ops def load_data…...
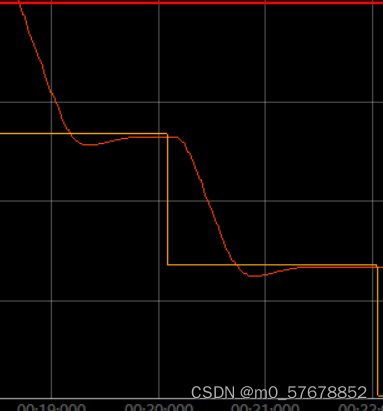
PID单环控制(位置环)
今天我们来聊一聊pid如何控制轮子转动位置 前期准备调试过程 前期准备 需要准备的几个条件: 1.获取实时编码器的计数值 2.写好pid控制算法的函数 3.设定好时间多久执行一次pid计算,并设置限幅输出。 4.多久执行一次pid输出 接下来我们看看这几个部分的…...
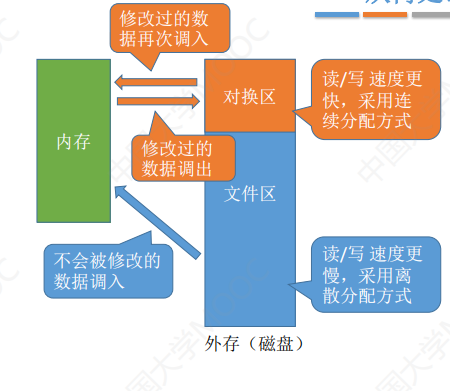
内存基础知识
概述 内存可存放数据。程序执行前需要先将外存中的数据放到内存中才能被CPU处理,因为CPU处理速度过快,而从硬盘读取数据较慢,所以内存是为了缓和CPU和硬盘之间的读取速度矛盾 在多道程序环境下,系统中会有多个程序并发执行&…...

快速入门matlab——运算方法
这是一个matlab神经网络的简单应用,主要用于预测光伏出力,输入为温度湿度等因素,输出为光伏出力 基于Matlab和CPLEX的2变量机组组合调度程序 基于MATLABCPLEX 的机组最优组合,成功求解表格化,图示化的机组组合结果 …...
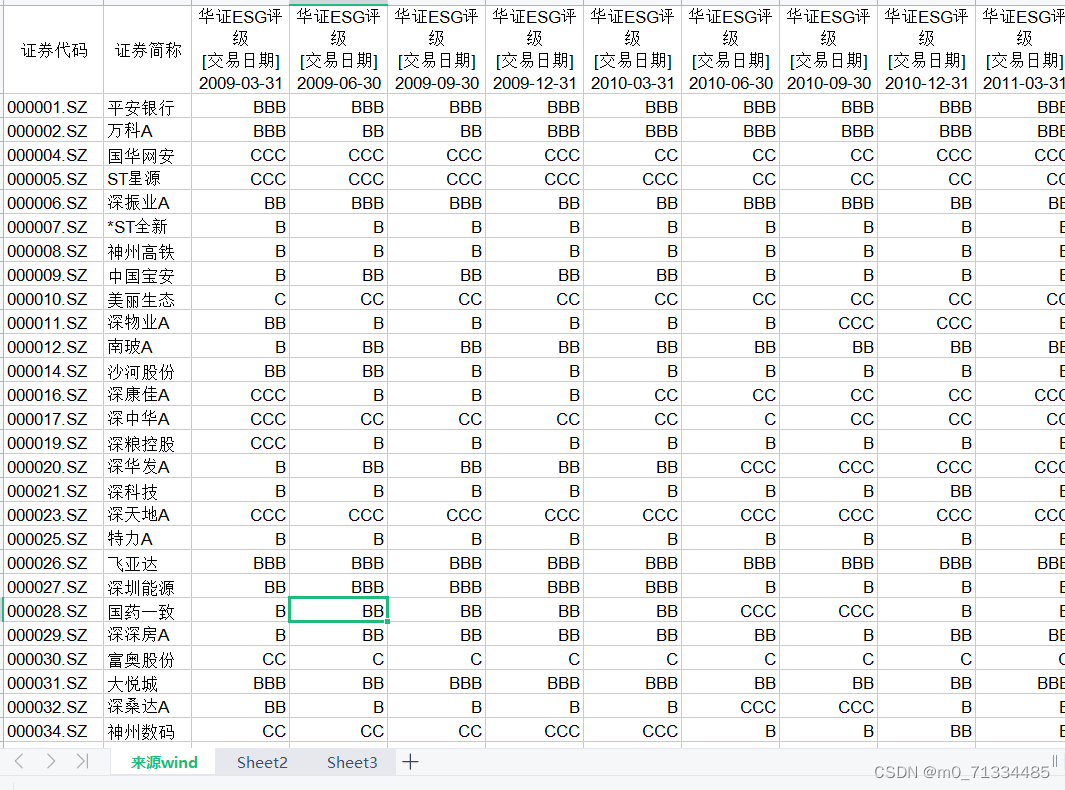
2009.03-2022.06华证ESG季度评级(季度)
2009.03-2022.06华证ESG评级(季度) 1、时间:2009.03-2022.06.15 2、来源:整理自Wind 3、指标:华证ESG(只有综合评级,无细分评级数据) 4、样本数量:A股4800多家公司 …...
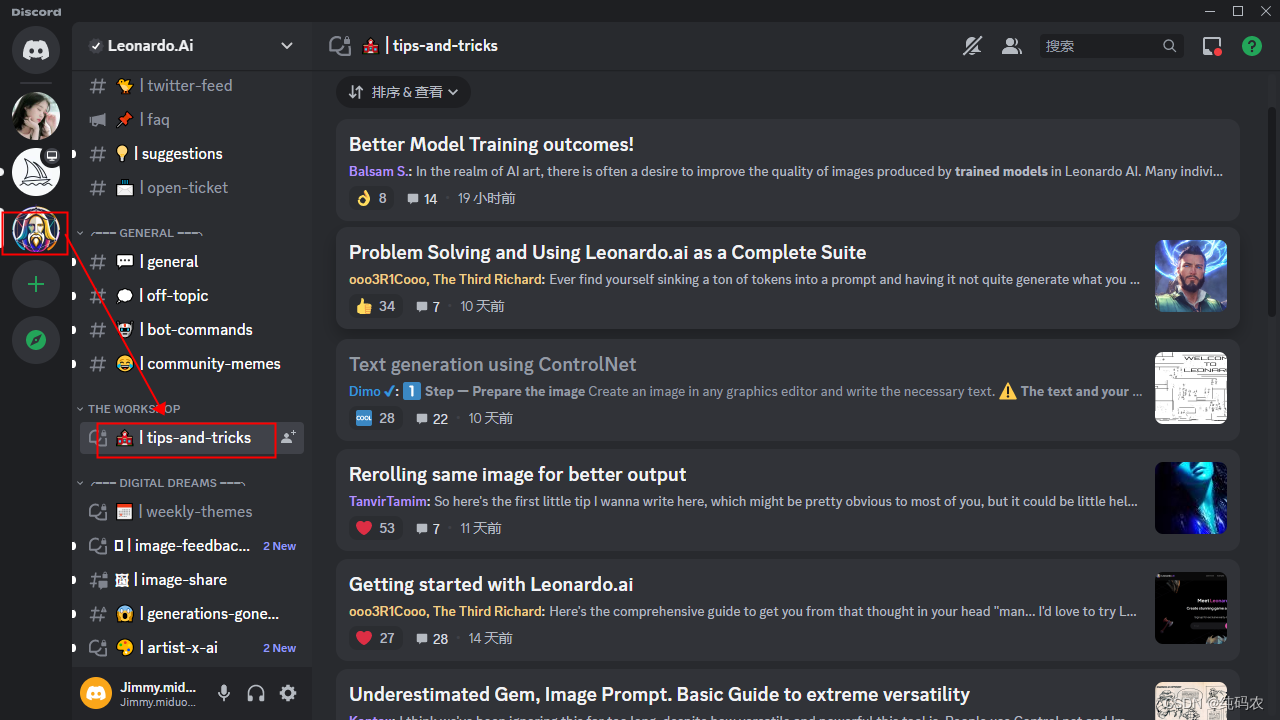
【大数据模型】LeonardoAi让心中所想跃然纸上
汝之观览,吾之幸也! 本文主要聊聊LeonardoAi绘图工具 一、注册Discord账号 不管LeonardoAi还是midjourney,都需要注册一个Discord账号,Discord是一个社区软件,在这里可以进行讨论和交流使用心得 LeonardoAi官网地址 …...

如何区别BI、大数据、信息化和数字化转型
商业智能BI可以实现业务流程和业务数据的规范化、流程化、标准化,打通ERP、OA、CRM等不同业务信息系统,整合归纳企业数据,利用数据可视化满足企业不同人群对数据查询、分析和探索的需求,从而为管理和业务提供数据依据和决策支持。…...

ESP32-C2开发板Homekit例程
准备 1.1硬件ESP32 C2开发板,如图1-1所示 图1-1 ESP32 C2开发板 1.2软件 CozyLife APP可以在各大应用市场搜索下载,也可以扫描二维码下载如图1-2所示 HomeKit flash download tool 烧录工具 esp32c2 homkit演示固件 烧录教程 打开flash_download_to…...
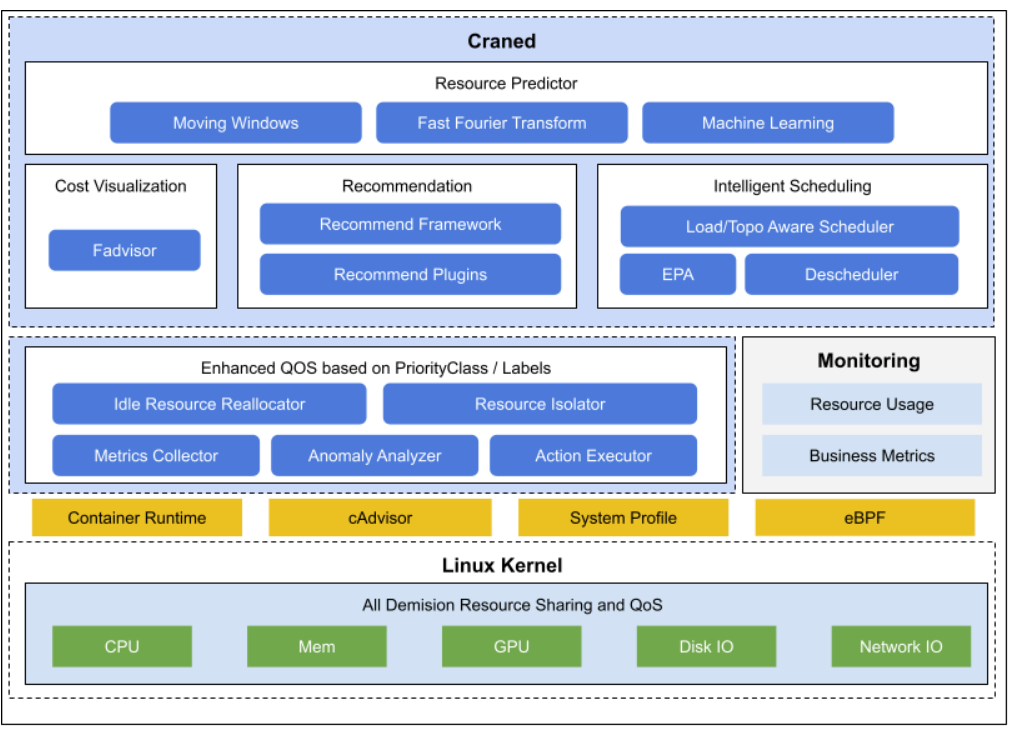
快速搭建一个 Kubernetes+Crane 环境,以及如何基于 Crane 优化你的集群和应用初体验
文章目录 一、活动介绍二、环境搭建三、安装本地的 Kind 集群和 Crane 组件四、界面截图五、主要功能六、整体架构七、Crane的优势八、总结参考文献 一、活动介绍 Crane 是由腾讯云主导开源的国内第一个基于云原生技术的成本优化项目,遵循 FinOps 标准,…...

深度学习图像识别模型:递归神经网络
深度学习是一种人工智能技术,它用于解决各种问题,包括自然语言处理、计算机视觉等。递归神经网络(Recurrent Neural Network,RNN)是深度学习中的一种神经网络模型,主要用于处理序列数据,例如文本…...

上门家教预约小程序开发 良师就在你身边
社会的发展科技的进步让人们对教育的重视度也逐渐升高,很多家长可以说是为了孩子的教育操碎了心。在学校还好有老师辅导,节假日在家的时候,很多家长自己本身文化知识有限或者工作繁忙没有时间辅导,送去辅导班来回接送又很麻烦&…...

CMake Practice 学习笔记五--cmake常用变量
这里列举一些cmake常用变量,后面带**表示常用,了解下,不用全部记住。 1、CMAKE_BINARY_DIR PROJECT_BINARY_DIR ** <projectname>_BINARY_DIR 这三个变量指代的内容是一样的,如果是 in source 编译,指的就是工程顶层目…...

Facebook 广告效果越来越差,怎么办?
在如今的数字营销领域中,Facebook作为独立站卖家首选的推广引流平台,具备了许多优势。 一方面,Facebook拥有庞大的用户数量,是全球最大的社交媒体平台之一。另一方面,Facebook的广告算法可以将广告推送给更加精准的受…...
)
Netty核心组件模块(三)
1.Netty心跳检测机制 1>.编写网络应用的时候,客户端和服务器端需要通过心跳检测机制来判断对方是否还存活,如果发生了异常,那么需要进行相应的处理; 1.1.案例–编程实现Netty的心跳检测机制 1.1.1.需求 ①.当服务器超过3秒没有读时,就提示读空闲; ②.当服务器超过5秒没有…...
k8s 集群搭建详细教程
参考: Kubernetes 文档 / 入门 / 生产环境 / 使用部署工具安装 Kubernetes / 使用 kubeadm 引导集群 / 安装 kubeadm B. 准备开始 一台兼容的 Linux 主机。Kubernetes 项目为基于 Debian 和 Red Hat 的 Linux 发行版以及一些不提供包管理器的发行版提供通用的指令每…...

国有行面试:掌握这11个测评要素
银行笔试期一结束,面试也接连不断。大家做好拿下offer的准备了吗?回顾过往银行面试,半结构化和无领导题型备受考官喜爱,“有备无患,方能走向远方”,银行面试备考,了解掌握面试本质测评要素&…...

云视如何实现流量转化
云视如何实现流量转化 大家好我是小鱼 小伙伴很好奇 云视除了直播带货 打赏,广告 还有哪些方式 可以实现流量转化 今天我和大家分享一下这个话题 接下来我们要讲讲 我们要用的工具 优惠券 适用于刺激消费回流,构建闭环消费圈。 课程赠送 趣味推广营销&am…...

Metersphere+jar+beanshell+连接linux
Meterspherejarbeanshell连接linux java编写连接linux代码 使用jsch连接linux,下载jsch包或者使用maven <dependencies><dependency><groupId>com.jcraft</groupId><artifactId>jsch</artifactId><version>0.1.55<…...

前端开发工程师如何提升个人审美
✨求关注~ 😀博客:www.protaos.com 作为前端开发工程师,提升个人审美能力对于设计和开发出高质量的用户界面至关重要。个人审美是指对于颜色、布局、字体、图形等视觉元素的理解和判断能力。通过提升个人审美,前端开发工程师能够设…...

【软件测试】Python自动化软件测试算是程序员吗?
今天早上一觉醒来,突然萌生一个念头,【软件测试】软件测试算是程序员吗?左思右想,总感觉哪里不对。做了这么久的软件测试,还真没深究过这个问题。 基于,内事问百度的准则: 结果…… 我刚发出软…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
