离散数学 | 图论 | 欧拉图 | 哈密顿图 | 割点 | 桥(欧拉图和哈密顿图有没有割点和桥?)
本文主要解决以下几个问题:
1.欧拉图能不能有割点,能不能有桥?
2.哈密顿图能不能有割点,能不能有桥?
首先我们要明白几个定义
割点的定义就是在一个图G中,它本来是连通的,去掉一个点v以后这个图G就不连通了,那么点v就被叫做割点。
桥的定义就是在一个图G中,它本来也是连通的,去掉一条边x以后这个图就不连通了,那么边x就被称为桥。
欧拉图是拥有欧拉闭迹的图。
所谓欧拉闭迹,包含两层概念:“闭”和“迹”。
我们先来说什么是迹,所谓“迹”,就是用一笔可以从一个顶点出发,一直沿着边走,走到另一个顶点停止。在走的过程中,可以有重复的点,但是不能有重复的边。也就是说一个点可以经过两次以上,但是一个边只能走一次。
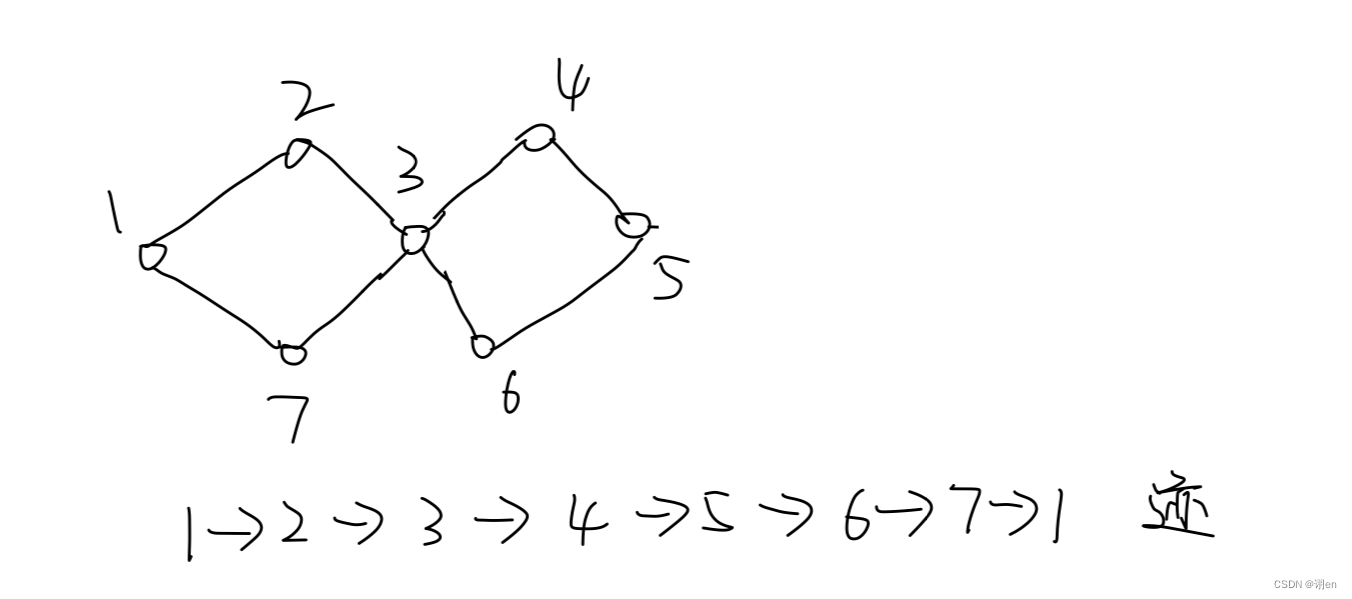
如图:从1走到5,最后再回到1,这就是一条迹。
我们再来说什么是“闭”,所谓闭,就是闭合的意思,也就是说这条迹最后要回到起点,形成一条闭合回路。上图所示的迹也是一条闭迹。
我们可以看到上面画的这个图拥有一套欧拉闭迹,那么他就是一个欧拉图。
如果这个图去掉点3,他就变成不连通的了,那么点3就是一个割点,显然欧拉图是可以有割点的,有割点的图也可以是欧拉图。
那么欧拉图能不能有桥呢?
我们先来试着想一想,欧拉图必须要从一个点出发走回去,边不能重复。那么如果有桥的话,对于两个划分以后的子图,我们为了从一个顶点出发,最后再回到这个顶点,不得不从这个桥走两遍,这显然违背了欧拉图的定义。
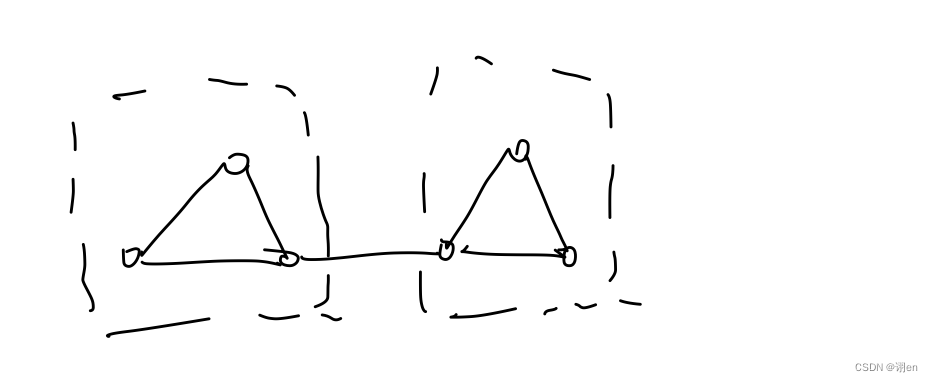
如果需要严谨证明的话,我们可以先由欧拉图得到,在图上任意去掉一条边x,图依然是连通的。如果去掉桥的话,恰恰与欧拉图的定义相违背,自然就证明了欧拉图中不能有桥了。
说完了欧拉图,我们来看哈密顿图。
哈密顿图是具有哈密顿圈的图,哈密顿圈是对于图G而言,它有一个圈,这个圈包含了图G的所有顶点。
换言之,如果一个图G,它具有一个能包含所有顶点的圈,那么它具有哈密顿圈,图G也就是哈密顿图了。
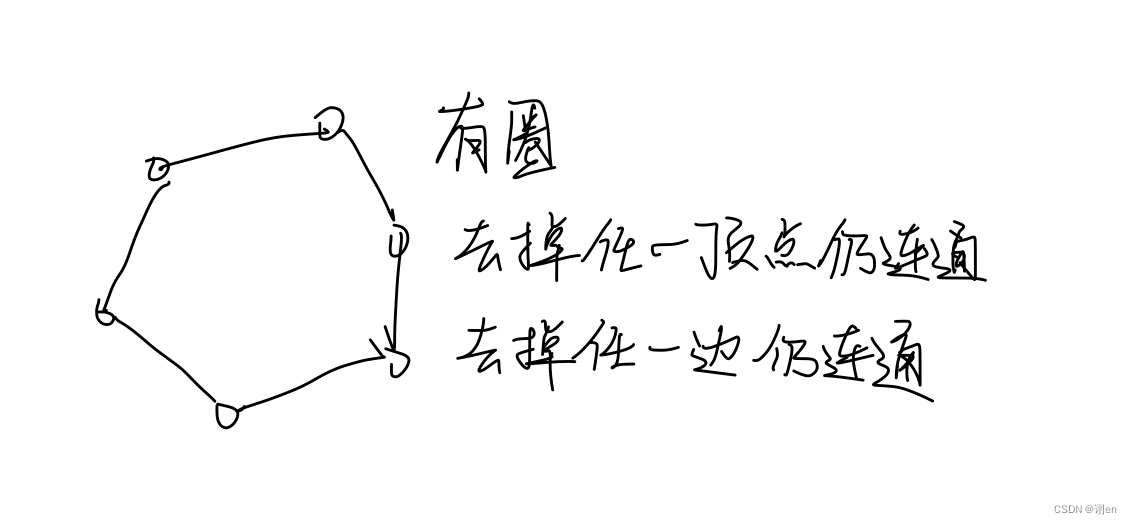
显然哈密顿图是有圈的图,有圈的图不论去掉哪个顶点依然是连通的,所以哈密顿图没有割点。有圈的图不论去掉哪条边也依然是连通的,所以哈密顿图也没有桥
换言之,有割点的图一定不是哈密顿图,有桥的图一定不是哈密顿图。
完毕!
相关文章:

离散数学 | 图论 | 欧拉图 | 哈密顿图 | 割点 | 桥(欧拉图和哈密顿图有没有割点和桥?)
本文主要解决以下几个问题: 1.欧拉图能不能有割点,能不能有桥? 2.哈密顿图能不能有割点,能不能有桥? 首先我们要明白几个定义 割点的定义就是在一个图G中,它本来是连通的,去掉一个点v以后这个…...

Android生命周期:理解与应用
摘要:Android生命周期是开发Android应用程序时至关重要的概念。本文将介绍Android生命周期的概念、生命周期方法的执行顺序以及如何在应用程序中正确地管理生命周期。我们还将讨论生命周期对于应用程序的重要性,并提供一些实际应用中的最佳实践和注意事项…...

00后真的是内卷王中王,真的想离职了....
都说00后躺平了,但是有一说一,该卷的还是卷。这不,前段时间我们公司来了个00年的,工作没两年,跳槽到我们公司起薪18K,都快接近我了。后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了。…...

linux Fd以及重定向讲解
感谢你的阅读,是对我最大的鼓励!!!! 目录 fd理解 文件操作重定向 让我们回顾C语言文件操作 首选我们要知道2个知识点: 额外知识点 如何理解一切皆文件呢? 当父进程fork创建子进程是否创建…...

Moonbeam近日提案公投一览
正在跟进Moonbeam治理的小伙伴,一起来快速浏览一下近期生态中正在发生的事情吧!其中包含多个去中心化应用的Grant加速计划提案、HRMP开拓提案以及优化质押相关平台的内容。许多提案都与网络的运作息息相关,一起了解和参与Moonbeam的发展吧&am…...

凝聚青年力量,打造数字化人才队伍
当代青年人勇于探索、敢于创新、勤于变革,积极承担社会责任。这与ABeam倡导的「Build Beyond As One.™」的品牌理念不谋而合。ABeam的青年员工是未来社会的中坚力量,也正用他们的青春能量助力ABeam在中国的发展。 01 新兴青年力量 对ABeam而言&#…...

蓝牙资讯|智能家居标准Matter 1.1 发布,智能家居产品兼容更丰富
据“CSA 连接标准联盟”官方微信号,Matter 1.1 版本已发布,“1.1 版本带来的更新使设备制造商和开发者上手更容易、产品获取认证更方便,也让产品能更快地交付给用户。该版本还为电池供电设备提供了更大支持,而这类设备涉及多种类型…...

Cube Map 系列之:手把手教你 实现天空盒(Sky Box)
什么是天空盒 An skybox is a box with textures on it to look like the sky in all directions or rather to look like what is very far away including the horizon.天空盒是一个使用纹理贴图构建的盒子,人在其中朝任何一个方向看去,其纹理彷佛天空…...

腾讯VS百度:在AI上下大赌注
来源:猛兽财经 作者:猛兽财经 腾讯控股(00700)最近已经把基础模型和生成式人工智能应用方面的行业突破视为其业务的新增长机会了,并且正在大力投资人工智能,从而增强其现有产品的竞争力和拓展新的机会,比如腾讯已经把…...
字节原来这么容易进,是面试官放水,还是公司实在是太缺人?
本人211非科班,之前在字节和腾讯实习过,这次其实没抱着什么特别大的希望投递,没想到字节可以再给我一次机会,还是挺开心的。 本来以为有个机会就不错啦!没想到能成功上岸,在这里要特别感谢帮我内推的同学&…...

生死疲劳|因为此书莫言获得诺贝尔奖
📚书名:《生死疲劳》 ✏️作者:莫言 历经六世的生死轮回, 三代人无尽的生死疲劳; 触碰极致的痛苦与快乐, 感受不灭的热情与希望。 🔥虽然本书长达39万字,但阅读过程却是无比的酣畅…...

Linux系统编程总结
day2 vim的三种工作模式 命令模式 vi hello.c zz 保存退出 2.编辑模式 i a o s (有大写)可以写东西 3.末行模式: 文本和末行模式不能直接切换 要切换回命令模式 再到末行模式,w:保存 q:退出 按两次esc回到命令模式 vim的基本…...
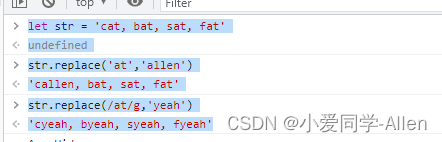
javascript基础二:Javscript字符串的常用方法有哪些?
在日常开发中,我们对字符串也是操作蛮多,这里我们来整理下字符串的一下最常用的方法 一、操作方法 字符串常用的操作方法归纳为增、删、改、查 增 这里增的意思并不是说直接增添内容,而是创建字符串的一个副本,再进行操作 除了…...
面了个 Java 实习生,小伙很优秀!
大家好,我是鱼皮,前几天给自己的公司面试了一位 Java 暑期实习生,候选人目前是大三。 整个过程我都录屏了,并且在征得候选人的同意后,把面试过程分享出来。一方面是希望对其他在学编程找工作的小伙伴有一些启发和参考…...
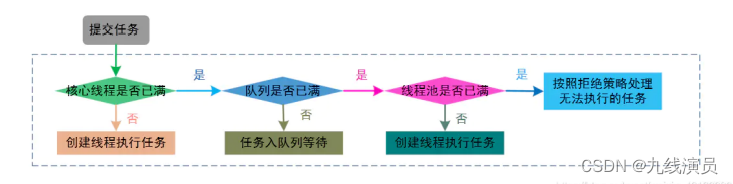
Java -并发(多线程)-Interview面试题收集
1、多线程并发 1)多线程中 synchronized 锁升级的原理是什么? synchronized 锁升级原理:在锁对象的对象头里面有一个 threadid 字段,在第一次访问的时候 threadid 为空,jvm 让其持有偏向锁,并将 threadid…...
方法)
HashMap的merge()方法
最近遇到一个需求,需要统计各个会员的正在履行合同的合同租金总计,以此作为制定会员等级的标准。但是之前这个方法其实是有的,只是写的乱七八糟,具体的代码就不太方便放上来,就说说大致的代码思路吧。 原代码思路是先查…...
)
用 mysql_secure_installation 工具来进行密码重置操作(有效)
mysql_secure_installation 工具用于在 MariaDB 中进行一些安全设置,包括重置 root 用户的密码。您可以按照以下步骤使用该工具来重置 root 用户的密码: 1. 以管理员身份登录到您的系统。 2. 执行以下命令以运行 mysql_secure_installation 工具&#…...
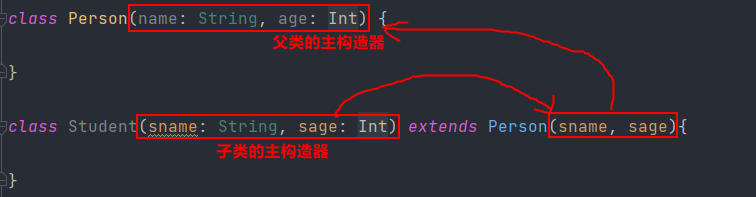
【Scala---02】Scala 类与对象 『 类 | 属性 | 访问权限 | 方法 | 继承 | 伴生对象伴生类』
文章目录 1. 定义类2. 属性3. 访问权限4. 方法4.1 方法 vs 函数4.2 方法重写4.3 方法重载4.4 构造方法(1) 构造器定义(2) 构造器的参数列表(3) 构造器私有化 5. 继承6. 伴生对象 & 伴生类6.1 伴生对象的由来6.2 伴生对象 & 伴生类 7. 后续 1. 定义类 Java文件…...
))
一文掌握python列表的所有使用方法(零基础学python(一))
列表 Python 中的列表是一种可变的数据类型,它可以存储多个值,并且可以随时添加、删除或修改其中的元素。以下是 Python 列表的基本操作和示例代码: 创建列表 可以使用方括号 [] 来创建一个空列表,也可以在方括号中添加元素来创建一个非空列表。例如: empty_list = [] …...

头歌计算机组成原理实验—运算器设计(6)第6关:5位无符号阵列乘法器设计
第6关:5位无符号阵列乘法器设计 实验目的 帮助学生掌握阵列乘法器的实现原理,能够分析阵列乘法器的性能,能在 Logisim 中绘制阵列乘法器电路。 视频讲解 实验内容 在 Logisim 中打开 alu.circ 文件,在5位阵列乘法器中实现斜向…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
