当前位置： 首页 > news >正文

使用AES算法加密技术集成Java和Vue保护您的数据，代码示例和算法原理

news 2026/2/8 18:42:56

1 算法的原理：

AES是一种对称加密算法，也就是说加密和解密使用的是同一个密钥。其基本原理是将明文分成固定大小的块（128位），然后使用密钥对每个块进行加密操作，最后生成密文。在加密过程中，还需要使用一个向量（IV）来增加安全性，避免相同的明文块生成相同的密文块。解密过程则是将密文块解密成明文块，再将明文块拼接起来，最终还原原始的明文。

2 需要引入的依赖和安装的包

以下是使用Maven进行构建时需要添加的依赖项：
xml

<dependencies><dependency><groupId>javax.crypto</groupId>

相关文章：

使用AES算法加密技术集成Java和Vue保护您的数据，代码示例和算法原理

1 算法的原理： AES是一种对称加密算法，也就是说加密和解密使用的是同一个密钥。其基本原理是将明文分成固定大小的块（128位），然后使用密钥对每个块进行加密操作，最后生成密文。在加密过程中，还需要使用一个向量（IV）来增加安全性，避免相同的明文块生成相同的密文块。…...

编程日记 2023/5/25 0:48:16

vcruntime140_1.dll丢失怎样修复，推荐4个vcruntime140_1.dll丢失的修复方法

vcruntime140_1.dll文件是Microsoft Visual C Redistributable for Visual Studio 2015运行库的一部分&#xff0c;它是一个用于支持Visual C构建的应用程序的系统文件。这个文件包含了在运行C程序时所需要的函数和类库&#xff0c;主要负责向应用程序提供运行时环境。如果电脑…...

编程日记 2023/5/25 0:43:15

快来试试这几个简单好用的手机技巧吧

技巧一&#xff1a;相机功能 苹果手机的相机功能确实非常出色&#xff0c;除了出色的像素之外&#xff0c;还有许多其他实用功能可以提升拍摄体验。 这些相机功能提供了更多的选择和便利性&#xff0c;使用户能够更好地适应不同的拍摄需求。 自拍功能&#xff1a;通过选择自…...

编程日记 2023/6/1 7:57:03

OneDrive同步角标消失 - 解决方案

问题 在电脑端使用OneDrive时&#xff0c;文件管理器OneDrive文件夹内的文件会在左下角显示同步状态&#xff0c;如下图。若没有显示同步角标&#xff0c;则此功能出现异常&#xff0c;下文介绍如何显示同步角标。 值得一提的是&#xff0c;同步角标只起到显示作用&#xff0…...

编程日记 2023/5/25 0:33:12

自学网络安全【黑客】，一般人我劝你还是算了吧

前言&#xff1a;我是劝一般人算了&#xff0c;看你是一般人还是。。。 一、网络安全学习的误区 1.不要试图以编程为基础去学习网络安全2.不要刚开始就深度学习网络安全3.收集适当的学习资料4.适当的报班学习二、学习网络安全的些许准备 1.硬件选择2.软件选择3.外语能力三、网…...

编程日记 2023/5/31 13:57:00

Java集合工具：first和last

在平常开发过程中&#xff0c;我们经常会遇到截取列表片段的需求&#xff0c;比如取列表中前4个元素、取后四个元素。Java的List提供了subList方法&#xff0c;可以用来完成这些工作&#xff0c;但是使用起来并没有那么便利&#xff0c;比如取前四个元素&#xff1a; list.sub…...

编程日记 2023/5/31 14:20:43

leetcode 905. 按奇偶排序数组

题目描述解题思路执行结果 leetcode 905. 按奇偶排序数组 题目描述 按奇偶排序数组 给你一个整数数组 nums&#xff0c;将 nums 中的的所有偶数元素移动到数组的前面&#xff0c;后跟所有奇数元素。 返回满足此条件的 任一数组 作为答案。 示例 1&#xff1a; 输入&#xff1a;…...

编程日记 2023/5/25 0:18:00

密码学安全性证明（一）Cramer-Shoup密码系统

Cramer-Shoup密码系统来自于A Practical Public Key CryptosystemProvably Secure against Adaptive ChosenCiphertext Attack这篇论文 CDH问题回顾&#xff1a; 已知(g,g^x, gk)能否计算gxk DDH问题回顾&#xff1a; 已知(g,g^x, g^k &#xff0c;D)能否判断D是否等于g^xk 注意…...

编程日记 2023/5/25 0:12:59

Asp.net Core系列学习（1）

Asp.net Core 6系列学习 文章目录 Asp.net Core 6系列学习Asp.net Core 概述一、在 ASP.NET 4.x 和 ASP.NET Core 之间进行选择二、适用于服务器应用的 .NET 与 .NET Framework三、ASP.NET Core Web UI1.服务器和客户端呈现 UI 的优势和成本2.服务器呈现的 UI 四、可用的 ASP.N…...

编程日记 2023/5/25 0:07:58

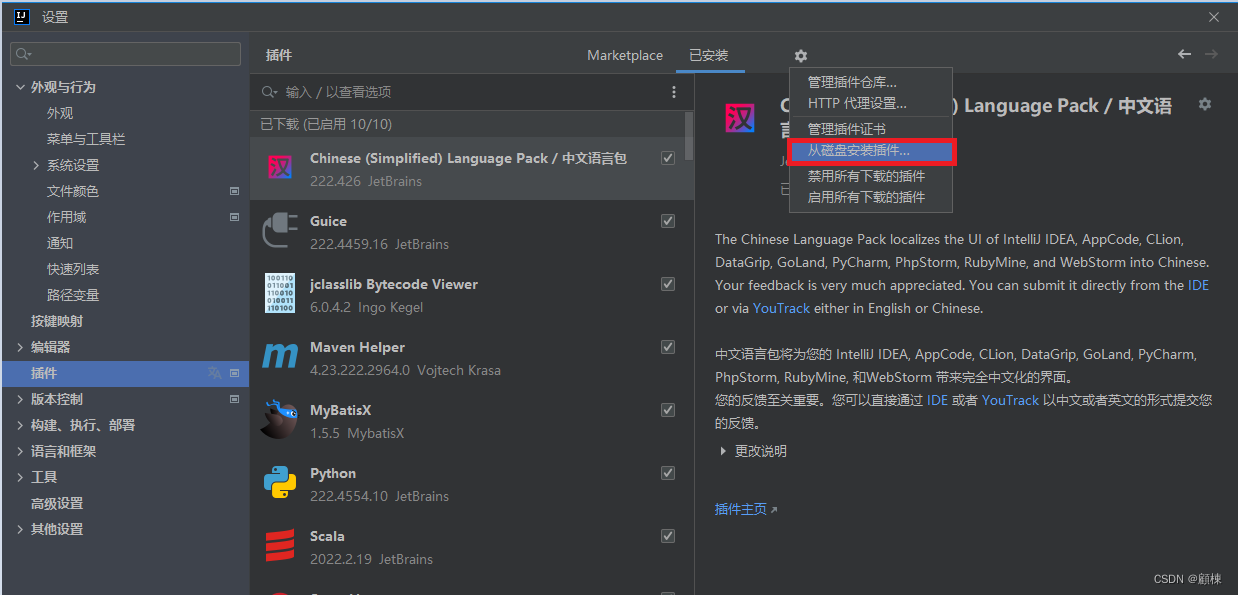
IDEA 2022.2 安装以及自定义优化

IDEA2022.2 安装以及自定义优化 文章目录 IDEA2022.2 安装以及自定义优化安装图解获取激活码自定义优化文件编码设置设置类文档注释和方式注释模板方法分割线 常用插件离线安装 安装图解 静默卸载&#xff08;旧版本的设置和配置将不会被删除&#xff09; 获取激活码 略…...

编程日记 2023/5/25 0:02:57

【华为OD机试真题2023B卷 JAVA】阿里巴巴找黄金宝箱(II)

华为OD2023（B卷）机试题库全覆盖，刷题指南点这里 阿里巴巴找黄金宝箱(II) 知识点数组哈希表优先级队列 时间限制：1s 空间限制：256MB 限定语言：不限 题目描述： 一贫如洗的樵夫阿里巴巴在去砍柴的路上，无意中发现了强盗集团的藏宝地，藏宝地有编号从0~N的箱子，每个箱子上…...

编程日记 2023/5/24 23:57:56

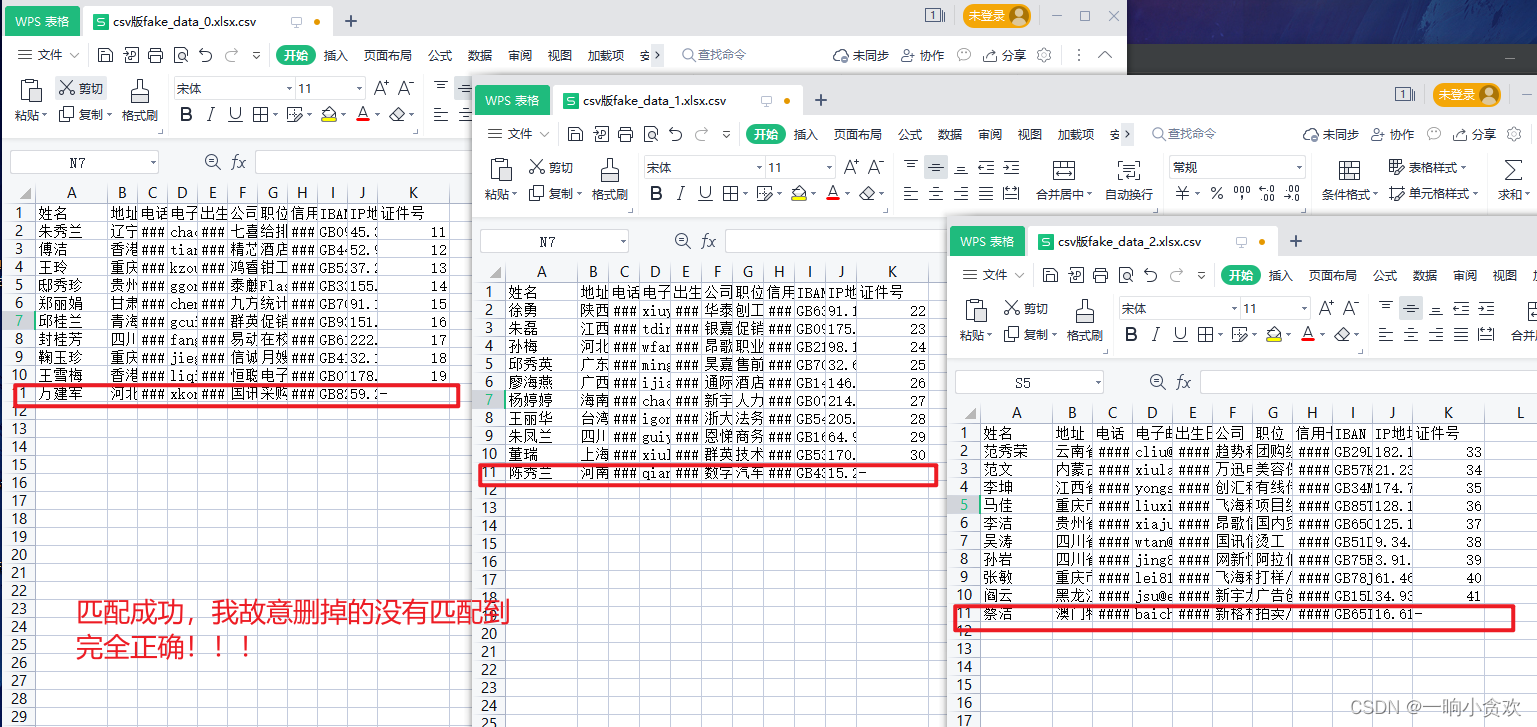
Python对Excel文件多表对多表之间的匹配(两种不同表头)——之json版

首先Excel文件多表对多表之间的匹配(VLOOKUP),有多种办法&#xff0c; 1&#xff1a;将Excel文件导入Mysql或其他数据库,然后将两种表合并成一张表&#xff0c;接着用数据库匹配 2&#xff1a;将两种表内容&#xff0c;复制粘贴到一起&#xff0c;各自分别保存成一张表&#xf…...

编程日记 2023/5/24 23:52:55

shiro环境搭建

源码部署 这种方法相对复杂&#xff0c;如果不需要分析源码直接用docker就行 前置条件&#xff1a;Maven Ideal Tomcat 下载方式1&#xff1a;https://codeload.github.com/apache/shiro/zip/shiro-root-1.2.4&#xff0c;然后将文件夹导入ideal下载方式2&#xff1a;将shiro…...

编程日记 2023/5/24 23:47:54

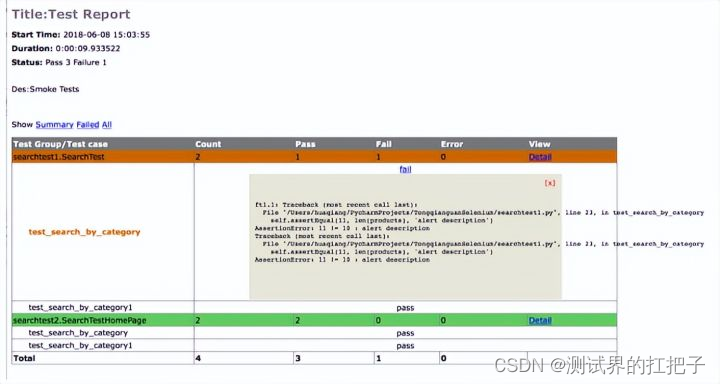
一文读懂selenium自动化测试（基于Python）

前言 我们今天来聊聊selenium自动化测试&#xff0c;我们都知道selenium是一款web自动化测试的工具&#xff0c;它应该如何去运用呢?我们接着看下去。 ​1、Selenium简介&#xff1a; 1.1 Selenium&#xff1a; Selenium是一款主要用于Web应用程序自动化测试的工具集合。Sele…...

编程日记 2023/5/24 23:42:53

如何高效地在网上找开源项目

开源项目是发展技能、分享想法和成为开发社区一员的好方法。开源意味着软件功能背后的源代码与所有想要阅读它的人公开共享。这意味着你可以准确地看到一个系统是如何工作的——一旦你愿意冒险&#xff0c;就为它做出贡献。除了向所有人开放贡献外&#xff0c;这种开放代码库通…...

编程日记 2023/5/24 23:37:52

2023系统分析师---冲刺资料必备知识点三

视图的优点&#xff1a; 视图能简化用户的操作&#xff1b;视图机制可以使用户以不同的方式查询同一数据&#xff1b;视图对数据库重构提供了一定程度的逻辑独立性&#xff1b;视图可以对机密的数据提供安全保护&#xff1b; ER图、实体、联系、联系的类型&#xff1a; 分布…...

编程日记 2023/5/24 23:32:51

集成Bean Validation 1.1(JSR-349)到 SpringMVC

Spring4新特性——集成Bean Validation 1.1(JSR-349)到 SpringMVC Bean Validation 1.1当前实现是Hibernate validator 5&#xff0c;且spring4才支持。接下来我们从以下几个方法 讲解Bean Validation 1.1&#xff0c;当然不一定是新特性&#xff1a; 1. 集成Bean Valida…...

编程日记 2023/5/29 15:10:32

【软考中级】软件设计师选择题题集（一）

海明校验码是在n个数据位之外增设k个校验位，从而形成一个k+n位的新的码字， 使新的码字的码距比较均匀地拉大。n与k的关系是（1)。 (1)A.2k - 1≥n + k  B.2n - 1≤ n + k   C.n = k  D.n-1≤k 【答案】A 【解析】 【答案】B A 【解析】 在采用结构化方法进行系统分析时，…...

编程日记 2023/5/24 23:22:49

10个炫酷特效的网页写法（附源码），拿去就能用，奈斯奈斯

这是我借鉴其他博主的&#xff0c;给网页加个背景&#xff0c;给鼠标加个特效&#xff0c;“使用简单”&#xff0c;“效果爆炸”的页面&#xff0c;分享给大家&#xff0c;如果觉得有帮助可以点赞收藏支持一下&#xff0c;如果能关注一下就再好不过了。 内容转载于https://bl…...

编程日记 2023/5/24 23:17:48

vscode开发stm32的编译环境配置教程

文章目录 1. 背景2. 配置步骤2.1. vscode插件安装2.2. 新建工程2.3. 配置编译环境2.3.1. 芯片支持2.3.2. 编译器选择2.3.3. CPU类型2.3.4. 硬件浮点选项2.3.5. 使用自定义的链接脚本2.3.6. RAM/FLASH布局2.3.7. 构建器选项2.4. 编译3. 问题汇总3.1. 浮点编译开关3.2. MicroLIB编…...

编程日记 2023/5/24 23:12:46

Chapter03-Authentication vulnerabilities

文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

编程新知 2026/2/7 4:57:53

python打卡day49

知识点回顾&#xff1a; 通道注意力模块复习空间注意力模块CBAM的定义 作业&#xff1a;尝试对今天的模型检查参数数目&#xff0c;并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

编程新知 2026/2/7 5:37:17

基于服务器使用 apt 安装、配置 Nginx

&#x1f9fe; 一、查看可安装的 Nginx 版本 首先&#xff0c;你可以运行以下命令查看可用版本&#xff1a; apt-cache madison nginx-core输出示例&#xff1a; nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

编程新知 2026/1/9 12:53:59

基础测试工具使用经验

背景 vtune&#xff0c;perf, nsight system等基础测试工具&#xff0c;都是用过的&#xff0c;但是没有记录&#xff0c;都逐渐忘了。所以写这篇博客总结记录一下&#xff0c;只要以后发现新的用法&#xff0c;就记得来编辑补充一下 perf 比较基础的用法&#xff1a; 先改这…...

编程新知 2025/11/22 7:38:58

【Zephyr 系列 10】实战项目：打造一个蓝牙传感器终端 + 网关系统（完整架构与全栈实现）

🧠关键词：Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者：希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数：约 5200 字 ✨ 项目总览 在物联网实际项目中，**“终端 + 网关”**是…...

编程新知 2026/1/31 6:12:22

Android Bitmap治理全解析：从加载优化到泄漏防控的全生命周期管理

引言 Bitmap&#xff08;位图&#xff09;是Android应用内存占用的“头号杀手”。一张1080P&#xff08;1920x1080&#xff09;的图片以ARGB_8888格式加载时&#xff0c;内存占用高达8MB&#xff08;192010804字节&#xff09;。据统计&#xff0c;超过60%的应用OOM崩溃与Bitm…...

编程新知 2026/1/8 22:17:14

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统

目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索&#xff08;基于物理空间 广播范围&#xff09;2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

编程新知 2025/12/12 6:01:17

rnn判断string中第一次出现a的下标

# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

编程新知 2025/9/24 16:25:00

如何更改默认 Crontab 编辑器 ？

在 Linux 领域中&#xff0c;crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用&#xff0c;用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益&#xff0c;允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

编程新知 2026/1/30 3:27:35

关于uniapp展示PDF的解决方案

在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项&#xff1a; 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库&#xff1a; npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

编程新知 2025/9/18 20:16:52