14- 决策树算法 (有监督学习) (算法)
- 决策树是属于有监督机器学习的一种
- 决策树算法实操:
from sklearn.tree import DecisionTreeClassifier
# 决策树算法
model = DecisionTreeClassifier(criterion='entropy',max_depth=d)
model.fit(X_train,y_train)
1、决策树概述
决策树是属于有监督机器学习的一种,起源非常早,符合直觉并且非常直观,模仿人类做决策的过程,早期人工智能模型中有很多应用,现在更多的是使用基于决策树的一些集成学习的算法。这一章我们把决策树算法理解透彻了,非常有利于后面去学习集成学习。
1.1、示例一
上表根据历史数据,记录已有的用户是否可以偿还债务,以及相关的信息。通过该数据,构建的决策树如下:
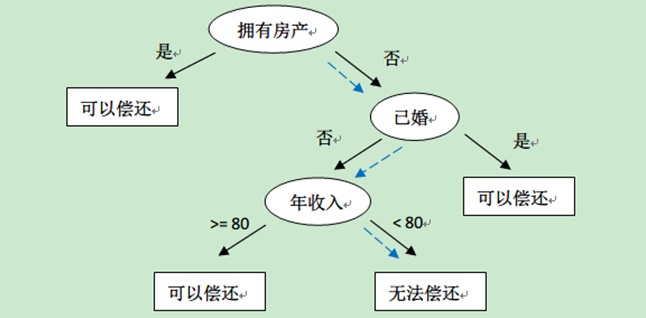
1.2、决策树算法特点
-
可以处理 非线性的问题
-
可解释性强,没有方程系数
-
模型简单,模型预测效率高 if else
2、DecisionTreeClassifier使用
2.1、算例介绍
账号是否真实跟属性:日志密度、好友密度、是否使用真实头像有关系~
2.2、构建决策树并可视化
数据创建
import numpy as np
import pandas as pd
y = np.array(list('NYYYYYNYYN'))
print(y)
X = pd.DataFrame({'日志密度':list('sslmlmmlms'),'好友密度':list('slmmmlsmss'),'真实头像':list('NYYYYNYYYY'),'真实用户':y})
数据调整
X['日志密度'] = X['日志密度'].map({'s':0,'m':1,'l':2})
X['好友密度'] = X['好友密度'].map({'s':0,'m':1,'l':2})
X['真实头像'] = X['真实头像'].map({'N':0,'Y':1})
X['真实用户'] = X['真实用户'].map({'N':0,'Y':1})模型训练可视化
import matplotlib.pyplot as plt
from sklearn import tree
# 使用信息熵,作为分裂标准
model = DecisionTreeClassifier(criterion='entropy')
model.fit(X,y)
plt.rcParams['font.family'] = 'STKaiti'
plt.figure(figsize=(12,16))
fn = X.columns
_ = tree.plot_tree(model,filled = True,feature_names=fn)
plt.savefig('./iris.jpg')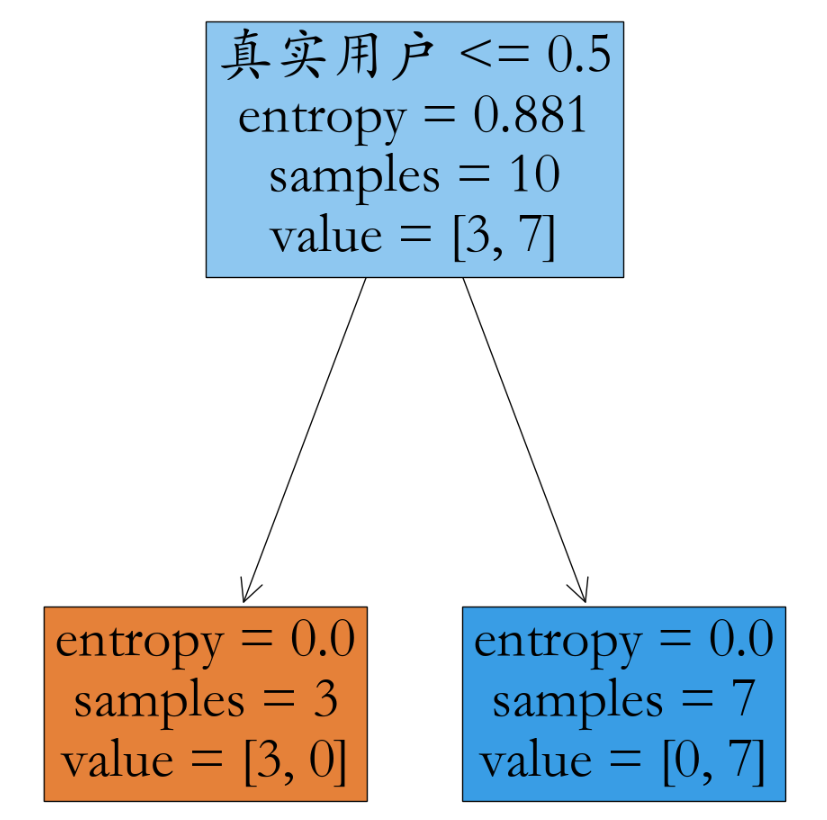
2.3、信息熵
-
构建好一颗树,数据变的有顺序了(构建前,一堆数据,杂乱无章;构建一颗,整整齐齐,顺序),用什么度量衡表示,数据是否有顺序:信息熵 。
-
物理学,热力学第二定律(熵),描述的是封闭系统的混乱程度 。
2.4、信息增益
信息增益是知道了某个条件后,事件的不确定性下降的程度。写作 g(X,Y)。它的计算方式为熵减去条件熵,如下:
表示的是,知道了某个条件后,原来事件不确定性降低的幅度。
2.5、手动计算实现决策树分类
s = X['真实用户']
p = s.value_counts()/s.size
(p * np.log2(1/p)).sum() # 0.8812908992306926x = X['日志密度'].unique()
x.sort()
# 如何划分呢,分成两部分
for i in range(len(x) - 1):split = x[i:i+2].mean()cond = X['日志密度'] <= split# 概率分布p = cond.value_counts()/cond.size# 按照条件划分,两边的概率分布情况indexs =p.indexentropy = 0for index in indexs:user = X[cond == index]['真实用户']p_user = user.value_counts()/user.sizeentropy += (p_user * np.log2(1/p_user)).sum() * p[index]print(split,entropy)columns = ['日志密度','好友密度','真实头像']
lower_entropy = 1
condition = {}
for col in columns:x = X[col].unique()x.sort()print(x)# 如何划分呢,分成两部分for i in range(len(x) - 1):split = x[i:i+2].mean()cond = X[col] <= split# 概率分布p = cond.value_counts()/cond.size# 按照条件划分,两边的概率分布情况indexs =p.indexentropy = 0for index in indexs:user = X[cond == index]['真实用户']p_user = user.value_counts()/user.sizeentropy += (p_user * np.log2(1/p_user)).sum() * p[index]print(col,split,entropy)if entropy < lower_entropy:condition.clear()lower_entropy = entropycondition[col] = split
print('最佳列分条件是:',condition)
3、决策树分裂指标
常用的分裂条件时:
-
信息增益
-
Gini系数
-
信息增益率
-
MSE(回归问题)
3.1、信息熵(ID3)
在信息论里熵叫作信息量,即熵是对不确定性的度量。从控制论的角度来看,应叫不确定性。信息论的创始人香农在其著作《通信的数学理论》中提出了建立在概率统计模型上的信息度量。
对应公式:
3.2、Gini系数(CART)
基尼系数是指国际上通用的、用以衡量一个国家或地区居民收入差距的常用指标。
基尼系数最大为“1”,最小等于“0”。基尼系数越接近 0 表明收入分配越是趋向平等。国际惯例把 0.2 以下视为收入绝对平均,0.2-0.3 视为收入比较平均;0.3-0.4 视为收入相对合理;0.4-0.5 视为收入差距较大,当基尼系数达到 0.5 以上时,则表示收入悬殊。
3.3、MSE
用于回归树,后面章节具体介绍
4、鸢尾花分类代码实战
4.1、决策树分类鸢尾花数据集
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import tree
import matplotlib.pyplot as pltX,y = datasets.load_iris(return_X_y=True)# 随机拆分
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 256)# max_depth调整树深度:剪枝操作
# max_depth默认,深度最大,延伸到将数据完全划分开为止。
model = DecisionTreeClassifier(max_depth=None,criterion='entropy')
model.fit(X_train,y_train)
y_ = model.predict(X_test)
print('真实类别是:',y_test)
print('算法预测是:',y_)
print('准确率是:',model.score(X_test,y_test))
# 决策树提供了predict_proba这个方法,发现这个方法,返回值要么是0,要么是1
model.predict_proba(X_test)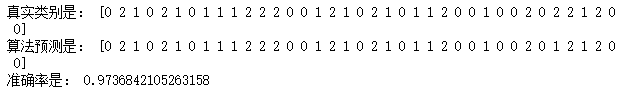
4.2、决策树可视化
import graphviz
from sklearn import tree
from sklearn import datasets
# 导出数据
iris = datasets.load_iris(return_X_y=False)
dot_data = tree.export_graphviz(model,feature_names=fn,class_names=iris['target_names'],# 类别名filled=True, # 填充颜色rounded=True,)
graph = graphviz.Source(dot_data)
graph.render('iris')4.3、选择合适的超参数并可视化
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import tree
import matplotlib.pyplot as pltX,y = datasets.load_iris(return_X_y=True)# 随机拆分
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 256)
depth = np.arange(1,16)
err = []
for d in depth:model = DecisionTreeClassifier(criterion='entropy',max_depth=d)model.fit(X_train,y_train)score = model.score(X_test,y_test)err.append(1 - score)print('错误率为%0.3f%%' % (100 * (1 - score)))
plt.rcParams['font.family'] = 'STKaiti'
plt.plot(depth,err,'ro-')
plt.xlabel('决策树深度',fontsize = 18)
plt.ylabel('错误率',fontsize = 18)
plt.title('筛选合适决策树深度')
plt.grid()
plt.savefig('./14-筛选超参数.png',dpi = 200)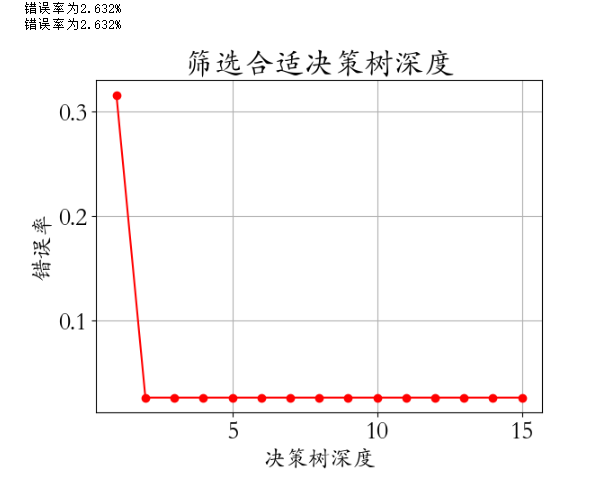
相关文章:

14- 决策树算法 (有监督学习) (算法)
决策树是属于有监督机器学习的一种决策树算法实操: from sklearn.tree import DecisionTreeClassifier # 决策树算法 model DecisionTreeClassifier(criterionentropy,max_depthd) model.fit(X_train,y_train)1、决策树概述 决策树是属于有监督机器学习的一种,起源…...

如何编译和运行C++程序?
C 和C语言类似,也要经过编译和链接后才能运行。在《C语言编译器》专题中我们讲到了 VS、Dev C、VC 6.0、Code::Blocks、C-Free、GCC、Xcode 等常见 IDE 或编译器,它们除了可以运行C语言程序,还可以运行 C 程序,步骤是一样的&#…...

Golang 给视频添加背景音乐 | Golang工具
目录 前言 环境依赖 代码 总结 前言 本文提供给视频添加背景音乐,一如既往的实用主义。 主要也是学习一下golang使用ffmpeg工具的方式。 环境依赖 ffmpeg环境安装,可以参考我的另一篇文章:windows ffmpeg安装部署_阿良的博客-CSDN博客 …...

让AI护理医疗:解决卫生系统的痛点
一、引言 1.对医疗领域中AI技术的介绍 随着人工智能的不断发展,它已经成为了各个领域中的重要组成部分。在医疗领域中,AI技术也逐渐发挥着越来越重要的作用。从诊断到治疗,从健康管理到研究,人工智能已经深刻地影响着医疗领域的…...
Windows 离线安装 MySQL 8
目录 1. 下载离线安装包 2. 上传解压 3 配置 my.ini 文件 4 设置系统环境变量 5 安装 MySQL 6 登录 MySQL 客户环境是内网环境,不能访问外网,只能离线安装 MySQL 了。 1. 下载离线安装包 MySQL 离线压缩包官网下载地址:MySQL :: Down…...

【前端攻城狮之vue基础】02路由+嵌套路由+路由query/params传参+路由props配置+replace属性+编程式路由导航+缓存路由组件
路由的基础知识1.路由简介2.路由基本使用3.嵌套路由4.传递路由的query传参# 5.传递路由的params参数6.路由的props传参配置7.路由router-link标签的replace属性8.编程式路由导航9.缓存路由组件1.路由简介 路由是一条条对应的key-value关系,key就是前端地址栏的路径…...
CHAPTER 1 Zabbix介绍及安装
Zabbix介绍及安装1.1 Zabbix监控1 为什么要监控1.1 网站可用性2 监控什么东西2.1 监控范畴3 怎么来监控3.1 远程管理服务器3.2 监控硬件3.3 查看cpu相关3.4 内存3.5 磁盘3.6 监控网络4 监控工具总览5 zabbix介绍5.1 zabbix的组成5.2 zabbix监控范畴1.2 安装zabbix1 环境检查2 安…...

认识V模型、W模型、H模型
软件测试与软件工程息息相关,软件测试是软件工程组成中不可或缺的一部分。 在软件工程、项目管理、质量管理得到规范化应用的企业,软件测试也会进行得比较顺利,软件测试发挥的价值也会更大。 要关注软件工程、质量管理以及配置管理与软件测试…...

excel ttest检测
1、excel函数含义 TTEST(array1,array2,tails,type) ▪ Array1: 第一组数据集 ▪ Array2: 第二组数据集 ▪ Tails: 用于定义所返回的分布的尾数: 1 代表单尾;2 代表双尾 ▪ Type: 用于定义 t-检验的类型: 1 代表成对检验;2 代表双样本等方差假设&am…...
PDFPrinting.Net操作进行细粒度控制
PDFPrinting.Net操作进行细粒度控制 PDFPrinting.Net能够容易且灵活地预测完美的打印结果以及用户文件的示例性显示。可以快速浏览.NET PDF打印中最关键的元素。如果用户需要获得更详细的概述,那么他可以查看快速入门手册,甚至是现有文档的详细概述参考。…...

SegPGD
在这项工作中,我们提出了一种有效和高效的分割攻击方法,称为SegPGD。此外,我们还提供了收敛性分析,表明在相同次数的攻击迭代下,所提出的SegPGD可以创建比PGD更有效的对抗示例。此外,我们建议应用我们的Seg…...
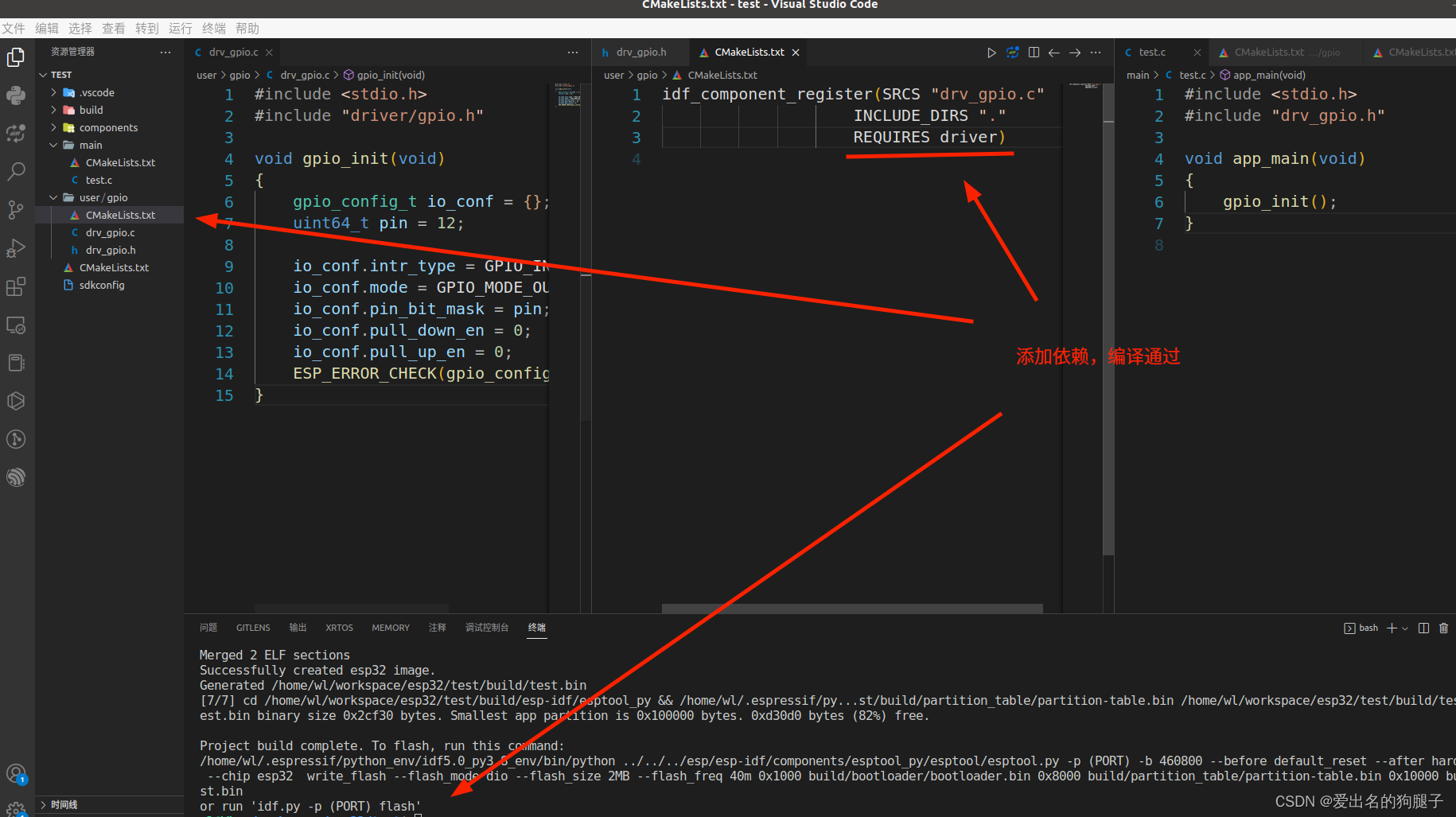
ESP-IDF + Vscode ESP32 开发环境搭建以及开发入门
ESP-IDF Vscode ESP32 开发环境搭建以及开发入门 文章目录ESP-IDF Vscode ESP32 开发环境搭建以及开发入门1. 前言2. 下载开发工具3. 配置工具4. 创建工程5. 解决vscode找不到头文件,波浪线警告6. 添加自己的组件6.1 组件说明6.2 添加项目组件6.3 添加扩展组件7. …...

SpringMvc的请求和响应
SpringMvc的数据响应 1.springmvc的数据相应方式 (1)页面跳转 直接返回字符串 通过ModelAndView对象返回 (2)回写数据 直接返回字符串 返回对象或集合 页面跳转 jsp页面 <% page contentType"text/html;charsetUTF-8&q…...

【Vue3】首页主体-面板组件封装
首页主体-面板组件封装 新鲜好物、人气推荐俩个模块的布局结构上非常类似,我们可以抽离出一个通用的面板组件来进行复用 目标:封装一个通用的面板组件 思路分析 图中标出的四个部分都是可能会发生变化的,需要我们定义为可配置主标题和副标题…...

部署 K8s 集群
1 .部署k8s的两种方式目前生产部署Kubernetes集群主要有两种方式:kubeadmKubeadm是一个K8s部署工具,提供kubeadm init和kubeadm join,用于快速部署Kubernetes集群。二进制包从github下载发行版的二进制包,手动部署每个组件&#x…...

关于北京君正:带ANC的2K网络摄像头用户案例
如果远程办公是您的未来,或者您经常通过视频通话与远方的朋友和亲戚交谈,那么您可以考虑购买网络摄像头以显著改善您的沟通。Anker PowerConf C200是个不错的选择。 Anker PowerConf C200专为个人工作空间而设计,能够以每秒30帧的速度拍摄2K…...
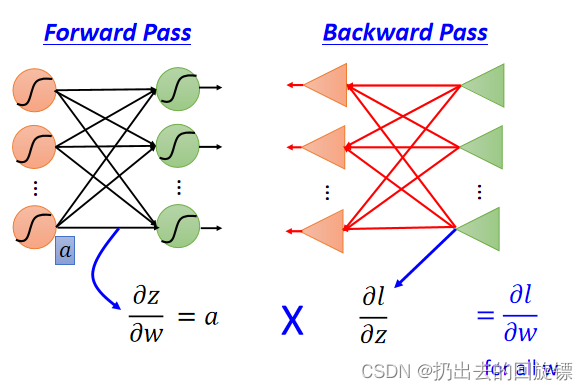
ccc-Backpropagation-李宏毅(7)
文章目录NotationBackpropagationForward passBackward passSummaryNotation 神经网络求解最优化Loss function时参数非常多,反向传播使用链式求导的方式提升计算梯度向量时的效率,链式法则如下: Backpropagation 损失函数计算为所有样本…...
找出字符串中第一个匹配项的下标-力扣28-java
一、题目描述给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。示例 1:输入:hayst…...

SpringBoot 监听Redis key过期回调
SpringBoot 监听Redis key过期回调 场景 Spring boot实现监听Redis key失效事件可应对某些场景例如:处理订单过期自动取消、用户会员到期… 开启Redis键过期回调通知 Redis默认是没有开启键过期监听功能的,需要手动在配置文件中修改。Linux操作系统 修…...

蓝桥杯C/C++VIP试题每日一练之回形取数
💛作者主页:静Yu 🧡简介:CSDN全栈优质创作者、华为云享专家、阿里云社区博客专家,前端知识交流社区创建者 💛社区地址:前端知识交流社区 🧡博主的个人博客:静Yu的个人博客 🧡博主的个人笔记本:前端面试题 个人笔记本只记录前端领域的面试题目,项目总结,面试技…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
qt+vs Generated File下的moc_和ui_文件丢失导致 error LNK2001
qt 5.9.7 vs2013 qt add-in 2.3.2 起因是添加一个新的控件类,直接把源文件拖进VS的项目里,然后VS卡住十秒,然后编译就报一堆 error LNK2001 一看项目的Generated Files下的moc_和ui_文件丢失了一部分,导致编译的时候找不到了。因…...
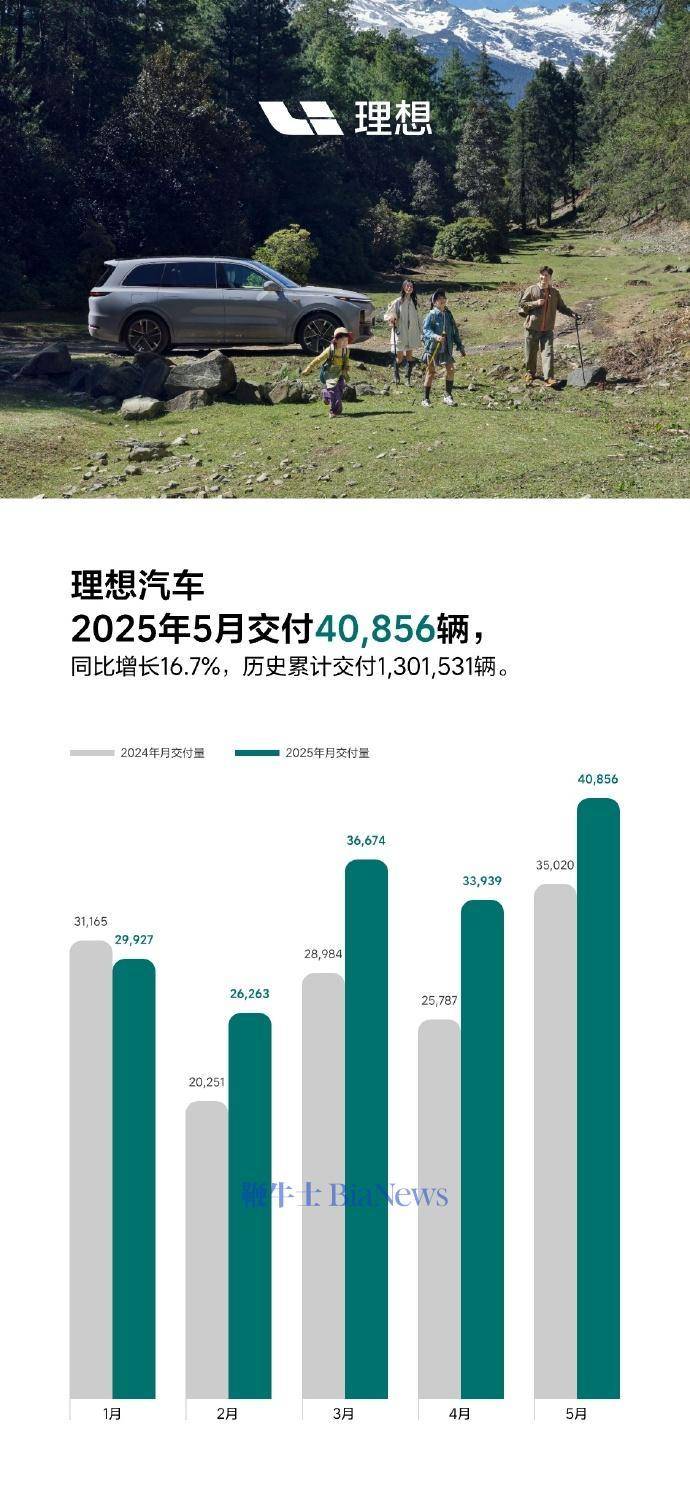
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...

STL 2迭代器
文章目录 1.迭代器2.输入迭代器3.输出迭代器1.插入迭代器 4.前向迭代器5.双向迭代器6.随机访问迭代器7.不同容器返回的迭代器类型1.输入 / 输出迭代器2.前向迭代器3.双向迭代器4.随机访问迭代器5.特殊迭代器适配器6.为什么 unordered_set 只提供前向迭代器? 1.迭代器…...
