2023.2.14每日一题——455. 分发饼干
每日一题
- 题目描述
- 解题核心
- 解法一:双指针
题目描述
题目链接:455. 分发饼干
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸s[j]。如果 s[j] >= g[i],我们可以将这个饼干j分配给孩子i,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值
示例 1
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。
示例 2
输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.
提示
- 1 <=
g.length<= 3 * 104 - 0 <=
s.length<= 3 * 104 - 1 <=
g[i], s[j]<= 231 - 1
解题核心
g和s的长度就是孩子和饼干的数量,尽可能多的分配给孩子就可以,一个饼干的最大价值就是分配给胃口刚好这么大的孩子
解法一:双指针
当前饼干尺寸符合孩子胃口就记录并且都移动到下一个位置,否则当前饼干就失去价值且移动到下一个
public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int gIndex = 0;int sIndex = 0;while (sIndex != s.length && gIndex != g.length) {if (g[gIndex] <= s[sIndex]) {gIndex++;}sIndex++;}return gIndex;
}
相关文章:

2023.2.14每日一题——455. 分发饼干
每日一题题目描述解题核心解法一:双指针题目描述 题目链接:455. 分发饼干 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],…...

MySQL入门篇-MySQL常用字符函数小结
备注:测试数据库版本为MySQL 8.0 这个blog我们来聊聊常见的字符函数 函数名函数用途UPPER()返回大写的字符LOWER()返回小写的字符LTRIM()左边去掉空格TRIM()去掉空格RTRIM()右边去掉空格SPACE()返回指定长度的空格CONCAT()连接字符串CONCAT_WS()指定分隔符连接字符串CHAR_LEN…...
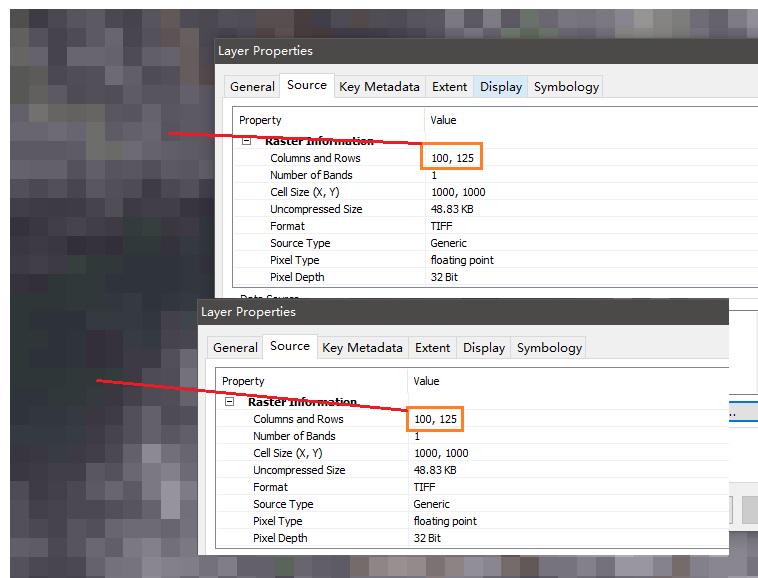
解决不同影像裁剪后栅格数据行列不一致问题
前言在处理栅格数据时,尽管用同一个矢量文件裁剪栅格数据,不同数据来源的栅格行列数也会出现不一致的情况。如果忽略或解决不好,会导致后续数据处理出现意想不到的误差或错误,尤其是利用编程实现数据处理时。因此,应当…...
visual studio2022配置opencv
标题:在vs下配置使用opencv 流程: 1、下载安装opencv 2、添加环境变量 3、vs中配置属性 4、使用 5、可能遇到的报错和解决 1、 下载安装opencv 官网下载地址: https://opencv.org/releases/ 我这里是windows环境,所以选择点击w…...

什么是销售管理?销售管理的五大职能
销售管理听起来很简单,似乎只是负责销售并确保客户满意,但事实上,它远不止于此。 销售管理的实际职能包括监督销售团队的工作,制定计划和设定目标,通常还包括确保销售流程的效率以获得最佳业务结果。 什么是销售管理…...

[CVPR‘22] EG3D: Efficient Geometry-aware 3D Generative Adversarial Networks
paper: https://nvlabs.github.io/eg3d/media/eg3d.pdfproject: EG3D: Efficient Geometry-aware 3D GANscode: GitHub - NVlabs/eg3d总结: 本文提出一种hybrid explicit-implicit 3D representation: tri-plane hybrid 3D representation,该方法不仅有…...

Learning C++ No.9【STL No.1】
引言: 北京时间:2023/2/13/18:29,开学正式上课第一天,直接上午一节思想政治,下午一节思想政治,生怕我们……,但,我深知该课的无聊,所以充分利用时间,把我的小…...
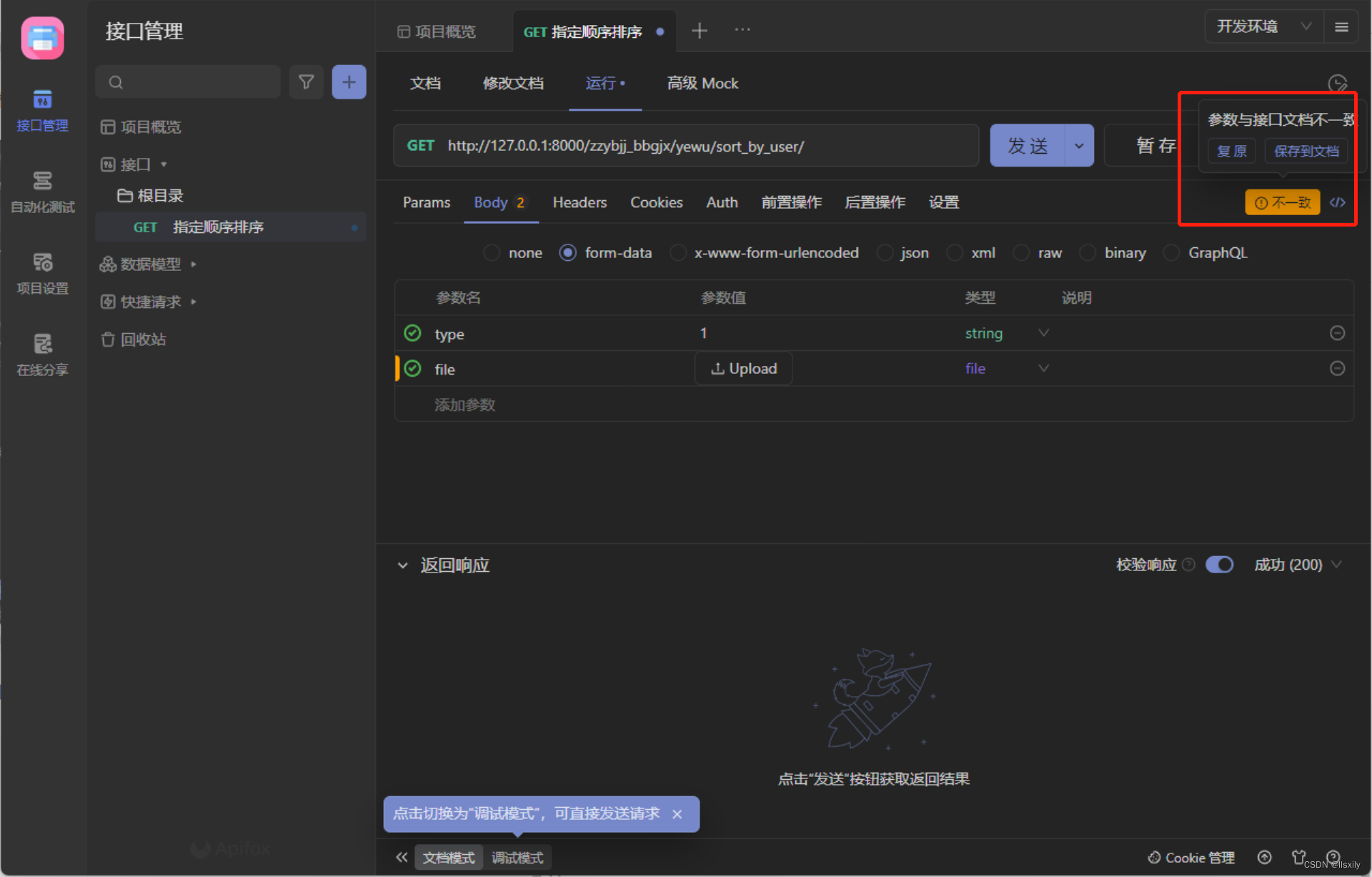
Apifox推荐-django后台验证token配置
最近事情很多,但是我还是想写一片推荐apifox的文章。 优秀的UI,清晰地逻辑,丰富的功能。对于我们这种业余选手来说,他真的很便利。 更新新版后有了更多贴心的功能,让你感觉他是一个有温度的工具。 最重要的是…...
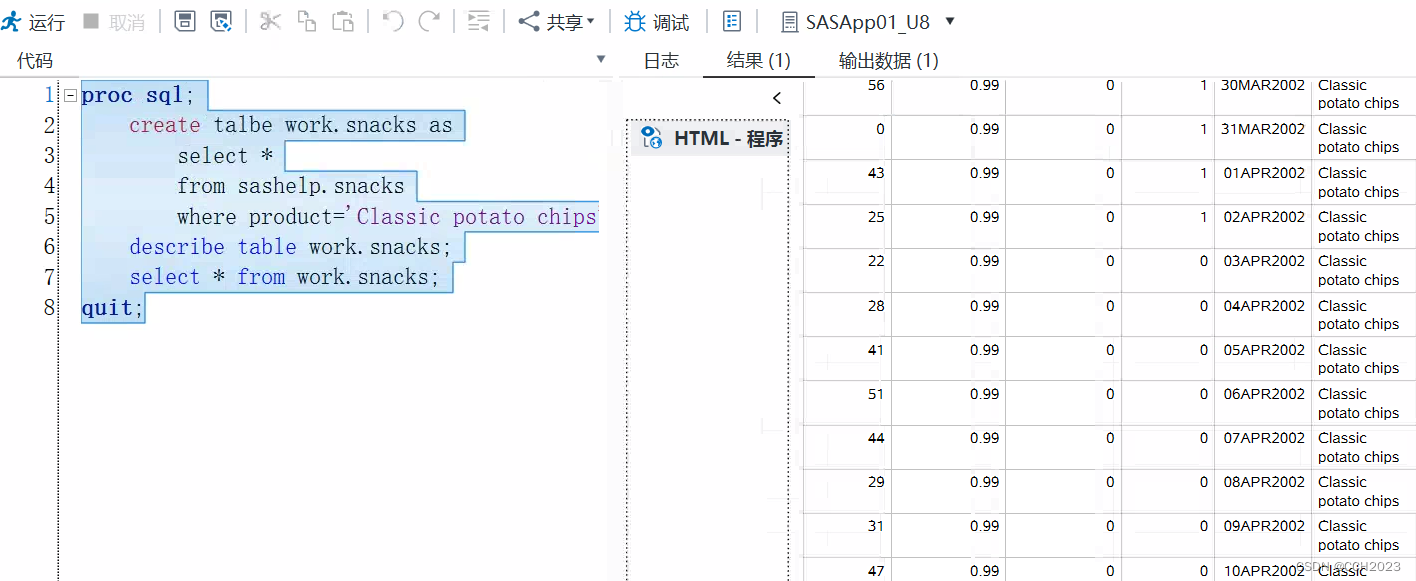
SAS应用入门学习笔记6
SQL (SAS): Features: 1)不需要在每个query中重复调用每个SQL; 2)每个statement都是独立去完成的; 3)我们是没有proc print和proc sort语句的;(order by) key synta…...

【3D目标检测】Pseudo-Stereo for Monocular 3D Object Detection in Autonomous Driving
目录概述细节背景与整体流程图像级别生成特征级别生成损失函数学习深度感知的特征概述 本文是基于单目图像的3D目标检测方法。 【2021】【MonoDLE】 研究的问题: 能否借助立体图像检测算法提高单目图像检测的效果如何实现右侧图像的生成 解决的方法: 受启发于伪…...

git 常用命令之 git branch
大家好,我是 17。 新建 git 分支 分支是并行开发的基础。分支名称的本质是对分支最后一个提交的引用。分支有多个,但 HEAD 只有一个,可以认为 HEAD 是"current branch"(当下的分支)。当你用git switch切换分支的时候,…...

Oracle数据泵
Oracle 数据泵:概览 作为一个基于服务器的用于高速移动数据与元数据的工具, Oracle 数据泵具有以下特点: •可通过 DBMS_DATAPUMP 调用 •可提供以下工具: – expdp – impdp – 基于 Web 的界面 •提供四种数据移动方法ÿ…...

ACWING寒假每日一题python
ACWING寒假每日一题 一、孤独的照片 一个点一个点的来看,比如对于GHGHG中间的G,找到他的左边的G,以及右边的G的位置,l,r分别等于1,答案就要多加上11 但是如果对于 GHHGHHG 中间的G,我们可以看到l,r等于2&a…...

御黑行动来袭--助力三月重保,构筑安全防线!
三月重保在即,重要网站及业务系统“零风险 零事故”是终极目标,作为业界网络安全实战派“老兵”--知道创宇将一如既往,为您提供重保期间“万无一失”的重要网站及业务系统防护。 值此三月重保的重要备战期,知道创宇推出由主力产品…...
)
JavaScript HTML DOM 元素 (节点)
HTML DOM 是指 HTML 文档对象模型,它是一种用于创建和处理 HTML 页面的标准 API。在 JavaScript 中,HTML DOM 可以被用来操作和修改网页的内容和结构。在本篇文章中,我们将详细探讨 JavaScript HTML DOM 元素 (节点)的作用以及在实际工作中的…...
mybatis-plus ---2
mybatis-plus插件 官网地址 分页插件 MyBatis Plus自带分页插件,只要简单的配置即可实现分页功能 配置并使用自带分页插件 Configuration MapperScan("com.itzhh.mapper")//可以将主类中的注解移到此处 public class MybatisPlusConfig {Beanpublic …...
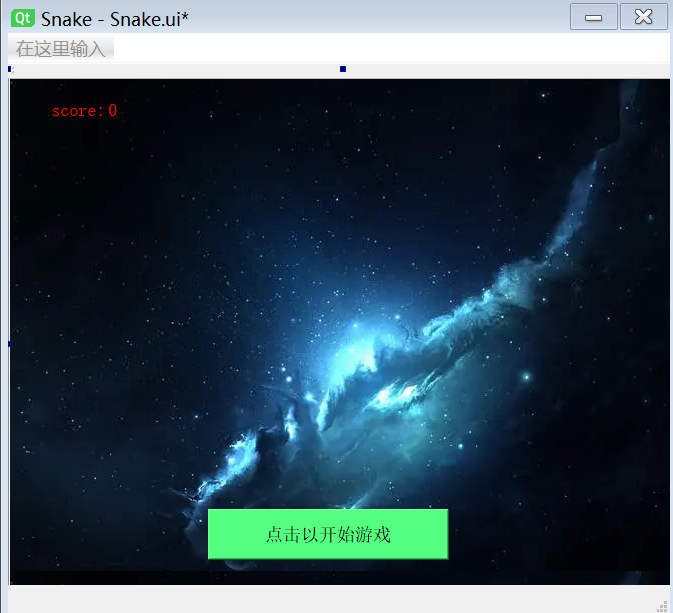
如何在Qt中设置背景图片,且不覆盖其它控件
正常情况,我们直接通过在样式表里设置背景图片会出现背景图片覆盖其它控件的情况,比如下面操作: 首先右击空白处,点击改变样式表。 然后选择background-image 然后点击铅笔图标 之后我们要先添加前缀,也就是我们…...

PMP考前冲刺2.14 | 2023新征程,一举拿证
承载2023新一年的好运让我们迈向PMP终点一起冲刺!一起拿证!每日5道PMP习题助大家上岸PMP!!!PMP项目管理题目1-2:1.公司了解到一个项目机会,领导让之前做过类似项目的项目经理报告一个粗略的成本…...
feign进行文件上传报错解决方案及有多个入参时的注意事项
一、情景回顾1、简单的文件上传的接口/*** 文件上传MultipartFile格式** param multipartFile 源文件* param filename 自定义文件名称,允许为空,为空时直接从源文件中拿* return*/RequestMapping("/uploadFileForMultipartFile")LogModuleAnn…...

java 枚举类型enum的用法详解
Java Enum原理 public enum Size{ SMALL, MEDIUM, LARGE, EXTRA_LARGE }; 实际上,这个声明定义的类型是一个类,它刚好有四个实例,在此尽量不要构造新对象。 因此,在比较两个枚举类型的值时,永远不需要调用equals方法…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
