第五十三章 DFS进阶(一)——剪枝优化
第五十四章 DFS进阶(一)——剪枝优化
- 一、什么是剪枝?
- 二、剪枝优化的策略
- 1、优化搜索顺序
- 2、排除等效冗余
- 3、可行性剪枝
- 4、最优性剪枝
- 5、记忆化搜索
- 三、例题
- 1、AcWing 165. 小猫爬山(DFS + 剪枝优化)
- 2、AcWing 167. 木棒(DFS + 剪枝优化)
- 3、AcWing 166. 数独(DFS + 剪枝优化 + lowbit函数 + 状态压缩)
一、什么是剪枝?
我们知道DFS在很多场景内都是一个指数级别的算法,其时间复杂度是相当巨大的。
而在我们枚举的时候,有很多种情况在枚举了一部分之后,就知道它不是正确答案了,那么在这种情况下,该种情况就没有继续向后枚举的必要了。那么将这些情况挑出来并舍弃掉的过程,就叫做剪枝。它能在一定程度上,对我们的代码进行优化。
二、剪枝优化的策略
1、优化搜索顺序
我们搜索的过程其实就是一个暴力枚举所有情况的过程,而之所以这么多情况,关键在于我们的选择太多。
那么为了减少搜索的时间,我们就要尽可能地减少一些选择。这就是我们优化搜索顺序的目的。
比如说,给定一串正整数,我们要找到几个数字的组合,不超过给定的最大值M。
假设我们这的数字是从小到大排列的,如果一开始就选一个最小的数字的话,那么我们后续的选择就会很多,这就导致我们的搜索树的子树很多,就导致节点变多,从而加长了时间。
但是我们从大到小开始枚举的话,由于这些数字很大,那么留给后续数字的可选择的空间就会变少,从而减少了选择,即优化了时间。
2、排除等效冗余
等效冗余即虽然方案和方案之间的选择不同,但是他们导致的结果是一致的,在这种情况下,我们只需要选择一种即可。比如刚刚的例题,我们只在乎选出一个组合,但是组合之间的顺序其实是无关紧要的,那么我们只需要枚举出一种顺序,其他的扔掉就行了。
3、可行性剪枝
依旧以刚刚的问题为例子,如果某种方案在枚举过程中已经超过了最大值M,那么后续就不需要枚举了,因为这种方案肯定不行。
4、最优性剪枝
如果当前方案通过某种判断已经确定不是最优解了,那么也可以直接扔掉。
5、记忆化搜索
三、例题
1、AcWing 165. 小猫爬山(DFS + 剪枝优化)
AcWing 165. 小猫爬山(DFS + 剪枝优化)
#include<bits/stdc++.h>
using namespace std;
const int N = 20;
typedef long long ll;
int n, w;
int c[N];
int ans = N;
bool st[N];
ll sw[N];
bool cmp(int x, int y)
{return x >y;
}
void dfs(int u, int nums)
{if(u == n){ans = min(ans, nums);return;}if(nums >= ans)return;int cnt = 0;for(int i = 1; sw[i] != 0; i ++ ){if(sw[i] + c[u] <= w){sw[i] += c[u];dfs(u + 1, nums);sw[i] -= c[u];}cnt ++;}sw[cnt + 1] = c[u];dfs(u + 1, cnt + 1);sw[cnt + 1] -= c[u];
}void solve()
{cin >> n >> w;for(int i = 0; i < n; i ++ )cin >> c[i];sort(c, c + n, cmp);dfs(0, 0);cout << ans << endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();return 0;
}2、AcWing 167. 木棒(DFS + 剪枝优化)
AcWing 167. 木棒(DFS + 剪枝优化)
#include<bits/stdc++.h>
using namespace std;
const int N = 70;int n;
int w[N];
int sum, length;
bool st[N];bool dfs(int u, int cur, int start)
{if (u * length == sum) return true;if (cur == length) return dfs(u + 1, 0, 0);for (int i = start; i < n; i ++ ){if (st[i] || cur + w[i] > length) continue;st[i] = true;if (dfs(u, cur + w[i], i + 1)) return true;st[i] = false;if (!cur || cur + w[i] == length) return false;int j = i;while (j < n && w[j] == w[i]) j ++ ;i = j - 1;}return false;
}int main()
{while (cin >> n, n){memset(st, 0, sizeof st);sum = 0;for (int i = 0; i < n; i ++ ){cin >> w[i];sum += w[i];}sort(w, w + n);reverse(w, w + n);length = 1;while (true){if (sum % length == 0 && dfs(0, 0, 0)){cout << length << endl;break;}length ++ ;}}return 0;
}3、AcWing 166. 数独(DFS + 剪枝优化 + lowbit函数 + 状态压缩)
AcWing 166. 数独(DFS + 剪枝优化 + lowbit函数 + 状态压缩)
#include<bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 9;
int row[N], col[N], ones[1 << N], cell[3][3];
char str[100];
int ma[1 << N];
int lowbit(int x)
{return x & -x;
}int get(int x, int y)
{return row[x] & col[y] & cell[x / 3][y / 3];
}void init()
{for(int i = 0; i < N; i ++ )row[i] = col[i] = (1 << N) - 1;for(int i = 0; i < 3; i ++ )for(int j = 0; j < 3; j ++ )cell[i][j] = (1 << N) - 1;
}void draw(int x, int y, int nums, bool flag)
{if(flag)str[x * N + y] = '1' + nums;elsestr[x * N + y] = '.';int v = 1 << nums;if(!flag)v = -v;row[x] -= v;col[y] -= v;cell[x / 3][y / 3] -= v;
}bool dfs(int cnt)
{if(!cnt)return true;int minv = INF;int x, y;for(int i = 0; i < N; i ++ ){for(int j = 0; j < N; j ++ ){if(str[i * N + j] == '.'){//看看这个格子能写哪几个数字。int state = get(i, j);//看看能写几个数,我们从情况小的开始枚举,目的是优化。if(ones[state] < minv){minv = ones[state];x = i, y = j;}} }}int state = get(x, y);for(int i = state; i ; i -= lowbit(i)){//枚举当前所有可以写的数字int t = ma[lowbit(i)];//在该位补上合适的数字,并更新行,列,九宫格的状态draw(x, y, t, true);if(dfs(cnt - 1))return true;//复原draw(x, y, t, false);} return false;
}void solve()
{for(int i = 0; i < N; i ++ )ma[1 << i] = i;//记录1 << i代表的是哪个数字for(int i = 0; i < 1 << N; i ++ )for(int j = 0; j < N; j ++ )ones[i] += i >> j & 1;//记录二进制数字中1的个数while(cin >> str, str[0] != 'e'){init();int cnt = 0;//记录需要我们写的格子的数目for(int i = 0, k = 0; i < N; i ++ )for(int j = 0; j < N; j ++, k ++ ){if(str[k] != '.'){int t = str[k] - '1';draw(i, j, t, true);}elsecnt ++;}dfs(cnt);cout << str << endl; }}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();
}相关文章:
——剪枝优化)
第五十三章 DFS进阶(一)——剪枝优化
第五十四章 DFS进阶(一)——剪枝优化一、什么是剪枝?二、剪枝优化的策略1、优化搜索顺序2、排除等效冗余3、可行性剪枝4、最优性剪枝5、记忆化搜索三、例题1、AcWing 165. 小猫爬山(DFS 剪枝优化)2、AcWing 167. 木棒…...
Java字节码深度知多少?
文章目录1、字节码结构1.1、基本结构1.2、实际观测2、内存表示3、方法调用指令4、invokedynamicEND结语Java真的是长盛不衰,拥有顽强的生命力。其中,字节码机制功不可没。字节码,就像是 Linux 的 ELF。有了它,JVM直接摇身一变&…...

【C++】智能指针(万字详解)
🌈欢迎来到C专栏~~智能指针 (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort目前状态:大三非科班啃C中🌍博客主页:张小姐的猫~江湖背景快上车🚘,握好方向盘跟我有一起打天下嘞!送给自己的一句鸡汤&…...
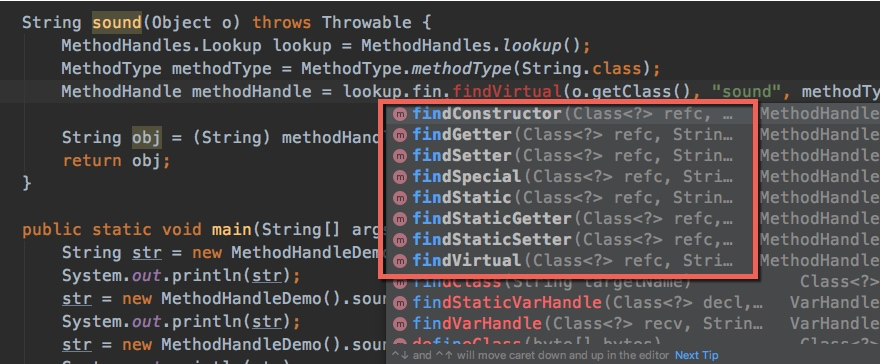
使用docker配置mysql主从复制
1.新建主服务器容器实例: docker run -p 3307:3306 --name mysql \ -v /docker/mysql/data:/var/lib/mysql \ -v /docker/mysql/conf:/etc/mysql/conf \ -v /docker/mysql/log:/var/log/mysql \ -e MYSQL_ROOT_PASSWORDroot \ -d mysql:5.7 设置容器卷之后…...

v3 异步组件及分包使用
1 app.vue <template> <!-- vue3异步组件必须使用suspense --> <Suspense> <template #default> <!-- 异步组件 --> <SyncVue></SyncVue> </template> <template v-slot:fallback> <!-- 优先显示骨架屏 --> <…...

实用调试技巧【上篇】
🔴本文章是在 Visual Studio 2022(VS2022)编译环境下进行操作讲解 文章目录🥳1. 什么是bug?🥳2.调试有多重要?2.1. 我们是如何写代码的?2.2.调试是什么?2.3.调试的基本步…...

JavaScript 教程
手册简介JavaScript 是世界上最流行的脚本语言。 JavaScript 是属于 web 的语言,它适用于 PC、笔记本电脑、平板电脑和移动电话。 JavaScript 被设计为向 HTML 页面增加交互性。 许多 HTML 开发者都不是程序员,但是 JavaScript 却拥有非常简单的语法。几…...

在SpringBoot里面使用原生的Servlet
在SpringBoot里面使用Servlet 首先在主程序中添加注解主程序添加ServletComponentScan // 加上这个注解之后就可以使用原生的组件了 HttpServlet 继承HttpServlet 重写方法 添加WebServlet 第一种方式使用注解 WebServlet(value "/helsk") public class HelloSe…...

商标被驳回,先别慌!挽回商标有办法
商标注册是一个漫长的等待过程,提交了注册申请之后不代表就能得心应手。商标局在接收到申请后,便会开始各阶段审查,面对不符合条件的商标会予以商标驳回。商标局基于什么原因而驳回注册申请呢?驳回后还有必要进行商标驳回复审吗?今天心周企…...
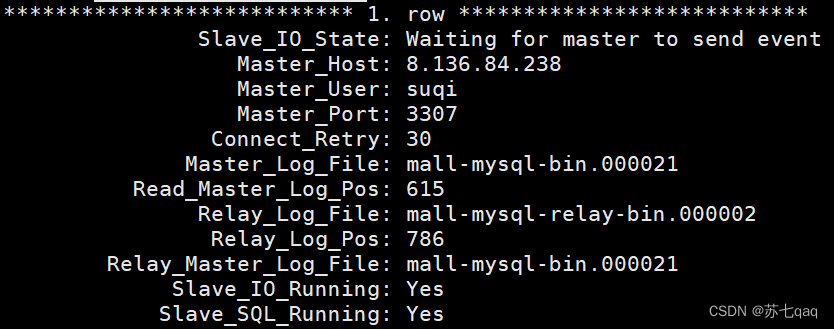
VMware安装Linux虚拟机后忘记root密码处理方法
OS版本:Red Hat 7.7 问题说明: 之前用VMWare安装了一台Linux虚机,由于长期没使用,导致忘记了root密码。所以需要修改root密码。 Root密码修改 现将修改root密码的操作步骤记录如下。 1.启动虚拟机,出现启动倒计时…...
Centos安装OpenResty
文章目录一. OpenResty是什么二. OpenResty的安装1. 安装开发库2. 安装OpenResty仓库3. 安装OpenResty4. 安装opm工具5. 目录结构6. 配置nginx的环境变量7. 启动和运行8. 配置文件修改三. 小案例1. 案例说明2. OpenResty监听请求3. 编写业务代码4. 获取请求参数一. OpenResty是…...
阿里云部署SpringBoot项目
目录 步骤1:购买服务器(新用户免费试用一个月) 步骤2:查看服务器相关信息 编辑 步骤3:设置安全组 步骤4:远程连接 步骤5:使用FinalShell连接阿里云服务器 步骤6:阿里云服务器上安装JDK 编辑 步骤7…...

EdgeCOM嵌入式边缘计算机的参数配置
EdgeCOM嵌入式边缘计算机的参数配置: 下面以 eth0 为例进行命令说明。 在 Linux 系统下,使用 ifconfig 命令可以显示或配置网络设备,使用 ethtool 查询及 设置网卡参数。 设置 IP 地址,查看当前网卡详情: rootfl-imx6u…...
字节软件测试岗:惨不忍睹的三面,幸好做足了准备,月薪15k,拿到offer
我今年25岁,专业是电子信息工程本科,19年年末的时候去面试,统一投了测试的岗位,软件硬件都有,那时候面试的两家公司都是做培训的,当初没啥钱,他们以面试为谎言再推荐去培训这点让我特别难受。 …...
【编程基础之Python】5、安装Python第三方模块
【编程基础之Python】5、安装Python第三方模块安装Python第三方模块为什么需要安装第三方模块Python包管理器介绍pippip installpython -m pip installcondaconda install在Windows环境中安装Python模块安装numpy安装pandas安装matplotlib在Linux环境中安装Python模块在PyCharm…...

JavaScript 教程导读
JavaScript 是 Web 的编程语言。所有现代的 HTML 页面都使用 JavaScript,可以用于改进设计、验证表单、检测浏览器、创建cookies等。JavaScript 非常容易学。本教程将教你学习从初级到高级JavaScript知识。JavaScript 在线实例本教程包含了大量的 JavaScript 实例&a…...

BigDecimal
文章目录1. BigDecimal 的舍入模式(RoundingMode)1.1 ROUND_UP1.2 ROUND_DOWN1.3 ROUND_HALF_UP1.4 ROUND_HALF_DOWN1.5 ROUND_CEILING1.6 ROUND_FLOOR1.7 ROUND_HALF_EVEN1.8 ROUND_UNNECESSARY2. BigDecimal的运算——加减乘除2.1 加法 add()函数 减法…...

代码随想录【Day15】|102. 二叉树的层序遍历、226. 翻转二叉树、101. 对称二叉树
102. 二叉树的层序遍历 题目链接 题目描述: 给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。 难点: 思路: 需要借用一个辅助数据结构即队列来实现…...

Python学习笔记:快速上手:基础知识
快速上手:基础知识 数和表达式 除法 >>> 1 / 2 0.5 >>> 1 / 1 1.0整除 >>> 1 // 2 0 >>> 1 // 1 1 >>> 5.0 // 2.4 2.0求余(求模): x % y 等价于x - ((x // y) * y)。 …...

excel学习笔记-导入外部文件,报错,数值格式变换,日期格式的转化,求和快捷键,冻结窗格
这里写目录标题一、导入外部文件1.导入csv文件2.导入txt文件3.修改txt内容,需要刷新才能看见更改二、报错三、数值格式变换四、日期格式的转化五、ALT ,求和快捷键六、冻结窗格一、导入外部文件 1.导入csv文件 2.导入txt文件 3.修改txt内容,…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...
