算法训练营DAY51|300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组
本期是求子序列的新的一期,题目前两道有一些相似之处,思路差不多,第三道有一点难度,但并不意味着第一道没有难度,没有做过该类型题的选手,并不容易解出题解。
300. 最长递增子序列 - 力扣(LeetCode)![]() https://leetcode.cn/problems/longest-increasing-subsequence/
https://leetcode.cn/problems/longest-increasing-subsequence/
题目大意是给一个数组,要求返回最长的递增的序列,题目要求是删除中间一些元素,或者不删除也可以,返回最长的递增的数组长度,又是一道这种题目,如果你是之前做过类似题目大意的朋友应该知道,通常来说要求可以删除中间元素的,通常我们都不是真的删除数据,而是通过遍历来间接的实现删除中间的数据的过程,换句话来说,不是真正删除数据,而是要删除的数据我们不处理它。
dp数组的含义:dp【i】代表到该位置为止,i之前包括i的最长的递增子序列是多大。但是需要注意的是,整体的最长的递增子序列,可不一定是dp数组的最后一个数据,因为很可能,我们要找的最长递增序列结尾在前面就已经出现了,而遍历到数组最后一个位置,可能只是不同的递增子序列路线,不一定是长的。
递推公式:由于递增子序列,很有可能不是连续的,需要删除部分数据,那么我们如何实现这一部分的代码呢?答案是用两个循环,一个是外层循环控制遍历到数组中的哪一个位置了,另一个内层循环是重复遍历从起始位置到i这个位置,如果出现前面的0-i的数据比当前遍历到的数小,那么递增子序列长度+1,这也就是相当于不符合条件的数据我们直接略过去,符合条件的再使长度+1,间接的删除了多余数据
也就是if(nums【j】< nums【i】)dp【i】=max(dp【i】,dp【j】+1)
取最大值,看看它原本的大还是遍历完的最长递增子序列长度大。每次j都会从头开始遍历一次,看看这回多出来的那个数据是否能使子序列长度增加。
dp数组初始化:dp数组的初始化都是初始化为1,这是因为如果只有一个数据的话,那么最长递增子序列肯定是1,不可能返回0,而其他的为什么也初始化为1呢?因为如果出现大于1的递增子序列长度那么就一定会被递推公式所覆盖,所以我们都初始化为1。
遍历顺序:都是从前向后遍历,不用多说。
class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int>dp(nums.size(),1);int result=1;for(int i=1;i<nums.size();i++){for(int j=0;j<i;j++){if(nums[i]>nums[j])dp[i]=max(dp[i],dp[j]+1);}if(result<dp[i])result=dp[i];}return result;}
};代码中的result的用处就是,记录最长的递增子序列有多长,然后最后返回它。
674. 最长连续递增序列 - 力扣(LeetCode)![]() https://leetcode.cn/problems/longest-continuous-increasing-subsequence/这道题和上一道题很像,只不过这道题我们要求的是连续的递增子序列了,连续的递增子序列,我个人认为要比非连续的要好写,或者说好想一点。
https://leetcode.cn/problems/longest-continuous-increasing-subsequence/这道题和上一道题很像,只不过这道题我们要求的是连续的递增子序列了,连续的递增子序列,我个人认为要比非连续的要好写,或者说好想一点。
dp数组含义:dp数组的含义和上一道题一样,也是到该位置为止,i之前包括i的最长的连续递增子序列是多长,但是我觉得这种含义太抽象了,不利于初学者理解,我认为可以将这句话翻译为以i结尾的这条递增序列有多长,这其实也就间接的证明了我们之前所说的含义,即最后一个下标的dp数组所代表的数据,并不一定是最大的。因为它代表的应该是以i为结尾的这条递增序列最长有多长。
递推公式:由于是连续的最长递增序列,所以我们只看是否是连续递增就可以了,那么连续就体现在上一个数字和这一个数字的比较
if(nums【i】==nums【i-1】)dp【i】=dp【i-1】+1;
dp数组初始化和遍历顺序都和上一道题一样,不做赘述。
class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {vector<int>dp(nums.size(),1);int result=1;for(int i=1;i<nums.size();i++){if(nums[i]>nums[i-1])dp[i]=dp[i-1]+1;result=max(result,dp[i]);}return result;}
};718. 最长重复子数组 - 力扣(LeetCode)![]() https://leetcode.cn/problems/maximum-length-of-repeated-subarray/这道题是略有难度的一道题,为什么说它略有难度呢?并不是递推公式有多难理解,而是dp数组的的表示,要清楚的想到有一些难度。
https://leetcode.cn/problems/maximum-length-of-repeated-subarray/这道题是略有难度的一道题,为什么说它略有难度呢?并不是递推公式有多难理解,而是dp数组的的表示,要清楚的想到有一些难度。
dp数组的含义:这是给我们两个数组,然后让我们求重复的连续部分最长有多长,这是我们就需要使用二维数组来表示了,其中一维表示一个数组,另一维表示另一数组,而dp【i】【j】表示的是第一个数组的i-1位置,下标对应的第二个数组的j-1下标位置,最长的重复子数组有多长,那么为什么我们要表示i-1和j-1呢?直接表示i和j不好吗?这样定义是为了方便dp数组的初始化,在下面还有对此处的详解。
递推公式:从哪个方向上能够推出dp【i】【j】呢?当数组1的i-1下标位置的数字和数组2下标为j-1的位置数字相等的时候,不就是说明两数组有一数字重复吗,此时就是长度+1,那么递推公式就理所当然的是if(nums1【i-1】==nums2【j-1】)dp【i】【j】=dp【i-1】【j-1】+1;
就是上一个长度再加上这回匹配成功的长度1。
dp数组的初始化:看到这里相信大家可能已经带有一些疑问了,这样定义dp数组那么当遍历到i和j等于0的时候,不就出问题了吗?这也正是初始化所要解决的问题,正是因为我们这样定义dp数组导致了当i和j其中一个为0时候,是非法的,所以我们初始化第一行和第一列时候全部初始化为0,其余部分因为有递推公式的存在,每个位置是依靠前一个位置的值,所以i和j非0部分初始化为什么都可以。那么为什么我们要这样定义数组呢?因为如果dp【i】【j】就是表示它处在i和j的位置上时候有多长,这会导致初始化i和j其一等于0时,也就是二维数组的第一行和第一列可能不全为0,这会增大初始化的代码强度,可能第一个数组i==0的时候第二个数组的j对应某位置两数组有数据相等,也就是第一行某处有位置应该初始化为1,讲到这里大家反复揣摩一下,用笔画一下,可能就明白了。
遍历顺序:遍历顺序还是从前向后,两个for循环,分别遍历第一个数组和第二个数组,从前向后查看是否有相等的元素出现。
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>>dp(nums1.size()+1,vector<int>(nums2.size()+1,0));int result=0;for(int i=1;i<=nums1.size();i++){for(int j=1;j<=nums2.size();j++){if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1;result=max(result,dp[i][j]);}}return result;}
};以上就是本章的全部内容,子序列问题起初做都没有什么思路,要勤加练习思维,才能够想出用动态规划解决问题的思路。
相关文章:
算法训练营DAY51|300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组
本期是求子序列的新的一期,题目前两道有一些相似之处,思路差不多,第三道有一点难度,但并不意味着第一道没有难度,没有做过该类型题的选手,并不容易解出题解。 300. 最长递增子序列 - 力扣(Leet…...
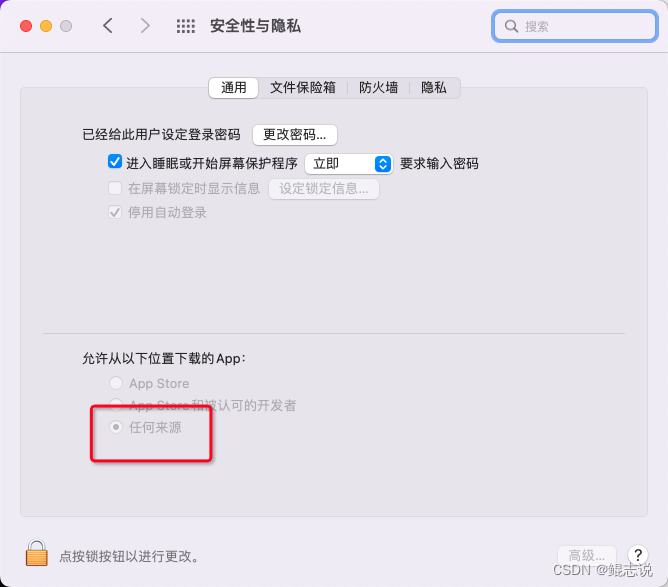
mac:彻底解决-安装应用后提示:无法打开“XXX”,因为无法验证开发者的问题;无法验证此App不包含恶意软件
mac从浏览器或其他电脑接收了应用,但是打开报错 目录报错解决办法一次性方法永久解决方法验证恢复应用验证报错 截图如下: 错误信息 无法打开“XXX”,因为无法验证开发者的问题;无法验证此App不包含恶意软件 解决办法 一次性方…...

CPU 指标 user/idle/system 说明
从图中看出,一共有五个关于CPU的指标。分别如下: User User表示:CPU一共花了多少比例的时间运行在用户态空间或者说是用户进程(running user space processes)。典型的用户态空间程序有:Shells、数据库、web服务器…… Nice N…...
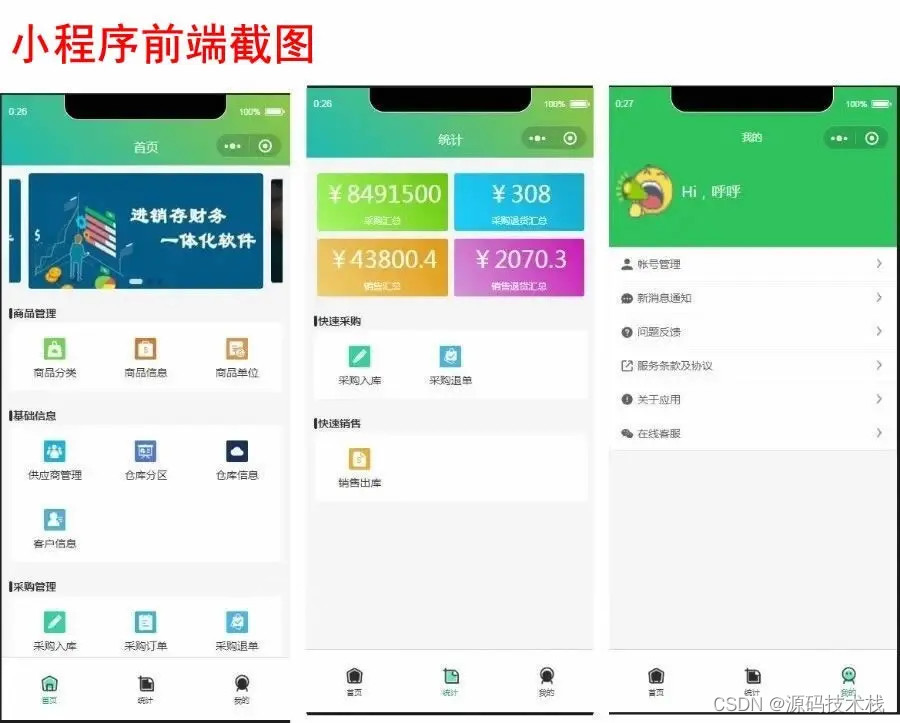
Thinkphp大型进销存ERP源码/ 进销存APP源码/小程序ERP系统/含VUE源码支持二次开发
框架:ThinkPHP5.0.24 uniapp 包含:服务端php全套开源源码,uniapp前端全套开源源码(可发布H5/android/iod/微信小程序/抖音小程序/支付宝/百度小程序) 注:这个是全开源,随便你怎么开,怎么来&a…...
hgame2023 WebMisc
文章目录Webweek1Classic Childhood GameBecome A MemberGuess Who I AmShow Me Your BeautyWeek2Git Leakagev2boardSearch CommodityDesignerweek3Login To Get My GiftPing To The HostGopher Shopweek4Shared DiaryTell MeMiscweek1Where am I神秘的海报week2Tetris Master…...

67. Python的绝对路径
67. Python的绝对路径 文章目录67. Python的绝对路径1. 准备工作2. 路径3. 绝对路径3.1 概念3.2 查看绝对路径的方法4. 课堂练习5. 用绝对路径读取txt文件6. 加\改写绝对路径6.1 转义字符知识回顾6.2 转义字符改写7. 总结1. 准备工作 对照下图,新建文件夹和txt文件…...

VHDL语言基础-组合逻辑电路-加法器
目录 加法器的设计: 半加器: 全加器: 加法器的模块化: 四位串行进位全加器的设计: 四位并行进位全加器: 串行进位与并行进位加法器性能比较: 8位加法器的实现: 加法器的设计&…...

内存检测工具Dr.Memory在Windows上的使用
之前在https://blog.csdn.net/fengbingchun/article/details/51626705 中介绍过Dr.Memory,那时在Windows上还不支持x64,最新的版本对x64已有了支持,这里再总结下。 Dr.Memory源码地址https://github.com/DynamoRIO/drmemory,最新发…...

J6412四网口迷你主机折腾虚拟机教程
今天给大家做一个四网口迷你主机折腾虚拟机的安装教程,主机采用的是maxtang大唐NUC J6412 intel i226V四网口的迷你主机,这款主机它是不能直接装上NAS的,必须使用虚拟机系统,近期研究了下然后做了一个教程分享给大家。 首先需要做…...

电子招标采购系统—企业战略布局下的采购寻源
智慧寻源 多策略、多场景寻源,多种看板让寻源过程全程可监控,根据不同采购场景,采取不同寻源策略, 实现采购寻源线上化管控;同时支持公域和私域寻源。 询价比价 全程线上询比价,信息公开透明ÿ…...

elasticsearch 之 mapping 映射
当我们往 es 中插入数据时,若索引不存在则会自动创建,mapping 使用默认的;但是有时默认的映射关系不能满足我们的要求,我们可以自定义 mapping 映射关系。 mapping 即索引结构,可以看做是数据库中的表结构,…...
)
2023年rabbitMq面试题汇总2(5道)
一、如何确保消息接收⽅消费了消息?接收⽅消息确认机制:消费者接收每⼀条消息后都必须进⾏确认(消息接收和消息确认是两个不同操作)。只有消费者确认了消息,RabbitMQ才能安全地把消息从队列中删除。这⾥并没有⽤到超时…...
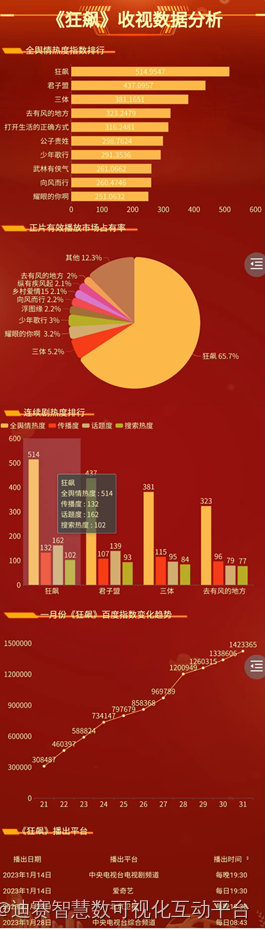
电视剧《狂飙》数据分析,正片有效播放市场占有率达65.7%
哈喽大家好,春节已经过去了,朋友们也都陆陆续续开工了,小编在这里祝大家开工大吉!春节期间,一大批电视剧和网剧上映播出,其中电视剧《狂飙》以不可阻挡之势成功成为“开年剧王”。这里小编整理了一些《狂飙…...

cas单点登录后重定向次数过多问题以及调试cas-dot-net-client
问题描述: web项目应用cas作为单点登录站点,登录后无法打开WEB项目的页面,报错,说重定向次数过多。 老实说,这种问题,以前遇到过不少,是我这种半桶水程序员的噩梦。解决这种问题,不…...
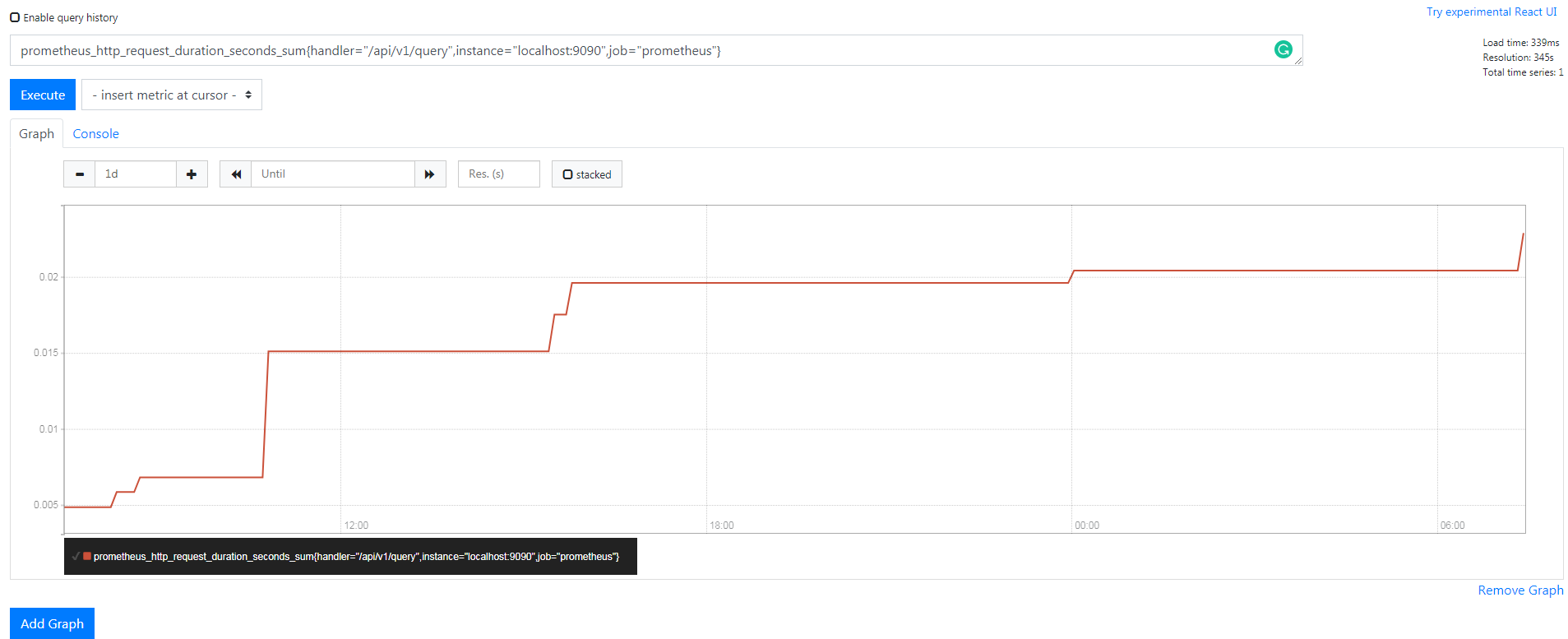
【监控】Prometheus(普罗米修斯)监控概述
文章目录一、监控系统概论二、基础资源监控2.1、网络监控2.2、存储监控2.3、服务器监控2.4、中间件监控2.5、应用程序监控(APM)三、Prometheus 简介3.1、什么是 Prometheus3.2、优点3.3、组件3.4、架构3.5、适用于什么场景3.6、不适合什么场景四、数据模…...
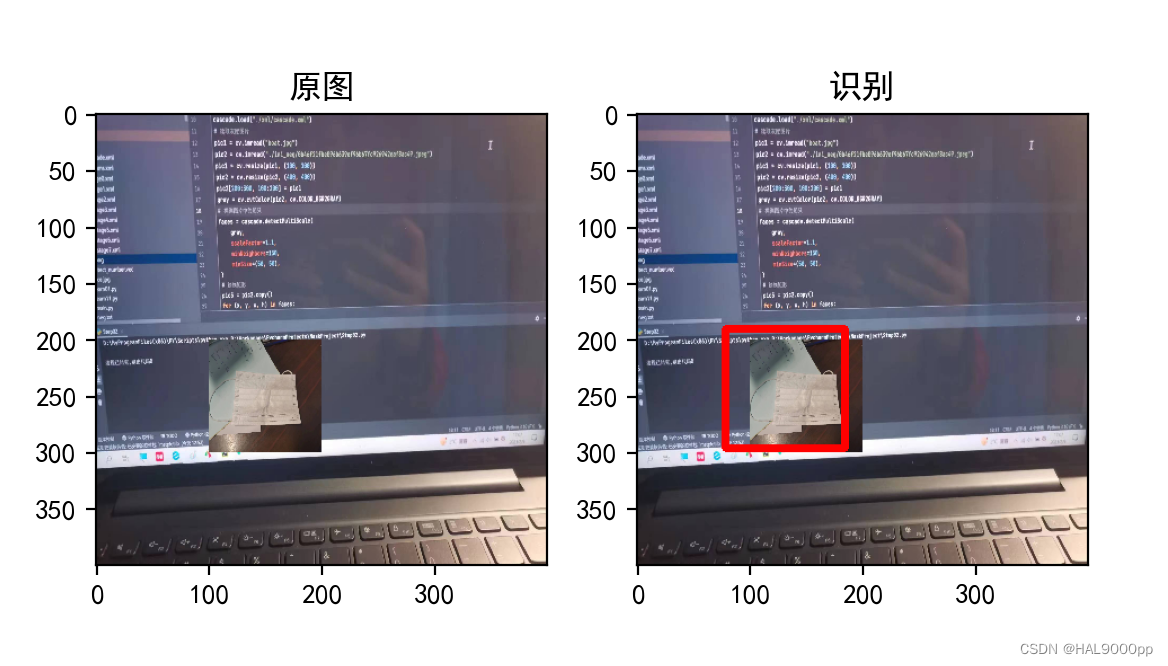
opencv+python物体检测【03-模仿学习】
仿照练习:原文链接 步骤一:准备图片 正样本集:正样本集为包含“识别物体”的灰度图,一般大于等于2000张,尺寸不能太大,尺寸太大会导致训练时间过长。 负样本集:负样本集为不含“识别物体”的…...

计算机科学基础知识第二节讲义
课程链接 运行环境:WSL Ubuntu OMZ终端 PS:看到老师终端具有高亮和自动补全功能,我连夜肝出oh-my-zsh安装教程,实现了此功能。 这节课主要讲变量的语法、控制流程、shell功能等内容。 修改终端用户名,输入密码后重启…...

openssl genrsa 命令详解
文章目录一、openssl genrsa 命令介绍二、openssl genrsa 命令的语法及选项三、实例1、生成512位的 RSA 秘钥,输出到屏幕。2、生成512位 RSA 私钥,输出到指定的文件 genrsa.txt3、生成 1024 位 RSA 秘钥,采用 des 算法加密,加密密…...
、C99、C11、C17、C2X)
C语言标准 —— C89(C90)、C99、C11、C17、C2X
C语言主要的三个标准:C89(C90)、C99、C11、K&R C 指的是 C 语言的原始版本。1978年,C 语言的发明者丹尼斯里奇(Dennis Ritchie)和布莱恩柯林(Brian Kernighan)合写了一本…...

基于Java+Dubbo设计的智能公交查询系统
一、项目背景 随着经济的飞速发展,人们的生活质量有了较大的提高,城市居民的出行变得越来越频繁,城市交通也面临越来越多的挑战。城市公共交通具有客流量大、成本低、效率高、节约资源等优势,因此,如何大力发展公交产业,鼓励人们乘坐公交出行,进而改善交通状况,是一个值得思考…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
