操作系统(day09) -- 连续分配管理方式
连续分配管理方式
单元连续分配
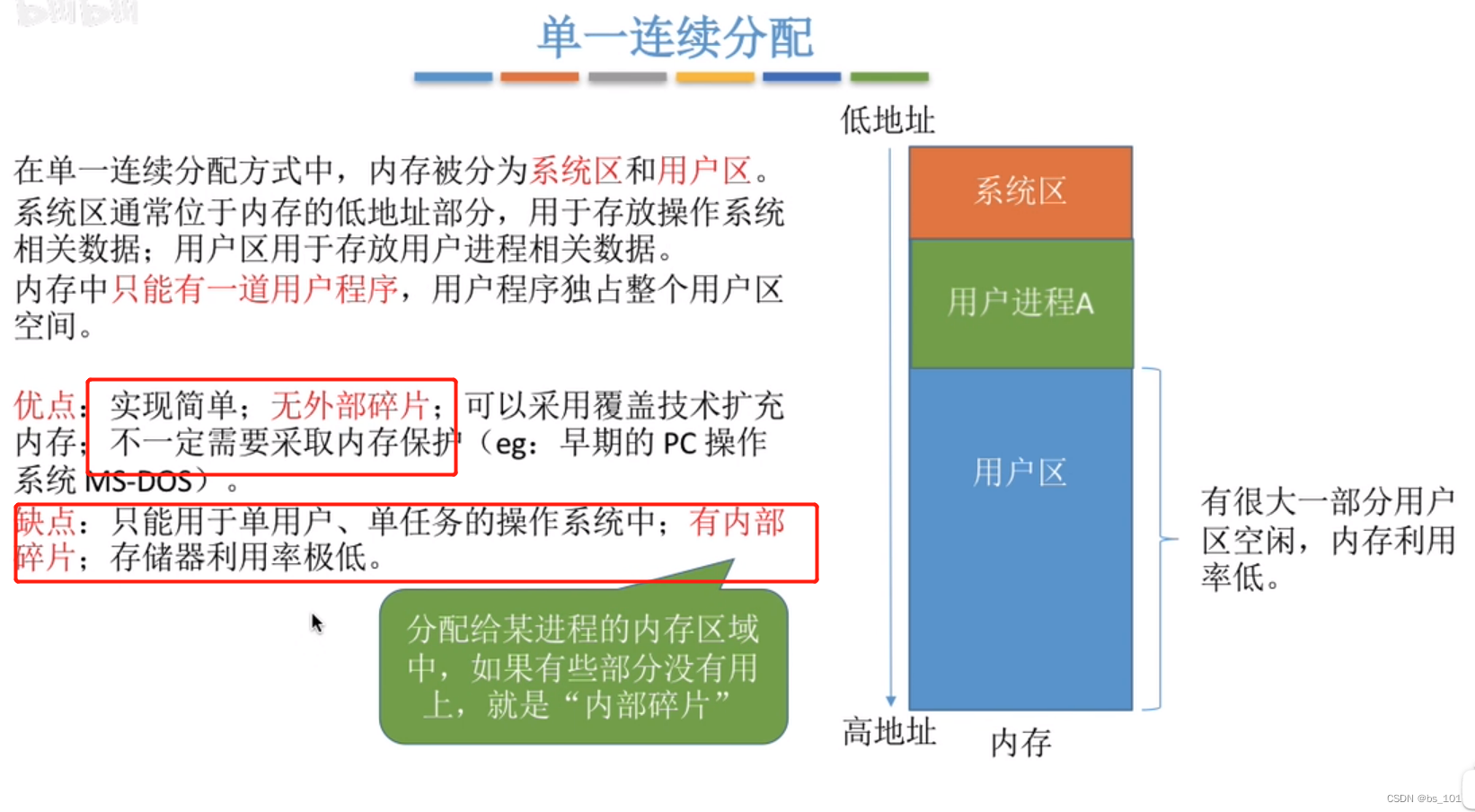
动态分区分配
1.系统要用什么样的数据结构记录内存的使用情况？
两种常用的数据结构
- 空闲分区表
每个空闲分区对应一个表项。表项中包含分区号、分区大小、分区起始地址等信息 - 空闲分区链
每个分区的起始部分和末尾部分分别设置前向指针和后向指针。起始部分出还可记录分区大小等信息
2.当很多个空闲分区都能满足需求时，应该选择哪个分区进行分配？
引出动态分区分配算法
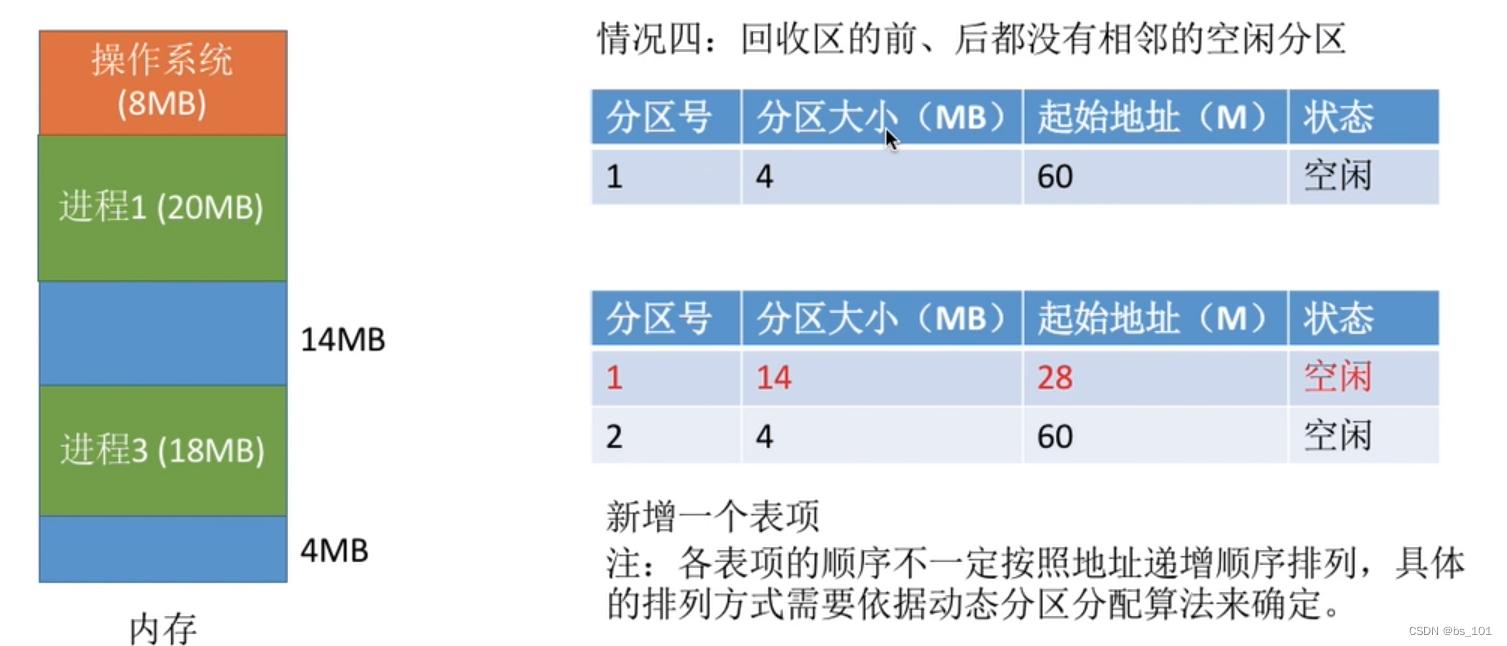
3.如何进行分区的分配回收操作？假设系统采用的数据结构是“空闲分区表”
- 回收区前有相邻的空闲分区
- 回收区后有相邻的空闲分区
- 回收前、后各有一个相邻的空闲分区
- 回收前、后都没有相邻的空闲分区
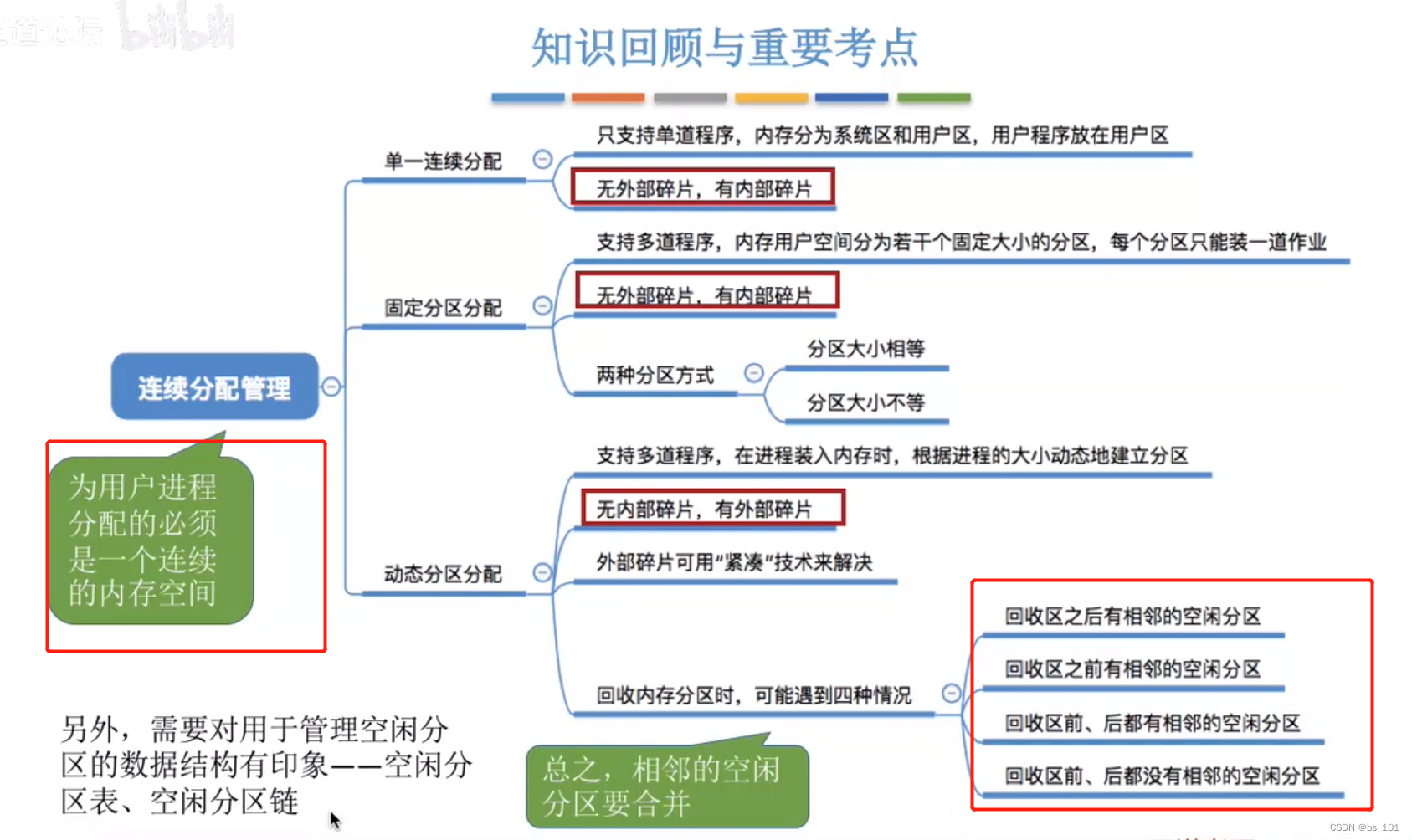
课后思维导图总结
动态分区分配算法
首次适应算法
每次都从低地址开始查找，找到第一个能满足大小的空闲分区。
如何实现？
空闲分区以地址递增的次序排列。每次分配内存时顺序查找空闲分区链（或空闲分区表），找到大小能满足要求的第一个空闲分区。
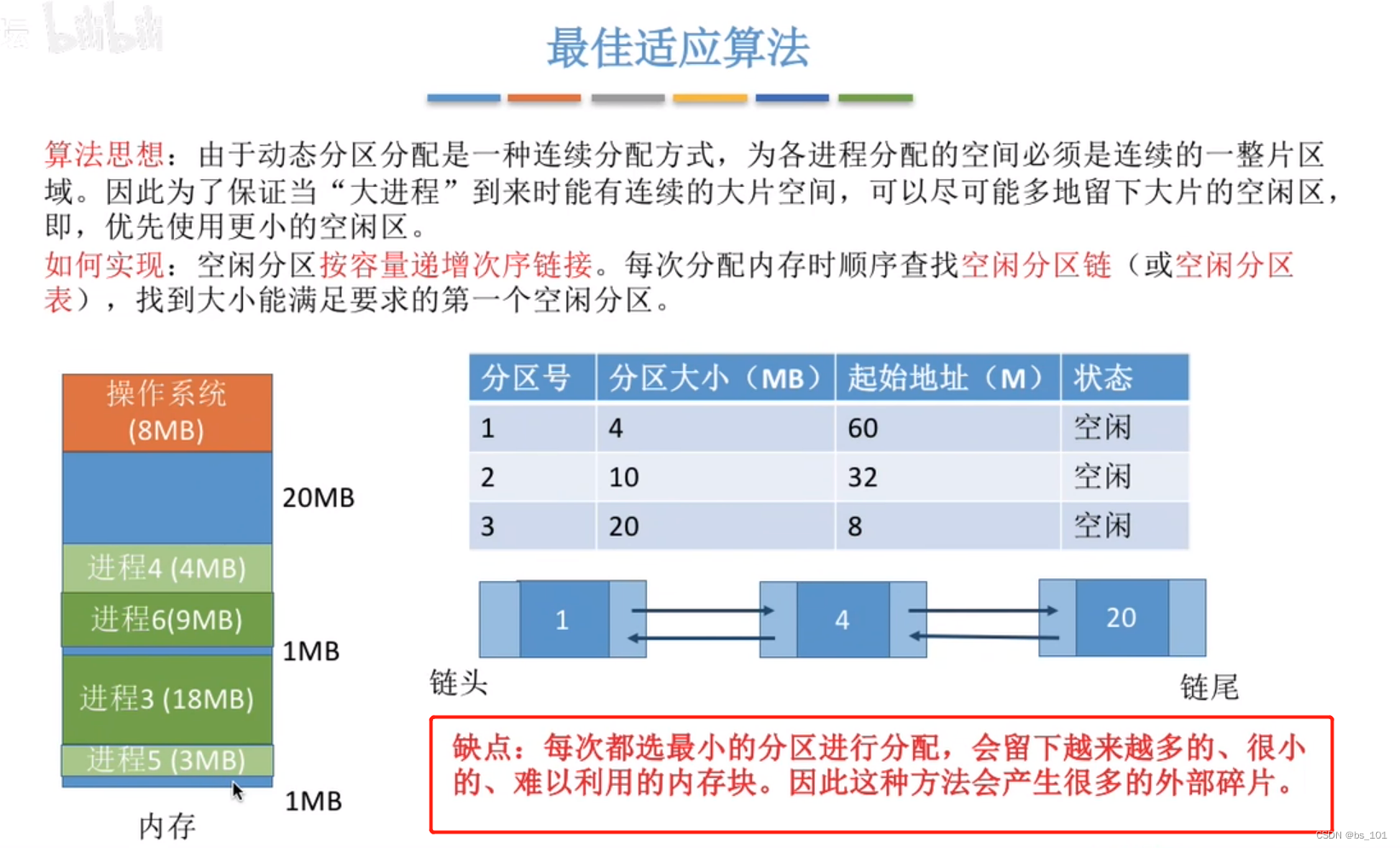
最佳适应算法
由于动态区分配是一种连续分配方式，为各进程分配的空间必须是连续的一整片区域。因此为了保证当“大进程”到来时有连续的大片空间，优先使用更小的空闲区
如何实现？
空闲分区以容量递增的次序排列。每次分配内存时顺序查找空闲分区链，找到大小能满足要求的第一个空闲分区
最坏适应算法
又称 最大适应算法
每次分配时优先使用最大的连续空闲区，这样分配后的剩余的空闲区就不会太小，方便使用
如何实现？
空闲分区按容量递减的次序排列。每次分配内存时顺序查找空闲分区链，找到大小能满足要求的第一个空闲分区
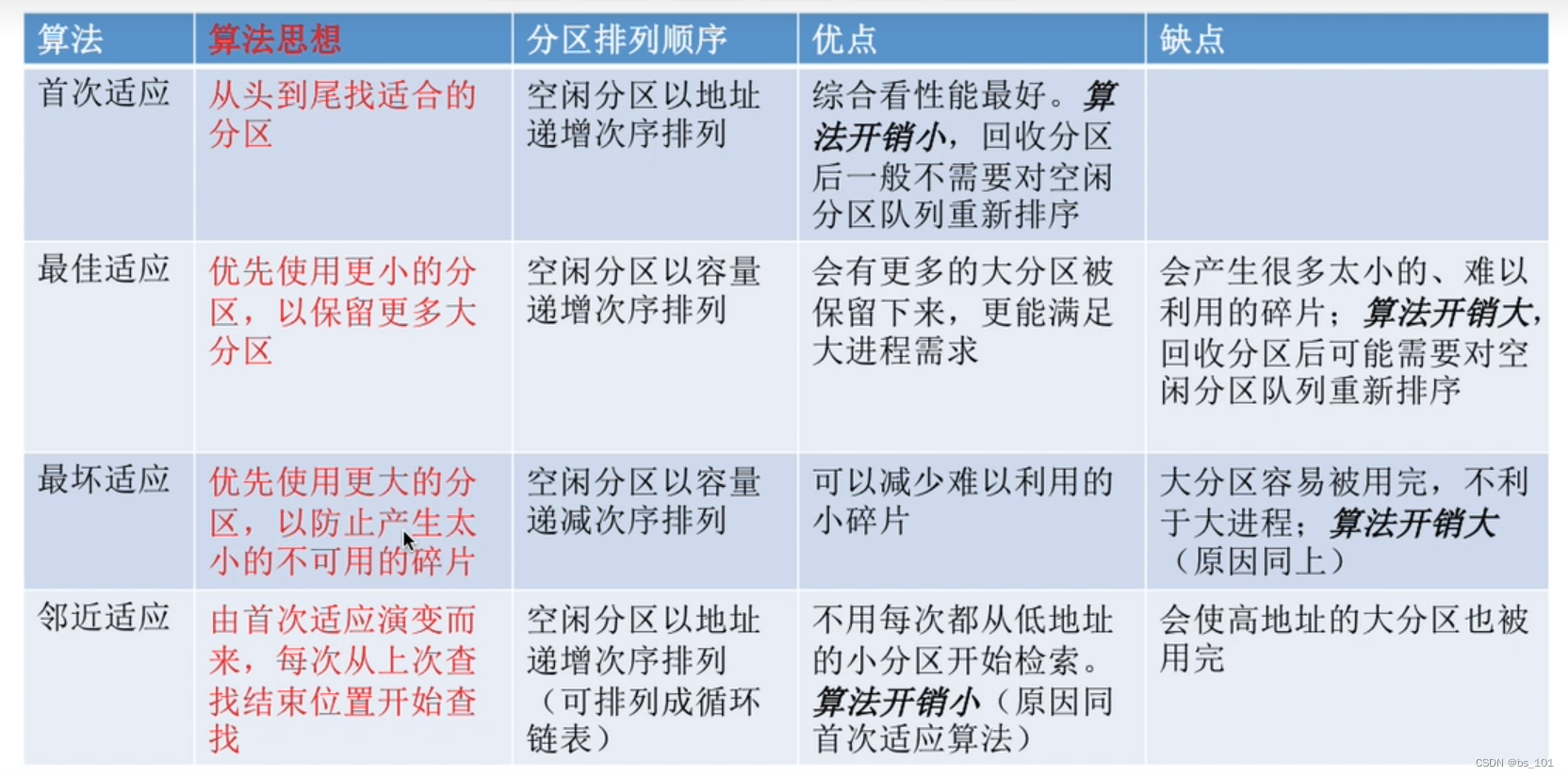
四种算法的优缺点
相关文章：
操作系统(day09) -- 连续分配管理方式
连续分配管理方式 单元连续分配 动态分区分配 1.系统要用什么样的数据结构记录内存的使用情况？ 两种常用的数据结构 空闲分区表 每个空闲分区对应一个表项。表项中包含分区号、分区大小、分区起始地址等信息空闲分区链 每个分区的起始部分和末尾部分分别设置前向…...
APISpace 带你一起走进西湖美景
俗话说：“上有天堂，下有苏杭”。 “欲把西湖比西子，浓妆艳抹总相宜” 今天我就带大家走进杭州的西湖美景。自古以来，文人歌者面对西湖美景留下千古绝句，还以西湖为背景书写了一段段动人的爱情传说。 天生自带浪漫色…...
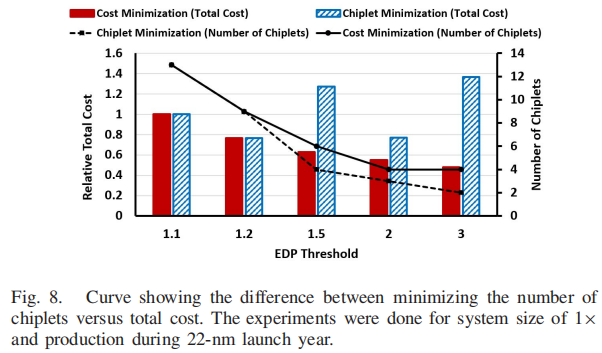
傻白探索Chiplet，Design Space Exploration for Chiplet-Assembly-Based Processors（十三）
阅读了Design Space Exploration for Chiplet-Assembly-Based Processors这篇论文，是关于chiplet设计空间探索的，个人感觉核心贡献有两个：1.提出使用整数线性规划算法进行Chiplet的选择；2.基于RE和NRE提出了一个cost模型ÿ…...
系统分析师真题2020试卷相关概念一
对象系统测试的基本概念： 面向对象系统的单元测试包括方法层次的测试、类层次的测试和类树层次的测试。方法层次的测试类似于传统软件测试中对单个函数的测试； 测试技术： 方法层次的测试，单个函数的测试；常用的技术：等价类划分测试、组合功能测试、递归函数的测试和多态…...
20230215_数据库过程_渠道业务计算过程
—20221209 渠道产能 —自有人员工号表 shzc.xc_qdcn_pgtx_opertype —select * from shzc.xc_qdcn_pgtx_opertype for update ; —渠道基础目录 shzc.xc_qdcn_pgtx_qdtype —select * from shzc.xc_qdcn_pgtx_qdtype for update ; SQL_STRING:‘update shzc.xc_qdcn_pgtx_q…...
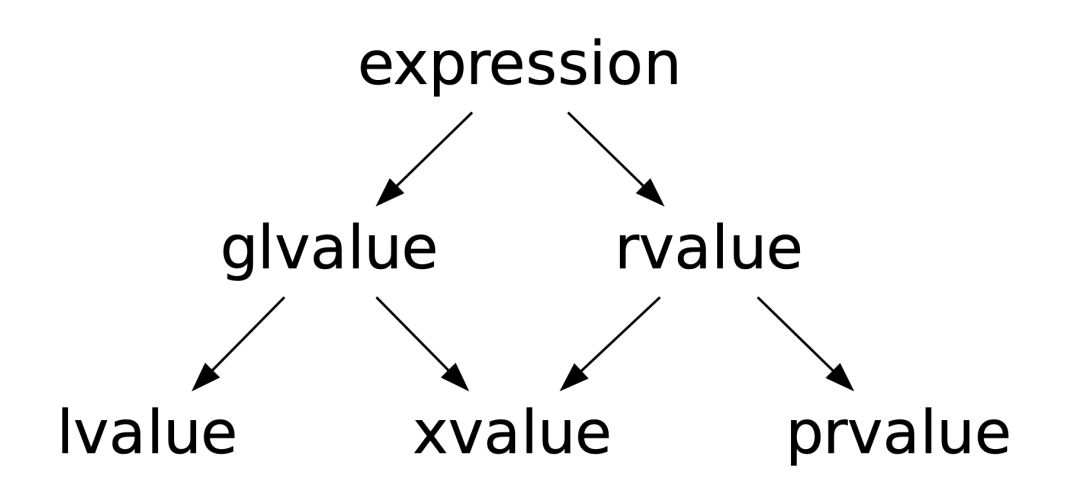
【C++】Expression的学习笔记
关于不同类别表达式的举例，请参考博文《C 中的值类别》 1. 左值和右值的简单理解 左值对应了具有内存地址的对象，而右值仅仅是临时使用的值对象。（引用自博文《C 中的值类别》）左值有名称（变量或常量名称）…...
[数据库迁移]-MySQL常见问题
[数据库迁移]-MySQL常见问题 森格 | 2023年2月 介绍：记录在MySQL数据库迁移过程中遇到的问题，以及解决方案。 文章目录[数据库迁移]-MySQL常见问题一、背景二、常见问题2.1 ERROR 20032.2 ERROR 12732.3 ERROR 10712.4 视图权限2.5 ERROR 1062三、总结一…...
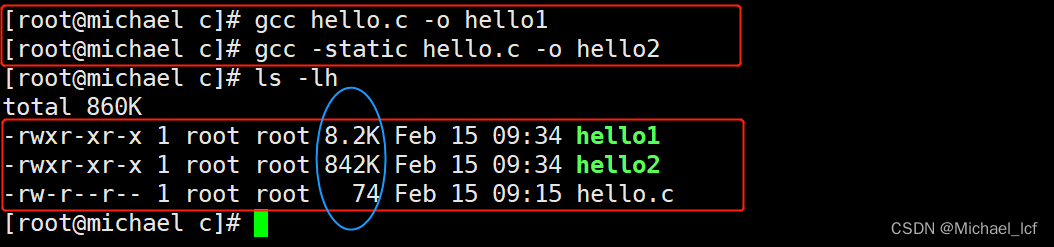
C语言编译过程
C语言编译过程1、C语言编译过程2、单c文件编译实践3、多c文件编译实践4、define4.1、不带参宏4.2、带参宏4.3、带参宏和带参函数的区别5、选择性编译ifdef、ifndef、if5.1、#ifdef5.2、#ifndef5.3、#if6、静态库和动态链接库6.1、静态库实践6.1.1、将mylib.c制作成静态库6.1.2、…...
前端学习 ---常用标签
常用标签 1,文本标签 文本标签是双标签，自带加粗效果，有自己对应的文本大小，并且独占一行，有默认间距 一级标签：< h1 > < /h1 > 二级标签：< h2 > < /h2> 三级标签：&l…...
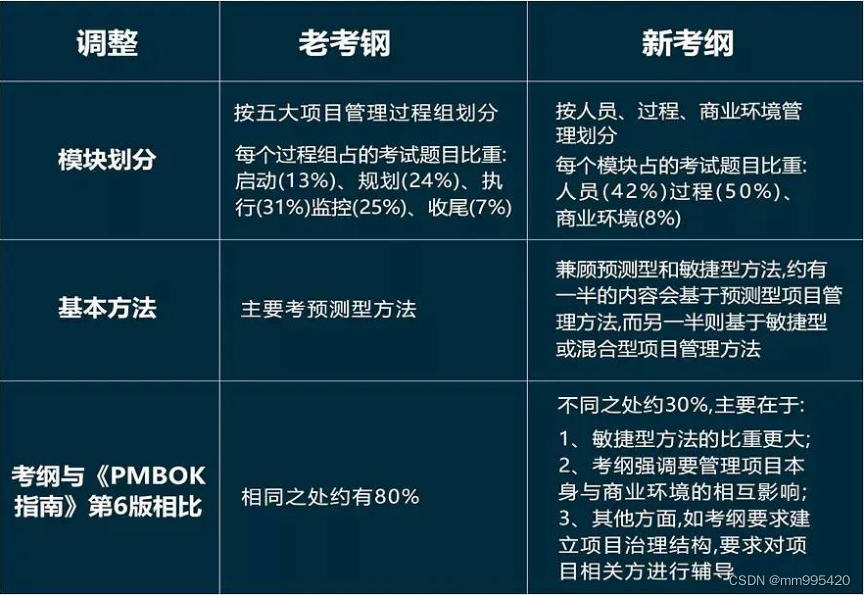
2023年PMP考试难不难？
整个考试的考察方向转向还是比较大的，基本上以“价值传递”和“以人为本”这两个出发点来考察项目经理所需要的能力。 1}新版提纲题目数量的变化 总题量从200道减少到180道，所以答题时间上相对变的宽裕一些。考试时间230分钟，中间有十分钟休…...
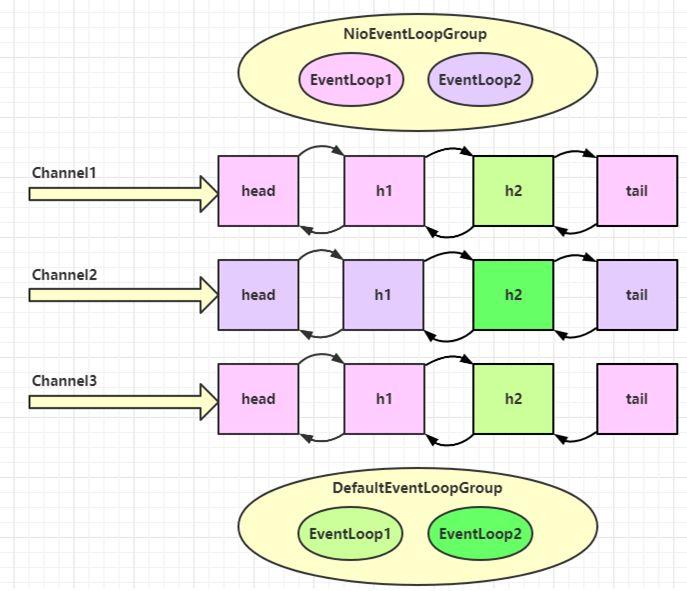
Netty 入门
文章目录一、概述1.1 Netty 是什么？1.2 Netty 的地位1.3 Netty 的优势二、Hello World2.1 目标2.2 服务器端2.3 客户端2.4 流程梳理三、组件3.1 EventLoop3.2 演示 NioEventLoop 处理 io 事件3.3 演示 NioEventLoop 处理普通任务3.4 演示 NioEventLoop 处理定时任务…...
收藏|一文掌握数据分析在企业的实际流程
一、数据分析概念 1.1 数据分析 是指用适当的统计分析方法对收集来的大量数据进行分析，将他们加以汇总和理解并消化，以求最大化地开发数据的功能，发挥数据的作用。 1.2 数据分析包括 描述性数据分析（初级数据分析）…...
100ask_imx6ull 输出PWM
查看PWM对应扩展板的引脚 100ask_imx6ul通过扩展板插槽来验证pwm波，所以这里通过扩展板的原理图及芯片手册可知，gpio4_io20，gpio4_io19分别对应着PWM8和PWM7。 设置设备树 打开官方NXP的工具i.MX pins v6工具，PWM7/PWM8的配置如…...
yolov5编译安卓APP：解决图像上全是检测框
yolov5编译安卓APP：解决图像上全是检测框前言一、第一个YOLOv5 APP1.参考链接2.详细说明3.APP检测时图像上全是框的解决方法二、第二个YOLOv5 APP1.参考链接2.详细说明3.APP检测时图像上全是框的解决方法三、其他1.APK打包2.修改APP图标与名字前言 YOLOv5编译安卓A…...
为什么我们需要地图？
想一想，武侠小说里面。一张藏宝图，引来江湖腥风血雨，要么是武功秘籍，要么是绝世宝剑，要么是富可敌国的财富，只要有了藏宝图，便可曲径通幽，到达彼岸。 由此可见，地图的重…...
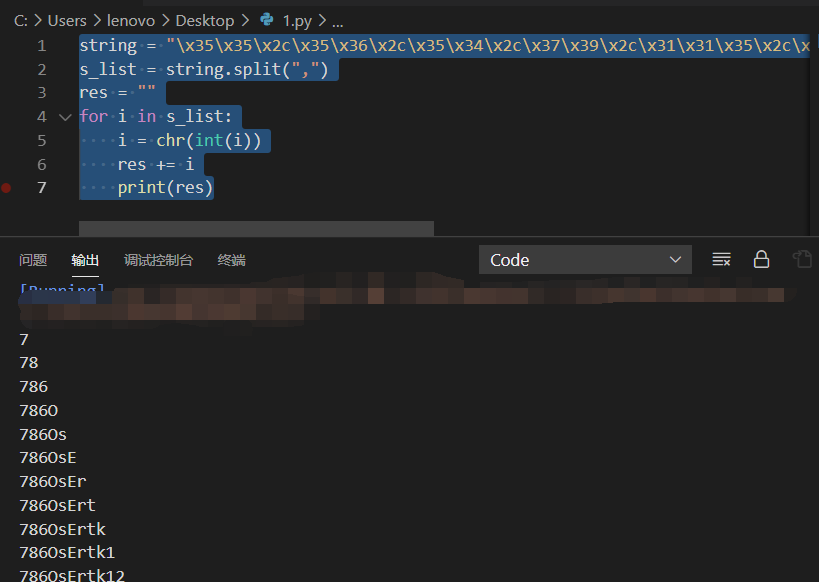
攻防世界1.新手练习区
4.攻防世界1.新手练习区 1.view_source 访问url： http://111.200.241.244:48855/ 鼠标点击右键不起作用，F12审查元素 得到flag为cyberpeace{0f3a3e4ab8c8664f3cf40d4240ec7b53} 2.robots 访问url： http://111.200.241.244:34362/ rob…...
Python进阶篇（二）-- Django 深入模型
上一节提到了Django是基于MVC架构的Web框架，MVC架构追求的是“模型”和“视图”的解耦合。所谓“模型”说得更直白一些就是数据（的表示），所以通常也被称作“数据模型”。在实际的项目中，数据模型通常通过数据库实现持久…...
ABAP SALV实现弹出ALV选择
问题场景 需要弹出一个ALV并获取选择的数据 实现思路 跳转屏幕弹出ALV（通过SALV）弹出ALV（通过REUSE_ALV_POPUP_TO_SELECT） 实现效果 因为这里需要的是单选，所以没有多选列 实现代码 MODULE sel_zfretype INPUT.…...
git check-pick，git patch 与 git stash 详解
大家好，我是 17。 今天和大家聊一聊 git check-pick，git patch 与 git stash 的用法。 git cherry-pick 为什么要用 cherry-pick? 不适合 merge 的场景就可以考虑 cherry-pick。 试想下面这些场景 只想同步分支的部分提交。两个分支是两上完全独立…...
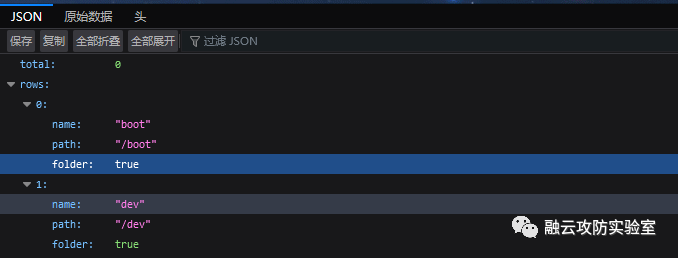
OA漏洞-到处搜集整理
一米OA getfile.jsp 任意文件读取漏洞 原文链接 漏洞复现 一米OA getfile.jsp 任意文件读取漏洞 一米OA协同办公系统,集成了OA办公自动化系统、手机客户端、专业报表工具,为全国千万企业用户提供全功能、性价比高的OA软件。一米OA getfile.jsp文件存在任意文件读取漏洞&am…...
eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明： 想象一下，你正在用eNSP搭建一个虚拟的网络世界，里面有虚拟的路由器、交换机、电脑（PC）等等。这些设备都在你的电脑里面“运行”，它们之间可以互相通信，就像一个封闭的小王国。 但是&#…...
DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽，大家好，我是左手python！ Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库，用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...
Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣（LeetCode） 思路： 笔者写过很多次这道题了，不想写题解了，大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...
关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径， 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解，但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后，通常在该文件中会出现以下配置&…...
如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要：设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP（Work-in-Progress）弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中，设立专门的紧急任务通道尤为重要，这能…...
基础测试工具使用经验
背景 vtune，perf, nsight system等基础测试工具，都是用过的，但是没有记录，都逐渐忘了。所以写这篇博客总结记录一下，只要以后发现新的用法，就记得来编辑补充一下 perf 比较基础的用法： 先改这…...
【2025年】解决Burpsuite抓不到https包的问题
环境：windows11 burpsuite:2025.5 在抓取https网站时，burpsuite抓取不到https数据包，只显示： 解决该问题只需如下三个步骤： 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件，或者在构建过程中仍然引用了旧的路…...
无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机（无人驾驶飞行器，UAV）技术的快速发展，其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统，无人机的“黑飞”&…...
在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）
考察一般的三次多项式，以r为参数： p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]； 此多项式的根为： 尽管看起来这个多项式是特殊的，其实一般的三次多项式都是可以通过线性变换化为这个形式…...