可数集和不可数集
有限集和无限集
后继集
设 S S S是任一集合,称 S + = S ∪ { S } S^+ = S\cup \left\{ S\right\} S+=S∪{S}为 S S S的后继集
自然数集
自然数集 N \mathbb{N} N的归纳定义是:
(1) ∅ ∈ N \empty \in \mathbb{N} ∅∈N
(2)若 n ∈ N n\in \mathbb{N} n∈N,则 n + ∈ N n^+ \in \mathbb{N} n+∈N
(3)若 S ∈ N S\in \mathbb{N} S∈N,且满足
1. ∅ ∈ S \empty \in S ∅∈S;
2. 若 n ∈ S n \in S n∈S,则 n + ∈ S n^+\in S n+∈S;
则 S = N S=\mathbb{N} S=N
我们约定,依次记
0 = ∅ 1 = 0 + = ∅ + = { ∅ } 2 = 1 + = { ∅ } + = { ∅ , { ∅ } } 3 = 2 + = { ∅ , { ∅ } } + = { ∅ , { ∅ } , { ∅ , { ∅ } } } ⋯ \begin{aligned} 0 &= \empty\\ 1 &= 0^+ = \empty^+ = \left\{\empty \right\}\\ 2 &= 1^+ = \left\{\empty \right\}^+ = \left\{ \empty, \left\{\empty \right\}\right\}\\ 3 &= 2^+ = \left\{ \empty, \left\{\empty \right\}\right\}^+=\left\{\empty, \left\{\empty \right\},\left\{ \empty, \left\{\empty \right\}\right\}\right\}\\ &\cdots \end{aligned} 0123=∅=0+=∅+={∅}=1+={∅}+={∅,{∅}}=2+={∅,{∅}}+={∅,{∅},{∅,{∅}}}⋯
由定义,每个自然数 n n n,都有 n ∈ n + n\in n^+ n∈n+和 n ⊆ n + n \subseteq n^+ n⊆n+,利用这一性质可在 N \mathbb{N} N上引进大小次序关系
若 m , n ∈ N m,n \in\mathbb{N} m,n∈N使 m ∈ n m\in n m∈n则称 m m m小于 n n n(或 n n n大于 m m m),记为 m < n m<n m<n(或 n > m n > m n>m)
我们将 N \mathbb{N} N的前 n n n个自然数的集合记为 N n = { 0 , 1 , 2 , ⋯ , n − 1 } \mathbb{N}_n = \left\{0, 1, 2,\cdots, n -1\right\} Nn={0,1,2,⋯,n−1}
设 A A A和 B B B使任意集合,若存在从 A A A到 B B B的双射,则称 A A A与 B B B是等势的,记为 A ∼ B A\sim B A∼B;
若 A A A与 B B B不等势,则记为 A ≁ B A\not\sim B A∼B
例子: N ∼ I \mathbb{N} \sim \mathbb{I} N∼I
作 f : N → I f:\mathbb{N} \to \mathbb{I} f:N→I,
f ( x ) = { − x + 1 2 , x is odd x 2 , o t h e r w i s e f\left(x\right) = \begin{cases} -\frac{x + 1}{2}, & \text{x is odd}\\ \frac{x}{2}, & otherwise \end{cases} f(x)={−2x+1,2x,x is oddotherwise
容易验证 f f f双射
若有 n ∈ N n\in \mathbb{N} n∈N,使得 N n ∼ A \mathbb{N}_n\sim A Nn∼A,则称 A A A是有限集,且称其基数为 n n n,记为 ∣ A ∣ = n \left|A\right|=n ∣A∣=n;
若 A A A不是有限集,则称 A A A是无限集
例子: 自然数是无限集合
证明:假设 N \mathbb{N} N是有限集,则有 n ∈ N n\in\mathbb{N} n∈N,使得存在双射
f : N n → N f:\mathbb{N}_n\to \mathbb{N} f:Nn→N
取 k = max { f ( i ) ∣ i ∈ N n } + 1 k = \max\left\{f\left(i\right)|i \in \mathbb{N}_n\right\} + 1 k=max{f(i)∣i∈Nn}+1
则 k ∈ N k\in\mathbb{N} k∈N,并且不存在 x ∈ N n x\in\mathbb{N}_n x∈Nn,使得 f ( x ) = k f\left(x\right) = k f(x)=k,即 f f f不是满射的,矛盾
定理1: 任何有限集都不能与它的真子集等势
定理2:
设 A A A是有限集, B B B是无限集, C C C是任意集合
(1)若 C ⊆ A C\subseteq A C⊆A,则 C C C是有限集
(2)若 B ⊆ C B\subseteq C B⊆C,则 C C C是无限集合
可数集与不可数集
设 A A A是任意集合。若 N ∼ A \mathbb{N}\sim A N∼A,则称 A A A是可数无限集,并称 A A A的基数为 ℵ 0 \aleph_0 ℵ0(阿列夫零),记为 ∣ A ∣ = ℵ 0 \left|A\right| = \aleph_0 ∣A∣=ℵ0
有限集和可数无限集称为可数集或可列集;非可数的集合称为不可数集
若 A A A是可数集,则存在双射 f : N n → A f: \mathbf{N}_n\to A f:Nn→A或者 f : N → A f:\mathbf{N}\to A f:N→A,因此 A A A中的元素可无重复排列为 f ( 0 ) , f ( 1 ) , ⋯ , f ( n − 1 ) f\left(0\right), f\left(1\right),\cdots, f\left(n-1\right) f(0),f(1),⋯,f(n−1)或者 f ( 0 ) , f ( 1 ) , f ( 2 ) , ⋯ f\left(0\right),f\left(1\right), f\left(2\right),\cdots f(0),f(1),f(2),⋯,反之,若 A A A中的元素能无重复地排列称 a 0 , a 1 , ⋯ , a n − 1 a_0, a_1,\cdots, a_{n-1} a0,a1,⋯,an−1或者 a 0 , a 1 , a 2 , ⋯ a_0,a_1,a_2,\cdots a0,a1,a2,⋯,则存在双射
f : N n → A , f ( i ) = a i f:\mathbb{N}_n\to A,\quad f\left(i\right) = a_i f:Nn→A,f(i)=ai
或者
f : N → A , f ( i ) = a i f:\mathbb{N}\to A,\quad f\left(i\right) =a_i f:N→A,f(i)=ai
由此可见, A A A是可数集当且仅当 A A A中所有元素可排列成一个无重复的序列,可以证明,“无重复”这一条件是可以省去的,也就是说,要证明一个集合是可数,只要证明该集合中的所有元素能够排成一个序列即可
例子1: N × N \mathbb{N}\times \mathbb{N} N×N是可数集
证明:
< 0 , 0 > < 0 , 1 > < 0 , 2 > ⋯ ↙ ↙ ↙ < 1 , 0 > < 1 , 1 > < 1 , 2 > ⋯ ↙ ↙ < 2 , 0 > < 2 , 1 > < 2 , 2 > ⋯ ↙ ⋮ ⋮ ⋮ \begin{array}{cccc} \left<0,0\right> & & \left<0,1\right> & & \left<0,2\right> & & \cdots\\ &\swarrow&&\swarrow&&\swarrow&\\ \left<1,0\right> & & \left<1,1\right> & & \left<1,2\right> & & \cdots\\ &\swarrow&&\swarrow&&&\\ \left<2,0\right> & & \left<2,1\right> & & \left<2,2\right> & & \cdots\\ &\swarrow&&&&&\\ \vdots & & \vdots & &\vdots & &\\ \end{array} ⟨0,0⟩⟨1,0⟩⟨2,0⟩⋮↙↙↙⟨0,1⟩⟨1,1⟩⟨2,1⟩⋮↙↙⟨0,2⟩⟨1,2⟩⟨2,2⟩⋮↙⋯⋯⋯
f : N × N → N f:\mathbb{N}\times \mathbb{N} \to \mathbb{N} f:N×N→N
f ( m , n ) = ( m + n ) ( m + n + 1 ) 2 + m f\left(m,n\right) = \frac{\left(m + n\right)\left(m +n + 1\right)}{2} + m f(m,n)=2(m+n)(m+n+1)+m
定理1: 可数集的任何子集都是可数集
定理2: 可数个可数集的并集是可数集
证明:
(1)有限个可数集的并集
设 A 0 , A 1 , ⋯ , A n − 1 A_0, A_1,\cdots, A_{n-1} A0,A1,⋯,An−1均是可数集,且 A i = { a i 0 , a i 1 , ⋯ , } , 0 ≤ i ≤ n − 1 A_i=\left\{a_{i0}, a_{i1},\cdots,\right\}, 0\le i \le n-1 Ai={ai0,ai1,⋯,},0≤i≤n−1
(若 A i A_i Ai是有限集,则重复 A i A_i Ai的重复 A i A_i Ai的最后一个元素)
令 ζ = { A 0 , A 1 , ⋯ , A n − 1 } \zeta = \left\{A_0, A_1,\cdots, A_{n-1}\right\} ζ={A0,A1,⋯,An−1},则 ∪ ζ \cup \zeta ∪ζ中的所有元素可排列为
A 0 a 00 a 01 a 02 ⋯ ↓ ↓ ↓ A 1 a 10 a 11 a 12 ⋯ ↓ ↓ ↓ ⋮ ⋮ ⋮ ⋮ ↓ ↓ ↓ A n − 1 a ( n − 1 ) 0 a ( n − 1 ) 1 a ( n − 1 ) 2 ⋯ \begin{array}{cccc} A_0 & a_{00} & a_{01}& a_{02}&\cdots\\ &\downarrow & \downarrow&\downarrow&\\ A_1 & a_{10} & a_{11}& a_{12}&\cdots\\ &\downarrow & \downarrow&\downarrow&\\ \vdots & \vdots & \vdots & \vdots &\\ &\downarrow & \downarrow&\downarrow&\\ A_{n-1} & a_{\left(n-1\right)0} & a_{\left(n-1\right)1}& a_{\left(n-1\right)2}&\cdots\\ \end{array} A0A1⋮An−1a00↓a10↓⋮↓a(n−1)0a01↓a11↓⋮↓a(n−1)1a02↓a12↓⋮↓a(n−1)2⋯⋯⋯
按上面箭头所指的方向,可将 ∪ ζ \cup \zeta ∪ζ中的所有元素排列成一个序列,故 ∪ ζ \cup \zeta ∪ζ是可数集
(2)可数无限个可数集的并集(?)
设 A 0 , A 1 , ⋯ A_0, A_1,\cdots A0,A1,⋯军事可数集,且 A i = { a i 0 , a i 1 , ⋯ , } , i ∈ N A_i=\left\{a_{i0}, a_{i1},\cdots,\right\}, i\in\mathbb{N} Ai={ai0,ai1,⋯,},i∈N
(若 A i A_i Ai是有限集,则重复 A i A_i Ai的重复 A i A_i Ai的最后一个元素)
令 ζ = { A 0 , A 1 , ⋯ } \zeta = \left\{A_0, A_1,\cdots\right\} ζ={A0,A1,⋯},则 ∪ ζ \cup \zeta ∪ζ中的所有元素可排列为
A 0 a 00 a 01 a 02 ⋯ ↙ ↙ ↙ A 1 a 10 a 11 a 12 ⋯ ↙ ↙ A 2 a 20 a 21 a 22 ⋯ ↙ ⋮ ⋮ ⋮ ⋮ \begin{array}{cccc} A_0 & a_{00}&&a_{01}&&a_{02}&&\cdots\\ &&\swarrow&&\swarrow&&\swarrow&\\ A_1 & a_{10}&&a_{11}&&a_{12}&&\cdots\\ &&\swarrow&&\swarrow&&&\\ A_2 & a_{20}&&a_{21}&&a_{22}&&\cdots\\ &&\swarrow&&&&&\\ \vdots & \vdots&&\vdots&&\vdots&&\\ \end{array} A0A1A2⋮a00a10a20⋮↙↙↙a01a11a21⋮↙↙a02a12a22⋮↙⋯⋯⋯
按上面所示的方式,可将 ∪ ζ \cup\zeta ∪ζ的所有元素排成一个序列,故 ∪ ζ \cup\zeta ∪ζ是可数的
定理3 若 A A A和 B B B是可数集,则 A × B A\times B A×B是可数集
证明:因为 A A A和 B B B是可数集,不妨设 A = { a 0 , a 1 , ⋯ } A = \left\{a_0,a_1,\cdots\right\} A={a0,a1,⋯}和 B = { b 0 , b 1 , ⋯ } B = \left\{b_0,b_1,\cdots\right\} B={b0,b1,⋯}
(若是有限集则重复最后一个元素,那么 A × B A\times B A×B中所有元素可排列为)
< a 0 , b 0 > < a 0 , b 1 > < a 0 , b 2 > ⋯ ↙ ↙ ↙ < a 1 , b 0 > < a 1 , b 1 > < a 1 , b 2 > ⋯ ↙ ↙ < a 2 , b 0 > < a 2 , b 1 > < a 2 , b 2 > ⋯ ↙ ⋮ ⋮ ⋮ \begin{array}{cccc} \left<a_0,b_0\right> & & \left<a_0,b_1\right> & & \left<a_0,b_2\right> & & \cdots\\ &\swarrow&&\swarrow&&\swarrow&\\ \left<a_1,b_0\right> & & \left<a_1,b_1\right> & & \left<a_1,b_2\right> & & \cdots\\ &\swarrow&&\swarrow&&&\\ \left<a_2,b_0\right> & & \left<a_2,b_1\right> & & \left<a_2,b_2\right> & & \cdots\\ &\swarrow&&&&&\\ \vdots & & \vdots & &\vdots & &\\ \end{array} ⟨a0,b0⟩⟨a1,b0⟩⟨a2,b0⟩⋮↙↙↙⟨a0,b1⟩⟨a1,b1⟩⟨a2,b1⟩⋮↙↙⟨a0,b2⟩⟨a1,b2⟩⟨a2,b2⟩⋮↙⋯⋯⋯
按上面的方式,可将 A × B A\times B A×B的所有元素排列成一个序列,故 A × B A\times B A×B是可数的
同理可证若 A A A是可数集,则 A n A^n An也是可数集
定理4: 实数集合的子集 [ 0 , 1 ] \left[0,1\right] [0,1]不是可数无限集合
证明:设 f : N → [ 0 , 1 ] f:\mathbb{N}\to \left[0,1\right] f:N→[0,1]我们把 f f f的值顺序排列为十进制小数:
f ( 0 ) = 0. x 00 x 01 x 02 ⋯ , f ( 1 ) = 0. x 10 x 11 x 12 ⋯ , ⋯ \begin{aligned} f\left(0\right) &= 0.x_{00}x_{01}x_{02}\cdots,\\ f\left(1\right) &= 0.x_{10}x_{11}x_{12}\cdots,\\ \cdots \end{aligned} f(0)f(1)⋯=0.x00x01x02⋯,=0.x10x11x12⋯,
其中 0 ≤ x i j ≤ 9 ( i , j ∈ N ) 0\le x_{ij} \le 9\left(i,j\in\mathbb{N}\right) 0≤xij≤9(i,j∈N)
构造 y = 0. y 0 y 1 y 2 ⋯ y=0.y_0y_1y_2\cdots y=0.y0y1y2⋯
y i = { 1 , x i i ≠ 1 2 , x i i = 1 y_i=\begin{cases} 1, &x_{ii}\neq 1\\ 2,&x_{ii} = 1 \end{cases} yi={1,2,xii=1xii=1
y ∈ [ 0 , 1 ] y\in\left[0,1\right] y∈[0,1]但是 y ∉ f ( N ) y\notin f\left(\mathbb{N}\right) y∈/f(N)
f f f不满射
这个方法叫康托对角线法
{ 0 , 1 1 , 1 2 , 1 3 , ⋯ } ⊆ [ 0 , 1 ] \left\{0, \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \cdots\right\} \subseteq \left[0,1\right] {0,11,21,31,⋯}⊆[0,1]可见不是有限集
设 A A A是任意集合,若 [ 0 , 1 ] ∼ A \left[0,1\right]\sim A [0,1]∼A,则称 A A A的基数为 ℵ \aleph ℵ,并称 A A A是具有连续统势的集合,记为 ∣ A ∣ = ℵ \left|A\right|=\aleph ∣A∣=ℵ
定理5 设 A , B , C A, B, C A,B,C和 D D D是任意集合, A ∼ B , C ∼ D , A ∩ C = B ∩ D = ∅ A\sim B, C \sim D, A\cap C = B \cap D = \empty A∼B,C∼D,A∩C=B∩D=∅,则 A ∪ C ∼ B ∪ D A\cup C \sim B\cup D A∪C∼B∪D
证明:由于 A ∼ B , C ∼ D A\sim B, C\sim D A∼B,C∼D,存在双射 f 1 : A → B f_1:A\to B f1:A→B和 f 2 : C → D f_2: C\to D f2:C→D
令
f : A ∪ C → B ∪ D f ( x ) = { f 1 ( x ) , x ∈ A f 2 ( x ) , x ∈ C f:A \cup C \to B \cup D\\ f\left(x\right) = \begin{cases} f_1\left(x\right), & x \in A\\ f_2\left(x\right), & x \in C\\ \end{cases} f:A∪C→B∪Df(x)={f1(x),f2(x),x∈Ax∈C
因为 A ∩ C = ∅ A\cap C = \empty A∩C=∅,所以 f f f是一个函数,下面证明 f f f双射
(1)f是满射,对任意的 y ∈ B ∪ D y\in B \cup D y∈B∪D,则有 y ∈ B ∨ y ∈ D y \in B \vee y \in D y∈B∨y∈D
若 y ∈ B y \in B y∈B,因为 f 1 f_1 f1满射,所以有 x ∈ A x\in A x∈A使 y = f 1 ( x ) y = f_1\left(x\right) y=f1(x),即 x ∈ A ∪ C x\in A \cup C x∈A∪C,使 y = f 1 ( x ) = f ( x ) y= f_1\left(x\right) = f\left(x\right) y=f1(x)=f(x)
若 y ∈ D y\in D y∈D,同理
故 f f f满射
(2)f单射。对任意的 x 1 , x 2 ∈ A ∪ C x_1,x_2\in A\cup C x1,x2∈A∪C,若 f ( x 1 ) = f ( x 2 ) f\left(x_1\right) = f\left(x_2\right) f(x1)=f(x2),那么
若 f ( x 1 ) = f ( x 2 ) ∈ B f\left(x_1\right) = f\left(x_2\right) \in B f(x1)=f(x2)∈B,则因为 f ( A ) = B , f ( C ) = D , B ∩ D = ∅ f\left(A\right) = B,f\left(C\right)=D,B\cap D = \empty f(A)=B,f(C)=D,B∩D=∅, 有 x 1 , x 2 ∈ A x_1,x_2\in A x1,x2∈A
所以 f ( x 1 ) = f 1 ( x 1 ) , f ( x 2 ) = f 1 ( x 2 ) f\left(x_1\right) =f_1\left(x_1\right),f\left(x_2\right) =f_1\left(x_2\right) f(x1)=f1(x1),f(x2)=f1(x2),即 f 1 ( x 1 ) = f 1 ( x 2 ) f_1\left(x_1\right) =f_1\left(x_2\right) f1(x1)=f1(x2)
又因为 f 1 f_1 f1单射, x 1 = x 2 x_1=x_2 x1=x2
若 f ( x 1 ) = f ( x 2 ) ∈ D f\left(x_1\right)=f\left(x_2\right)\in D f(x1)=f(x2)∈D,同理可证 x 1 = x 2 x_1=x_2 x1=x2
f f f单射
所以 A ∪ C ∼ B ∪ D A\cup C \sim B \cup D A∪C∼B∪D
相关文章:

可数集和不可数集
有限集和无限集 后继集 设 S S S是任一集合,称 S S ∪ { S } S^ S\cup \left\{ S\right\} SS∪{S}为 S S S的后继集 自然数集 自然数集 N \mathbb{N} N的归纳定义是: (1) ∅ ∈ N \empty \in \mathbb{N} ∅∈N (…...
》)
<Linux>《Linux 之 ps 命令详解大全(含实用命令)》
《Linux 之 ps 命令详解大全(含实用命令)》 1 常用命令1.1 显示所有当前进程1.2 显示所有当前进程1.3 显示所有当前进程1.4 根据用户过滤进程1.5 根据 CPU 使用来升序排序1.6 根据用户过滤进程1.7 查询全10个使用cpu和内存最高的应用1.8 通过进程名和PID…...

华为OD机试真题 Java 实现【寻找关键钥匙】【2023Q1 100分】
一、题目描述 小强正在参加《密室逃生》游戏,当前关卡要求找到符合给定 密码K(升序的不重复小写字母组成)的箱子,并给出箱子编号,箱子编号为1~N。 每个箱子中都有一个字符串s,字符串由大写字母,小写字母,数字,标点符号,空格组成,需要在这些字符串中找出所有的字母…...
)
项目中遇到的一些问题总结(十三)
extension-configs 和 shared-configs 的区别 在 Nacos 配置管理中,extension-configs 和 shared-configs 分别是两种不同类型的配置,它们的主要区别在于它们的使用场景和作用。 extension-configs 是一种应用程序向 Nacos 注册的扩展配置。它主要用于给…...
)
药品存销信息管理系统数据设计与实现(包括需求分析,数据库设计,数据表、视图、存储过程等)
前言 可前往链接直接下载: https://download.csdn.net/download/c1007857613/87776664 或者阅读本博文的详细介绍,本博文也包含所有详细内容。 一、需求分析 a.“药品存销信息管理系统”只是对数据库应用技术的一个样本数据库的实例,重在对数据库一些方法的熟悉与掌握,…...
PyTorch-Loss Function and BP
目录 1. Loss Function 1.1 L1Loss 1.2 MSELoss 1.3 CrossEntropyLoss 2. 交叉熵与神经网络模型的结合 2.1 反向传播 1. Loss Function 目的: a. 计算预测值与真实值之间的差距; b. 可通过此条件,进行反向传播。 1.1 L1Loss import torch from …...

centos docker安装mysql8
1、创建挂载文件夹 mkdir -p /mydata/mysql/log mkdir -p /mydata/mysql/data mkdir -p /mydata/mysql/conf 2、拉取镜像最新版本,如果写 mysql:8.0.26可以指定版本 docker pull mysql 3、启动命令 docker run -p 3306:3306 --restartalways -v /mydata/mysql/log:…...
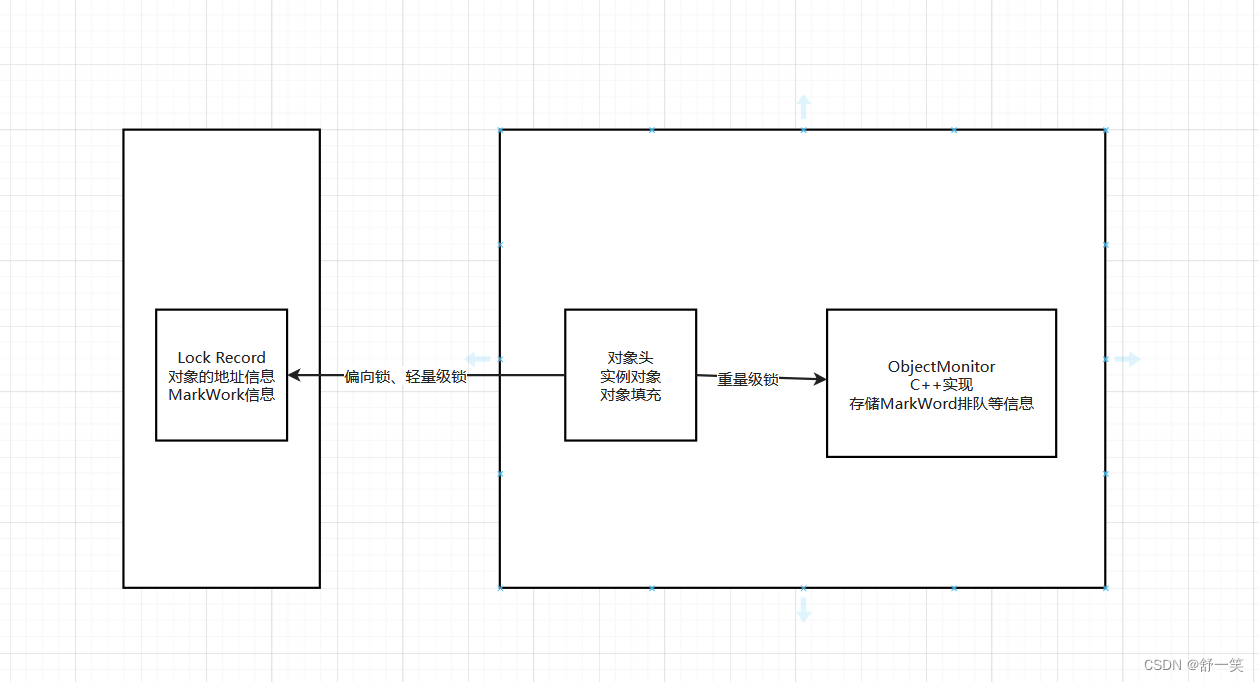
Java中synchronized锁的深入理解
使用范围 synchronized使用上用于同步方法或者同步代码块在锁实现上是基于对象去实现使用中用于对static修饰的便是class类锁使用中用于对非static修饰的便是当前对象锁 synchronized的优化 在jdk1.6中对synchronized做了相关的优化 锁消除 在synchronized修饰的代码块中…...

Find My资讯|iOS17将重点改进钱包、Find My、SharePlay和AirPlay等功能
彭博社的马克・古尔曼(Mark Gurman)在最新一期 Power On 时事通讯中表示,苹果即将推出的 iOS 17 系统将改进 Wallet、Find My、SharePlay 和 AirPlay 等多项功能。 古尔曼在博文中还表示苹果会增强 Find My 的位置服务,同样也没…...

什么是webSocket?
什么是webSocket WebSockets是一种协议,它允许在Web应用程序中建立持久连接。这意味着当客户端与服务器建立连接后,它们可以始终保持连接状态,直到其中一个终止连接。相比于传统的HTTP协议,WebSockets提供了更高效的方式来处理实…...

黑马Redis视频教程高级篇(一:分布式缓存)
目录 分布式缓存 一、Redis持久化 1.1、RDB持久化 1.1.1、执行时机 1.1.2、RDB原理 1.1.3、小结 1.2、OF持久化 1.2.1、AOF原理 1.2.2、OF配置 1.2.3、AOF文件重写 1.3、RDB与AOF对比 二、Redis主从 2.1、搭建主从架构 2.1.1、集群结构 2.1.2、准备实例和配置 …...
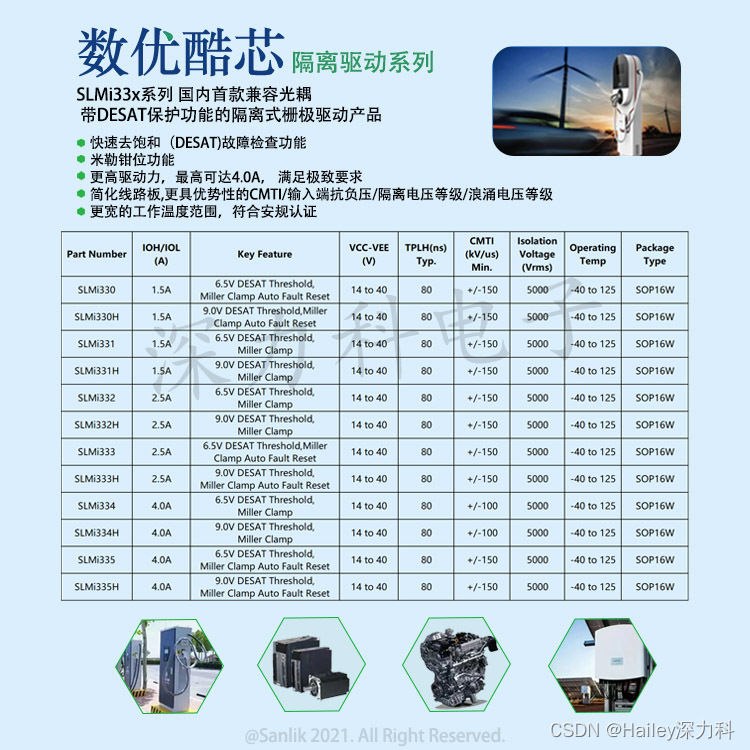
SLMi331数明深力科带DESAT保护功能隔离驱动应用笔记
SLMi33X系列SLMi331数明深力科首款单通道带DESAT保护功能的IGBT/SiC隔离驱动器。内置快速去饱和(DESAT) 故障检测功能、米勒钳位功能、漏极开路故障反馈、软关断功能以及可选择的自恢复模式,兼容光耦隔离驱动器。 SLMi331的DESAT阈值为6.5V,其最大驱动电…...

【嵌入式Linux基础】启动初始化程序--init程序
文章目录 内核启动后初始化程序简介BusyBox initBuildroot init 脚本 后记 内核启动后 内核引导代码在initramfs中通过内核命令行中的root指定的文件系统中去寻找根系统文件,并执行一个相应的程序。在默认情况下,对于initramfs这个程序是/init࿰…...

基于Java实现农产品交易平台的设计与实现_kaic
【摘要】农业是我国国民经济的重要组成部分,随着信息化的普及,4G网络、光纤以及5G网络也日益完善,农业信息化的发展成为了必然。同时,由于本年疫情原因,导致农作物积压销售,甚至腐烂造成不必要的浪费&#…...
视频转换、视频压缩、录屏等工具合集:迅捷视频工具箱
这是一款功能强大的视频处理软件,提供了多种视频处理功能。可以使用该软件进行视频剪辑、视频转换、音频转换、视频录像、视频压缩、字幕贴图等多种操作。软件界面简洁易用,操作方便,可以满足各种视频处理需求。 基本功能 视频压缩ÿ…...

理解时序数据库的时间线
在当今数据爆炸的时代,时序数据已经成为企业和组织中不可或缺的一部分。它们包括了从传感器、监控设备、日志记录系统和金融交易等多种来源的大量数据,这些数据按照时间顺序排列,记录了各种事件和活动的发生和变化。时序数据的分析和处理对于…...

音视频技术开发周刊 | 295
每周一期,纵览音视频技术领域的干货。 新闻投稿:contributelivevideostack.com。 微软炸通Windows与ChatGPT全家桶!人手一个Copilot,AI宇宙降临 三位OpenAI掌舵人亲自撰文:我们应该如何治理超级智能? OpenA…...
15稳压二级管
目录 一、基本原理 二、I-V特性 三、工作原理 四、参数 1、Vz 2、Zzt和Zzk 3、IrVr 4、VfIf 5、Pd 五、应用 1、示例1 2、串联应用 3、钳位电路 六、动态电阻 一、基本原理 稳压二极管或“击穿二极管”(有时也称为齐纳二极管)基本上与标准PN结二极管相同…...
一些零零碎碎的记录
Questions1. 用户访问多网址服务器同一个IP是怎么回事 Q:用户访问服务器的同一个IP不同网址,服务器是如何区分的A: 在 HTTP 协议中,客户端通过发送请求报文来向服务器请求资源。每个 HTTP 请求都包含一个 HTTP 头部,其中包括了一些关键信息&…...

MyBatis - Spring Boot 集成 MyBatis
文章目录 1.版本要求2.导入依赖3.自动配置2.可配置项 MyBatis-Spring-Boot-Starter 可以帮助你更快地在 Spring Boot 之上构建 MyBatis 应用。通过使用该模块我们能够快速实现以下目的: 构建单体应用程序将几乎不需要样板配置使用更少的 XML 配置 1.版本要求 MyB…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
